一种基于单站的飞机起飞空间位置测量方法

刘晓磊，张兴国，陈 贝

(中国飞行试验研究院，西安 710089)

0 引言

飞机起飞着陆是新机试飞中最重要的环节之一。飞机起飞前的偏心量、飞机离地速度以及飞机起飞时的轨迹等参数测量是新机鉴定定型不可或缺的课题。目前针对该课题，国内外提出了一些常用的测量手段，武瑞娟等提出一种利用光电经纬仪等大型测量设备进行飞机轨迹的测量方法，该方法利用光电经纬仪连续跟踪飞机起飞整个过程，利用系统内部的方位角、俯仰角、测距仪等分系统联合工作来测取飞机的三维运动轨迹，该方法的主要缺陷是设备测量范围小，测量精度在半米左右，容易受到天气影响，设备造价昂贵。李东等提出一种GPS测量导弹轨迹的方法，该方法利用机载GPS与导弹上的GPS进行实时差分，解算出目标相对于载机的相对位置、速度等信息，该测量方法相对简单，但是该方法测量精度在0.5～1 m，采样率一般在25帧/s左右。冯巧宁等提出一种基于多台高速相机联合交会的飞机着陆轨迹姿态测量方法，该方法通过对多台相机进行相机标定，然后通过两台或者多台相机进行前方交会实现飞机轨迹的测量，该方法利用高速相机进行高频率的影像采集，较基于GPS的轨迹测量其采样率提升4倍以上，测得的轨迹点更加密集，利于事后试飞架次的参数分析。但是由于高速相机造价昂贵，该测量阵系统需要6～8台高速相机同时进行保障，导致其成本增加，且整个系统的每台相机时间要严格对应，否则无法交会测量，影响测量精度。

为了降低试飞成本以及进一步提升试飞测量精度及工作效率，文中根据某型飞机性能鉴定试飞科目的具体需求，提出一种基于单站高速相机的飞机起飞关键参数测量方法，用于测量飞机起飞前精确空间三维坐标，进而可获取飞机在不同工况下的起飞偏心量，滑跑速度等参数，为飞机起落架等性能提供重要鉴定依据。以摄影测量共线方程为基础，引入飞行过程中的相对不变量，从而实现单站相机的解算，将相机成本减少一半，工作效率提升一倍，经飞行试验验证提出的单站测量的方法解算结果满足测量任务的精度要求。

1 系统布设

根据某型飞机性能鉴定试飞需求，需测量飞机起飞过程精确三维空间坐标，测量范围不小于200 m，测量频率不低于200 Hz，测量精度需保证在5 cm以上，且测量设备需架设在离跑道中轴线35 m以外。由于飞机在滑跑过程中加速度过大，利用传统的GPS测量方式很难得到高频率数据，且精度难以满足测量要求，因此构建了一套基于单站测量的摄影测量系统，该套系统主要由高速影像采集系统、数据传输系统、数据转换系统、数据交换系统以及数据处理系统组成，其整体系统布局图如图1所示。

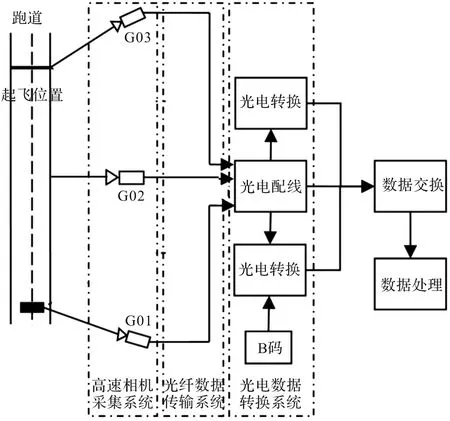
图1 整体系统布局图

其中高速相机采集系统由3台AOS高速相机(帧率500 Hz)G01～G03构成，每台相机距离跑道中轴线42 m，相机视场角80°，单台相机测量范围70 m，相邻相机间距70 m，故可拼接测量飞机滑跑中后段210 m范围轨迹，满足测试需求。经200余架次的飞行试验，系统故障率在1%以下，充分保证了飞行试验的安全。

2 前方交会原理

传统的摄影测量方法是通过多台相机对视场范围内的物体进行三维坐标解算，即通过不同相机获取同一时刻的影像再提取不同影像中的同名点坐标，形成共线方程组：

(1)

其中：=coscos-sinsinsin;=-cos·sin-sinsincos；=-sincos；=cossin；=coscos；=-sin；=sincos+cos·sinsin；=-sinsin+cossincos；=coscos；,,为外方位线元素；,,为外方位角元素；(，)为像主点坐标；为相主距，均可通过相机标定获得。

由式(1)可知每个像点可列两个方程，因此欲求解3个未知数至少需要两个同名像点坐标方可解算该点物方空间坐标。其优势是解算精度相对较高，但是解算过程相对复杂需要多台相机将时间严格统一，需要相同的授时源，且解算过程复杂，万一其中某台相机出现故障将无法得出物方点坐标。

3 单站测量原理

为进一步节约试飞成本以及提升数据处理效率，提出一种基于单站的测量方法，即每个站点仅需布设一台相机便可实现该台相机视场范围内运动目标空间位置的精确测量，不再需要多台相机进行公共区域同名目标交会。其主要思路是在传统摄影测量共线方程的基础上，引入机体中轴线上两个刚性不动标志点，同时结合飞机惯导姿态信息对共线方程(式(1))进行约束，从而实现单台高速相机对飞机滑行阶段轨迹的高精度测量。其测量原理如图2所示。

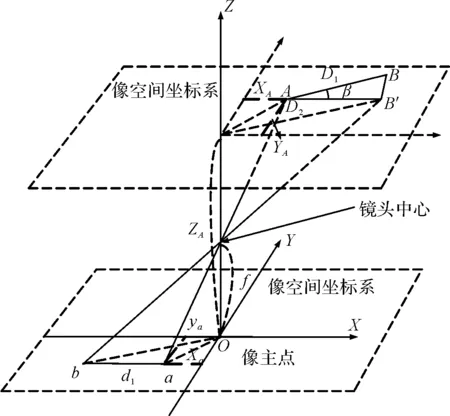
图2 单站测量原理图

通过内参标定，将相机成像模型转化为标准针孔成像模式，根据针孔共轭三角成像原理可知，当一个刚性长度物体在与像平面平行的空间平面运动时，其在相机中的成像与真实物体具有相似三角形关系。

设飞机中轴线两标志点，之间的空间距离(视为刚体)为(该距离可由全站仪进行测量获得)，通过飞机惯导数据可以得到飞机中轴线与跑道坐标系0平面之间的夹角，根据第2节得到的相机外参可知像平面与跑道坐标系面的夹角为，因此可得刚体与像平面夹角=+，故其在像平面上的投影长度=cos，根据相机内参可获取，之间畸变矫正之后的像点距离，由相似关系可得：

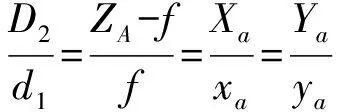
(2)

其中：(,)为像点畸变矫正后的像点坐标，可由相机内参计算而来；(，，)为物点在像片空间坐标系下的三维坐标。

由式(2)可得物点在像空间坐标系下的三维坐标为：

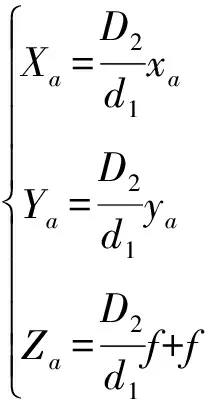
(3)

得到像空间坐标系下坐标后由第4节得到的相机标定外参(相机像空间坐标系与跑道坐标系之间的位置姿态关系)可将(，，)转化至最终跑道坐标系(，，)，具体转化关系为：

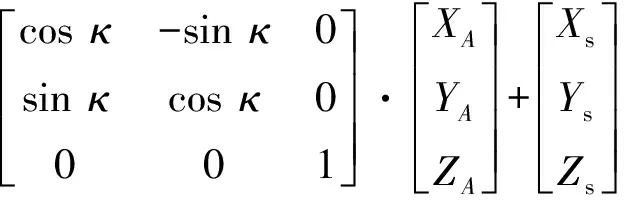
(4)

4 相机标定

为了利用相机获取飞机高精度三维坐标，必须建立相机成像的几何模型，需要对相机进行标定解算，确定跑道坐标系下控制点三维几何位置与其在图像中对应点之间的相互关系。标定过程分为内参标定和外参标定两部分，内参标定利用棋盘格标定算法进行标定，包括像主点坐标、像主距以及相机畸变系数，其核心思想是从不同方位对棋盘格进行拍摄，通过提取影像中每一棋盘格角点从而建立起与标定板上特征点的对应关系，通过每幅影像的单应矩阵实现相机的标定。其原理公式为：

(5)

内参数标定好之后即可将相机固定在机场预设位置，调整好视场角之后，建立跑道坐标系，同时用全站仪测量相机初始位置(作为最小二乘算法迭代的初值)，因为机场跑道较长，通过滑动交替异步式移动测量标志单元(由3组不同空间位置的标志牌构成)的方式建立物方标定场，即测量标志单元每到达一个预设位置，全站仪精确测量每个标志牌十字中心的三维坐标，同时相机对其进行拍摄，构建起标志牌的物方坐标与像点坐标的一一对应关系。接着利用后方交会原理完成不同相机在同一跑道坐标系下的外方位元素(包括外方位线元素,,和外方位角元素,,)标定。机场坐标系建立以及测量标识单元轨迹如图3所示。

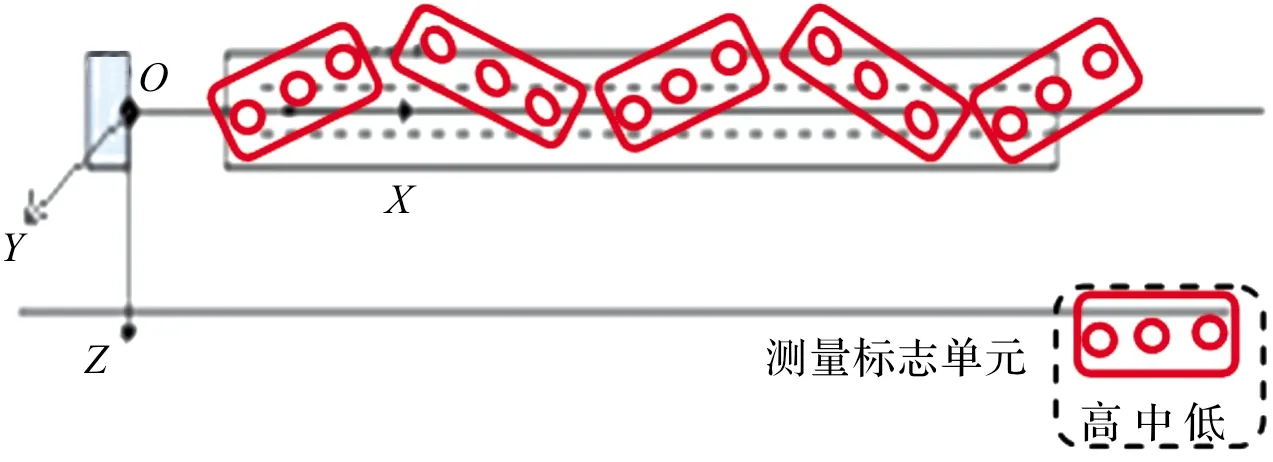
图3 机场坐标系建立以及测量标志单元轨迹示意图

根据相机成像原理，通过共线方程可建立像点与物点的对应关系，如式(6)所示：

(6)

将式(6)看成外方位元素的函数时，其是非线性的。将像点坐标视为观测值，将式(6)线性化并展开可得误差方程的矩阵形式为：

(7)

其中()，()为未知数的近似值代入式(6)所计算出的影像坐标。

(8)

(9)

其中=-。

若已知个控制点，可列出2个方程式，写成总误差方程为：

=-

(10)

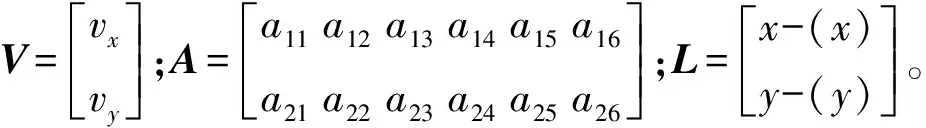
5 实验结果分析

为了验证算法精度，在完成相机标定后将飞机拉至跑道中轴线，将飞机移动25个位置，分别用全站仪对25个位置下飞机标志点进行测量，由于全站仪测量精度可达到3 mm故其测量值可视为真值，与文中算法测量结果进行比对，即可得出算法误差，其结果如图4～图6和表1所示。

图4 X坐标误差分布

图5 Y坐标误差分布

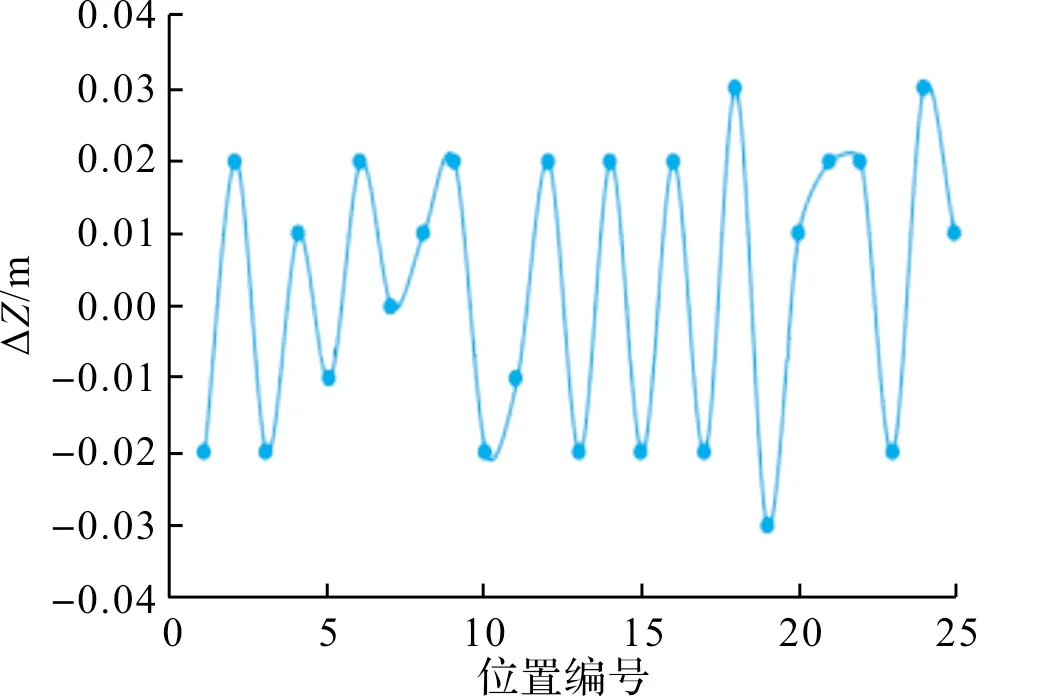
图6 Z坐标误差分布

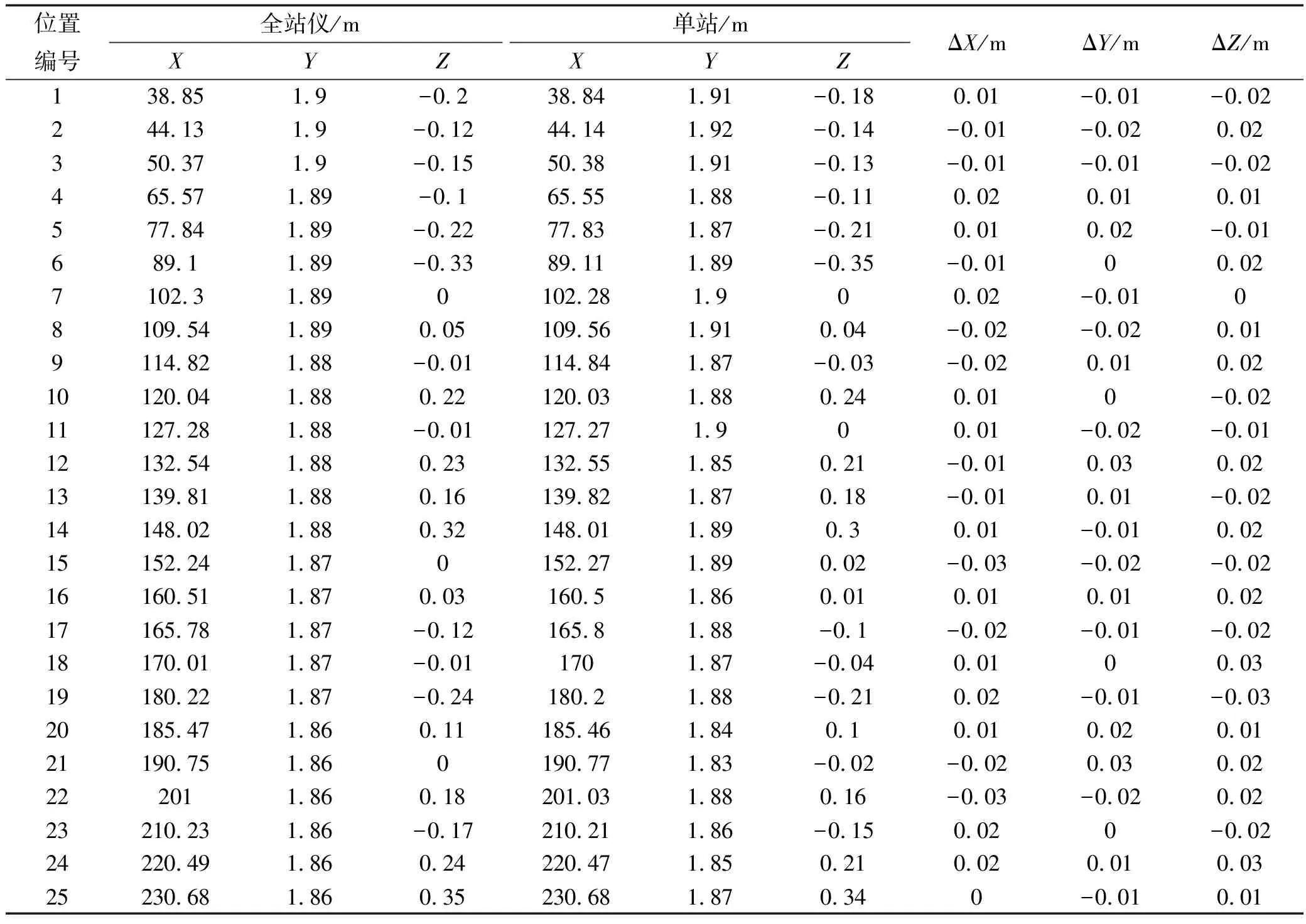
表1 测量结果比对表

从以上对比试验可以看出轴平均误差为1.5 cm，中误差1 cm；轴平均误差1.3 cm，中误差1 cm；轴平均误差1.8 cm，中误差2 cm，测量结果精度满足测量需求，且在后续不同工况下的飞行中测量结果与理论仿真数据均吻合较好，充分证明了算法的有效性，为该型机鉴定提供重要数据支撑。

由于在解算过程中引入飞机惯导数据，惯导数据采样率在25 Hz左右，而高速相机采样率在200 Hz，因此由于采样率差异会对造成影响，但是飞机在起飞过程中加速度往往较大，可看做加速直线运动，其姿态变化较小，尤其与跑道面平面夹角(偏航角)不存在突变情况，因此由采样率差异带来的误差可忽略不计。

6 结论

针对传统近景摄影测量需要多台相机同时交会，导致使用场景大大受限的问题，同时结合试飞任务具体需求，设计了一套单站测量飞机轨迹的系统。利用机上本身抽引的惯导数据，增加单站测量约束条件，在不增加额外成本及设备的情况下，将两台相机交会测量变为单台相机单站测量。一方面节约了试飞测试设备经费，另一方面节约了数据处理周期。经地面及飞行验证，采用的单站测量方法能够将测量误差控制在2 cm以内，满足测量任务精度要求，且系统稳定可靠，降低测试任务成本，提升数据处理效率，具有较高的推广价值。