充填体—围岩组合体力学特性及破裂演化特征RFPA3D模拟
卢宏建 王奕仁 武 婕 武晓军
(华北理工大学矿业工程学院,河北 唐山 063210)
由于地表浅部可用的矿石资源逐渐枯竭,采矿作业正在向地下更深处进行,随之面临地压显现严重、岩爆频繁和采矿成本高等问题[1-2]。充填采矿法在防止地表塌陷和控制采区地压,提高资源回收率和解决矿山废弃物堆存问题等方面的独特优势使其成为深部矿山绿色开采的主要发展方向[3-4],如何确保充填开采过程中采区稳定亦成为行业研究的重点。在回填过程中胶结充填体通常与上下盘围岩共同形成组合结构(图1),对充填体和围岩体的研究虽然已经十分成熟[5-6],但是这种组合结构间相互作用的力学特性和破坏演化特征是判断充填矿房稳定性的基础,仍需要深入研究。
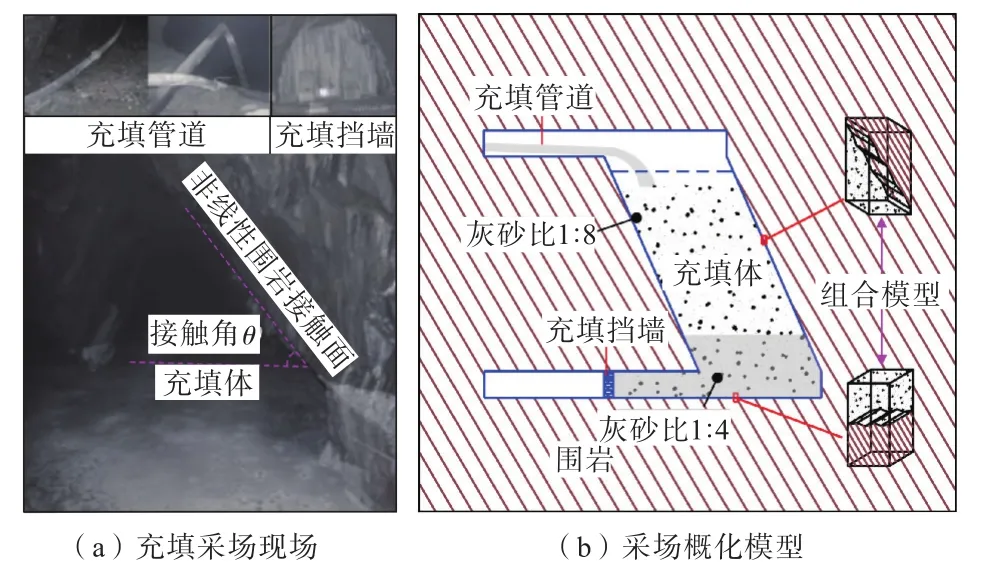
图1 充填体—围岩组合体工程现场与模型Fig.1 Engineering site and model of backfill-rock composite
为了研究胶结充填体—围岩组合结构的力学行为,宋卫东[7-8]通过制作不同岩石—充填体包裹模型,开展侧限压缩和三轴压缩试验,对组合体相互作用机理进行了深入研究;王志国[9]根据矿山实际设计充填体与围岩耦合模型,进行双轴加卸载力学试验,研究了模型破坏过程中的声发射特性;王明旭[10]采用相似材料制作充填体与围岩组合体试件,进行不同条件室内试验,研究了组合体变形演化规律;Wu Weilü[11]通过对不同界面角和水泥含量充填体—围岩组合体的三轴压缩试验,研究了胶结面倾角对组合体三轴变形和抗剪强度的影响。而关于两介质组合模型的研究在煤矿领域较为成熟,曹吉胜[12]运用RFPA模拟软件对不同界面分形维数和倾角特征的煤岩体进行单轴压缩,研究了分界面粗糙度和接触倾角对煤岩体力学特征及破坏机制的影响;左建平[13],宋洪强[14]通过煤岩组合体常规单轴和三轴加载试验,研究原生裂纹和煤岩界面对其力学性质的影响,建立了峰前和峰后的应力—应变关系模型;郭东明[15]通过对不同倾角组合煤岩体进行试验和数值模拟,研究了煤岩组合体中不同倾角交界面对煤岩组合体强度和变形破坏的影响。
国外研究者们针对不同介质组合体的相关研究同样取得了丰硕成果[16-17],在解决矿山实际问题的同时更为开展充填体—围岩组合模型研究提供重要思路和研究手段。然而,充填体—围岩组合体包括充填体、围岩和接触面三部分,特别是接触面受矿体赋存条件和开挖方法的限制,具有非线性和倾角特性。在非线性接触界面下,不同接触角对充填体—围岩组合结构在承压过程中的应力分布以及变形破坏的研究有待完善。本项目借鉴文献[12]建立非线性接触面,以模型组合方式为变量,研究接触角对组合体整体力学性能的影响,同时重点分析组合模型的力学特性和破坏演化特征。
室内试验研究结果虽然更为精确,但是试块制作和试验过程比较复杂,其结果往往存在误差,而数值模拟能很好地解决这一问题,只要模型各细观参数选取合理,模拟结果同样准确可靠。RFPA真实破裂过程分析是一种基于有限元应力分析和统计损伤理论的材料破裂过程分析数值计算软件,其研究结果与真实情况非常接近,逐渐被越来越多的学者应用。Li Gen[18]利用RFPA3D软件,研究了实验室尺度的矩形棱柱岩石试块在无侧限单轴压缩下的破坏机制和断裂形态;Yang Shengqi[19]利用CT扫描技术和RFPA3D模拟软件,研究了不同孔径的空洞岩石试块在三轴压缩下的变形破坏行为。
由于RFPA有限元分析程序在微观/中观到宏观尺度领域研究较为成熟,结果也较为合理可靠,且当前较少学者借助RFPA3D开展充填体—围岩组合体的研究,因此,本研究基于RFPA3D软件,通过对不同灰砂比的充填体、围岩体和接触面非线性的不同界面倾角充填体—围岩组合模型进行单轴压缩试验,分析组合体的破裂演化规律及其应力应变特征。
1 组合体模型单轴压缩数值模拟试验
1.1 试验对象
某金属矿山使用分段空场嗣后充填法开采,矿房和矿柱沿走向交替布置,分两步回采,一步骤矿房回采完毕后进行胶结尾砂充填,待充填体具有自稳定性后回采相邻矿柱。矿体平均倾角为70°,属于急倾斜矿体。为减小料浆对充填挡墙的作用应力,维持采场稳定性,采场底部一般使用高灰砂比尾砂料浆充填,为减少充填成本,采场上部充填低灰砂比料浆。根据矿山充填实际,概化采场模型底部料浆灰砂比1∶4,上部灰砂比1∶8(图1(b)),料浆质量浓度统一为70%。充填体—围岩组合体模型建立与单轴压缩物理试验结果参考文献[20]。
1.2 试验方法
1.2.1 细观力学参数标定
由于充填体属于非均质弹塑性材料,RFPA3D中组合体各部分的非均质度系数(m)采用“试算法”进行确定。数值模拟得出宏观结果(如应力—应变曲线、峰值强度、破坏模式等)用于验证细观参数的可靠性。重复验证过程,通过对比修改不同细观参数对试验结果的影响,定量校准充填体和围岩细观参数,直到数值模拟与物理试验结果相符。参数标定过程见图2。
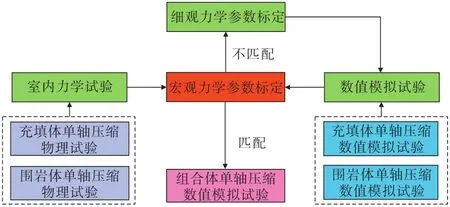
图2 组合体细观参数标定过程Fig.2 Calibration process of meso-parameter of composite
将物理试验中胶结充填体和围岩宏观力学参数转化为细观力学参数,结果如表1所示。不同灰砂比的充填体与围岩数值模拟与物理试验结果见图3。

图3 单轴压缩下不同试块数值模拟和物理试验结果对比Fig.3 Comparison of simulation and physical test results of different test blocks under uniaxial compression

表1 RFPA3D数值模型细观力学参数Table 1 Micro-mechanical parameters of RFPA3D numerical model
1.2.2 组合体模型建立
首先,利用ANSYS软件生成接触面倾角为0°、15°、30°、45°、60°、75°和 90°,正方形底面边长为 50 mm、高度为100 mm的组合体外部数值模型,模型分为上下(0°~60°)或左右(75°~90°)两部分,分别模拟胶结充填体和底板矿柱或围岩(因矿体和围岩强度相近,全部采用围岩)。然后,将建好的组合模型导入RFPA3D软件,设置不同介质材料细观力学参数,主要包括弹性模量、抗压强度、泊松比、摩擦角、非均质度系数等。数值模拟建立的充填体—围岩组合体模型如图4所示。模型单元划分为x×y×z=40×40 ×80,单元总数为12.8万个。
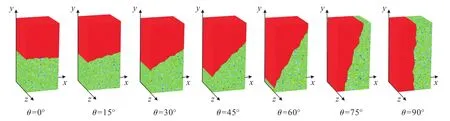
图4 RFPA3D中充填体—围岩组合体数值模型Fig.4 Numerical models of backfill-rock composite in RFPA3D

2 数值计算结果与分析
对构建的7种接触角充填体—围岩组合体开展单轴压缩模拟试验,得到各组模型力学参数见表2,应力—应变曲线见图5。
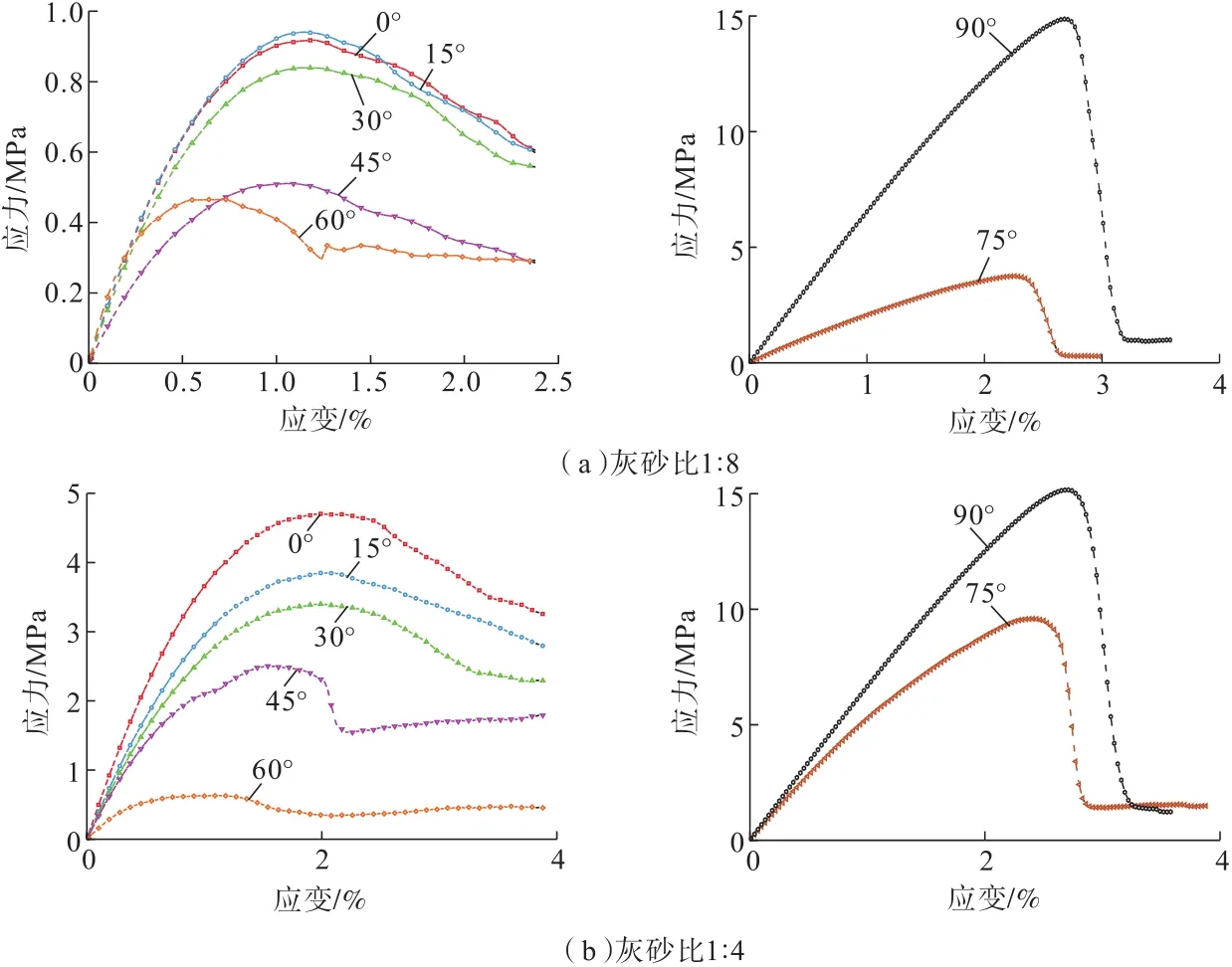
图5 充填体—围岩组合体数值模拟应力—应变曲线Fig.5 Stress-strain curves of numerical simulation of back fill-rock composite
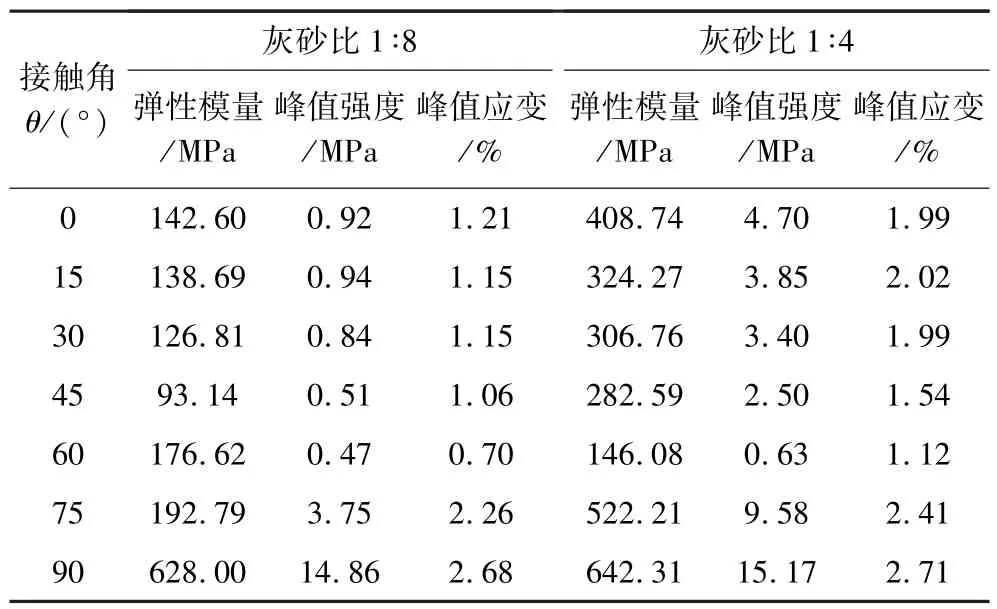
表2 充填体—围岩组合模型单轴压缩数值模拟计算结果Table 2 Numerical simulation results of uniaxial compression of backfill-rock composite models
2.1 组合体力学特征分析
2.1.1 强度特征分析
为深入分析充填体—围岩组合模型强度特征,结合单轴压缩数值试验结果,得到非线性接触面组合体模型峰值应力σc、峰值应变εc与接触角θ关系曲线,如图6所示。分析图6(a),灰砂比为1∶8时,接触角0°~30°的组合体峰值强度接近充填体强度,接触角为45°和60°的组合体峰值强度小于完整充填体和围岩体强度,接触角为75°和90°的组合体峰值强度介于完整充填体和围岩体强度之间;分析图6(b),灰砂比为 1 ∶4 时,接触角为 0°、15°、30°、75°和 90°的组合体峰值强度介于完整充填体和围岩体之间,接触角为45°和60°的组合体峰值强度小于完整充填体和围岩体强度,可知充填灰砂比的大小会影响不同接触角下充填体—围岩组合体强度分布,在接触角为45°和60°时,组合体强度受接触角的影响明显。

图6 组合模型峰值强度与接触角关系Fig.6 Relationship between peak strength and interface angle of composite models
2.1.2 变形特征分析
根据试验结果可得到组合模型峰值应变与接触角关系如图7所示。
综合分析图7(a)和图7(b),当灰砂比为1∶8时,接触角为0°~75°的组合体峰值应变小于完整充填体和围岩体应变,接触角为90°的组合体峰值应变介于完整充填体和围岩体之间;当灰砂比为1∶4时,接触角为0°~90°的组合体峰值应变均小于完整充填体和围岩体应变,可知充填灰砂比大小会影响充填体—围岩组合体变形能力,灰砂比越大组合体变形能力越强。对比完整充填体和围岩体峰值应变,可知接触面会减弱两介质组合体变形能力,接触角为60°的组合体变形能力最弱,接触角为90°的组合体变形能力最强。
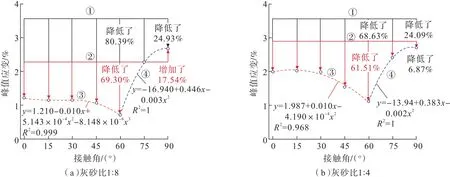
图7 组合模型峰值应变与接触角关系Fig.7 Relationship between peak strain and interface angle of composite models
2.1.3 弹性模量特征分析
根据表2中数据,可得到组合体弹性模量E与接触角θ之间的关系,如图8所示。
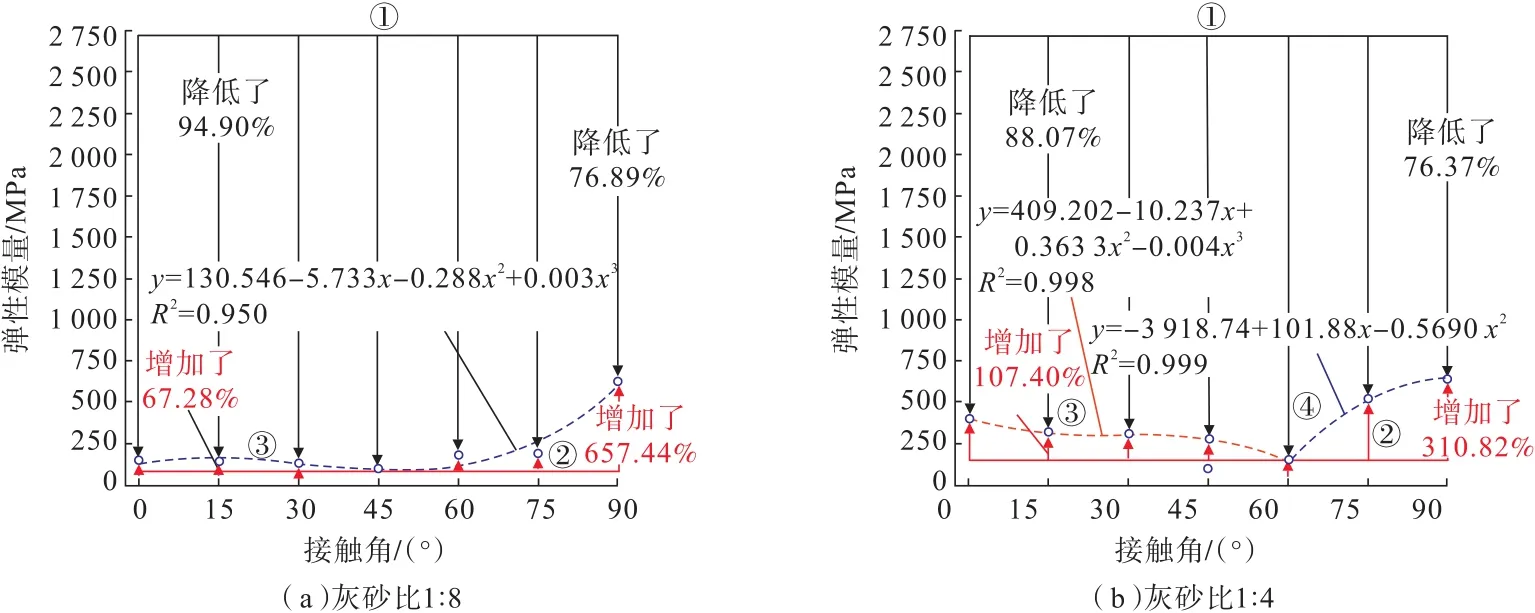
图8 组合模型弹性模量与接触角关系Fig.8 Relationship between elastic modulus and interface angle of composite models
综合分析图8可知,组合体弹性模量介于完整充填体和围岩体之间,灰砂比为1∶8时,接触角为45°的组合体弹性模量最小。灰砂比为1∶4时,接触角为60°的组合体弹性模量最小。接触角为90°的组合体弹性模量均最大。且充填灰砂比越大,组合体弹性模量越大。
2.2 组合体破坏演化特征分析
从各组合体损伤演化过程看出,最初损坏的材料细观单元在模型中是无序分布的,它们可能是具有随机位置和大小的单个点或局部带。随着荷载进一步增加,受损材料细观单元趋向于集中在模型中心接触带部分,形成细观裂缝。细观裂纹进一步扩展、集中和跨尺度增长导致宏观断裂形成。此后,观察到典型宏观裂纹扩展过程,伴随着新的细观裂纹萌生和发展。篇幅所限,本文仅以接触角60°组合体为例进行分析,根据应力—应变的特征形式,为便于描述组合体变形破坏演化过程,在试验曲线上设置了标识点a~f,如图9(a)、图9(b)所示。其中,损伤云图中红色区域表示弹性区,蓝色和绿色点表示损坏单元;声发射信号点图中,深蓝色球体表示剪切破坏单元,红色球体表示拉伸破坏单元,球体大小表示信号强弱。
由图9(a)可知,灰砂比 1∶8,θ=60°的组合体在受载初期(标识点a),上部充填体随机分布少量的剪切和张拉破坏单元。当进入塑性阶段直至应力峰值(标识点b~c),由于材料强度的差异,损伤单元率先出现在充填体上,随着荷载增大,破坏单元由充填体向接触面处发展,标识点c处为应力峰值,此时上接触面处的损伤单元更为明显,充填体单元破坏由剪切应力主导,仅有极少数单元发生张拉破坏。在应力峰值后(标识点d~f),组合体内部充填体单元破坏程度变缓,但是接触面处的损伤单元增长较多,标识点d~e段内,应力曲线出现回弹,此时接触面单元破坏由受剪切应力控制转变为受张拉应力控制。分析这一现象,接触面附近,由于2种材料变形趋势的差异,在组合体发生破坏前,充填体受到横向约束压缩应力,围岩受到横向约束拉伸应力。随着充填体破坏的发展,2介质间的约束作用逐渐消失,上接触面充填体出现张拉破坏,说明在非线性接触面下这种破坏控制应力的转变过程会导致应力曲线的回弹,提升了组合体的整体抗压强度。
由图9(b)可知,灰砂比 1∶4,θ=60°的组合体在受载初期(标识点a),沿倾斜接触面上端出现剪切破坏,接触面中部出现少量张拉破坏单元。当进入塑性阶段直至应力峰值(标识点b~d),随着荷载的增加,组合体上部充填体损伤单元持续增多,标识点d处为应力峰值,此时沿接触面上部的充填体损伤单元更加密集,组合体沿接触面发生剪切破坏并伴随张拉破坏。分析这一现象,说明在塑性发展阶段随着充填体破坏,下部围岩对上部充填体的约束作用逐渐消失。应力峰值后(标识点e~f),组合体单元破坏由剪切应力控制转变为由张拉应力控制,组合体发生沿着接触面的剪切—张拉组合破坏,应力曲线出现回弹。标识点f处,充填体表面出现多条剪切裂纹与加载方向成30°~45°夹角。
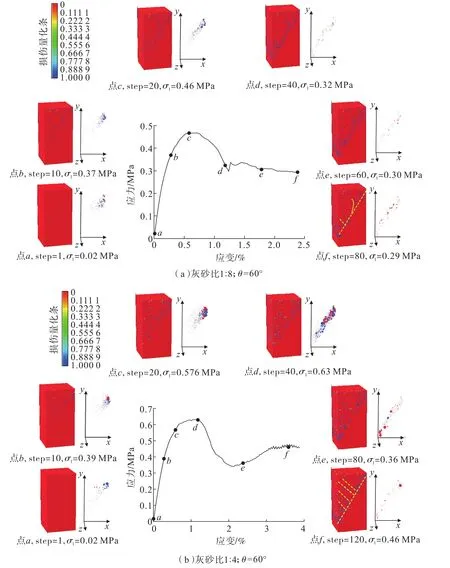
图9 单轴压缩下组合体声发射和损伤演化图Fig.9 Acoustic emission and damage evolution diagrams of the composite under uniaxial compression
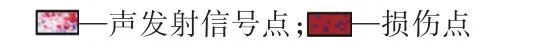
通过对不同倾角充填体—围岩组合模型单轴压缩损伤及声发射信号点演化过程分析,不难发现,受不同材料变形特征差异的影响,接触面附近上下介质受到不同方向的约束应力作用,且随着破坏的进行这一相互约束作用应力逐渐消失,非线性接触面处控制单元损伤的应力发生转变,这一转变过程在不同倾角下在应力曲线表现出不同特征,在θ=45°~60°时,这一现象最为明显且会导致应力曲线发生回弹。除了各组合体表面沿接触面出现宏观剪切裂纹外,衍生的剪切或张拉裂纹与加载方向成30°~60°夹角,形成宏观剪切—拉伸混合裂纹。接触角0°~30°组合体中仅充填体发生损伤;接触角45°~90°组合体损伤起始点都出现在充填体上,随着加载进行损伤逐渐在接触面附近汇聚,其中,45°和60°组合体破裂受接触角和充填体强度影响较大,75°和90°组合体破裂受围岩强度和接触角影响较大。张拉应力是造成横向裂纹和破碎区的主要原因,剪切应力是造成二次裂纹(次生裂纹)出现的主要原因。
不同灰砂比,不同接触角组合体的最终破坏形式如图10所示。θ=0°~30°组合体充填体表面多出现斜剪切裂纹和与之垂直的张拉裂纹,θ=45°~90°的组合体不规则的二次裂纹与接触面裂纹交错形成树枝状裂纹系统伴生挤压破碎区,可分为 Y形(45°和60°)和反 N 形(75°和 90°)。 随着组合体接触角增加,试块破坏形式逐渐由张拉破坏主导(θ=0°~30°)转变为剪切破坏主导(θ=45°~60°),最终转变为剪切—张拉组合破坏(θ=75°~90°)。
图10 单轴压缩下组合体破坏模式对比Fig.10 Comparison of failure models of composite under uniaxial compression
3 结 论
(1)随着接触角(θ)增大,组合体模型的峰值应力σc、峰值应变εc、弹性模量E先减小后增大。随灰砂比增大,各参数均增大。 θ=60°时,σc和 εc最小;θ=15°时,E最小;θ=90°,各参数均最大。受θ和灰砂比的影响,组合体σc和εc并非完全介于充填体和围岩体相应参数之间,但是E始终处于2介质弹模之间。
(2)组合体破坏为宏观剪切—张拉混合裂纹。沿接触面出现宏观剪切裂纹,充填体内衍生的剪切裂纹与模型加载方向所成角度约为30°~60°。 张拉应力是造成横向裂纹和破碎区的主要原因,剪切应力是造成二次裂纹(次生裂纹)出现的主要原因。不规则二次裂纹与接触面裂纹交错形成树枝状裂纹系统,分为 Y 形(45°和 60°)和反 N 形(75°和 90°)。
(3)接触角 0°~30°组合体破坏发生在充填体区域为张拉破坏,接触角45°~60°组合体破坏发生在充填体和接触面区域为剪切破坏,接触角75°~90°组合体破坏发生在充填体、接触面和围岩区域为剪切—张拉组合破坏。

