基于频域低秩矩阵补全的气象雷达WTC抑制算法
邱存银, 沈明威, 韩国栋
(1. 河海大学, 江苏 南京 211106;2. 中国电子科技集团公司第五十四研究所, 河北 石家庄 050081)
0 引 言
随着能源不断的被开发利用,煤炭、石油等不可再生能源正在不断枯竭,世界各国对可再生能源的需求也更加强烈。近年来,诸多国家对风电等的研究逐步深入,技术也愈发成熟,这使得风电场的数量和规模呈指数倍增加。然而研究表明,风力涡轮机大型叶片高速旋转会造成雷达回波的多普勒频谱持续展宽,气象目标被淹没于风力涡轮机杂波(Wind Turbine Clutter,WTC)的多普勒频谱中,严重影响了雷达系统对气象目标检测的精确性[1-3]。因此,国内外学者详细分析了气象雷达不同工作模式下风力涡轮机杂波WTC与气象回波的时、频域分布特性,发现由于WTC的时变性,使得针对静止杂波的时域滤波、频域滤波等传统杂波抑制技术均失效,此时传统的杂波抑制技术无法在抑制WTC的同时无损恢复气象信息[4-9]。
针对上述问题,本文根据气象信号的低秩分布特性,将稀疏优化理论引入到WTC抑制中,研究了基于矩阵补全(Matrix Completion,MC)的气象雷达WTC杂波抑制新方法。MC算法是一种源于压缩感知的秩最小化理论,其主要作用是在存在数据缺失或只能观测到部分数据的低秩观测矩阵中,利用矩阵元素之间的相关性,有效地恢复矩阵的缺失数据[10]。本文的目的是在气象信号矩阵受到WTC污染后,利用MC对污染后缺失的数据进行填充恢复,在抑制WTC的同时还能够精确恢复气象信号矩阵。另外将常用的频域多重二次插值与频域MC算法进行对比,理论分析和实验结果表明,频域MC算法较频域多重二次插值能更好地恢复受WTC干扰的气象信号。
1 雷达回波数据预处理
在雷达系统中,假设距离单元同时包含WTC和天气信号。在本文实验中给定被污染的方位-距离单元在相干积累时间(Coherent Integration Time, CIT)内接收到的信号表示为
xl(m)=sl(m)+cl(m)+wl(m)+nl(m)
(1)
式中:m=1,2,…,M,M是脉冲个数;l为某一距离单元;sl(m)为气象信号;cl(m)为地杂波信号;wl(m)为WTC;nl(m)为其他噪声信号。
由于杂波集中在零频附近,对气象信号不造成干扰,因此设计脉冲可以将其滤除。此时,被污染的雷达方位-距离单元在CIT内接收到的信号可表示为
xl(m)=sl(m)+wl(m)+nl(m)
(2)
信噪比(Signal to Noise Ratio,SNR)是影响气象信号恢复精度的决定因素。因此,可将实测数据的雷达回波信号从时域转换至多普勒频域,通过相干积累提高SNR,这一过程可通过快速傅里叶变换(Fast Fourier Transform,FFT)实现。多普勒频域的气象信号X(k)为
k=1,2,…,K,l=1,2,…,L
(3)
式中:K为地杂波对消后的脉冲数;L为距离单元。在频域进行矩阵元素补全,以实现低SNR情况下,被污染距离单元气象信号的高精度恢复。
2 频域矩阵补全算法
2.1 低秩矩阵重构
文献[11-12]证明了当矩阵的奇异值具有稀疏性(即矩阵是低秩的)且采样数目满足一定条件时,大多数矩阵可通过求解核范数最小化问题来精确地恢复所有元素。所以对于任何抽样的数据,如果将一行或一列作为一个整体进行抽样,那么此时观测矩阵不能满足元素采样集均匀随机采样的条件,缺失的元素也就不能被高精度恢复。因此,需选取特殊的矩阵形式重新构造观测矩阵,使信号的采样点随机分布在整个回波数据中,满足低秩重构的条件。
对于预处理后的多普勒域信号X(k),将其重构成k1×k2维的Hankel矩阵,其中k1+k2-1=L。用杂波检测算法提取出WTC所在距离单元l,并将干扰元素置零,在重构的矩阵中,这些零元素将被重新排列以进行随机采样[13]。根据Hankel矩阵模型和式(1),取气象信号距离-多普勒频域矩阵的第k列,构造的Hankel矩阵S如下

构造一个方阵B=S×SH,根据矩阵的特征分解理论,可以得到
(4)
式中:Σ=diag(σ1,σ2,…,σr),σi为矩阵S的全部奇异值;V为特征向量排成列的矩阵。根据r(SSH)=r(S),因此,矩阵B秩的数值可由该矩阵的奇异值数量推导得出。假设k=470,则矩阵B的特征值分布如图1所示。
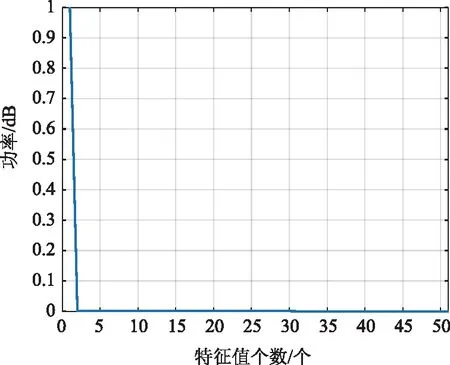
图1 仿真数据构建的Hankel矩阵特征值分布
图1为气象信号仿真数据下构建的Hankel矩阵特征值分布,可以明显看出,重构Hankel矩阵的秩r=2≪51,此时观测矩阵满足所需低秩的要求[14]。
2.2 基于NNM-IALM算法的WTC抑制
矩阵补全是一种重建随机抽样低秩矩阵或近似低秩约束的过程。根据MC理论,当雷达回波信号被WTC污染时,可去除所有被污染的样本,只保留剩余的气象数据,即可将对WTC抑制转化为一个矩阵补全问题。
根据上述Hankel矩阵的构造方法,将预处理后的频域信号第k个脉冲下的列向量构造为Hankel矩阵X。同理,用S,C,W,N分别表示构造的关于Sl(k),Cl(k),Wl(k),Nl(k)的Hankel矩阵。
为了解决上述矩阵补全问题,构造一个矩阵补全模型,通过约束秩最小化的问题,根据已知的矩阵元素补全未知元素。去除WTC后,气象数据可以通过下式中核范数最小化(Nuclear Norm Minimization,NNM)模型进行恢复
(5)
其中,
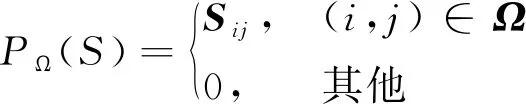
(6)
式中:min(·)表示最小化;‖·‖*为矩阵的核范数;PΩ为正交投影算子,表示投影到仅在指标集Ω非零的稀疏矩阵子空间上的映射。
利用文献[15]中非精确增广拉格朗日乘子(Inexact Augmented Lagrange Multiplier,IALM)求解式(4)中的优化问题时,将其扩展到复数域,其对应的拉格朗日函数可表示为
L(S,N,Y,μ)=‖S‖*+〈Y,X-S-N〉+
‖S‖*+tr(YH((X-N)-S))+
(7)
定义一个收缩运算符为
(8)
利用IALM交替更新S,N,Y,μ,其迭代步骤如下。
步骤1:固定变量N,Y和μ,更新变量S
(9)
对X-Nk+μk-1Y进行奇异值分解
(U,Σ,VH)=svd(X-Nk+μk-1Yk)
(10)
则S的迭代更新公式为
Sk+1=UT(2μk)-1[Σ]VH=
(11)
步骤2:固定变量S,Y和μ,更新变量N
(12)
对式(12)中的N进行求导可得:
(13)
步骤3:固定变量S,N和μ,更新变量Y
Yk+1=Yk+μ(X-Sk+1-Nk+1)
(14)
步骤4:更新变量μ
μk+1=ρμk
(15)
其中,Y表示拉格朗日乘子矩阵;μ>0表示惩罚因子;ρ为观测数据率;
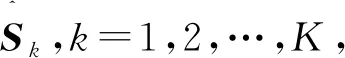
3 实验结果与分析
本节通过计算机验证算法的性能,本次实验使用的实测数据来自于荷兰代尔夫特理工大学的IDRA雷达[16]。实测数据参数如表1所示。
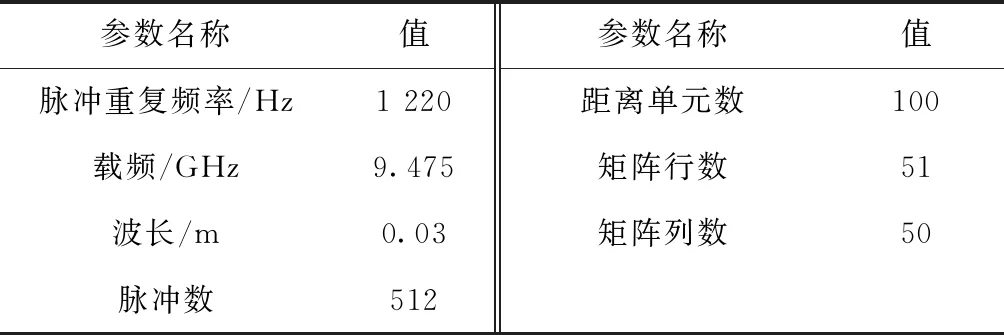
表1 Hankel矩阵仿真参数
选取气象信号实测数据的第30个距离单元作为本次实验被污染的距离单元,由图2(a)可知,气象信号分布在425 Hz~526 Hz,在第30个距离单元中加入WTC,从图2(b)可以看出,气象信号淹没在WTC中。图2为被WTC污染前后的多普勒图。
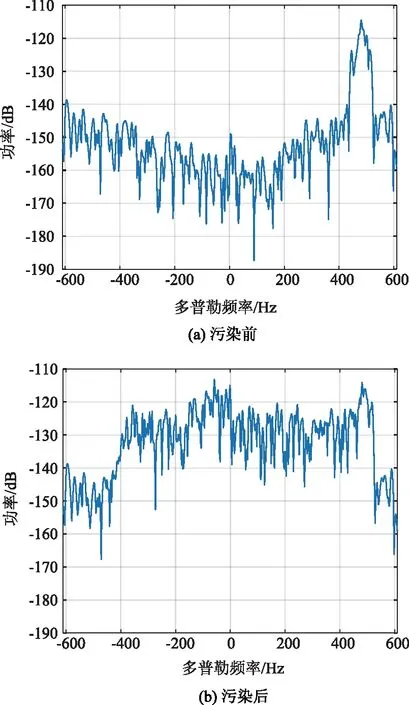
图2 加入WTC前后气象信号多普勒图
从图3可以看出,实测数据构建的Hankel矩阵特征值分布下降的趋势相较于图1仿真数据构建的Hankel矩阵更缓慢,该现象主要是由实测数据中噪声成分的复杂性造成,但近似满足低秩特性,因此可采用MC方法高精度恢复气象信号[17]。
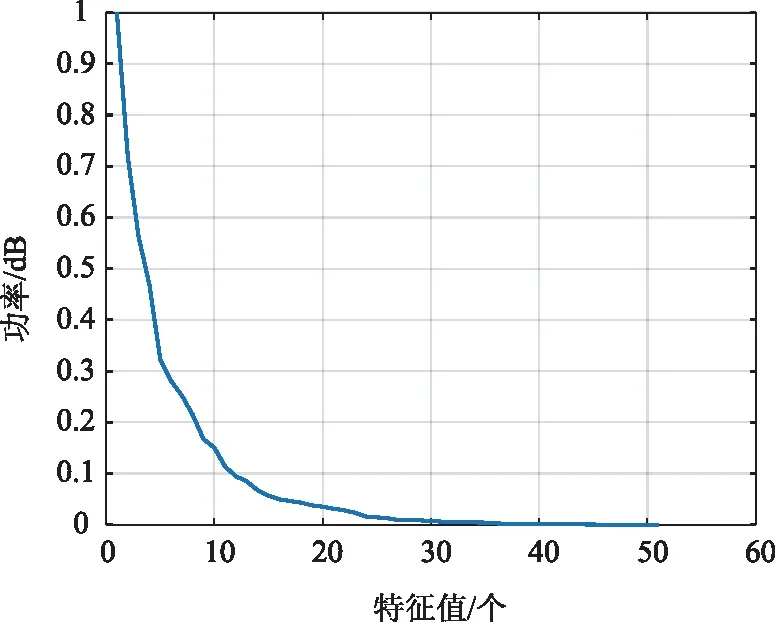
图3 实测数据构建的Hankel矩阵特征值分布
图4为分别使用频域多重二次插值、时域NNM-IALM和频域NNM-IALM算法恢复的气象信号多普勒图。从图中可以看出,三种算法都可以有效抑制WTC并恢复气象信号。但是在气象信号恢复的精度上,频域NNM-IALM算法恢复的效果明显优于频域多重二次插值算法和时域NNM-IALM算法,这是由于在矩阵补全实验前对实测数据的雷达回波信号进行预处理,将雷达回波信号从时域转换至多普勒频域,通过相干积累提高SNR,进而提高实验的恢复精度。另外在时域的条件下对气象信号补全,不仅不能抑制噪声而且气象信号的旁瓣较高,对气象信号的恢复产生了影响,这一问题在多普勒频域实现补全时得到了解决。在实际工程应用中,并不需要将所有频点处的信号恢复,我们只需恢复气象信号所在的频率范围即可,这样可极大的减少运算量。

图4 不同算法恢复出的气象信号功率谱
使用FFT法对气象信号的径向速度与谱宽进行估计,将两种算法的谱矩结果与真实数据做对比,采用交叉验证法来评价两种算法的性能。
根据谱矩估计量的定义,信号功率表示为
(16)
平均频率表示为
(17)
谱宽表示为
(18)
式中:S(fi)为信号功率谱fi=i/KTr,i=1,2,…,K,Tr为脉冲重复间隔;K为脉冲个数。
气象回波的径向速度和速度谱宽分别为
(19)
(20)
由实验估计出被WTC污染的第30个距离单元气象信号的径向速度和谱宽如表2所示。
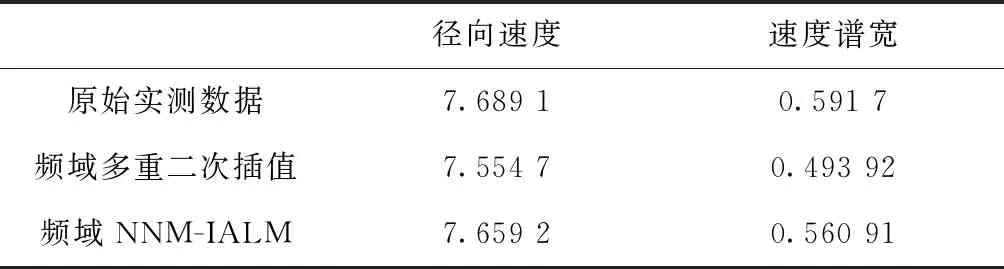
表2 仿真数据性能对比 m/s
由表2的实验数据可以看出,在相同的实验环境下,频域NNM-IALM算法比频域多重二次插值能更精确的恢复出气象信号,恢复后的径向速度和速度谱宽也更接近原始的实测数据且估计精度比频域多重二次插值算法分别提高了约22.25%和31.48%。综上,频域NNM-IALM算法能够更好的抑制WTC,并有效恢复被污染的气象信号。
4 结 语
本文将频域矩阵补全运用到气象雷达实测数据的WTC抑制中。把预处理后的多普勒域回波信号重构为等效的低秩矩阵,并通过IALM算法来有效地恢复缺失数据,同时在相同的实验条件下与频域多重二次插值进行对比。实验结果表明,上述两种方法都达到了杂波抑制的效果,实现了气象信号的恢复。但基于Hankel矩阵构建的高精度频域补全算法无论在恢复性能还是降噪效果上都更优,并解决了低信噪比下时域矩阵补全的高旁瓣问题。

