基于最大熵原理的钠液滴粒径分布模型开发
邹文斌,佟立丽,曹学武
基于最大熵原理的钠液滴粒径分布模型开发
邹文斌,佟立丽*,曹学武
(上海交通大学机械与动力工程学院,上海200240)
钠雾火事故是快堆安全分析的重要对象之一,液钠在系统压差下向外界喷射所形成的液滴粒径分布是影响钠雾火事故危险程度的关键因素之一。为预测钠雾火事故中液滴粒径的分布情况,基于最大熵原理,以质量守恒方程作为主要约束条件,推导了钠液滴粒径分布的理论模型;为方便应用,基于雾化燃料、液钠开展的粒径分布实验数据,通过拟合方法获得了半经验关系式,描述了钠液滴粒径分布与压差间的关系。最后,通过与氩气气氛钠喷射试验获得的不同压差下钠液滴平均粒径实验数据的比对,验证了该模型,且预测相对误差可以控制在30%以内。该模型也反映出伴随压差的增加,钠液滴的平均粒径逐渐减小。
钠雾火;钠液滴;粒径分布;最大熵原理
当钠冷快堆回路中的液态钠泄漏并与空气接触时,就会发生燃烧现象。燃烧最终不仅会产生大量气溶胶,过程中迅速释放的热量也将对系统和设备造成严重的热冲击,可能导致设备的损坏[1,2]。因此,针对钠冷快堆的钠火事故评估是快堆安全评审最重要的部分之一,而阐明钠火过程中的重要物理现象与规律,是开发快堆安全分析工具,并建立事故缓解及应急对策的重要支撑,对进一步研发钠冷快堆有着直接而积极的意义。
雾状钠火作为钠火事故中特征典型、后果最为严重的一种现象[3],受到了国内外学者的广泛关注。为了解雾状钠火的燃烧机理及后果,首先需研究钠由回路中喷射释放时所形成分散液滴的尺寸分布,该分布特征可为后续钠雾火现象的进一步发展提供确定的初始条件。早期,SPRAY软件采用对数正态分布的数学表达式描述钠液滴在泄漏后的粒径分布,但通过与Atomics International Jet Test No.4实验数据的比对后发现,该分布不能较好地反映实验结果[4]。随后,布鲁克海文国家实验室的Tsai等人采用Nukiyama-Tanasama关联式开发了NACOM软件用以计算钠雾火现象,并一度获得了改良后的计算结果[4,5]。2017年,中国原子能院自主建立了钠雾火实验装置[3],并开展了不同喷口压差作用下的钠液滴分布实验及钠雾火燃烧实验,并采用NACOM软件进行了试算,试算结果反映出NACOM分析程序不能很好地模拟钠喷射期间的压力变化及钠喷射结束后的温度变化,这可能由于反映钠液滴粒径分布的Nukiyama-Tanasama关联式不能适用于不同压差作用的结果。由此,需要针对钠液滴在发生泄漏时的粒径分布过程建立新的关系式,考虑压差作用的影响,以便对开发钠雾火安全分析程序提供经过实验验证的理论模型。
最大熵原理最早是由Jaynes在1957年提出,常用于求解满足一系列约束条件下,某体系中各物理量的最概然分布问题[6]。因此,很多学者采用此方法对能源领域的燃油燃烧问题开展了初步探索[7,8]。曹建明[9]曾基于最大熵原理获得了以质量、动量和能量方程为主要约束条件的柴油喷雾燃烧模型解的形式,但由于求解矩阵中涉及复杂的高非线性一重积分项,解析解无法获得。之后,其进一步化简了该过程,抓住了初始动量的主要影响,以单一动量方程作为主要约束条件,得到了喷雾液滴尺寸和速度联合分布函数,并编写了KIVA-Ⅱ程序进行数值求解[10]。由于作者并未对模型开展实验验证,其对于不同系统压差作用下的响应情况不得而知。本文主要针对钠雾火现象中的液滴分布问题,基于最大熵原理及其模型推导逻辑,以质量守恒方程作为主要约束条件,建立反映钠液滴分布和系统内外压差间的数学模型,并采用国内外典型钠液滴分布实验数据开展验证,研究成果可为我国自主研发钠火安全分析程序提供模型基础。
1 钠雾火液滴粒径分布模型的建立
1.1 约束条件的确定
信息熵采用公式形式表达如下:
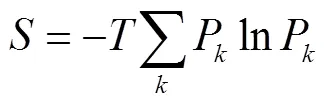
式中:
——常数;
k——某泄漏钠液滴直径下液滴的数目概率。
当此系统内全部约束条件被满足且信息熵取极大值时,最概然事件发生,即取得了发生概率最大的钠液滴粒径分布函数,存在公式(2):
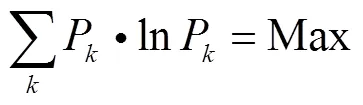
由系统内钠液滴质量守恒,得公式(3):
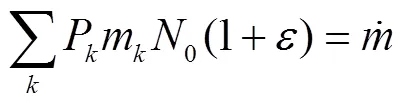
式中:
考虑钠液滴为不可压缩流体,则式(3)可转换为式(4)
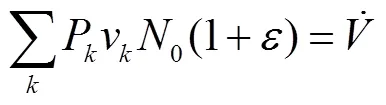
式中:
由于各种情况下,数目概率总和为1,即公式(5):
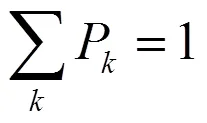
1.2 控制方程的求解
针对以上3个基本约束条件,采用拉格朗
日因子法,得到函数如公式(6):
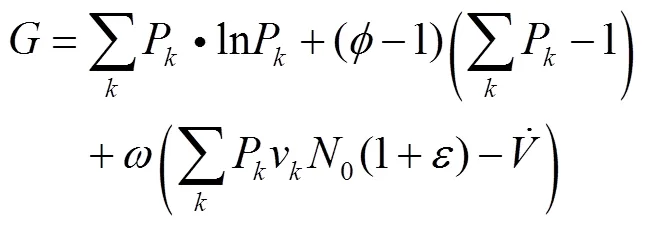
令:
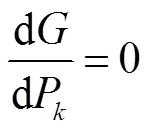
则:
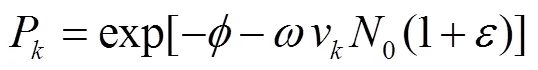
将式(8)代入式(5),
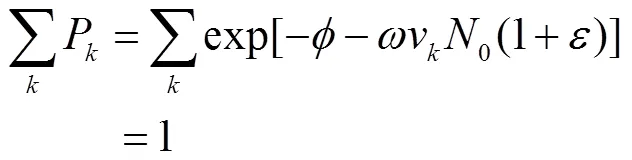
即:
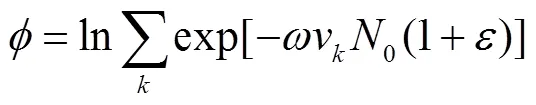
将式(8)代入式(4),
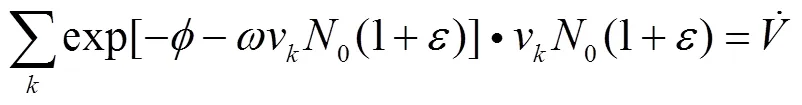
即:
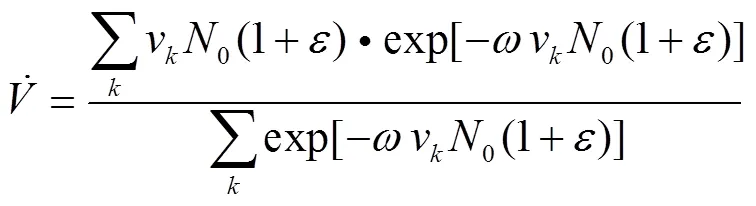
假设由回路系统破口喷出的钠液滴雾化粒子粒径符合连续性分布,则由式(11)可得式(13),
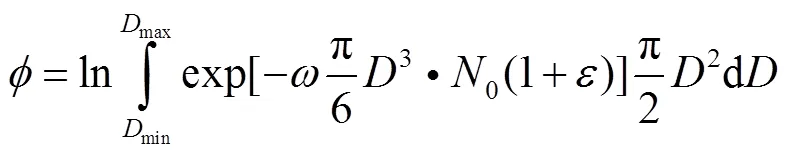
求解得式(14):
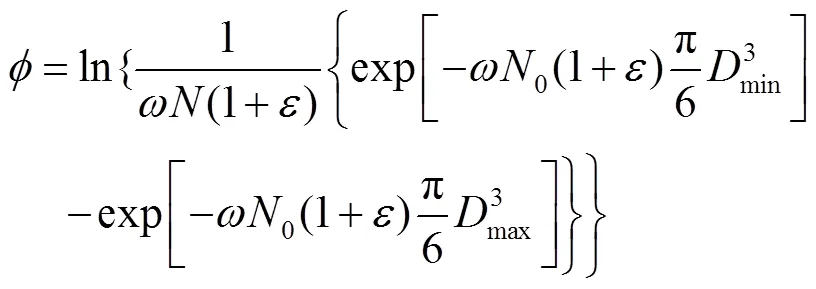
同理,由式(12)可得式(15):
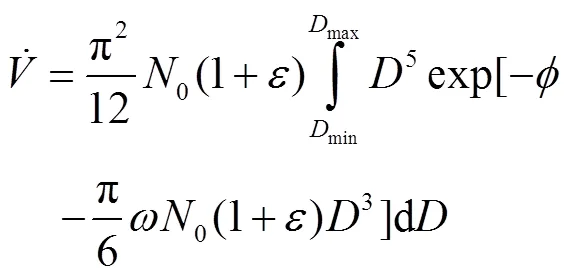
将式(14)代入式(15)并积分可得,
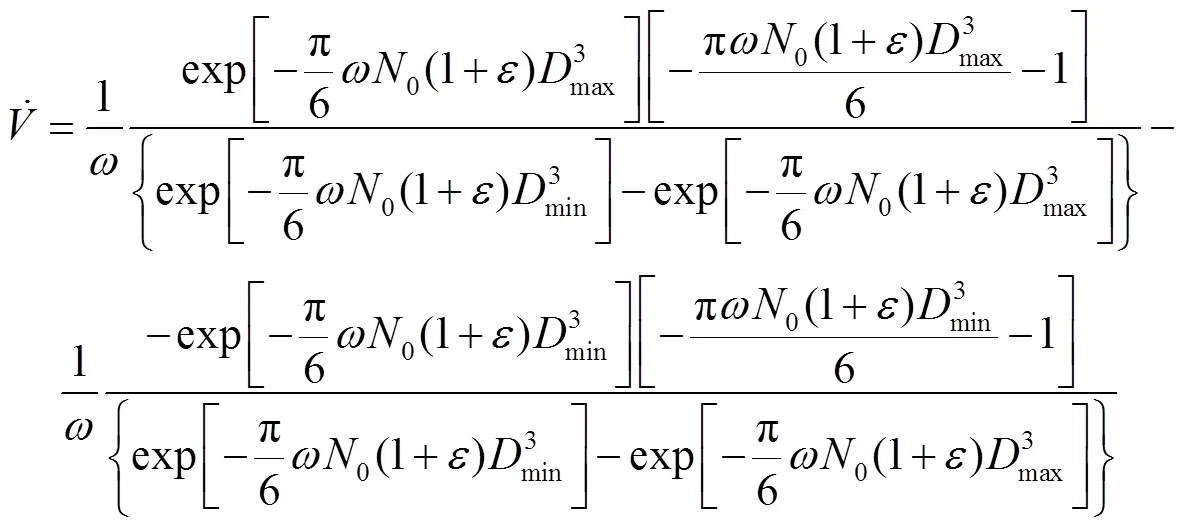
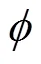
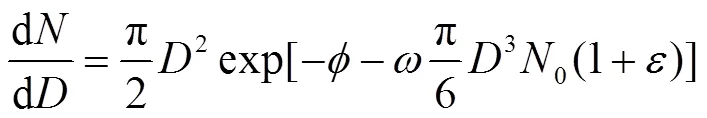
式中:
——尺寸为的钠液滴的数量百分数;
d/d——直径为的钠液滴的概率密度函数。
考虑在破口处钠回路系统与外界环境间存在压差驱动,假设喷出后钠液滴的最小直径为0,最大直径为cr,由临界数确定,可以表示为式(18)。
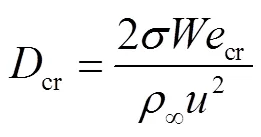
则简化(14)后可得,
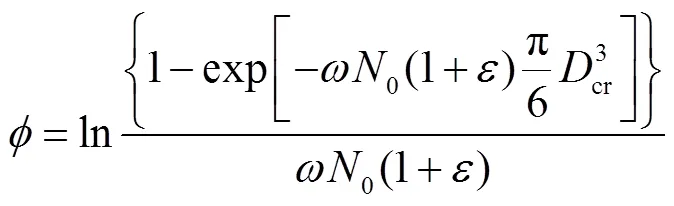
将式(19)代入式(17),
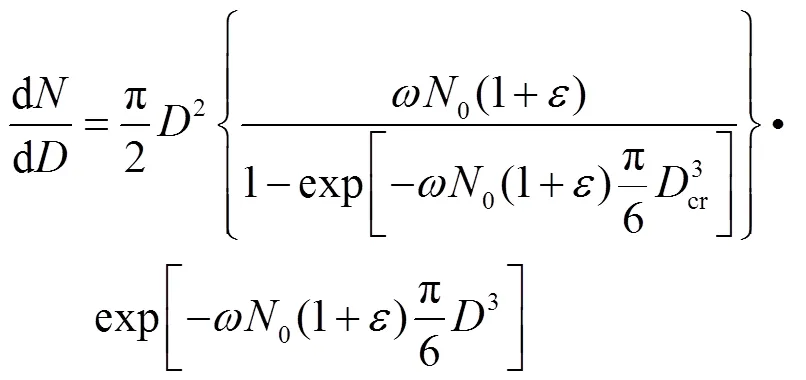
1.3 经验系数的拟合
式(20)可以简化表示为式(21)
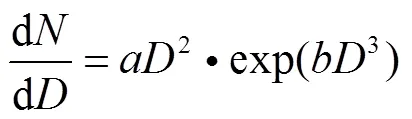
即通过钠雾火粒径分布实验数据确定经验系数与后,即能快速建立粒径分布的理论分析模型。进一步,对式(21)进行对数处理,可以获得实验数据需拟合的数学表达式形式,如式(22)。
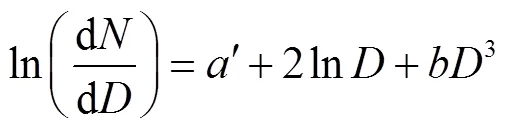
南京理工大学针对HAN基液体模拟工质,曾分别开展了压差为1.8 MPa、2.2 MPa及2.6 MPa下喷雾液滴粒径的分布实验[6],采用公式(22)对其实验数据进行拟合,结果如图 1所示。
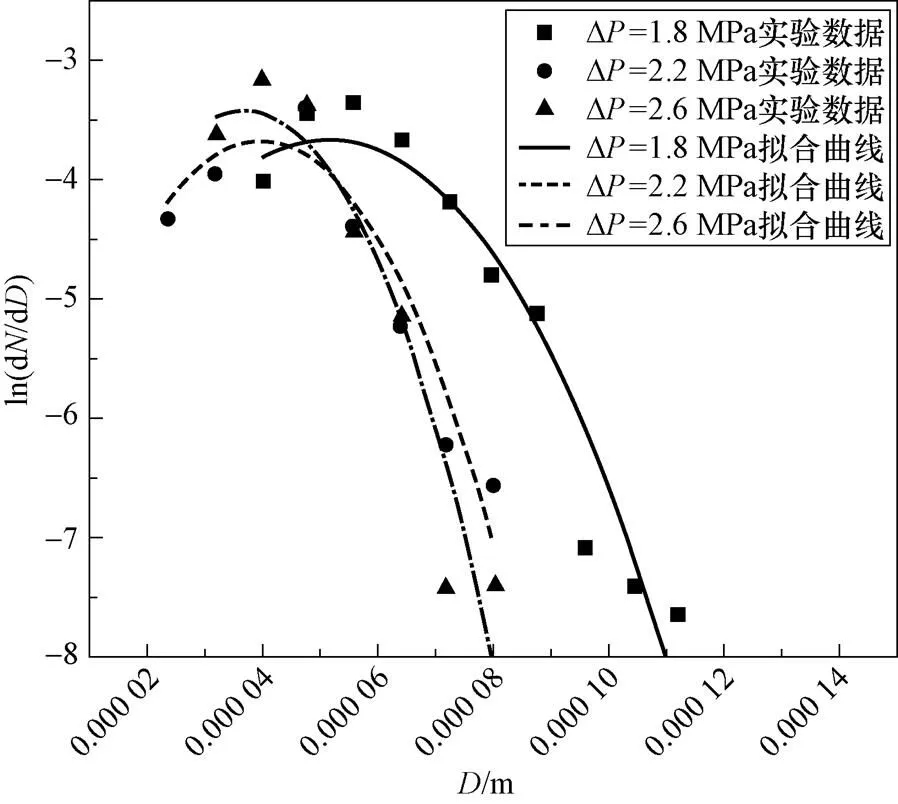
图1 HAN基液滴粒径分布实验数据拟合结果
系统内外压差为1.8 MPa、2.2 MPa及2.6 MPa下,理论模型的经验系数分别如式(23)~式(25)所示。可见,该经验系数与系统压差存在关联。
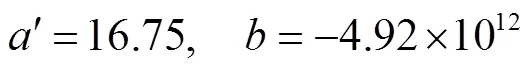
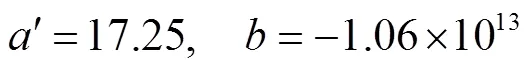
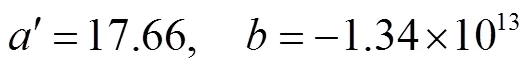
中国原子能院曾开展钠雾火实验,并在第一阶段的研究中,开展了不同压差作用下的钠液滴粒径分布实验[11],下面针对钠液滴温度为250 ℃,压差为0.15 MPa的液滴粒径分布实验数据进行拟合,拟合结果如图2所示,确定的待定系数如式(26)所示。
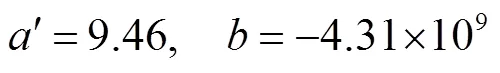
意大利曾开展LISOF实验以研究钠冷快堆小破口下的液滴泄漏现象[12],针对压差为6 bar(g)工况下的可视化钠液滴分布实验数据的拟合结果如图3所示,确定的待定系数如式(27)所示。
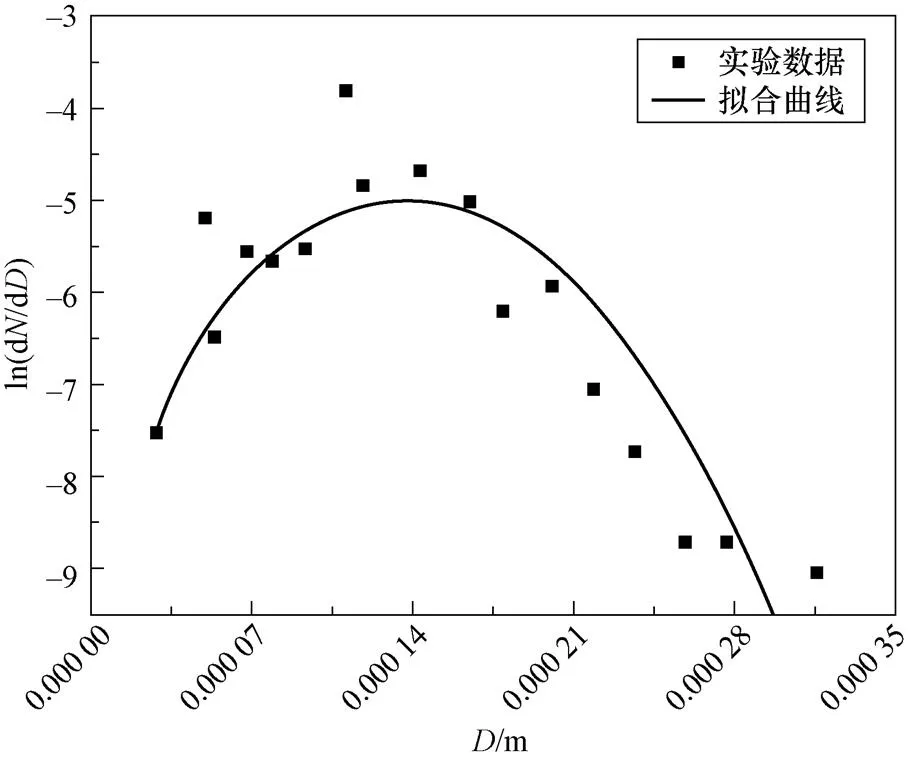
图3 钠液滴粒径分布实验数据拟合结果
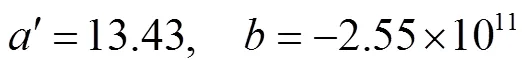
日本Hiroyasu等曾开展喷雾试验将柴油喷入定容室内处于室温与高压下的静态空气中,其喷射压力9.9 MPa,环境压力为1.1 MPa。所获实验数据的拟合结果如图4所示,确定的待定系数如式(28)所示。
1.4 经验系数与压差间的关系
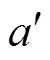
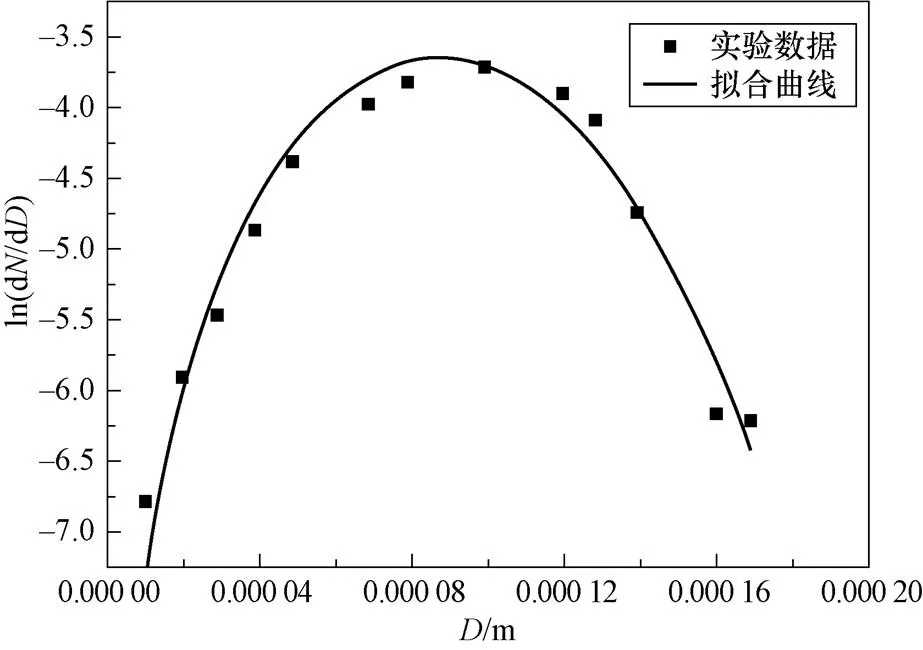
图4 轻质柴油粒径分布实验数据拟合结果
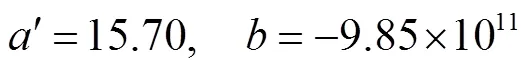
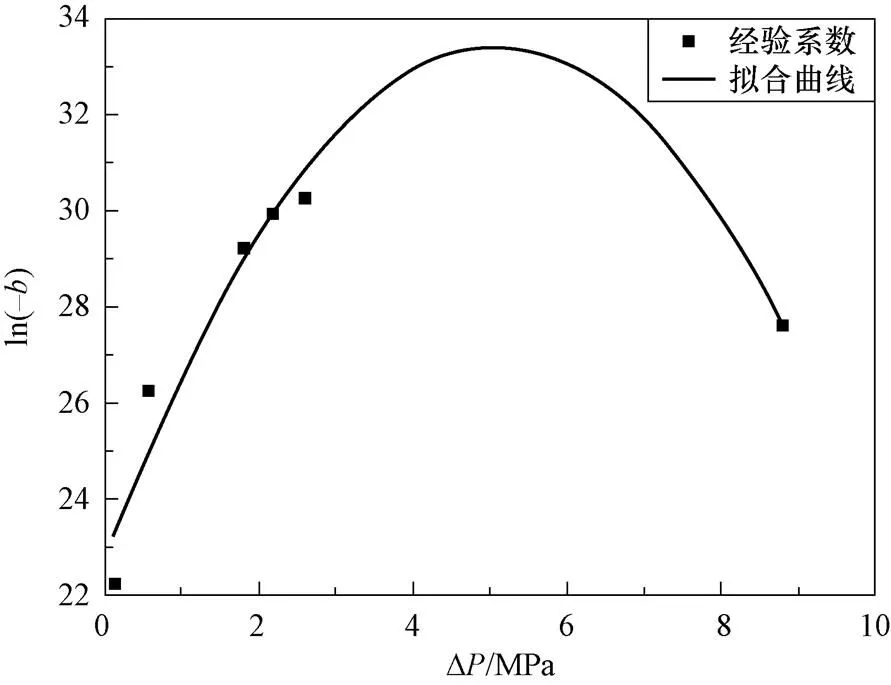
图6 经验系数b的拟合结果
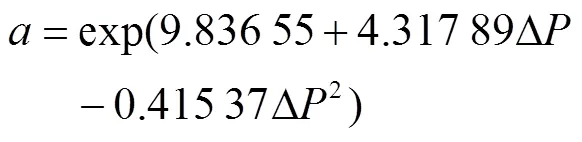
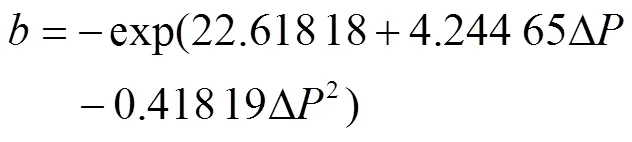
2 钠雾火液滴粒径分布模型的验证
中国原子能院除开展了压差为0.15 MPa下钠液滴粒径分布实验外,为研究250 ℃钠液滴粒径平均直径与喷嘴压差的关系,还分别开展了压差为0.10 MPa及0.05 MPa的实验[11],并得到伴随喷嘴压差的增加,钠液滴的平均直径逐渐减小的结论。下面采用本文所建立的粒径分布模型进行模拟计算,结果如图7所示。可见,伴随喷嘴压差的增加,钠液滴粒径的中位数逐渐减小,峰值粒径的出现概率逐渐增加,与实验结论相一致。
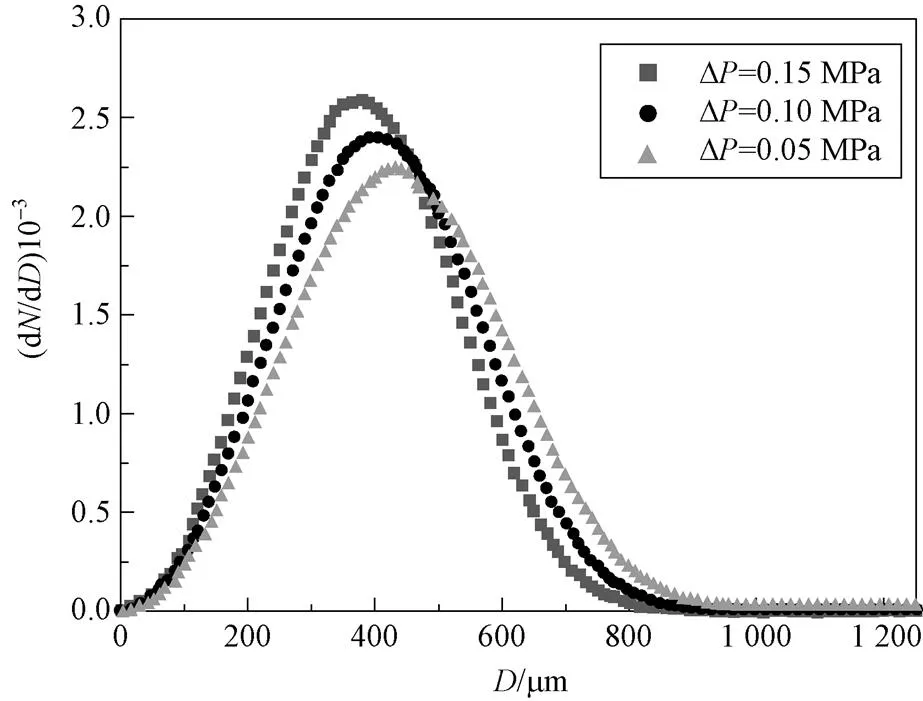
图7 不同压差下钠液滴的粒径分布
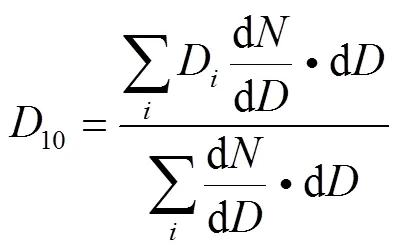
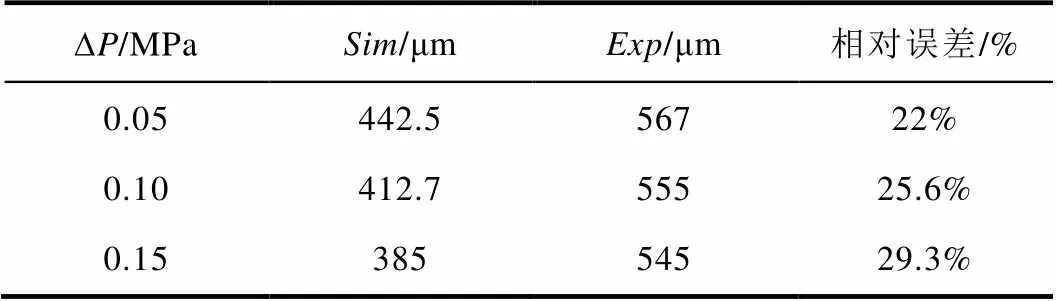
表1 不同压差下钠液滴平均粒径的计算值与实验值的比较
3 总结
本文基于钠雾火事故中在系统内外压差作用下形成的钠喷射雾化现象和最大熵原理建立了以质量守恒方程为主要约束条件的钠液滴粒径分布模型,通过理论推导及实验验证,主要得到以下结论。
(1)该半经验模型可以反映不同压差下的钠液滴粒径分布情况;
(2)该模型经过了钠液滴粒径分布实验验证,预测算数平均粒径的相对误差可以控制在30%以内;
(3)该模型反映出伴随压差的增加,钠液滴的平均粒径逐渐减小。
本研究可为我国自主研发钠火安全分析程序提供模型基础。
[1] 汤烨鑫.钠冷快堆柱状流钠火仿真研究[D].哈尔滨:哈尔滨工程大学,2015.
[2] 彭康玮.钠冷快堆柱状钠火的实验研究[D].哈尔滨:哈尔滨工程大学,2014.
[3] 王国芝,杜海鸥,王荣东,等.钠雾火试验结果及雾火程序计算的比较分析[J].原子能科学技术,2017,51(3):432-438.
[4] TSAI S S.The NACOM code for analysis of postulated sodium spray fires in LMFBRs[R].USA:Brookhaven National Laboratory,1980.
[5] CLARK A J,DENMAN M R.Sodium spray fire simulations using CONTAIN-LMR[R].USA:Sandia National Laboratory,2016.
[6] 王婕.对撞式喷嘴雾化特性的实验研究与数值模拟[D].南京:南京理工大学,2017.
[7] WU Shaohua,LAO Chungyting,AKROYD J,et al.A joint moment projection method and maximum entropy approach for simulation of soot formation and oxidation in diesel engines[J].Applied Energy,2020,258:114083.
[8] LEE K H,LEE C H,LEE C S.An experimental study on the spray behavior and fuel distribution of GDI injectors using the entropy analysis and PIV method[J].Fuel,2004,83:971-980.
[9] 曹建明.喷雾中液滴尺寸和速度概率密度分布函数解的推导[J].西安公路交通大学学报,1996,16(3):75-79.
[10]曹建明,何建,李献国.基于最大熵原理的喷雾液滴尺寸和速度联合分布函数[J].交通运输工程学报,2008,8(5):1-8.
[11] DU Haiou,Wang Rongdong,WANG Guozhi,et al.Sodium spray research in argon atmosphere[R].China:Department of Fast Reactor Research and Design,2014.
[12] MANZINI G,TORSELLO G,PAROZZI F.Sodium safety- spray and pool fires ECART modeling[C].Proceedings of the 2013 15th International Topical Meeting on Nuclear Reactor Thermal-Hydraulics,NURETH-15.Pisa,Italy,May 12-17,2013.
Model Development of Sodium Drop Size Distribution Based on Maximum Entropy Principle
ZOU Wenbin,TONG Lili*,CAO Xuewu
(School of Mechanical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)
The sodium spray fire accident is one of the important objects of fast reactor safety analysis,in which,the drop size distribution formed by injection of molten sodium outward under the pressure drop of the system is one of the key factors affecting the risk level of sodium spary fire accident. In order to predict the drop size distribution during sodium spray fire accident,the sodium drop size distribution model is theoretically derived,with mass equation being treated as the main constraint,based on the maximum entropy principle. Moreover,a semi-empirical formula is obtained by fitting method for convenient application,based on experimental data on the drop size distribution of the atomized fuel and molten sodium,which presents the relation between size distribution and pressure drop. Finally,validations are conducted against experimental data on mean size of sodium drops under different pressure drop obtained from China Institute of Atomic Energy,with relative error being controlled less than 30%. The present model also demonstrates that the mean size of sodium drops decrease with the increase of the pressure drop.
Sodium spray fire;Sodium drop;Drop size distribution;Maximum entropy principle
TL364
A
0258-0918(2022)02-0477-07
2021-03-02
国家自然科学基金资助项目(U1967202)
邹文斌(1998—),男,山东烟台人,博士研究生,现从事核能科学与工程方面研究
佟立丽,E-mail:lltong@sjtu.edu.cn

