空间异形薄壁拱结构极限稳定研究

谢益伟

(益阳市赫山区公路建设养护中心， 湖南 益阳 413002)

0 引言

随着我国桥梁建造水平的提高，钢拱桥已经成为拱桥中一种非常重要的桥型，不同于钢筋混凝土拱桥，采用钢结构的拱桥跨度较大，结构宽跨比较小，截面一般为薄壁形式，在施工及运营过程中均存在失稳的问题。薄壁钢结构拱桥进行失稳分析时，需要考虑3种失稳模态，即：构件局部失稳、整体失稳和整体-局部失稳[1]。随着弹塑性屈曲理论和计算机技术的发展，对薄壁板以及整体结构失稳的研究已经非常成熟，在实际工程中也得到了广泛应用[2]。但是对结构整体或局部构件进行失稳分析时，往往将其割裂开来单独分析，不考虑两者的相互作用。在实际结构中，失稳模态往往呈耦合状态，从目前国内研究现状来看，研究重点大部分集中于拱桥的整体稳定或者单个构件局部稳定上，对于整体-局部稳定研究极少，亟需开展该方面的研究。

一般大跨度钢结构拱桥跨度较大，具有典型的几何非线性效应，加上残余应力、初始变形的影响，具有平衡分支点(第1类)稳定的整体，局部稳定效应几乎不存在，研究第2类稳定更具有实际意义。而第2类稳定问题本质上是一个极限承载力的问题，拱肋作为一种压弯构件，应考虑极限失稳荷载的极值点失稳问题，从而将其转化为一个双重非线性的极限承载力问题[3-5]。目前主要研究领域均集中于结构的线弹性稳定，对于极限稳定的研究不多，相关问题有待解决。

开展该类问题的研究，传统的梁杆单元建模无法模拟局部构件的空间应力，得到的结果并不能够精确地反映结构的极限承载力。大跨度薄壁结构在偏载作用下不可避免地存在翘曲和畸变等局部效应，因此需要建立一个既能反映整体受力，又能反映局部应力分布的的有限元模型。本文基于混合有限元技术，以某大跨径异形拱为研究对象，开展计入结构非线性行为的极限承载力研究，并与传统的空间梁杆单元模型进行对比，得到的结论可为同类型工程的稳定性分析提供参考。

1 工程概况

某大跨径钢箱梁拱桥结构形式为双肢拱肋钢箱梁异形拱，跨径(100+450+100)m，截面为凸形截面，拱肋由上下两肢构成，边跨下肢拱采用二次抛物线，净矢高为4.5 m；主跨下肢拱采用悬链线，矢跨比1/5，拱轴系数1.6；上肢拱采用两端圆曲线和中间二次抛物线组合，中间二次抛物线部分矢跨比为1/11.5。边跨拱肋与中跨拱肋呈1∶5的水平倾斜度布置，拱肋采用Q345钢材。桥型布置见图1。

图1 桥型布置图(单位： m)

2 有限元建模

分析大跨度钢结构拱桥极限承载力，传统的梁杆单元建模无法对空间应力分布进行模拟，而建立全桥实体模型又不太现实，因此本文采用混合有限元技术建立该桥精细化模型。由于板壳单元可以对箱型截面横向应力、剪力滞效应、翘曲及畸变进行模拟，该桥拱顶拱肋部分采用Shell63壳单元模拟，吊杆单元采用三维杆单元Link10模拟，其余横撑、斜撑等构件采用梁单元Beam188模拟，梁单元与壳单元之间使用Cerig命令建立刚域，耦合交点自由度[6]。拱肋有限元模型见图2、图3。

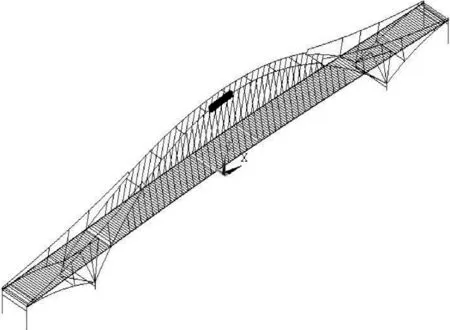
图2 整体有限元模型

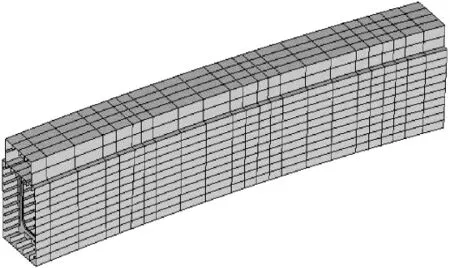
(a) 拱肋壳单元

在开展大跨度钢拱桥稳定性分析时，材料非线性和几何非线性的影响不容忽视，考虑几何和材料双重非线性效应的稳定极限承载力分析更具实际意义。本文根据以往研究成果，在进行极限承载力分析时，考虑了钢材本构关系、初始缺陷、残余应力等影响。

2.1 本构关系

根据相关研究成果，Q345钢材的应力应变曲线关系存在图4中的3种模式。

图4 钢材的3种应力应变简化模式

图4中3种模式在计算具有极值点失稳的构件极限承载力时所得结果误差较小，而模式c相比于模式a、模式b更为简便，因此本文采用模式c。

2.2 初始缺陷

当构件或结构存在初始变形时，其局部或整体变形的幅值会对结构或构件的极限承载力计算产生影响。为计入该影响，本文采用英国BS5400规范确定构件初始变形的幅值，计算公式见式(1)。

(1)

2.3 残余应力

目前，我国对钢箱梁拱桥残余应力的测试几乎没有，本文进行数值分析时，以日本部分钢箱梁斜拉桥的残余应力测试结果为参考，具体见文献[7]。

3 结构稳定极限承载力分析

为研究拱肋的破坏机理，对结构进行极限承载力分析，首先应保证局部壳元模型比其他部分结构先进入破坏阶段。因此需要对局部模型进行极端超加载分析，此处定义超载稳定安全系数λ1和稳定安全储备系数λ2，其对应的加载方式分别为：

超载稳定安全系数：恒载+λ1×活载；

稳定安全储备系数：λ2×(恒载+活载)。

根据以上思路，在λ2×(恒载+活载)的基础上在，局部板壳模型所对应的主梁进行局部汽车超载。结构破坏时的荷载为：

P=λ2×(恒载+活载)+λ3×局部超载

(2)

本文选用对比模型进行极限承载力分析，一种是空间梁杆单元模型，另一种是混合有限元模型(即在拱顶段使用高阶板壳单元代替梁单元)。对比分析2种模型在极限承载力下的应力分布及安全系数。

3.1 梁单元模型

对梁单元模型进行有限元分析，钢材材料本构模型取理想弹塑性模型，E=2.1×105MPa，屈服点取345 MPa。分析时计入初始缺陷及残余应力的影响。根据整体计算结果可知，在2×(恒载+活载)时，结构已经进入弹塑性阶段，在此基础上对跨中拱肋进行局部超载，超载分析至结构刚度矩阵奇异结束。拱顶跨中截面荷载 — 位移曲线见图5。其中时间步1对应2×(恒载+活载)；时间步1以后对应局部超载。最终极限荷载用式(2)表示，求得λ2=2，λ3=14.1。

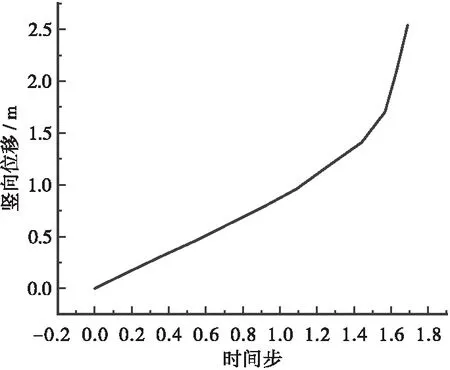
图5 空间梁杆模型加载过程荷载-位移曲线

图6给出了拱肋跨中、拱脚上下肢结合处两处关键截面的VON MISES应力分布结果。由图可知，在局部超载作用下，跨中拱顶位置绝大部分区域达到屈服应力345 MPa，拱顶截面接近全截面屈服，拱脚上下肢结合处位置底板达到屈服应力，截面出现部分屈服，越靠近拱脚，截面屈服面积越小。

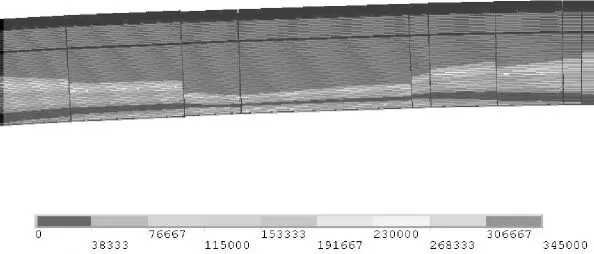
(a)跨中拱肋

3.2 混合单元模型

采用混合单元进行极限承载力分析时，同样采用局部超载的加载方式，当结构刚度矩阵奇异(即结构失效)时，拱顶跨中截面荷载—位移曲线见图7。其中时间步1对应于2×(恒载+活载)；时间步1以后对应于局部超载。最终极限荷载用式(2)表示，求得λ2=2，λ3=11.4。

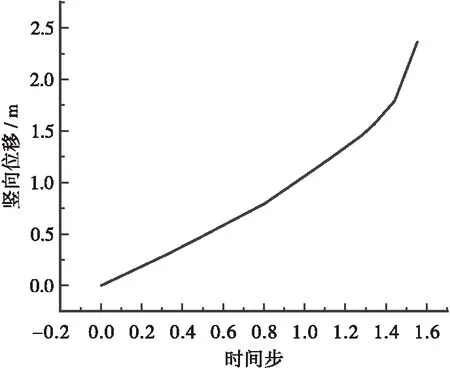
图7 混合模型加载过程荷载-位移曲线

图8给出了混合模型跨中拱肋、横向加劲肋、横隔板以及拱脚上下肢结合段等位置或构件的VON MISES应力分布结果，由图可知，采用混合单元模型分析时，跨中拱肋和拱脚结合段区域应力分布与空间梁杆单元大体相同，但局部存在一定差异。如拱肋跨中位置，受到空间应力的影响，采用高阶板壳单元的混合模型得到的屈服面区域较空间梁杆单元模型大，这是由于薄壁箱型截面存在的畸变、剪力滞效应造成的，而空间梁杆单元无法反映该现象。图8(b)和图8(c)验证了空间效应对极限承载力的影响，横向加劲肋和横隔板顶部位置均达到屈服。拱脚上下肢结合段则位置则没有明显变化。

(a) 跨中拱肋

图9给出了2种模型的荷载 — 位移曲线结果对比，由图可知，在时间步0.5之前，此阶段荷载为1.0×(恒载+活载)，结构处于线弹性工作状态，两者荷载 — 位移曲线基本吻合。此后两者逐渐偏离，随着加载进行，结构逐渐进入塑性阶段，两者结果差异越来越大，最后结构破坏时梁单元模型终止于1.708，混合单元模型终止于1.574。这是由于混合单元法考虑了钢拱肋的局部效应，得到的极限承载力结果较空间梁杆单元低。

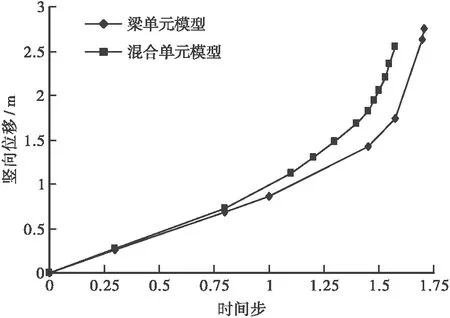
图9 荷载位移曲线对比

4 结论

本文以某钢箱梁拱桥为研究对象，建立了板壳单元混合有限元模型和空间梁杆单元模型，计算了2种模型在极限加载时的超载稳定安全系数及稳定安全储备系数，对比分析了2种模型极限加载时的VON MISES应力分布及荷载 — 位移曲线，可得到以下结论：

1) 采用高阶板壳单元的混合模型既能够反映结构整体受力，又能模拟截面翘曲、畸变等局部效应，在薄壁空间异形结构的极限承载力或极限稳定性分析方面具有明显优势。

2) 局部效应对薄壁空间异形结构的极限稳定或极限承载力有较大影响，以本文工程背景为例，采用空间梁杆单元模型的稳定安全储备系数为14.1，而板壳梁混合模型则为11.4，两者差异达19.15%。混合模型在进行结构极限稳定或极限承载力分析时更为精确，更偏安全。

3) 根据两者的荷载 — 位移曲线结果，在线弹性工作阶段，局部效应对结构影响较小，随着结构进入到弹塑性阶段，局部效应对结构极限承载力的影响开始凸显，最终得到的极限承载力小于传统的空间梁杆模型。