坡顶均布荷载作用下土石混合体边坡的稳定性和破坏特征分析

潘朝晖

(湖南路桥建设集团有限责任公司五分公司， 湖南 长沙 410015)

土石混合体是自然界中广泛存在的一种不连续介质材料，它主要是由一定尺寸的块石、土体和孔隙等组成的多相体系[1]，是一种复杂的工程材料。土石混合体的成因大致可以分为地质风化作用、河流冲积作用、重力堆积作用等，块石的强度和刚度远大于土体，故相较于土质边坡，土石混合体边坡的不均匀性和各向异性较强。一方面，由于形成方式不同，土石混合体可能会有空隙率较大、渗透性较强、强度较弱等特点；另一方面，对于形成条件较好的土石混合体，内部的块石可以形成骨架，从而提高土石混合体的强度和承载力。土石混合体成因和结构复杂，其工程性质因内部因素和外部作用的差异而不同，其中，内部因素主要包括块石级配、含石量、块石形状、表面粗糙度等，外部作用主要包括降雨、外荷载以及其他人类活动等。目前，土石混合体广泛应用于路基填筑、土石坝填筑等方面[2-3]，此外，在我国的西南部分布着大量由滑坡、泥石流和其他地质作用而形成的土石混合体边坡，这些土石混合体边坡的安全性对当地人民的生产生活有着重要影响。因此对土石混合体边坡的稳定性和破坏特性展开研究具有重要的现实意义。

目前，关于土石混合体的研究主要有试验研究和数值模拟两种方法。在试验研究方面，以大型原位试验为主。宋岳等[4]对三峡库区的土石混合体进行原位剪切试验，得到了土石混合体的应力-应变曲线并就其变化规律进行了分析；孙韬等[3]通过大型直剪试验，研究了块石含量对无黏性土石混合体抗剪强度的影响；Zhang等[5]对在黏性土中掺入块石形成土石混合的土石坝心墙材料进行大型击实试验和原位直剪试验，研究了土壤和土石混合料的力学行为差异；Liu等[6]通过直剪试验，对土石混合体剪切“跳变”现象进行了研究。在边坡稳定性分析计算方面，传统的方法主要是极限分析法，即先假设边坡滑裂面的存在，然后对滑裂面之上的土体进行极限平衡分析，这种方法对于均质的各向同性土体具有优越性。但研究表明，土体的各向异性会对边坡稳定性产生一定程度的影响[7]。因此，利用数值模拟软件进行计算分析成为了目前土石混合体边坡稳定性分析的主要形式。数值模拟一般要首先建立土石混合体模型，然后导入到数值分析软件进行计算。徐文杰等[1]通过土石混合体的大尺度直剪试验数值模拟，提出了土石混合体内部塑性区扩展的3种形式；成浩等[8]运用离散元分析的方法，研究了含石量和坡度对土石混合体边坡崩塌运动规律的影响；刘顺青等[9]利用有限元软件分析了不同含石率和基覆岩层倾角下土石混合体边坡的稳定性。

在以往的工作中，无论是采用离散元方法，还是有限元方法，在对土石混合体边坡进行分析时，都只考虑了边坡在自重作用下的稳定性，而在实际工程运用中，仅仅考虑自重是不够的。有时为了满足生产和生活的需要，需要在边坡之上修建一些建筑物，此时边坡除了自重之外，还承受了外荷载作用，往往人为施工是造成大多数斜坡滑塌的重要原因之一[10]。作为一种高度不均匀、各向异性的材料，土石混合体边坡在承受外荷载作用时，其在内部应力应变、位移以及破坏模式上必然与均质边坡有差异。本文在总结以往研究的基础上，建立了不同含石量的边坡模型，利用ABAQUS有限元软件对不同边坡在受到不同外界荷载作用时的稳定性和破坏特性进行研究。

1 模型建立

1.1 块石模型建立

生成块石颗粒是建立土石混合体边坡模型的第一步，为了尽可能保持天然石块形状的随机性和多样性，目前比较流行的建模方法主要有两种：一种是基于相关理论构建颗粒轮廓，通过编写程序，建立一系列纯数字化的块石轮廓信息[9， 11]，此种方法建立的块石模型往往与自然条件形成的块石有较大差异；另一种是通过对野外真实块石进行拍照或扫描，并对图像进行处理，从而得到真实形状的块石模型[1， 11]，本文采用此方法，块石图像的处理过程见文献[12]。本文基于MATLAB平台，编写了一套块石随机投放的程序，首先输入块石的级配、边坡含石量等信息，然后程序从块石数据库中随机选取块石，对其进行适当缩放，并将块石随机投放到边坡区域内，每次投放都进行块石相交性判断，直至边坡达到相应的含石量，块石的具体投放过程见文献[11]。扫描的块石经MATLAB进行处理后，保存的文件类型为包含有块石轮廓坐标的txt文本文件，这类文件无法被ABAQUS识别，因此需要将其进一步转换。本文利用AutoCAD软件，将txt中所有坐标值复制进CAD的命令框，CAD根据坐标数据，自动绘出所有块石的轮廓，然后将这些块石轮廓线输出为ABAQUS可识别的igs文件并将其作为部件导入ABAQUS软件进行建模及计算分析。本文共建立4个不同含石量的边坡模型，含石量分别为0、20%、40%、60%，同时，在每个边坡模型的顶部施加均布线荷载q，荷载大小分别为0、20、50、70、100 kN/m，探究土石混合体边坡在承受坡顶均布荷载时的受力特性和破坏模式。模型尺寸和荷载分布情况如图1所示，其中边坡尺寸见图1(a)。3个土石混合体边坡内块石均采用同一级配，级配曲线如图2所示。

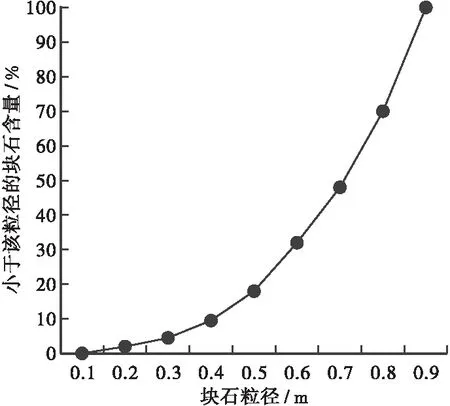
图2 块石级配曲线

1.2 模型信息

采用ABAQUS有限元软件对上述4个模型分别进行不同荷载下的稳定性计算，其中材料参数如表1所示，通过设置随场变量线性变化的土体参数实现强度折减，初始场变量设置为0.5，终止场变量为2.0，具体过程如表2所示，土石混合体中，块石的强度要远远高于土体，边坡的破坏也仅发生在土体内部和土-石界面处，形成“绕石效应”，因此，计算过程中仅对土体参数进行折减。土石混合体中，土体和块石相交的界面在进行强度折减过程中，可能出现分离、滑移等情况，为了使数值模拟更加符合实际情况，本文在土-石界面设置了通用接触。通用接触是ABAQUS内置的一种接触方式，它能够自动搜索界面的接触和分离现象，在存在多个接触面或者接触面形状复杂的模型中，具有良好的适用性，在本文的通用接触参数设置中，土体和块石之间切向采用罚函数定义摩擦，摩擦系数为0.5，法向采用硬接触。网格类型采用CPE4(4结点双线性平面应变4边形单元)。

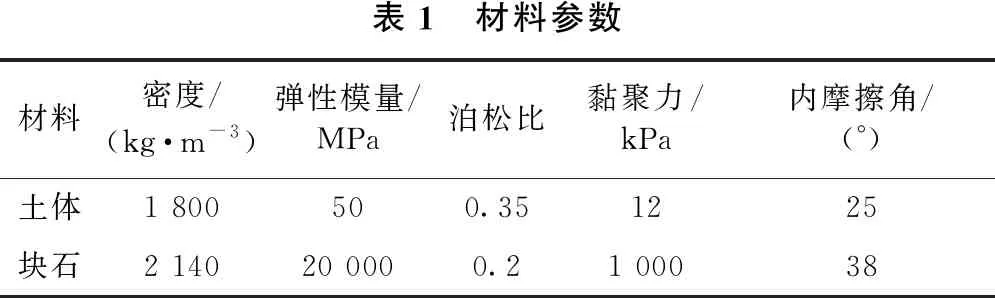
表1 材料参数材料密度/(kg·m-3)弹性模量/MPa泊松比黏聚力/kPa内摩擦角/(°)土体1 800500.351225块石2 14020 0000.21 00038

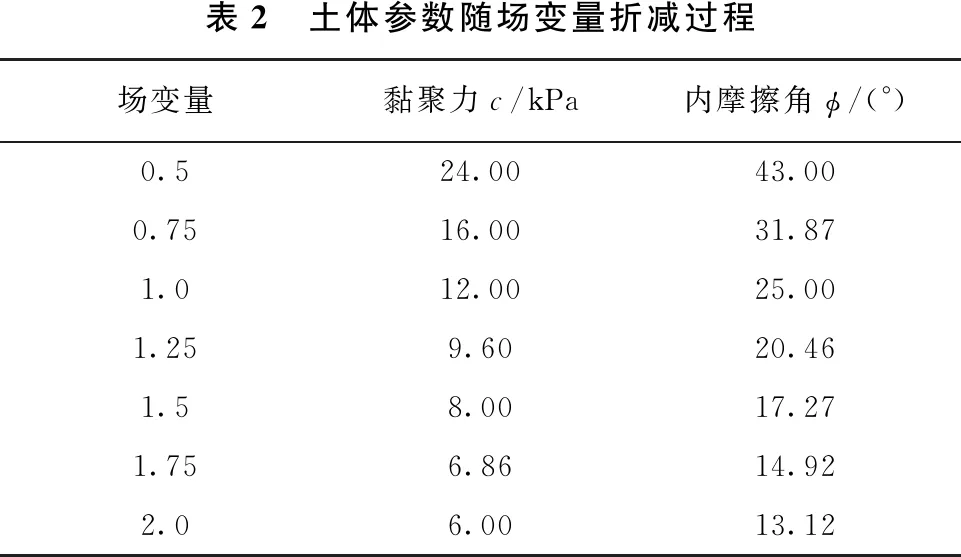
表2 土体参数随场变量折减过程场变量黏聚力c/kPa内摩擦角ϕ/(°)0.524.0043.000.7516.0031.871.012.0025.001.259.6020.461.58.0017.271.756.8614.922.06.0013.12

2 模型计算

边坡安全系数采用强度折减法，屈服准则采用Mohr-Coulomb准则。

2.1 强度折减法

强度折减法是Zienkiewicz等[13]于1975年提出的，其实现方法是在进行有限元计算过程中，保持荷载不变，将土体的抗剪强度参数(c和φ)值同时除以一个折减系数(Fr)，对边坡抗剪强度进行折减，并将折减后的土体抗剪参数(cm、φm)代入有限元进行计算。如此循环往复，随着折减系数Fr增大，土体所能产生的抗剪力越来越小；当土体内部产生的抗剪力小于荷载引起的剪应力时，边坡就会失稳，此时的折减系数(Frmax)就是边坡的安全系数。材料折减过程如式(1)所示。

(1)

2.2 屈服准则

大量试验结果表明，Mohr-Coulomb准则符合岩土材料的屈服和破坏特征，因此，Mohr-Coulomb准则也被大量运用于岩土体的边坡稳定性分析中。本文所采用的理想弹塑性模型及Mohr-Coulomb破坏准则可以表示为式(2)。传统的Mohr-Coulomb模型主应力是一个不规则的6面体，屈服面存在尖角，易造成计算缓慢和不收敛等情况，因此,在ABAQUS中，Mohr-Coulomb模型采用光滑流动势函数[14]，使其偏应力空间无拐角，塑性流动方向唯一。

(2)

式中:I1、J2为应力张量的第1不变量和应力偏张量的第2不变量；θe为应力Lode角。

2.3 安全系数的确定

安全系数是评价边坡稳定性的重要指标，但目前在边坡有限元计算安全系数的确定问题上，学界尚无定论，主要有3种争议存在。栾茂田等[15]认为滑移面塑性应变区贯通时，其上每一点都达到了极限平衡状态，因此，可以将广义塑性应变分布和其发展状态作为边坡失稳的判断依据；赵尚毅等[16]认为塑性区贯通是边坡失稳的必要而非充分条件，将有限元计算是否收敛作为边坡失稳的判断依据更为合理；刘金龙等[17]认为有限元计算是否收敛受到分析步、网格划分等多种因素影响，以此作为边坡失稳判断依据将产生较大误差，因此,推荐以边坡特征点位移突变作为边坡失稳的判断依据。基于ABAQUS软件强大的后处理能力，本文分别以主流的3种方式确定边坡的安全系数，并加以对比分析。

3 结果分析

在本节中，将对本文建立的4个不同含石量边坡模型在不同均布线荷载作用下的应力分布、位移分布、塑性应变、安全系数等方面进行对比分析，以探究块石含量和外荷载作用对边坡稳定性的影响。

3.1 应力分布

不同含石量边坡在坡顶受到100 kN/m的均布荷载作用时，内部的应力分布见图3。从图3中可以看出，由于均质土坡内部材料均匀，各向同性，因此，受到外荷载作用时，内部应力分布均匀变化，有规律可循。随着土坡内部含石量增加，土体内部材料的不均匀性增加，块石骨架逐渐形成，其内部应力重分布，主要承受结构由土体逐渐转变为块石，应力分布明显沿着块石骨架形成一条高应力的通路，块石周围土体土体承受的应力明显减小，含石量越高、所受的外荷载越大，边坡内部的沿块石分布的应力带越明显。

图3 100 kN/m荷载下不同含石量边坡应力分布

3.2 位移分布

位移场的分布情况是边坡有限元分析的重要结果之一。通过位移的分布情况，既可以看出边坡的潜在滑裂面，也可以得到边坡可能存在的破坏方式以及崩塌体积等情况(见图4、图5)。从图 4和图5可以看出，均质边坡的潜在滑裂面为光滑的弧形，且通过坡脚。随着含石量和外荷载增加，滑裂面逐渐向上移动且形状不规则，滑坡体的体积随着外荷载和含石量增加而减小。这提示我们，在实际工程中，当土石混合体边坡上存在超载时，要特别注意坡顶处的加固，防止发生崩塌、落石等现象。

(a) 无荷载

3.3 塑性应变

塑性应变的发展情况也是边坡稳定性分析中的关注重点，通过塑性应变区分布情况，可以找到边坡的潜在滑裂面，并基于此开展边坡的支护和加固工程。图 6、图7分别是相同含石量(40%)边坡的塑性应变在不同荷载作用下的分布情况以及相同荷载(50 kN/m)下不同含石量边坡的塑性应变分布情况。需要指出的是，均质土坡由于其承载能力较低，在50 kN/m的荷载作用下，产生了二次滑裂面，而在20 kN/m荷载作用下，塑性应变区仍旧是一条通过坡脚的光滑弧线；土石混合体边坡由于其承载能力较高，并没有出现二次滑裂面。随着含石量和荷载的增加，塑性应变区由从坡脚至坡顶贯通逐渐转变为部分贯通，剪切带形状也更为破碎和不规则，塑性应变区范围逐渐减小。当含石量为60%时，塑性应变只在少数几个小范围区域内才能观察到，此时，运用塑性应变区发展状况作为边坡失稳的判断依据时，人的主观因素较大，可能会带来较大的误差。在塑性应变发展过程中，表现出明显的“绕石效应”，且在不同荷载作用下，绕石路径也不同；在较低荷载作用下，绕石路径为单向绕石，只产生一条塑性应变带；在高荷载作用下，绕石方向为双向，产生了多条塑性应变带，这也是土石混合体边坡剪切带更为破碎的原因。

(a) 无荷载

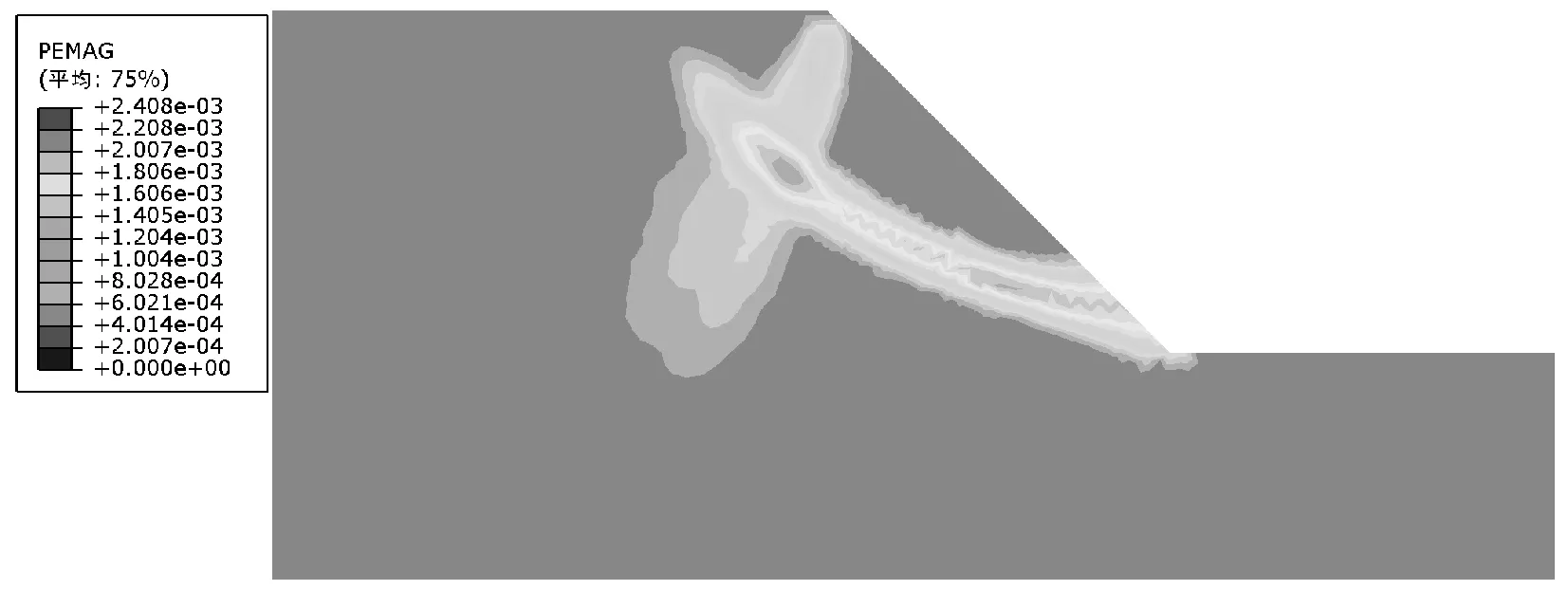
(a) 均质土坡

3.4 安全系数

安全系数是判断边坡稳定性和安全性的重要依据，一般来说，安全系数越大意味着边坡的稳定性和安全性越高，但在实际有限元计算过程中，采用不同边坡失稳判断依据，计算所得到的安全系数大小也不同。因此，本文从数值计算不收敛(准则一)、特征点位移突变(准则二)和塑性应变区贯通及其发展(准则三)3个方面分别计算不同含石量边坡在不同荷载作用下的安全系数，结果分别如表 3、表4和表5所示。

表3、表4和表5分别展示了在目前边坡失稳判断的3个准则下，本文所建立的4个不同含石量边坡模型在5种不同大小荷载作用下的安全系数。从表中可以看出： ①在无外荷载或者外荷载较低的情况下，随着边坡含石量增加，边坡的安全系数逐渐增大，块石的存在提升了边坡稳定性。这是因为随着含石量增加，边坡滑裂面形状越来越不规则，“绕石效应”越来越明显，块石对滑坡体的下滑趋势有延缓作用。②在较高荷载作用下，随着边坡含石量增加，边坡安全系数出现先增大后减小现象；这是因为随着含石量和荷载增加，边坡滑裂面逐渐上移，裂带长度减小，滑裂面上方土体中的块石增加了土体重力，此时裂带减小，其“绕石效应”而产生的抗滑力不足以抵消滑坡体中块石增加的下滑力，所以安全系数降低。③以数值计算是否收敛作为边坡失稳判断准则计算所得的安全系数，要大于位移突变和塑性应变区贯通作为判断准则计算所得的安全系数；另外3.3节中也提到，在土石混合体边坡中，随含石量和荷载增加，剪切带越来越破碎，塑性应变区变化不明显，以此作为边坡失稳判断依据，则会产生较大的主观误差；因此，本文提出以边坡坡顶点位移突变作为土石混合体边坡失稳判断准则更为合理。

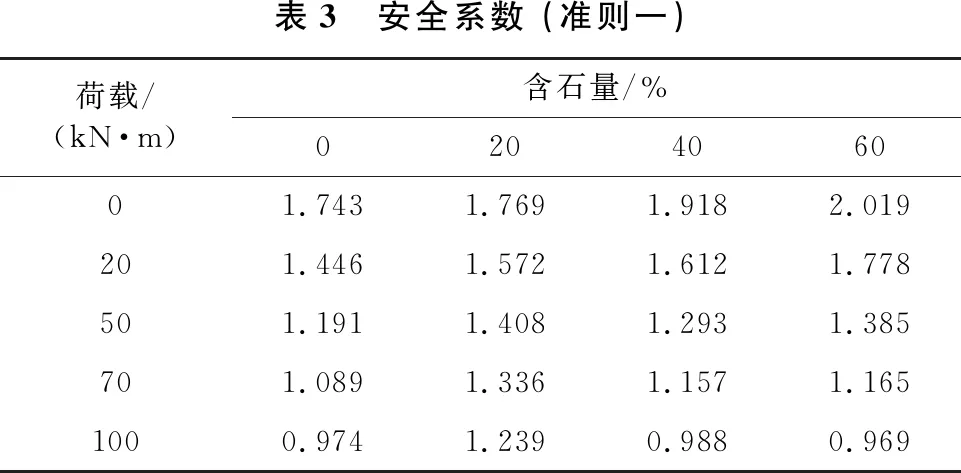
表3 安全系数 (准则一)荷载/(kN·m)含石量/%020406001.7431.7691.9182.019201.4461.5721.6121.778501.1911.4081.2931.385701.0891.3361.1571.1651000.9741.2390.9880.969

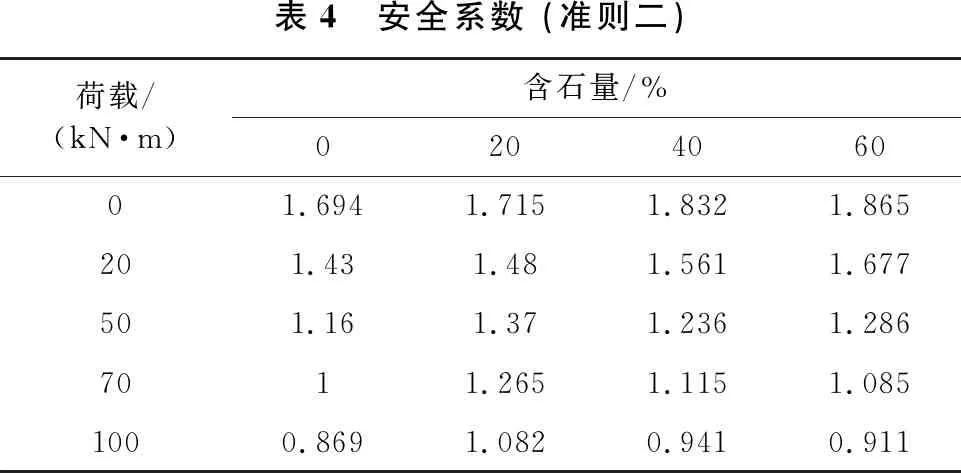
表4 安全系数 (准则二)荷载/(kN·m)含石量/%020406001.6941.7151.8321.865201.431.481.5611.677501.161.371.2361.2867011.2651.1151.0851000.8691.0820.9410.911

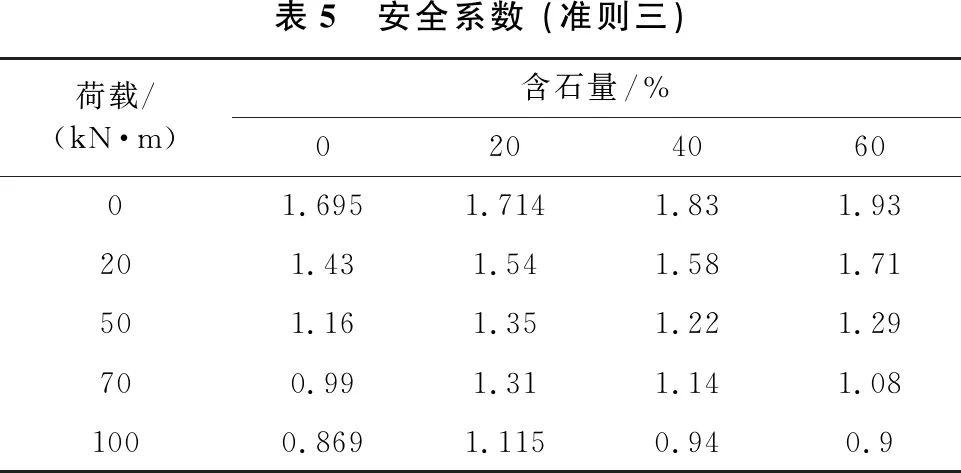
表5 安全系数 (准则三)荷载/(kN·m)含石量/%020406001.6951.7141.831.93201.431.541.581.71501.161.351.221.29700.991.311.141.081000.8691.1150.940.9

4 结语

1) 土石混合体内块石的存在会改变边坡内部应力场的分布情况，随着块石含量增加，改变作用更加明显。具体表现为块石会产生骨架作用，从而承受大部分应力，沿块石骨架形成明显的高应力带，且含石量和外荷载增加，高应力带越明显。

2) 均质土坡的潜在滑裂面通过坡脚，随着含石量以及外荷载增加，滑裂面逐渐上移，滑坡体体积减小，边坡破坏形式存在由滑坡向崩塌转变趋势，在高含石量和高荷载地区，要注意坡顶土石体的支护与加固。

3) 土石混合体边坡的安全性与含石量及外荷载大小有关。在较低荷载作用下，随着含石量增加，安全系数逐渐增大；在较高荷载作用下，随着含石量增加，边坡的安全系数呈现出先增大后减小趋势，这与不同含石量和荷载作用下边坡的破坏特性有关。

4) 土石混合体边坡的破坏特性与含石量和外荷载大小有关。随着含石量和外荷载增加，边坡滑裂面位置逐渐上移，滑裂带长度减小，“绕石效应”所增加的抗滑力不足以平衡滑坡体中块石重力所附加的下滑力，导致安全系数减小。

5) 在边坡失稳3种判断依据中，数值计算不收敛时，边坡实际上已经产生无穷大位移导致失稳，因此数值偏大；而土石混合体边坡的塑性应变发展过程复杂，难以判别，故本文推荐以边坡特征点位移是否发生突变作为土石混合体边坡是否失稳的判断准则。