三类几何概型概率的求法
冯东新



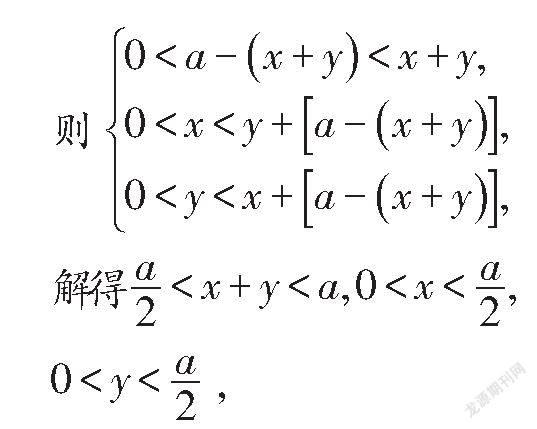
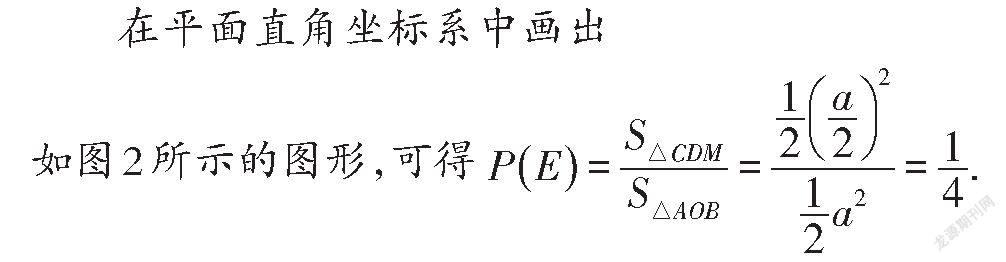
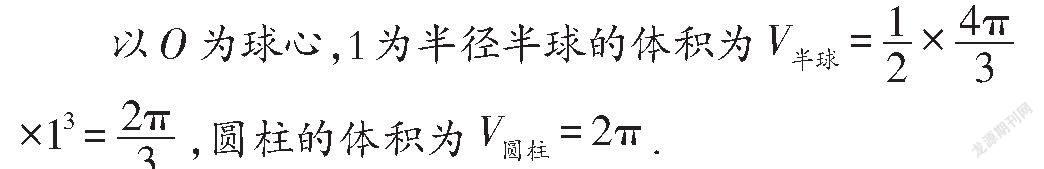

一、与长度有关的几何概型
对于与线段长、边长、距离有关的概率问题,其试验的结果所构成的区域均可用长度表示,只需分别求出事件所构成的区域长度与实验的全部结果所构成的区域长度,再根据几何概型的概率公式进行求解.
例1.某公共汽车站每隔15分钟有一辆汽车到达,乘客到达车站的时刻是任意的.求一位乘客到达车站后等车时间超过10分钟的概率.
分析:从前一班车出发的时间算起,每位乘客到达该车站的时刻t可以是0-15分钟中的任意一个时间点,并且每一位乘客到达该车站是等可能的,因此该问题属于几何概型.构成事件的结果可用长度表示,所以可运用几何概型的概率公式来求解.
解:设上一辆车于T时刻到达,下一辆车于T時刻到达,则线段TT的长度为15.设T是线段TT上的点,且TT=5,TT=10,如图1所示.
二、与面积有关的几何概型
与面积有关的几何概型,主要是与三角形、矩形、圆等平面图形的面积有关的概率问题.解答该类问题的关键是判断事件所构成的区域是否与面积有关,然后根据几何概型的概率公式进行计算.
例2.在长度为a的线段内任取两点,将其分为三段,求它们可以构成一个三角形的概率.
解:记“长度为a的线段随机分成三段,将其分成
三段”为事件E,
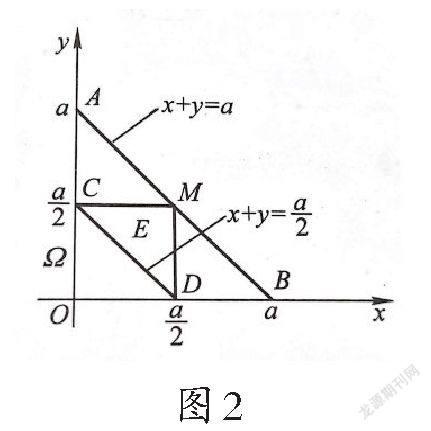
由于在长度为a的线段内所取的两点是任意的,且两点互不影响,所以点(x,y)落在△AOB内的任意一个位置都是等可能的,故该问题属于几何概型,且事件所构成的区域可用面积表示,求得△CDM,△AOB的面积即可解题.
三、与体积有关的几何概型
对于与体积有关的几何概型问题,常见的有与三棱锥、棱柱、圆锥、圆锥、长方体、正方体、球的空间几何体的体积有关的问题.在解题时,需先判断出实验的结果构成的区域是否与几何体的体积有关,然后运用几何概型概率公式解题.
例3.有一个底面圆的半径为1、高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,求点P到点O的距离大于1的概率.
分析:P是圆柱内任意一点,所以事件所构成的区域需用体积来表示,分别求得点P到点O的距离等于1的半球的体积、圆柱的体积,便可运用几何概型的概率公式解题.
解:记“点P到点O的距离大于1”为事件A,
由几何概型的概率公式得:
可见,求解与长度、面积或体积有关的几何概型问题,首先要确定试验的结果所构成的区域是否可用长度、面积、体积表示,然后求得事件所构成的区域的长度、面积、体积,以及所有结果构成的区域长度、面积、体积,最后根据几何概型的概率公式求解.

