教育对健康的分布处理效应——基于断点回归设计

李青原

(中国社会科学院大学 人口与劳动经济系， 北京 102488)

一、引言

教育与健康之间是否存在因果关系，一直以来受到国内外学者的广泛讨论。[1]究其原因：一是教育与健康作为人力资本的重要组成部分，是各国经济和社会发展的政策着力点，而教育与健康的交互影响，将使得教育投资具有双重效应，这为人力资本投资战略的调整和发展提供方向；[2]二是教育对健康可能存在的积极作用，有助于应对人口老龄化带来的挑战。[3]另外，营养和健康本身也是重要课题，[4][5]党的“十九大”报告提出的“健康中国战略”意味着人民健康已成为中国国家战略问题，探究影响健康的因素是应有之义，因而，教育对健康的因果推断具有重要的现实意义。

关于教育与健康的因果分析，学界已经进行了一些有益的探索，但是研究结论存在差异。[6]部分研究认为，教育对健康有显著的正向影响，[7]然而，还有一些学者却发现，教育对健康基本没有影响或两者不存在因果关系。[8][9]国内的相关研究基本上认为教育在一定程度上有助于改善健康水平，但在受益群体和作用大小上存在不同的看法和结论。比如，程令国等(2014)与叶晓梅和梁文艳(2017)利用中国老年健康影响因素跟踪调查数据(CLHLS)研究发现，教育对中国老年人的身体健康和认知健康产生了积极影响；[2][10]而刘生龙(2017)基于2005年全国1%人口抽样调查数据分析发现，教育只对中国老年男性的健康有显著影响。[3]李春青和王骏(2017)基于中国家庭追踪调查数据(CFPS)，得到教育对女性和农村人口的健康影响较大，对高学历和出生较晚人口的影响较小；[11]而李军和刘生龙(2019)利用CFPS数据，得到教育与男性的自评健康之间存在因果关系，与女性保持正常体型也存在因果关系。[12]可以发现，多数学者主要通过分组研究验证了教育对部分人群的健康存在因果效应，但未得到一致结论。这在一定程度上也表明教育对健康的影响可能“因人而异”，而现有的研究仍未对此进行充分讨论。

从研究方法来看，由于存在教育变量内生的问题，[13]多数研究以义务教育法这类政策变量作为工具变量，使用2SLS估计了教育对健康的因果效应；[14][15]一些研究则利用双胞胎数据，使用固定效应模型对教育与健康的因果关系进行分析。[16]随着实验方法在社会科学研究中的应用，准实验(quasi-experiment)为探究教育对健康的因果效应提供了新思路，而断点回归设计(RDD)作为一种接近自然实验的方法受到了学者们的青睐。一些研究利用义务教育法、自然事件等对教育的外生冲击，基于RDD框架估计了教育对健康的影响。[12]

研究结论之所以存在上述矛盾或差异，一个关键因素在于，无论使用何种因果推断方法，或是按照何种方式将样本分组，现有研究主要分析的是教育对健康的平均处理效应(ATE)，鲜有探究教育对健康的分布处理效应(DTE)，即教育对健康不同分布位置的影响。Galama等(2018)认为，由于异质性的存在，平均影响可能掩盖了教育对健康分布特定位置的显著影响，从而得到看似矛盾或不显著的结论。[17]因此，仅以平均效应为依据，可能会忽略教育对健康的真实影响，从而遗漏一些重要的发现和结论。那么，教育对健康是否存在显著的因果效应，其对健康有何异质性影响？

本文的目的在于回答以上问题。如果教育对健康分布不同位置的影响不同，则教育对健康的影响必然因人而异。因此，本文将基于RDD框架，以义务教育法为工具变量，使用分布检验方法探究教育对健康分布的影响，并与教育对健康的平均影响作比较。本文的贡献主要有两点：一是通过将RDD与分布检验方法相结合，估计教育对健康的分布处理效应，对教育与健康之间的因果关系进行更加准确地推断；二是充分研究教育对健康的异质性影响，探索健康分布不同位置的人如何受益于教育，以得到更多有益的结论，对现有的相关研究进行补充。

二、制度背景与数据

(一)义务教育法的实施和影响

义务教育法的实施对教育可得性产生了外生冲击，为本研究提供了一个良好的政策工具。为了提高国民整体的教育水平，1986年4月12日，《中华人民共和国义务教育法》(简称《义务教育法》)通过，并于1986年7月1日开始执行。诸多研究对该法案进行了较为详尽的阐释，[12]本研究仅对其在实施中的主要特点进行以下说明。

首先，由于中小学一般每年9月1日开学，因而义务教育法实际上于1986年9月1日正式生效。其次，由于地区经济、教育等发展水平的差异，中国各省份实施义务教育法的具体时间并不一致，贫困地区尤其缺乏实施义务教育的资源和能力。[18]根据Huang(2015)的研究，义务教育法的实施年份主要集中在1986和1987年，少数省份的实施时间为1988、1989或1991年。[19]再次，义务教育法对6～15岁人群均有按规定接受义务教育的要求，在义务教育法正式实施时，未满15岁的人群均会受到该法案的影响。为了便于研究，本文将刚好受到该法案影响的人的出生日期作为临界点。最后，并非所有的适龄人群都完成了义务教育，在2006年修订义务教育法之前，仍存在许多因经济负担而辍学的儿童。[20]

可以发现，义务教育法的实施提高了人们的受教育水平。如图1所示，在义务教育法的影响下，受教育水平在临界点处出现了明显的断点(1)图1利用中国家庭追踪调查数据，对样本点进行了多项式拟合，其中，出生日期使用样本出生年月相对于临界点的月数衡量，该图旨在直观地呈现义务教育法实施前后的教育断点，后文将对处理效应进行估计和检验。，与未受到义务教育法影响的群体相比，受到该法案影响的群体其接受义务教育的概率和平均受教育年限均明显提高。然而在临界点处，接受义务教育的概率未达到1，平均受教育年限也并未提高至9年，表明确实存在大量未按规定接受义务教育的群体。

图1 义务教育法实施前后的教育断点

同样地，在义务教育法的影响下，健康水平在出生日期临界点处也出现了断点，换言之，人们的受教育水平可能影响了其健康水平(2)本文同样对样本的健康水平随出生日期的变化进行了多项式拟合，限于篇幅，此处不再展示相关结果。。实际上，在受教育水平整体提升的同时，人们的健康水平也明显上升，具体反映为中国人均预期寿命不断上升。根据国家统计局数据，1981年中国人均预期寿命为67.8岁，2018年中国人均预期寿命已提高至77.0岁。作为广义的人力资本，教育和健康是发展的基本目标，而两者的同步增长也表明，教育与健康之间可能存在因果关系，教育水平的提高可能会导致健康水平的提高。

(二)数据来源与样本选择

研究数据来源于中国家庭追踪调查(CFPS)中2010、2014和2018年的调查数据。该调查由北京大学中国社会科学调查中心(ISSS)实施，CFPS样本覆盖全国25个省、直辖市和自治区，代表了中国94.5%的人口，样本的代表性为研究的外部有效性提供了数据基础。CFPS采用了内隐分层、多阶段、多层次、与人口规模成比例的概率抽样方式，以及计算机辅助面访调查(CAPI)和计算机辅助电访调查(CATI)技术，在一定程度上保证了数据质量。

本研究将在断点回归设计(RDD)的框架下展开，需要对样本范围进行设定。由前文可知，对于1986年开始实施的义务教育法，出生于1971年9月及之后的人群会受其影响。考虑到不同地区义务教育法的生效时间存在差别，因此，本研究以法案生效时年龄为15岁设定临界点。由于中国在1959～1961年经历了严重的饥荒，该自然灾害对教育和健康产生了较大的不利影响，因此，本研究所用样本为出生于临界点前后各9年的群体。在对连续变量的异常值进行处理后，得到的样本量为14338人，其中，男性7145人，占比49.8%，女性7193人，占比50.2%。

(三)变量设置

1.被解释变量

许多研究使用自评健康来衡量身体健康水平，[3]也有研究使用多种指标从身体功能健康、认知功能健康等多个维度衡量健康水平，[10]但有研究认为主观评价与客观评价之间的差异会随着社会经济地位的不同而变化，[21]并且，由于本文重点探讨教育对健康分布的影响，因此，本文使用连续的、客观的指标衡量健康水平(health)，包括身体质量指数BMI、医疗费用和认知功能。

BMI反映了个体的体型和营养状况(3)BMI=体重(kg)/身高(m)2。一般认为，中国成年人的BMI小于18.5为偏瘦，处于18.5～23.9为正常，大于等于24为超重，大于等于28为肥胖。结合样本BMI的中位数(22.5)、均值(22.8)和分布情况，BMI从低分位点到高分位点的变化，即代表了样本从偏瘦到正常、再到肥胖的变化。，在一定程度上代表了个体的身体健康水平。由于个体是否患病以及疾病严重程度难以从BMI中完全反映出来，因此，以医疗费用(medical)指标反映个体的患病情况(一般为身体疾病)，使用个体上一年的住院总费用(包含医保报销)作为医疗费用的代理变量，与BMI共同衡量个体的身体健康状况。认知功能使用识字水平(word)和数学水平(math)衡量，CFPS2010、CFPS2014和CFPS2018主要使用识字题和数学题测试个体的认知水平，两项测试得分区间分别为[0，34]和[0，24]，得分越高代表认知功能越强。为了便于分析和比较，本研究按照性别对所有健康指标进行了标准化处理。

2.解释变量

核心解释变量为教育水平(educ)，用是否完成义务教育(educ9)衡量。同时，设置是否完成高中教育(high)、是否完成大学教育(college)以进行比较分析。驱动变量为出生日期(date)，使用样本出生年月相对于临界点的月数衡量，临界点处的date取值为0。

在RDD的相关研究中，对于是否应加入控制变量并未得到一致结论。本研究设定了控制变量，以与基准回归做比较。控制变量X主要为性别(male)、民族(ethnicity)、婚姻(marriage)和户籍(urban)这些反映个体特征的虚拟变量，分别设定如下：男性取值为1，女性取值为0；汉族取值为1，其他民族取值为0；已婚取值为1，其他婚姻状况取值为0；城镇取值为1；农村取值为0。另外，为了控制地区层面的影响，按照义务教育法实施年份设置地区虚拟变量(dumregion)。

3.工具变量

以义务教育法(CSL)为工具变量，若个体受到义务教育法的影响，则CSL取值为1，否则取值为0。如前所述，义务教育法的实施可视为一种随机实验，按照“是否受到义务教育法影响”对样本随机分组，样本是否受到政策干预取决于其出生日期，与可观测到的个人其他特征以及无法观测到的因素无关。然而，这其中仍存在自选择问题，受到义务教育法影响的个体仍可能未完成义务教育(如图1所示)，后文实证研究将对此进行处理。主要变量的描述性统计结果见表1。

三、教育对健康的平均处理效应

(一)义务教育法对教育的影响

由于并非所有适龄人群都完成了义务教育，因此，本研究采用模糊断点回归(FRDD)。参考FRDD相关研究，[22]本研究以义务教育法为工具变量，使用两阶段最小二乘法(2SLS)进行估计，第一阶段估计义务教育法对接受教育的影响，第二阶段估计教育对健康的平均处理效应。第一阶段使用的模型如下：

表1主要变量的描述性统计分析

educi=α0+α1CSLi+f(datei)+X′iα2+εi

(1)

式(1)中，educi为个体i的受教育水平；CSLi为个体i是否受到义务教育法的影响；datei为个体i的出生日期变量；f(·)为低阶多项式，刻画了受教育水平随出生日期的变化趋势；Xi为控制变量向量，包括所有前定变量以及地区虚拟变量；εi为随机扰动项。

为了得到更加准确的估计结果，第一，根据Gelman和Imbens(2014)的研究，将驱动变量多项式f(·)设定为二阶多项式；[23]第二，根据Calonico等(2014)提出的数据驱动(data-driven)方法得到最优带宽，以提高估计的精准度；[24]第三，回归分析中使用稳健标准误，以避免异方差对估计结果的影响。

第一阶段的估计结果如表2所示。与现有的相关研究和经验认识一致，义务教育法的实施使个体接受义务教育的概率显著提高了5.3%，在加入控制变量后，这一影响下降至4%，但仍在1%的水平上统计显著。考虑到样本中完成义务教育的比例为54.6%，4%～5.3%的影响仍不容忽视。另外，义务教育法主要对个体完成义务教育产生积极作用，对完成高中和大学教育则没有显著影响。实际上，仅有约22%的样本完成了高中教育，仍有约45%的样本未能完成义务教育，因此，义务教育法对于提升整体受教育水平意义重大。

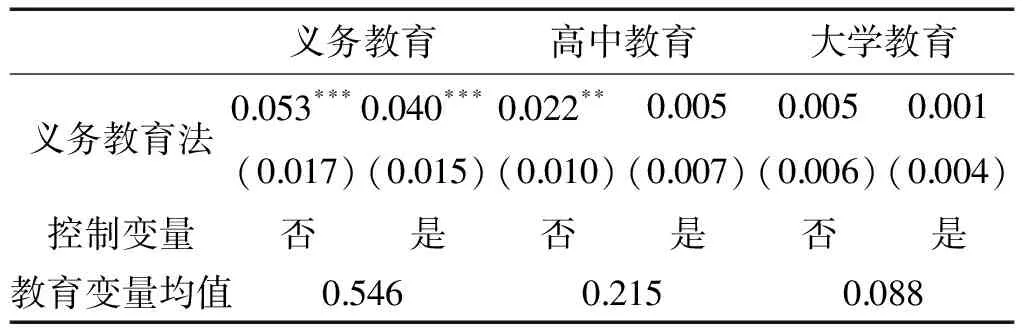
表2义务教育法对受教育水平的影响

(二)教育对健康的平均影响

第二阶段研究教育对健康的影响，构建如下结构式模型：

(2)

将式(1)代入式(2)，得到如下简化式模型：

(3)

上述模型中，healthi为个体i的健康水平；educ9i为个体i是否完成了义务教育；g(·)与j(·)均为二阶多项式；其他变量设置均与式(1)一致；μi与vi为随机扰动项。

表3是第二阶段的回归结果，估计了教育对健康的平均影响。从结构式模型的估计结果来看，教育能够在较大程度上显著改善个体的认知功能，教育对识字方面和数学方面认知功能的影响分别为1.464和1.478，且均在1%的水平上显著，在加入控制变量后，教育对这两者的影响分别为1.381和1.244，且均在5%的水平上显著。然而，教育对代表身体健康的BMI和医疗费用这两个指标的影响并不显著。

为了更好地理解教育对健康影响的效应大小，进一步地，从分位数的角度解释以标准差衡量的平均处理效应。假定正态分布，从标准化的无条件分布的中位数开始(Φ(0)=50%)(4)以正态分布作为参考，对以标准差衡量的系数估计值进行解释。，在其他条件不变的情况下，如果教育使个体的认知功能提高1.478个标准差，则该个体将处于认知功能分布的93.1%分位点处(Φ(0+1.48)≈93.1%)；如果提高1.244个标准差，则该个体将处于认知功能分布的89.3%分位点处(Φ(0+1.24)≈89.3%)。

由此来看，教育对认知功能健康的影响比较大。

简化式模型的估计结果与结构式模型相似，义务教育法的实施对认知功能健康的影响较大，但对身体健康的影响较小，尤其是医疗费用指标的系数估计值不显著。所有模型在加入控制变量后，除了医疗费用指标的系数估计值略微上升外，其他健康指标的系数估计值均有所下降，且BMI的系数估计值不再显著。

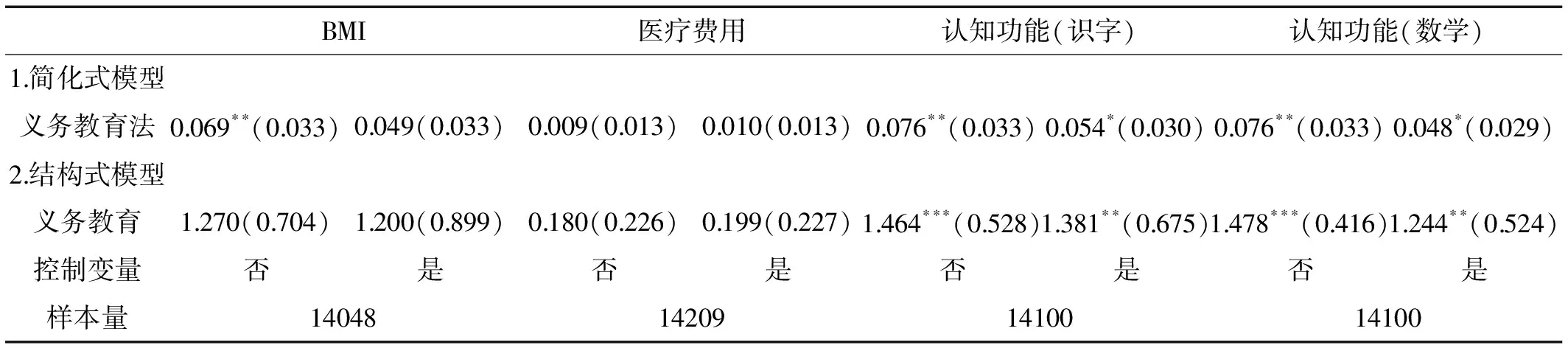
表3教育对健康的平均处理效应

除了参数估计，本文还进行了非参数估计以检验以上估计结果的稳健性。常用的非参数估计方法包括核回归和局部线性回归。在FRDD中，与核回归相比，局部线性回归的偏差更小、更有效率。[23]因此，本研究使用了局部线性回归方法，并为结果变量与处理变量设定相同的核函数和带宽。回归结果与2SLS的估计结果基本一致，教育对认知能力的影响显著，但对身体健康指标没有显著影响。

总而言之，教育对健康的平均影响的估计结果不甚理想。虽然以上研究表明，教育有助于改善认知功能健康，与程令国等(2014)[2]的研究结论一致，但无法得到教育显著改善身体健康水平的证据，且对医疗费用指标的估计结果与经验认识不符。原因可能在于，利用RDD研究教育对健康的平均影响，而忽视教育对不同分布位置的人群的异质性影响，可能会导致研究结论出现偏差。本研究将继续基于RDD框架，进一步研究教育对健康的分布处理效应，以获得更多关于教育对健康因果效应的信息。

(三)RDD有效性检验

RDD的有效性依赖于两个假设：局部平滑假设和分布函数条件连续假设，即如果不存在政策干预，潜在结果变量的期望在临界点处是驱动变量的连续函数。对应于本文研究，在满足以上假设的情况下，健康变量的期望值在出生日期临界点处的“跳跃”是由教育变量唯一引起的，衡量了教育对健康的平均处理效应。研究中往往无法直接检验这两个假设，本文从以下两个方面进行检验：一是驱动变量本身是连续的，不存在明显断点；二是影响结果变量的其他变量在临界点处是连续的，不存在明显断点。检验结果表明，本文研究设计和估计结果是有效的(5)限于篇幅，此处不再展示RDD有效性检验的结果。。

四、教育对健康的分布处理效应

(一)估计方法与模型

仅研究平均处理效应可能会掩盖教育对健康分布特定位置的不同影响，如果教育对健康的影响集中在健康分布的特定部分，那么，分布检验优于均值检验。因此，本文重点探究教育对健康的分布处理效应(DTE)。

基于RDD框架研究DTE，能够有效解决内生性问题，并分析异质性影响。[25]与传统RDD方法类似，DTE借助健康的累积分布函数(CDF)在临界点处的不连续，估计教育对健康分布的影响，其假设条件为：若不存在政策干预，潜在结果变量的分布在驱动变量上连续。本文通过检验驱动变量分布的连续性、其他变量的分布在临界点处连续，验证了分布检验的假设条件成立。

对政策干预前和干预后的累积分布函数进行设定。分别定义pre-CDF与post-CDF为从出生日期左侧(date<0)与右侧(date>0)逼近临界点的遵从者(compliers)的CDF：

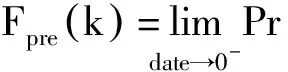
(4)

(5)

那么，通过CDF在临界点处(date=0)的断点可估计得到DTE，即给定k的值，Fpost(k)与Fpre(k)之差，用μ(k)表示：

μ(k)=Fpost(k)-Fpre(k)

(6)

对健康分布的支撑域进行离散化处理，针对每个栅格内的k点，基于式(7)估计μ(k)：

(7)

其中，1(healthi≤k)表明，如果healthi≤k，那么1(·)取值为1，否则取值为0；l(datei;k)是随k变化的关于date的二阶多项式；其他变量设置与前文一致。仍以CSLi为工具变量，使用2SLS估计式(7)，θ1(k)表示Pr(health≤k)在date=0处的差值，即μ(k)。

利用上述模型进行统计推断时，Shen和Zhang(2016)使用了基于Kolmogorov-Smirnov检验的分布检验方法，检验pre-CDF与post-CDF的差异，[25]根据其假定，基于以下简化式模型研究教育是否影响了健康分布：

1(healthi≤k)=λ0(k)+λ1(k)CSLi+l(datei;k)+X′iλ2(k)+ηi(k)

(8)

本文将使用Goldman和Kaplan(2018)提出的更加有效的多重检验方法进行分布检验。[26]第一阶段是针对整体的拟合优度检验，类似于一个两样本Kolmogorov-Smirnov检验，原假设为两个累积分布函数相同，即H0:Fpost=Fpre；第二阶段是对每一个点k进行检验，每一个原假设都为H0:Fpost(k)=Fpre(k)。检验结果能够准确给出在特定显著性水平上拒绝原假设的k的取值范围，即教育对健康存在显著影响的分布区域。

(二)估计结果及分析

与RDD的估计结果有所不同，分布检验的结果显示，教育能够显著改善身体健康和认知功能健康水平，尤其对健康分布特定位置的群体的影响非常显著。

表4为分布检验第一阶段的结果，即对累积分布函数Fpost(·)与Fpre(·)的差异进行整体检验。结果显示，BMI、医疗费用和认知功能(包括识字和数学)指标的Fpost(·)与Fpre(·)均存在差异，且均在1%的水平上统计显著，这表明教育对身体健康和认知功能健康的累积分布函数均存在显著影响。

表4分布检验第一阶段的结果

图2至图5为分布检验第二阶段在10%显著性水平上的结果(6)为避免赘述，同时限于篇幅，本文主要对10%显著性水平上的结果进行分析，1%显著性水平上的结果可向作者索要。，即教育对BMI、医疗费用(medical)、识字水平(word)和数学水平(math)的分布处理效应。可以看到，对于分布在特定位置的人群而言，教育对其BMI和认知功能均有显著的正向影响，对其医疗费用存在显著的负向影响。

从反映营养状况的身体健康指标BMI来看(图2)，Fpost(k)相对于Fpre(k)向右移动，且两者的差异随着BMI取值不同而变化，表明教育能够使BMI增加，并且对不同分布位置人群的作用大小不同。具体地，在BMI取值区间上，除了[-1.06，-0.82](分布在15%～21%分位点(7)将BMI的取值从小到大排序，如果个体位于15%分位点，则表示该个体的BMI值高于15%的人，结合样本分布和BMI取值大小，该个体的营养状况较差。的人群)外，Fpost(k)与Fpre(k)基本在[-2.13，0.36]上(分布在1.3%～72%分位点的人群)均存在显著差异，整个拒绝域涵盖了约34%的分布区间，以及65%左右的样本。换言之，当偏离BMI均值-2.13～0.36个标准差时，即当个体的体型和营养状况处于较差或正常水平时，接受教育会显著改善其身体健康水平，而样本中共有约65%的营养状况较差或正常的人，会受到教育的显著影响。进一步地，从分布处理效应的大小来看，对于分布在拒绝域内的群体，当BMI分别取极小值-2.13、0和极大值0.36时，教育能够使其BMI分别提高约0.43、0.2和0.16个标准差，相对于其自身分布位置，教育对这些群体的影响比较大(8)从分位数的角度解释，以正态分布为例，假定从标准化的无条件分布的中位数开始〔Φ(0)=0.5〕，接受教育将使得该个体从BMI分布的50%分位点处提高至58%分位点处〔Φ(0+0.2)≈0.579〕。。

因此，教育非常有助于改善体重较轻、轻度营养不良人群的身体健康水平，这一改善主要体现在体型变化上。与平均处理效应(ATE)不显著相比，分布处理效应(DTE)揭示了教育对特定群体的BMI的显著影响。

从反映疾病状况的身体健康指标medical来看(图3)，尽管两个累积分布函数整体逼近，但仍可以观察到Fpost(k)相对于Fpre(k)向左移动，且教育能够使特定分布位置群体的医疗费用减小。具体地，Fpost(k)与Fpre(k)的差异在[-0.13，0.45]上统计显著，该区域涵盖了5%的分布区间，以及10%左右的样本。换言之，当偏离均值-0.13～0.45个标准差时，即当个体的身体健康状况处于正常(医疗费用在均值附近)或较差水平(医疗费用明显高于均值)时，接受教育会显著改善其身体健康水平，这一群体在样本中占10%左右。未标准化的医疗费用均值在1075.94元左右，表明受到教育影响的多为轻症患者(如慢性病)。还可以发现，只有10%的样本分布在medical的高分位，出现这种现象的原因主要是，只有少数群体因重大疾病产生了远高于正常水平的医疗费用。进一步地，当medical分别取-0.13、0与0.45时，教育使得medical分别降低约0.02、0.06与0.2个标准差，相对于其自身分布位置，该影响仍不容忽视。

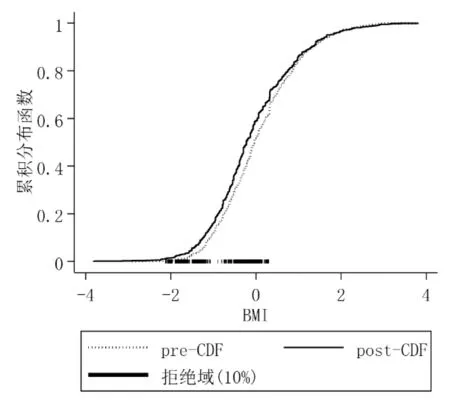
图2 教育对BMI的分布处理效应

因此，教育能够显著改善身体状况良好或有一般疾病人群的身体健康水平，这一改善主要体现在轻症预防上。可能的原因在于，受教育水平更高的人更注重且有能力(比如获得更多有效信息)预防疾病和保持身体健康。与ATE不显著相比，DTE揭示了教育对医疗费用指标的因果效应。

图3 教育对medical的分布处理效应

从认知功能健康指标word来看(图4)，Fpost(k)相对于Fpre(k)向右移动范围较大，两者的差异非常明显且随着word取值不同而变化，表明教育能够使相当一部分群体的word大幅提升，并且对不同分布位置人群的作用大小不同。具体地，Fpost(k)与Fpre(k)的差异在[-2.2，1.53]上统计显著，该区域涵盖了约96%的分布区间，以及95%左右的样本。换言之，当偏离word均值-2.2～1.53个标准差时，即当个体的识字水平较差、一般甚至较好时，教育均能显著改善其识字水平，整个样本中有95%左右的群体会受到教育的影响。进一步地，随着识字水平的逐步提高，教育对分布在拒绝域内群体的影响逐渐减小。当word分别取-2.2、0与1.53时，教育使得word分别增加约1.54、0.9与0.06个标准差，相对于其自身分布位置，教育对拒绝域内群体的影响均非常大(9)从分位数的角度解释，假定在正态分布的情况下，对于word取值分别为-2.2、0与1.53的人群，接受教育将使其分别从word分布的1.4%分位点处〔Φ(-2.2)≈0.014〕提高至25.5%分位点处〔Φ(-2.2+1.54)≈0.255〕、从50%分位点处〔Φ(0)=0.5〕提高至81.6%分位点处〔Φ(0+0.9)≈0.816〕、从93.7%分位点处〔Φ(1.53)=0.937〕提高至94.4%分位点处〔Φ(1.53+0.06)≈0.944〕。。

因此，除了样本中5%的识字水平极差或极强的人群，对于识字水平一般、较差或较好的人群而言，教育均能显著提高其识字水平，并且教育对识字水平的影响随识字水平的提高而逐渐减小。

图4 教育对word的分布处理效应

最后，从认知功能指标math来看(图5)，与识字水平的估计结果相似，教育能够使相当一部分人群的数学水平大幅提升，且对不同分布位置人群的作用大小不同。具体地，Fpost(k)与Fpre(k)的差异在[-1.95，2.13]上统计显著，涵盖了约92%的分布区间共95%左右的样本。换言之，当个体的数学水平较差、一般和较好时，教育均能显著改善其数学水平。进一步地，仍可以发现，教育对分布在拒绝域内群体的影响随着数学水平的提高，整体上呈递减趋势。当math的取值分别为-1.95、0与2.13时，教育使得math分别增加约1.99、1.32与0.06个标准差，相对于其自身分布位置，教育对拒绝域内群体的影响均非常大。

因此，除了样本中5%的数学水平极差或极强的人群，对于数学水平一般、较差或较好的人群，教育均能显著提高其数学水平，并且教育对数学水平的影响随数学水平的提高而逐渐减小。与ATE相比，DTE揭示了教育对认知功能的异质性作用以及作用规律。

图5 教育对math的分布处理效应

总体而言，与ATE相比，DTE揭示了教育对身体健康和认知功能健康的异质性影响和影响对象。从BMI和医疗费用的角度，教育能够显著改善部分(约65%)身体健康状况较差或良好的人群的身体健康；从识字水平和数学水平的角度，教育能够显著改善绝大部分(约95%)认知功能较差、一般或较好的人群的认知功能健康，并且随着健康状况的改善，教育的作用逐渐减小。

五、稳健性检验

(一)精炼样本

在一个较长时间的年龄分布中，对照组人群的健康水平可能由于时间趋势而差于处理组人群，为了控制这种影响，本文将样本精炼至义务教育法生效时年龄为13～16岁的人群，包含两年的处理组(13岁和14岁)和两年的控制组(15岁和16岁)样本，利用分布检验方法研究教育与精炼之后样本的健康的因果关系。分布检验第一阶段的结果表明教育对健康各指标的影响均在1%的水平上统计显著。第二阶段的结果与全样本估计的结果相一致，对于健康状况较差的人群而言，教育能显著改善其健康水平，包括改善体型与营养状况、降低医疗费用以及提高认知功能，一定程度上表明本文研究结果是稳健的(10)限于篇幅，精炼样本的稳健性检验结果不再赘述。。

(二)安慰剂检验

进一步地，基于两个反事实假定，分别进行两组安慰剂检验(placebo)。首先，假定义务教育法生效时间在实际生效时间之后的两年，比如1986年生效的义务教育法，在该假定中为1988年生效。为了更好地控制其他影响因素，将样本精炼为“假定的临界点”前、后各两年内。此时，处理组为义务教育法实际生效时15～16岁的群体，对照组为义务教育法实际生效时17～18岁的群体。其次，假定义务教育法生效时间在实际生效时间之前的两年，比如1986年生效的义务教育法，在该假定中为1984年生效。同样地，将样本精炼为“假定的临界点”前、后各两年内。此时，处理组为义务教育法实际生效时11～12岁的群体，对照组为义务教育法实际生效时13～14岁的群体。

对以上两组样本的分布检验的结果均显示，教育对BMI、医疗费用和认知功能均没有显著影响。图6以第二组样本为例展示了安慰剂检验的结果(10%的显著性水平)，可以看到，所有健康指标的两个累积分布函数Fpost(k)和Fpre(k)都基本重合，在任何分位点上都不存在显著差异。因此，假定的两组样本均无法得到与前文一致的结论。安慰剂检验的结果表明，本文研究结果是稳健的，教育能够显著提高特定人群的健康水平，且对处于健康分布不同位置的人群的影响大小不同。

图6 安慰剂检验

六、结论与讨论

本文首先基于RDD框架估计了教育对健康的平均处理效应(ATE)，发现教育能够在较大程度上显著改善个体的认知功能，但对代表身体健康的BMI和医疗费用这两个指标并无显著影响。

考虑到教育可能对不同分布位置人群存在异质性影响，本文仍基于RDD框架，进一步使用分布检验方法估计了教育对健康的分布处理效应(DTE)。研究主要发现：第一，不管是身体健康还是认知功能健康，教育均能显著改善健康状况良好或较差的人群的健康水平，还能在一定程度上改善认知水平较好的人群的认知功能健康，且教育对认知功能健康的影响大于身体健康；第二，整体来看，随着健康状况的改善，教育对健康的影响呈递减趋势，健康状况较差的人受到的影响较大。

具体到衡量健康水平的各个指标：对于样本中约65%的体型与营养状况良好或较差的人而言，教育使其BMI显著提高0.16～0.43个标准差左右；对于样本中约8%的身体状况良好或患有一般疾病的人而言，教育使其医疗费用显著降低0.02～0.2个标准差左右；对于样本中约95%的识字水平较好、正常或较差的人而言，教育使其识字水平显著提高0.06～1.54个标准差左右；对于样本中约95%的数学水平较好、正常或较差的人而言，教育使其数学水平显著提高0.06～1.99个标准差左右。可以看到，教育对认知功能健康的作用和影响范围均大于身体健康。另外，从分位数的角度理解标准差，教育对这些健康指标的影响均比较大。

本研究的政策启示主要在于：一是充分利用教育来提高人口的身体健康和认知功能健康水平，以教育强化健康人力资本，应对老龄化挑战；二是教育对亚健康状况的人群具有更大的影响，因此，在改善农村贫困地区人口的教育与健康方面，合理地增加教育投入可能会达到事半功倍的效果，从而为农村减贫做出一定贡献。