基于旅客出行选择特征的高速铁路浮动定价策略研究
陈方遒,景 云,2,郭思冶
(1.北京交通大学 交通运输学院, 北京 100044;2.北京交通大学 智慧高铁系统前沿科学中心, 北京 100044)
高速铁路(以下简称“高铁”)是国家现代化高质量综合立体交通网的重要一环,能够有效减少城市间的出行时间,带动城市经济发展。高铁票价是影响出行需求的主要因素,采用浮动定价策略,可以有效协调席位资源配置,合理引导旅客需求,提高铁路企业客票收益。京沪高铁于2020年12月23日起实行浮动票价试点,将票价分为9个等级,预售期开始时公布价格,预售期内保持价格不变。
目前京沪高铁浮动定价主要考虑列车的旅行时间、发车日期是否为周五或者周日两个因素,未考虑出发和到达时刻等。本文通过分析旅客出行选择特征,改进现有的分级浮动定价策略,依据客座率设计浮动定价方案,从而均衡客流时空分布,提高企业客票收益。
分析旅客出行选择行为可以为动态定价提供依据。Talluri等[1]构建Logit模型研究影响铁路旅客出行选择行为的因素,提出铁路客票动态定价策略。单杏花[2]通过分析铁路旅客选择行为,提出静态定价策略和动态定价策略相结合的铁路客票收益管理体系。秦进等[3]在分析旅客出行价格需求弹性的基础上,构建基于Logit模型的客流弹性函数,建立以期望客票总收入最大化为目标的多列车多时段的动态定价与票额分配协同优化模型,有效提高铁路运输企业的客票总收益水平。
精确预知客流规律可以为铁路部门实施动态定价策略提供关键参考。建立客流预测模型是短期客流预测领域最主要的应用方法,Tsai 等[4-5]设计了两种动态神经网络模型,在短期客流预测结果均取得了低于20%的平均绝对百分误差。王芳杰等[6]通过LightGBM模型预测公交的行程时间,结果表明该模型关键指标均大幅度优于参照组。杨文淇[7]建立基于LSTM神经网络的城轨新线开行下常规公交客流预测模,预测城轨新线开通后的客流量变化情况。单一客流预测模型性能有限,为进一步提升预测能力,融合客流预测模型得到发展。Davis等[8]利用K-NN和Linear Time-series结合的融合模型对高速公路交通量进行短时预测;Jing等[9]建立LGB-LSTM-DRS的局部最优融合预测模型对城市轨道交通对外客运枢纽进行客流短时预测。
差别定价是一种重要的动态定价策略,可有效发挥价格杠杆作用。目前国内针对高铁差别定价问题的研究主要面向同一OD多趟列车展开。张秀敏等[10]通过对同一席位的不同旅客进行市场细分,研究不同情况下的旅客列车席位最优定价问题。卜伟等[11]针对同一线路同一距离的高铁列车应依据出行时刻、出行人群等维度在票价形成过程中发挥的作用效果,提出普遍实施差别定价,尝试多维度折扣。李博[12]在列车运行图固定的条件下,构建离散时间的动态规划联合定价模型和同一OD非平行车次间的差别定价模型,研究高铁动态定价问题。
综上所述,目前铁路客票定价策略研究在旅客出行选择行为方面,主要通过构造敏感函数,研究用动态定价策略后旅客的选择行为。在客流预测方面,对道路及城市轨道交通的研究较多,对较强随机性、非线性及突变性下的高速铁路客流研究不够精细;在差别定价方面,主要依靠传统经验公式、列车单一属性等因素对列车进行分级,较少研究多影响因素的差别定价策略。
本文提出可处理非时序特征的改进的LSTM模型,对不同价格水平下即将开售车次的余票进行精准预测;利用GBDT算法对乘客的特征变量进行提取,解决了车次余票相同时定价分级问题,针对现行的定价策略提出改进方案。
1 高铁客票分级定价模型
高铁客票定价分级就是通过提取高铁服务特征,预测市场需求,确定实际发车日不同高铁车次的票价等级。本模型通过预测发车日各次列车的上座率,确定票价等级,使得余票紧张的车次价格等级较高。
1.1 模型假设
(1)基础票价等级为553元。
(2)为方便比较,设定列车运行图、票价等级与各等级数量与现行方案一致。
(3)仅考虑二等座的定价策略。
1.2 浮动定价规划模型
铁路企业客票总收入S为
(1)
式中:ek为第k列车的二等座上座人数,可通过发车日需求预测模型对余票数进行推算;pk为第k列车的二等座的票价,元。
浮动定价模型为
(2)
s.t.
P=(P1,P2,P3,…,Pj)T
(3)
Ojk=(o1k,o2k,…,ojk)
(4)
o1k+…+ojk=1
(5)
(6)
(7)
式中:P为二等座票价划分成j个定价等级的票价列向量;Ojk为定价等级j的第k列车编码向量;ojk为定价等级j的第k列车独热码“one-hot”编码值,取值0或1;mj为定价等级j的车次数量;jbase为基础票价对应的定价等级。
求解该模型,可得到预计票务收入最大化时各列车的定价等级分配模式。
2 发车日需求预测
2.1 模型构建
Xk=(x1,x2,…,xt,…,xn)为车次k在票价制定日前n天随时间变化的时序性特征。利用LSTM层对Xk进行处理,该层中任意t时刻单个LSTM单元的输出值ht,取决于该时刻输入门取值ct与输出门取值ot。ht为
ht=ot×tanh(ct)
(7)
ct取决于遗忘门的取值ft。ft、ct和ot分别为
ft=σ(Wf[ht-1,xt]+bf)
(8)
(9)
ot=σ(Wo[ht-1,xt]+bo)
(10)
it=σ(Wi[ht-1,xt]+bi)
(11)
(12)


(13)
式中:Lk为LSTM层输出;Wd1为第一个Dense层的权重矩阵;Wd2为第二个Dense层的权重矩阵;bd1为第一个Dense层的偏置项;bd2为第二个Dense层的偏置项。
为衡量模型预测准确性,基于均方误差RMSE,改进的LSTM模型预测误差E为
(14)
式中:yk为发车日实际余票数;K为总发车次数。
综上,改进的LSTM模型通过顺序连接两个Dense层,在第一个Dense层中输入非时序特征,弥补了传统LSTM模型只能处理序列数据的不足。
2.2 模型求解
发车日需求预测模型涉及全连接单元与LSTM单元两种单元。基于反向传播算法,利用每个单元的权重矩阵与偏差计算该单元输出值的梯度,通过链式求导,求得所有单元对最终模型输出值的梯度。沿梯度方向迭代权重矩阵与偏差,使模型收敛。随机梯度下降法步骤如下:
Step1设定最大迭代次数nepochs与学习率α。
Step2随机抽取某一车次k的特征数据[Xk,Jk]。
Step3计算式(1)~式(7)中所有权重矩阵与偏置项的梯度方向。
Step4沿梯度方向对式(1)~式(7)中所有权重矩阵与偏置项进行迭代更新,即Wnew=Wold+α×dW;bnew=bold+α×db。
Step5若达到最大迭代次数,算法终止;否则,返回Step2。
对式(13)直接求导可得其权重矩阵与偏差对应的梯度值,但由于LSTM单元前向传播具有两个方向,且需考虑其门结构特征,因此需使用以下方法对其权重矩阵与偏差求取对应梯度值。

(15)
(16)
(17)
(18)
式中:
(19)
Ft=dct×ct-1+ot×[1-tanh2(ct)]×ct-1×dht
(20)
Ct=dct×it+ot×[1-tanh2(ct)]×ot×dht
(21)
对于各权重矩阵,则有
(22)
(23)
(24)
(25)
对于各偏置项,有
(26)
(27)
(28)
(29)
综上,迭代方向为所有LSTM单元内权重矩阵与偏置项的梯度方向。
3 发车日非时序特征提取
由于目前铁路部门实施“一日一图”开行模式,存在列车时序性特征Xk不完整或非时序特征Ik不统一的情况,仅使用发车日需求预测模型会出现无法完整预测所有列车需求的情况。此外,当历史余票全部为0或因其他因素导致模型输出余票相同时,仍需要按余票以外的特征进行进一步的等级划分,确定定价优先级。
GBDT为一种集成模型,其集成对象为二分决策模型CART。运用Gini指数衡量样本不纯度,令D为父节点样本集合,则该节点的Gini指数G(D)为
(30)
Pc=|c|/|D|
式中:Pc为从父节点D进入其子节点c的概率;|·|为计数函数,保证分裂不具偏向性。D1和D2为父节点D分裂后的两个子节点对应集合,其Gini指数递进关系为
(31)
CART算法步骤如下:
Step1遍历所有特征,寻找Gini指数最小的节点D*和对应特征A*。

Step3验证是否满足停止分裂条件,满足则算法终止;否则,转到Step1。
设GBDT内由m个CART集成,令CART的输出分别为T1(Ik),T2(Ik),…,Tm(Ik),则GBDT的输出gm为
(32)
去掉最后一个CART,GBDT的输出gm-1(Ik)为
(33)
考虑GBDT可加性,其误差可泰勒展开,忽略二次以上项式,误差递归形式为
(34)
为保证误差在添加Tm后下降,即需满足
E[yk,gm(Ik)]-E[y,gm-1(Ik)]<0
(35)
(36)
将式(34)、式(35)代入式(36),则对于Tm(Ik)有
(37)
式中:Tm(Ik)为负梯度方向。
GBDT算法步骤如下:
Step1初始化CART模型T1(Ik)。

Step3使用CART模型Tm(Ik)拟合 Step2中的负梯度方向。

Step5验证是否满足终止迭代条件,满足,到转Step6;否则,转到Step2。
Step6提取T1(Ik),T2(Ik),…,Tm(Ik)在Step1中寻找到的A*划分Ik的特征空间。
综上,本文利用GBDT模型的中间节点,发挥其高可释性特点,划分高铁列车非时序特征空间。依据余票数据缺失或相同的车次的非时序特征,对余票数据缺失车次利用相似车次进行数值估计,对余票数据相同车次确定优先级。
4 票价等级分配流程
针对历史数据缺失导致无法直接计算出ei和过多车次余票相同导致票价最优解不唯一的情况,本文设计基于逐次逼近法的票价等级分配流程,步骤如下:
Step1利用发车日需求预测模型,预测各数据完整车次的余票估计值。
Step2依据Step1得到的估计值,利用发车日非时序特征提取模型,构建决策树。
Step3若当日存在数据不完整车次,利用Step2中决策树找到最终节点,利用该节点其他车次余票的平均值估计余票。
Step4基于余票数量从少到多排序,按照价格等级从高到低依次分配,该等级数量分配完毕后进入下一等级,分配至基础票价等级时停止分配。
Step5基于余票数量从多到少排序,按照价格等级从低到高依次分配,该等级数量分配完毕后进入下一等级,分配至基础票价等级时停止分配。
Step6余下所有车次分配基础票价等级。
以上步骤中,若当日存在余票数相同过多,高定价等级容量不足的情况,需计算各车次优先级∑K(A)×10Ad。K(A)为Step2中提取的非时序特征A的判定函数,若存在特征A则取其值为1,反之为-1;Ad为特征A在决策树中的层数,优先级高的车次分配到更高的票价等级。
5 算例分析
基于目前京沪高铁运营情况,参照现行票价分级方式,明确票价等级划分标准,将票价分为9个等级,见表1;参照京沪高铁购票流程,选取1个时序特征与4个非时序特征作为模型输入,见表2。

表1 京沪高铁现行定价等级划分标准

表2 模型特征选择标准
基于表2中特征对现行票价进行相关性分析,结果见图1。图1中,横纵坐标为特征变量,第i行第j列的方块颜色深浅表示横坐标上第i个特征与纵坐标上第j个特征的相关程度,颜色对应的值如右侧色条所示,为相关系数,记为
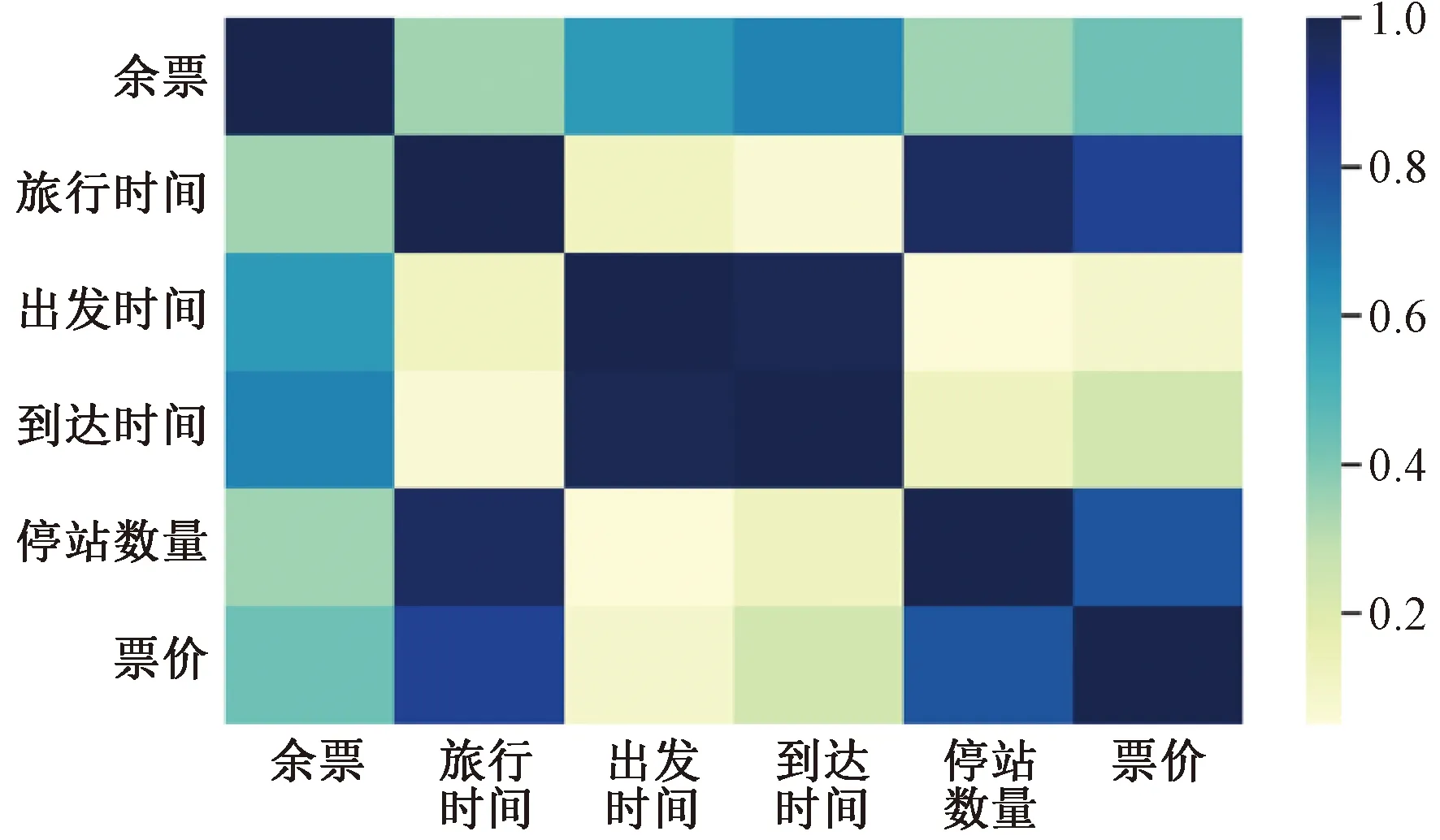
图1 特征-票价相关性热力图
(32)
式中:X与Y为需要计算的两个特征变量;cov(X,Y)为X与Y的协方差;var(X)与var(Y)分别为X与Y的方差。
由图1可知,票价与旅行时间和停站数量相关,现行的票价制定策略仅考虑了列车速度相关的因素,缺少对余票、出发时间和到达时间的考虑。
基于2019年11月京沪高铁余票数据,提取表2中的特征进行标准化后,按时间先后顺序排序,将前70%数据作为训练集,后30%数据作为测试集,预测发车日需求。
为保证模型复杂度一致,设定所使用的模型均仅由输入层、循环层和输出层组成,循环层单元数均设置为32,学习率α均为0.001,模型对比结果见图2。

图2 模型对比结果
从训练集效果来看,高铁旅客需求预测对非时序特征变量较为敏感,考虑非时序特征的改进的LSTM模型比3种常用的深度学习模型误差更小、鲁棒性更强。
从测试集效果来看,RNN模型的均方误差随迭代次数始终上下波动,稳健性较差;普通的LSTM与GRU稳健性相似,强于RNN但弱于改进的LSTM;改进的LSTM的均方误差在迭代中稳定下降,其稳健性显著高于其他模型。80轮迭代后4种模型的最终误差见表3。

表3 4种模型最终误差
由表3可知,改进的LSTM在训练集中相较于其他三类模型提升幅度约为30%,在测试集中提升幅度约为10%,表明改进的LSTM具有更强的适应能力,且无过拟合现象。
利用GBDT模型提取到的列车特征见图3,将第4节中计算所得的车次优先级标定在弧上。对由于数据缺失无法预测余票情况的车次,按同节点中余票情况的平均值四舍五入取整估计。

图3 模型提取特征二分树
以11月25日的定价体系为例,基于浮动定价模型,求得结果见表4。由发车日需求预测结果可得,当日预计有8次列车余票均为0。因G123为数据缺失车次,无法对余票直接进行预测,通过节点平均,估计当日余票也为0。因此预计当日共9次列车余票为0,超过了最高定价等级的数量设定,需确定优先级。基于图3所提取的特征进行排序,得到的预计余票及其定价等级排序情况见表4。

表4 11月25日定价等级分配结果
基于表2特征对表4所得新票价体系进行相关性分析,其中余票使用真实数据而非预计余票,去除与旅行时间高度重合的停站数量特征,按图1方式进行相关性分析,结果见图4。

图4 特征-新票价相关性热力图
可见,新票价体系可有效反应余票紧张程度,并充分考虑了列车出发与到达时间。从收益管理角度来看,与原票价体系相比,新票价体系下铁路部门收入提升了24 390元,能够更好满足运输市场需求。
6 结论
本文针对列车余票与非时序特征相关性大的特点,基于改进的LSTM模型,对发车日当天余票情况实现精准预测;针对铁路热门车次多但该等级车次数量有限的特点,基于GBDT模型提取列车特征,分配车次优先级,同时解决部分车次数据缺失问题;构建以铁路企业收益最大为目标的定价模型,并采用逐次逼近算法求解,提出基于现行浮动定价策略提出改进方案。
算例结果表明,改进LSTM模型与三种常用深度学习时间序列预测模型相比,需求预测的标准化均方误差更低;定价模型有效为各列车分配了合理的定价等级,且与现行浮动定价策略相比,所提出改进的浮动定价策略可提高铁路部门单日收益24 390元。为便于比较,本文在票价分级方式上采用现行票价分级方案。在后续研究中,将进一步完善考虑多特征融合下的高铁票价分级方法,构建能够动态适应客运市场变化、协调席位资源配置关系、引导客流需求的浮动定价理论体系。

