关于无人机集群对地目标跟踪技术的研究

韩 斌， 赵亚飞

(中国电子科学研究院，北京 100041)

0 引 言

随着无人机集群技术的快速发展，对地面动目标的跟踪和识别成为无人机集群应用的热点问题[1-3]。无人机集群在执行地面目标跟踪时，通过其携带的可见光相机和雷达等传感器，能够获取目标的位置和速度等状态信息[4]，但是测量噪声的存在导致直接使用这些位置信息时无法获取相对精确的状态信息，无法实现精确跟踪和导引打击。此外，当目标受到短时障碍物遮挡导致无法获取目标状态信息时，需要基于先验信息实现对目标状态的预测和估计[5-6]。

针对无人机集群对地目标跟踪问题，文献[7]提出了一种基于最小二乘拟合的运动目标测速方法，实现了无人机对运动目标速度的测量，精度较高。文献[8]提出了一种针对小目标的目标跟踪算法，通过基于分类学习的协同训练算法实现目标跟踪，提高分类器的判别能力，但在复杂环境下，无人机集群协同跟踪地面目标过程中，存在算法复杂、需要训练或先验知识等问题，在应用时需要较高的硬件条件和配套训练设备，无法在无人机集群中广泛应用。

基于上述考虑，本文研究一种用于无人机集群对地目标的状态估计算法，将噪声项从测量项中滤掉，并且当目标的状态信息丢失时，滤波算法能够根据需要给出目标的预测状态信息。

1 目标状态估计方法

令Te为位置估计更新周期，假定k时刻无人机机载传感器测量的地面目标坐标x和y满足

(1)

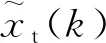
1.1 通过航向和速度估计目标位置

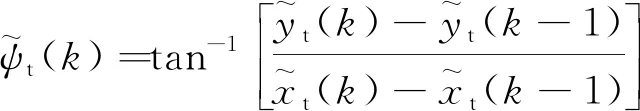
(2)

(3)

一般说来，对过去数据掌握越多，未来预测越精确，但是批量处理会大大增加计算和内存的负担[9]。为了解决这个问题，批量处理只是针对一定量的数据进行计算，比如采用序贯估计方法，只需要采用当前时刻和前一采样周期内的数据就可以实现状态估计。

测量模型(采用二阶状态估计器)可以表述为

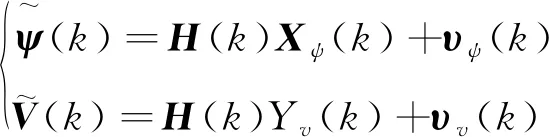
(4)

其中，

式中：运动方向和速度的计算用到了非线性方程，因此，υψ(k)和υv(k)为非零均值高斯白噪声。

在进行最小二乘估计时，至少需要知道4个位置的测量信息，其估计过程为

(1)批量估计

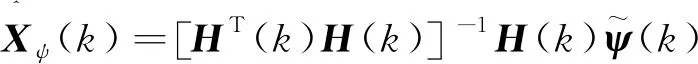
(5)

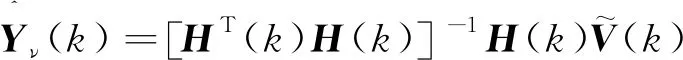
(6)

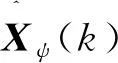
(2)序贯估计

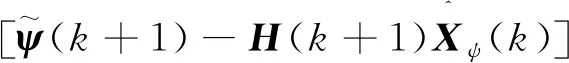
(7)

K(k+1)=P(k)HT(k+1)·

[H(k+1)P(k)HT(k+1)+W-1(k+1)]-1

(8)

P(k+1)=[I-K(k+1)H(k+1)]P(k)

(9)

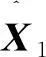
通过批量估计序贯估计过程，目标的运动方向和速度估计的计算公式为

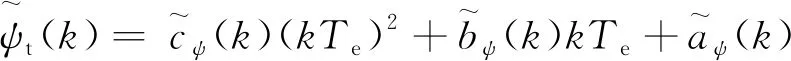
(10)

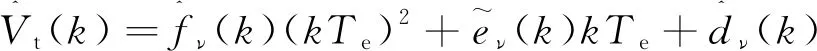
(11)

根据运动方向和速度的估计结果，可以计算目标的位置坐标

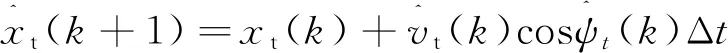
(12)

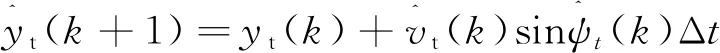
(13)

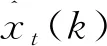
1.2 直接目标位置估计

同样地，基于二阶状态估计器测量模型表述为

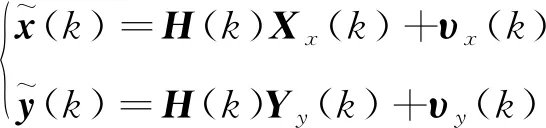
(14)

式中：υx(k),υy(k)为噪声向量，相关向量和矩阵的分量形式为

Xx(k)=[ax(k),bx(k),cx(k)]T

Yy(k)=[dy(k),ey(k),fy(k)]T

(15)

式中：n=min{nsw,km}，nsw是测量时间步长数的最大值，km为在状态估计中采用的时间步长数；ax(k),bx(k),cx(k)为对状态量x进行估计时的采样点权重系数；dx(k),ex(k),fx(k)为对状态量y进行估计时的采样点权重系数。

基于位置的最小线性二次估计至少需要三个位置测量信息才能进行运算，而采用运动方向和速度的最小线性二次估计则需要四个位置信息才能进行运算，这是因为四个位置信息需要计算出三个航向和速度量。估计方程为

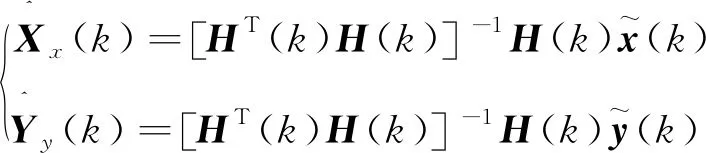
(16)

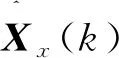
(17)

由于

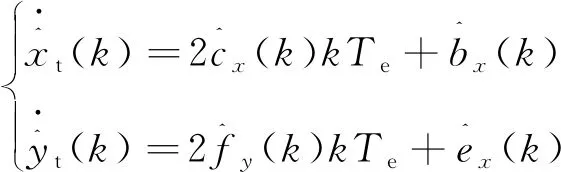
(18)

根据运动学方程，目标的速度和航向估计可以写成

(19)

1.3 两种方法的对比

上述两种方法都采用最小二乘估计方法，但是有两点存在不同。

1)第一种通过航向和速度来估计位置的方法，从批量处理模式开始，然后再转为序贯模式进行数据处理；而第二种直接位置估计方法则一直处于批量处理模式，并通过滑动窗口协议进行信息量控制，避免数据阻塞。

2)第一种估计方法采用是根据位置测量结果，计算速度和航向，然后通过最小二乘法计算得出的新的速度和航向，再通过运动学关系转化为新的位置和速度；而第二种方法通过从位置的测量结果估计下一个位置。

图1给出两种目标位置估计方法的仿真对比结果，仿真场景设定为目标连续右转，并且随着时间增加到900 s，速度逐渐增加，在第700 s时，目标的测量信息丢失。

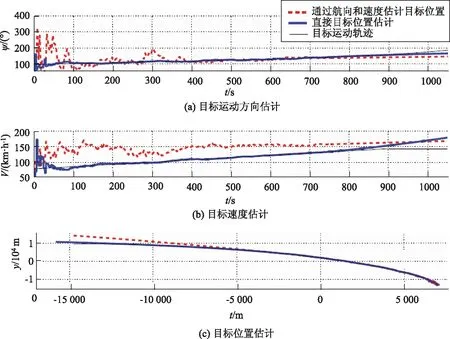
图1 两种方法的仿真对比

从仿真结果可以看出，第一种估计方法比第二种估计方法航向角收敛速度更快，第二种估计方法的速度并未收敛，当测量信息丢失时，第一种估计方法的偏移量很小。

2 无人机集群目标位置估计

在多无人机进行协同探测时，通过信息共享可实现信息融合处理，提高目标识别的精度。假定无人机集群的通信容量能够允许无人机间实现测量信息共享，并统一发送到某架无人机上进行数据融合处理。

假定无人机i可以通过敏感器测量到目标的x和y坐标

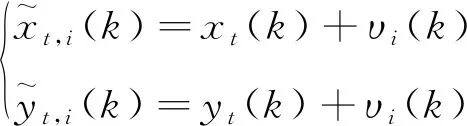
(20)

前文中提及单无人机可基于目标的测量结果，采用二阶最小二乘估计器实现对目标的位置坐标估计。

(21)

而在多无人机协同探测时，无人机在进行位置估计时，不仅要考虑自己对目标位置的感知信息，还需要考虑临近无人机对目标的感知信息。

由于目标的x和y位置坐标估计没有区别，下文我们以x位置坐标为例讨论位置估计计算。无人机i的x位置测量信息向量可以写成：

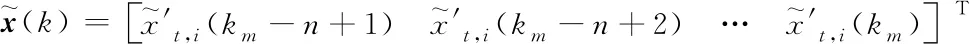
(22)

其中，

(23)

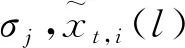
3 仿真分析

为了证明多机协同侦察带来的优势，可以通过仿真场景进行验证。假定目标初始位置为(-5 000 m, -20 000 m)，并且按照如下方程表述的轨迹运动：

(24)

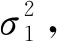
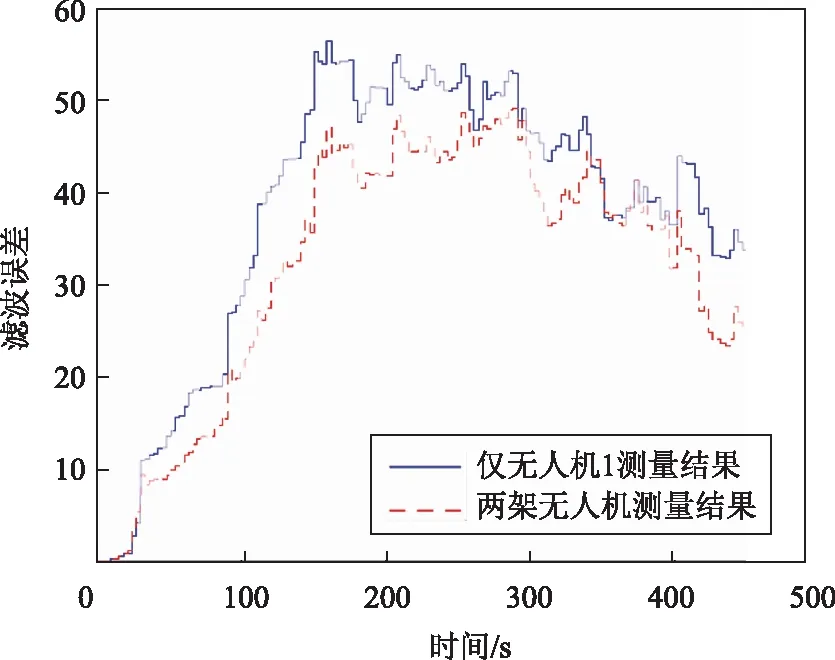
图2 无人机对目标位置的估计误差

位置估计误差定义为

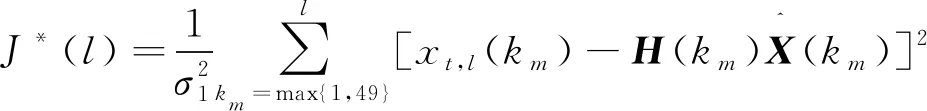
(25)

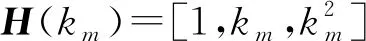
图2中给出两种情形下的误差估计，随着测量数据的不断增多，测量信息矩阵的阶数在最初的150 s内不断增加，直至达到最大值，位置误差估计也逐渐增加。在整个仿真过程中，尽管多机融合过程中误差的协方差更大，但多机融合得到的位置估计误差比单一无人机位置估计的误差要小。因此，无论在任何时候，如果能够获得多机的目标感知数据，那么采用多机融合处理得到的位置信息远比单一无人机的目标位置感知信息更加精确。

4 结 语

本文针对无人机集群对地面动目标跟踪问题进行了研究，得到了如下两点结论。

1)通过航向和速度估计目标位置与直接目标位置估计方法相比，航向角收敛速度更快，当测量信息丢失时，通过航向和速度估计目标位置估计方法的计算结果与真实值的偏移量更小。

2)无人机集群在目标信息获取和跟踪时更具优越性，仿真表明无人机集群在进行目标跟踪时跟踪误差更小，尤其是在长时间跟踪的情况下，集群的优势更加明显。