磁流体润滑螺旋槽机械密封环角变形计算

张鹏高,顾伯勤,周剑锋,魏 龙,冯 秀

(1.南京工业大学 机械与动力工程学院,江苏 南京 211800;2.南京科技职业学院 江苏省流体密封与测控工程技术研究开发中心,江苏 南京 210048)

磁流体是一种新型功能材料,它是将纳米尺度的磁性固体颗粒均匀地分散在基液中而形成的稳定胶体溶液[1]。磁流体与普通流体最大的不同之处就在于磁流体具有磁性,其磁性来源于磁流体组成中的固相磁性微粒[2],磁流体的运动可通过外磁场加以控制[2-3]。文献[4-5]根据磁流体黏度随磁场强度变化的特点,以磁流体为润滑介质,提出一种非接触式磁流体密封结构,并试验研究了其动压润滑特性,结果表明:在非接触式机械密封中,磁流体润滑膜的黏度对密封性能和泄漏率的影响至关重要[4-6]。

在运行过程中,机械密封的密封环因受力、受热不均匀而产生变形,使密封环端面产生径向锥度,形成收敛型或发散型间隙,从而引起密封环磨损和端面泄漏加剧,使机械密封使用寿命缩短[7-8]。

目前,对于机械密封环的变形研究主要是通过数值模拟的方法得到的,运用直观的解析法计算密封环端面变形的研究鲜见报道,而对于磁流体润滑的机械密封环角变形研究也尚未开展。

本文利用文献[9]的方法研究密封环端面因不均匀分布的压力而产生的角变形及角变形对磁流体膜动压润滑性能的影响。推导了外磁场作用下磁流体膜的黏度公式,基于Muijderman窄槽理论,计算了磁流体润滑螺旋槽机械密封压力场和磁流体膜的开启力,分析了操作参数和螺旋槽结构参数对磁流体膜厚度和密封环角变形的影响。

1 磁流体润滑螺旋槽机械密封机制

1.1 磁流体润滑螺旋槽机械密封结构

磁流体润滑螺旋槽机械密封主要由动环、静环和磁场发生器组成(图1)。螺旋槽是通过激光刻蚀在动环端面上的(图2)。当带有螺旋槽的动环旋转时,磁流体被泵入密封环端面间,动环、静环在磁流体膜动压效应的作用下实现端面的非接触式控制,通过控制外磁场强度来调节磁流体的黏度,从而使磁流体膜产生不同的动压,实现流体动压效应的非接触式控制,满足压力波动的要求。

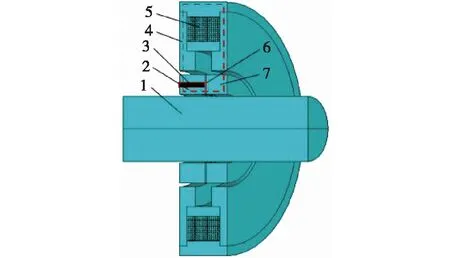
1—转轴;2—静环;3—引流孔;4—磁回路;5—磁场发生器;6—磁流体膜;7—动环图1 磁流体润滑螺旋槽机械密封 Fig.1 Spiral groove mechanical seal lubricated by magnetic fluid

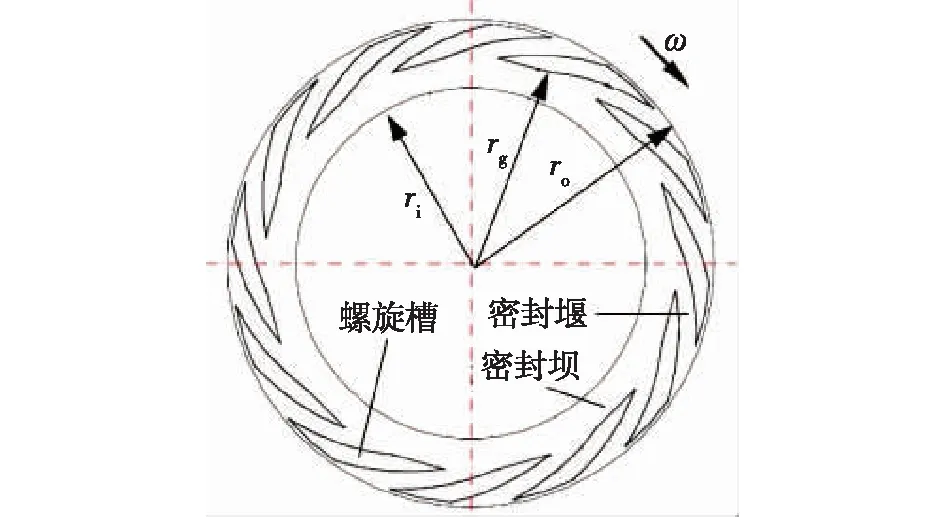
ri—密封环内径;rg—螺旋槽根径;r0—密封环外径;ω—密封环旋转角速度图2 动环端面的螺旋槽Fig.2 Spiral grooves on end face of rotating ring

1.2 密封环端面压力变形模型

对磁流体润滑螺旋槽机械密封的动压润滑特性进行研究发现:受螺旋槽的影响,磁流体在动环、静环端面间的压力，周向呈周期性、径向由内径向外径先升高后降低分布,在螺旋槽根径处的磁流体膜压力最大[10]。

由于磁流体膜压力径向的不均匀分布,使动环、静环在径向产生一定的夹角(图3)。假设螺旋槽机械密封环端面受压力变形后的轮廓曲线为直线,变形后径向磁流体膜厚度可表示为[11-12]

hi=h0+(r-ri)tanβ

(1)

式中:hi为磁流体膜厚度,m;h0为密封环内径处磁流体膜厚度,m;r为密封环半径,m;β为密封动环与静环的夹角,rad。

动环的受力平衡条件为

Fc=F0

(2)

式中:Fc为闭合力,N;F0为磁流体膜的开启力,N。

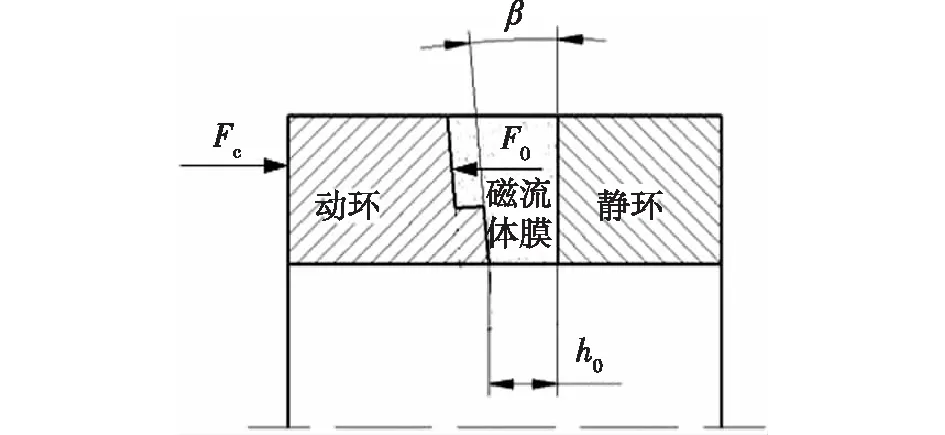
图3 密封环受力变形模型Fig.3 Model of deformation generated by pressure of sealing rings

2 外磁场中磁流体的特性参数

2.1 外磁场中磁感应强度与电流的关系

Zhou等[4]通过试验确定了外磁场中磁感应强度与电流的关系，如式(3)所示。

B=0.05(I-1)+0.05

(3)

式中:B为磁感应强度,T;I为线圈中的电流强度,A。

2.2 外磁场中磁流体黏度

外磁场中磁流体的黏度公式为[2]

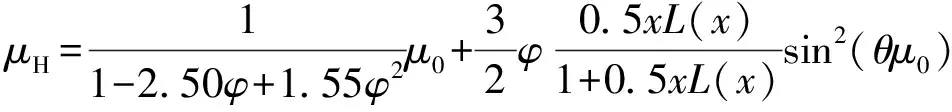
(4)

式中:μH为外磁场中磁流体的黏度,Pa·s;φ为磁流体中固体颗粒的体积分数,%;μ0为磁流体基液的黏度,Pa·s;θ为磁场强度矢量与固体粒子速度矢量的夹角,(°);L(x)为Langevin函数,x为Langevin函数变量。

由Langevin方程可得如式(5)所示的关系式[13]。

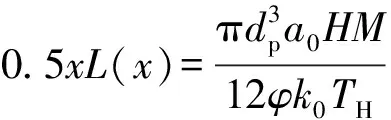
(5)

式中:dp为固体颗粒直径,m;a0为真空磁导率,a0=4π×10-7H/m;H为磁场强度,A/m;M为磁化强度,A/m;TH为磁流体温度,K;k0为玻尔兹曼常数,k0=1.38×10-23J/K。

根据电磁学知识可知,M、B和H的关系为[14]

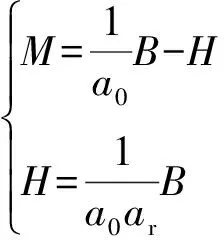
(6)

式中:ar为相对磁导率。

外磁场作用下,进入磁场的磁性粒子沿磁场方向排列成链状结构,同时发生磁矩偏转,磁性粒子与基液分子之间的摩擦加剧,使磁流体的黏度增大。当磁场方向与磁流体运动方向垂直时(θ=90°),磁流体黏度增大幅度比平行时的增大幅度大[15]。此时,更有利于实现通过控制外磁场大小以调节磁流体黏度的目的[4-5]。

当θ=90°时,将式(3)、(5)、(6)代入式(4)中,可得

(7)

2.3 磁流体密度

磁流体的密度如式(8)所示[2]。

ρH=(1-φ)ρ0+φρp

(8)

式中:ρH为磁流体的密度,kg/m3;ρ0为磁流体基液的密度,kg/m3;ρp为固体颗粒的密度,kg/m3。

3 磁流体膜特性计算方法

3.1 磁流体膜压力控制方程

令a=tanβ,b=h0-ritanβ,则磁流体膜厚度计算式(式(1))可写成

hi=ar+b

(9)

根据Muijderman窄槽理论[16-17],磁流体沿密封环径向的磁流体膜压力控制方程如式(10)和(11)所示。

密封坝区

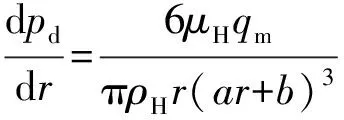
(10)

螺旋槽区

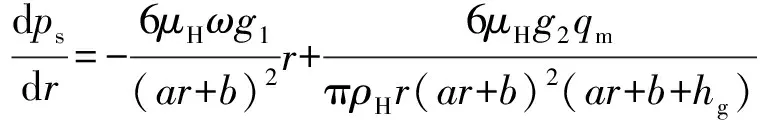
(11)

式中:pd为密封坝区的介质压力,Pa;qm为磁流体质量流量,kg/s;ps为螺旋槽区的介质压力,Pa;hg为螺旋槽深度,m;g1、g2为螺旋槽系数。

g1、g2具体表达式分别为

(12)

(13)

式中：α为螺旋角,(°);γ为密封堰宽与螺旋槽宽之比(堰槽宽比);H1为密封坝区与螺旋槽区磁流体膜厚度之比,H1=h0/(h0+hg)。

3.2 磁流体膜压力控制方程求解

式(10)和(11)满足的边界条件:在密封环内径处，p(r=ri)=pi；在密封环外径处，p(r=r0)=p0。

对式(10)积分,并代入边界条件,可得

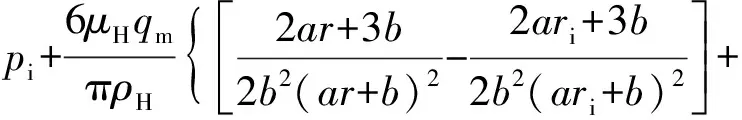
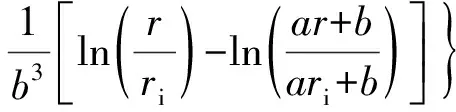
(14)

式中:pi为密封环内径处的介质压力,Pa。

将r=rg代入式(14),可得螺旋槽根径处的压力(pg)，如式(15)所示。

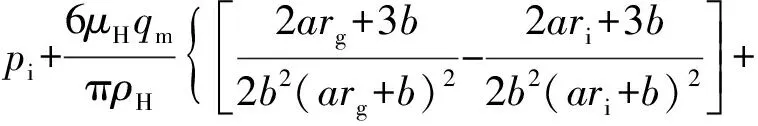
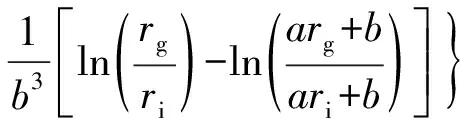
(15)

由式(15)可知

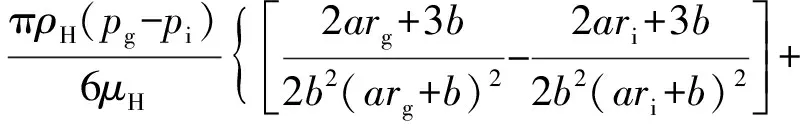
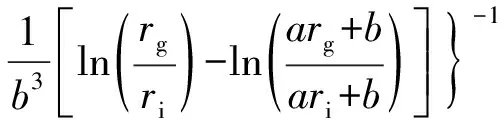
(16)

对式(11)积分,并代入边界条件,可得

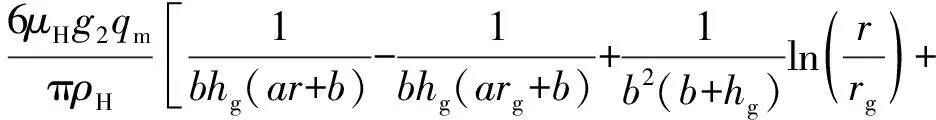
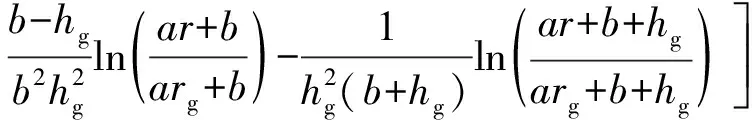
(17)

将r=r0代入式(17),可得

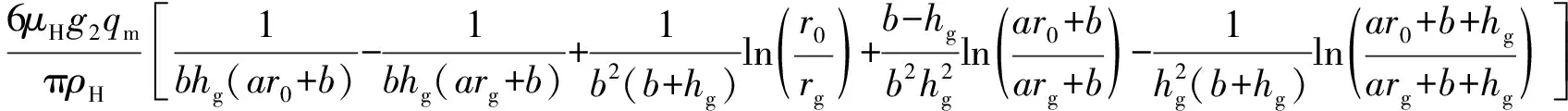
(18)

式中:p0为介质压力,Pa。

将式(16)代入式(18)中,即可确定pg。再将pg代入式(16)可确定泄漏率。

3.3 磁流体膜开启力

由图2可知:密封环端面间磁流体膜的开启力等于密封坝区(ri→rg)磁流体膜的开启力(Fd)与螺旋槽区(rg→r0)磁流体膜的开启力(Fs)之和。

密封坝区(ri→rg)磁流体膜的开启力(Fd)为

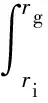
(19)

将式(14)代入式(19),并积分,可得

(20)

螺旋槽区(rg→r0)磁流体膜的开启力(Fs)为

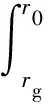
(21)

将式(17)代入式(21),并积分,可得

(22)

磁流体膜的总开启力(F0)为

F0=Fd+Fs

(23)

4 密封环端面压力变形计算流程

本文先计算动环、静环端面平行时(β=0),开启力和闭合力达到平衡时的磁流体膜厚度。在此厚度基础上,再根据轴向力平衡条件(F0=Fc),计算动环、静环间的夹角(β)。密封环端面压力变形的计算流程如图4所示。

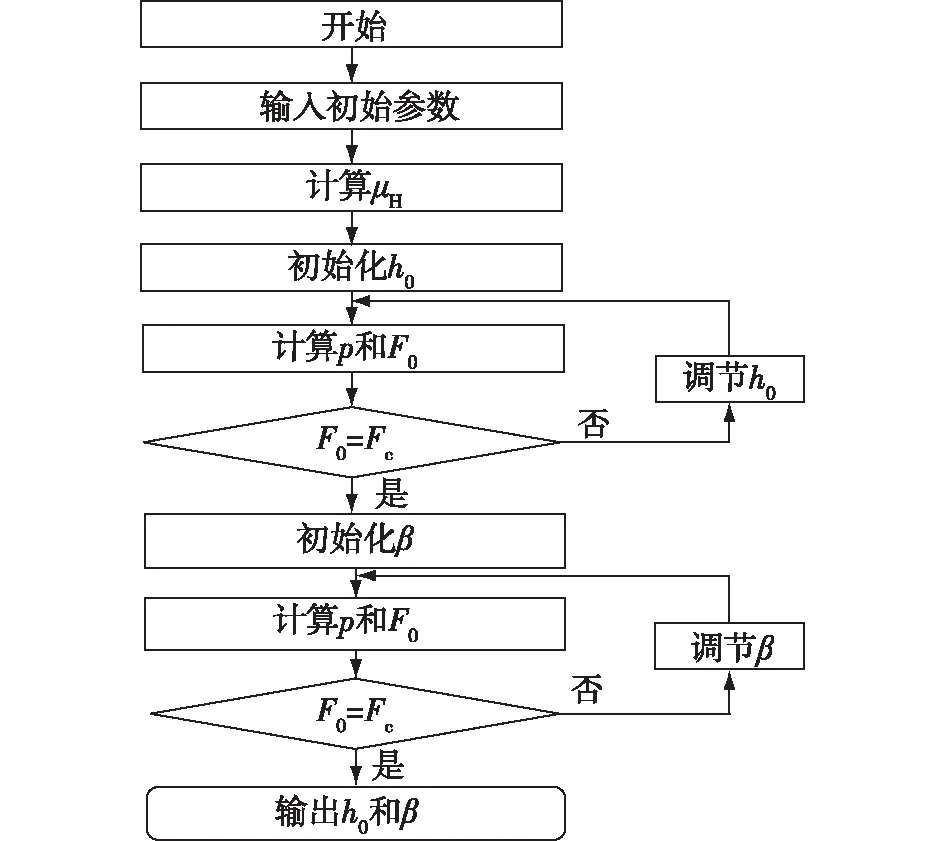
图4 密封环端面压力变形的计算流程Fig.4 Flowchart of pressure deformation generated by seal rings

5 结果与讨论

5.1 算例

磁性颗粒为Fe3O4,ρp=5 180 kg/m3,φ=6%,dp=25 nm,ar=1.03;基液为煤油,μ0=2.5×10-3Pa·s,ρ0=815 kg/m3。机械密封参数[4,10]:ri=34 mm,rg=43 mm,r0=52 mm,α=15,γ=0.5,槽长比(l)=0.7,hg=10 μm。I=0.6 A,TH=293 K,ω=200 rad/s,Fc=8 000 N,pi=101 325 Pa,p0=201 325 Pa。

5.2 密封环压力变形分析

5.2.1Fc和ω对pg、h0、β的影响

Fc和ω对pg、h0、β的影响见图5。由图5可知:在相同转速下,随着Fc的增大,h0减小,使密封端面磁流体膜压力增大,从而增大了F0,又抵消了Fc,密封环压力变形减小。在相同的闭合力下,随着转速的增大,磁流体动压效应增强,端面压力增大,F0增大,故h0、β增大。当h0较大时,密封端面压力降低,因此,端面磁流体膜压力实际增加不大。

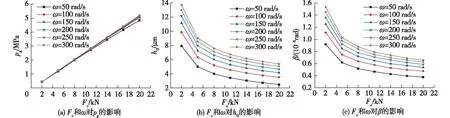
图5 Fc和ω对pg、h0、β的影响Fig.5 Effects of Fc, ω on pg, h0 and β

5.2.2I和p0对pg、h0、β的影响

I和p0对pg、h0和β的影响见图6。由图6可知:I对密封端面压力的影响不大,但I的增大使磁场的磁感应强度增大,从而加速了磁性颗粒的旋转速度、增大了磁性颗粒与基液的摩擦,使磁流体黏度增大,从而增大了F0,因此h0和β增大。p0对磁流体膜压力的影响较大,随着p0的增大,磁流体膜压力增大,螺旋槽的泵入效应増大,F0增大,则h0和β都增大。

5.2.3α和hg对pg、h0、β的影响

α和hg对pg、h0和β的影响见图7。由图7可知:当hg<10.0 μm时,随着α的增大,螺旋槽的泵入效应逐渐增强,pg增大;但继续增大α,螺旋槽的阻碍作用增强,由于损失了较多能量,因而pg又减小,因此,pg先稍增大后稍减小。而当hg≥10.0 μm后,磁流体平均膜厚过大,pg减小;随着α的增大,泵入效应增强,进入端面的磁流体增多,密封间隙增大,h0增大,较多的磁流体使得端面平均压力增大,开启力增大,因而β增大。

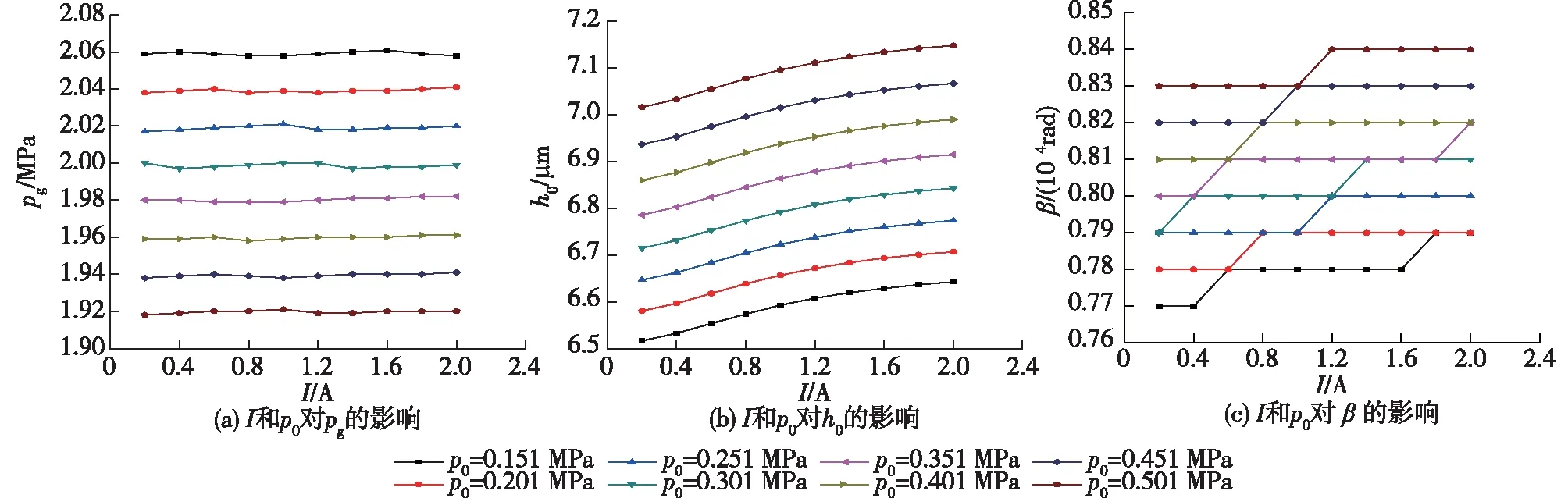
图6 I和p0对pg、h0、β的影响Fig.6 Effects of I, p0 on pg, h0 and β

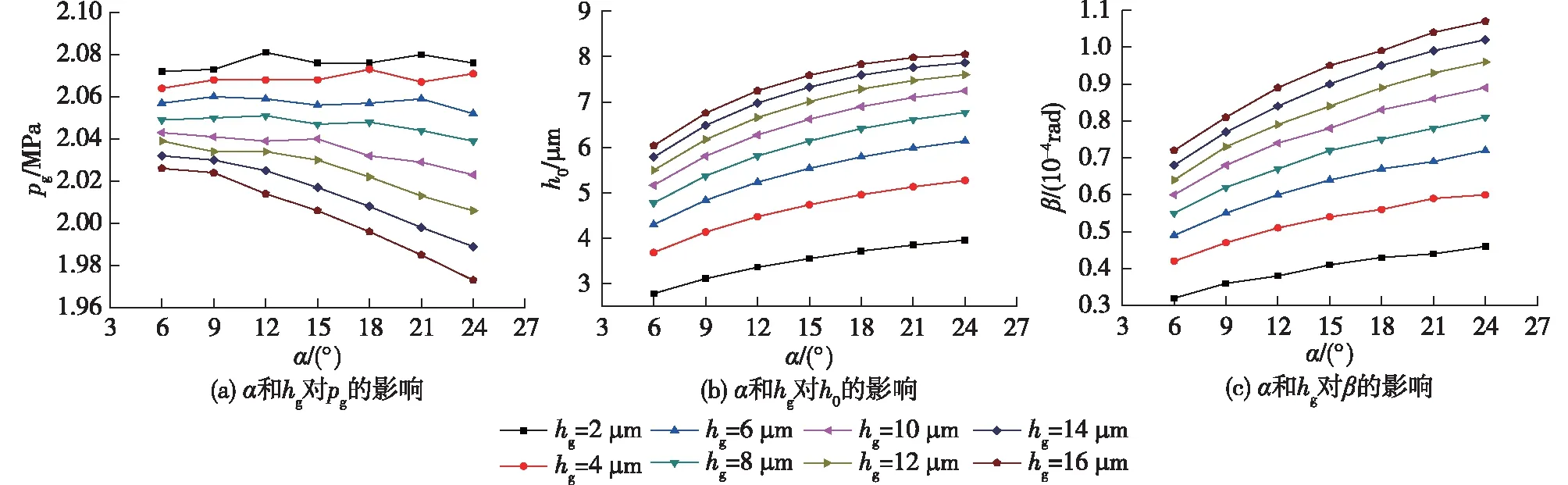
图7 α和hg对pg、h0、β的影响Fig.7 Effects of α, hg on pg, h0 and β

随着hg的增大,进入密封端面的磁流体增多,磁流体膜厚增加、pg减小、qm增大,h0增大；然而,较多的磁流体使端面平均压力增大,F0增大,β增大。

当γ接近于1时,对于干气密封而言，Gabriel[17]推荐hg=2.5～10.0 μm,α=10°～30°。由图7还可知:当hg<10.0 μm时,螺旋槽能产生较高、较稳定的动压效应,然而过小的hg(hg≤2.0 μm)又会使密封端面的摩擦加剧,当α>15°时,端面动压已开始降低。因此,本文推荐hg=2.5～10.0 μm,α=10°～15°。

5.2.4γ和l对pg、h0、β的影响

γ和l对pg、h0和β的影响见图8。由图8可知:随着γ的增大,螺旋槽宽度增大,磁流体流道变宽,则螺旋槽的泵入效应和阶梯效应增强,F0增大,h0增大;继续增大γ,螺旋槽阶梯效应减弱,F0减小,因而h0减小，因此，h0先增大后减小。

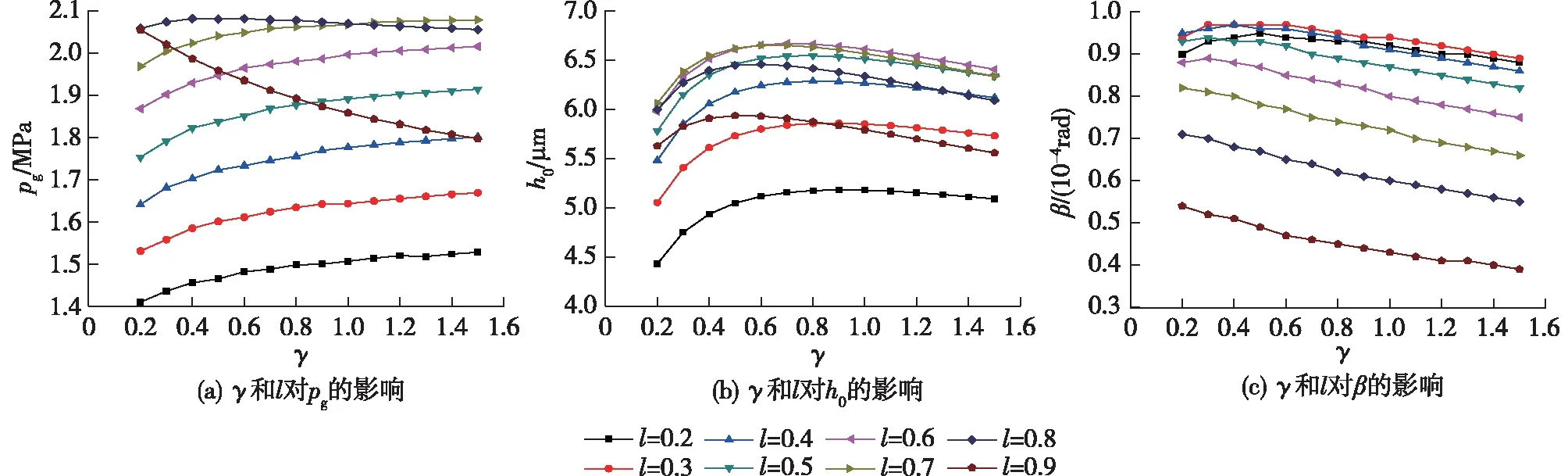
图8 γ和l对pg、h0、β的影响Fig.8 Effects of γ, l on pg, h0 and β

随着γ的增大,螺旋槽宽度减小,磁流体流道变窄,则螺旋槽的泵入效应增强,进入端面间的磁流体质量增加,pg增大,h0增大,这又导致端面平均压力减小,所以β减小。

由图8还可知:当0.7≤l≤0.8时,能产生较高且稳定的动压效应；在这一范围内,当l=0.8时,h0和β更小。因此,螺旋槽结构设计时,选择l=0.8为宜。

6 结论

1)推导了外磁场作用下磁流体润滑膜的黏度公式和磁流体密度公式,基于Muijderman窄槽理论,计算了磁流体润滑螺旋槽机械密封压力场和磁流体膜的开启力,根据受力平衡条件,计算了磁流体膜的厚度和密封环的角变形。

2)磁膜厚度和密封端面变形随着转速、密封介质压力、电流、槽深、螺旋角的增大而增大,随着堰槽宽比和槽长比的增大而先增大后减小,随着闭合力的增大而减小。

3)为了得到较高、较稳定的动压效应和较小的密封端面变形,应取槽长比为0.8，槽深为2.5～10.0 μm，螺旋角为10°～15°。