一种考虑系统不确定性估计的重载列车最优黏着控制

付雅婷，朱虹燕，杨辉

(1.华东交通大学 电气与自动化工程学院，江西 南昌 330013；2.江西省先进控制与优化重点实验室，江西 南昌 330013)

重载列车在铁路货物运输中起着重要作用，高牵引性能能使列车更好地运行，重载列车的牵引力由车轮和轨道之间的黏着力实现，黏着力由轮轨之间的黏着系数决定[1]。当轨面条件不好时，车轮的牵引转矩超过轮轨可提供的最大黏着力，会发生滑动或者空转现象，这种现象会造成轮轨磨损、列车牵引性能下降等不良影响，所以对重载列车的黏着优化控制研究具有重要的实际意义[2]。当前重载列车黏着控制主要分为2个方向，分别是再黏着控制和黏着优化控制，再黏着控制指的是在列车空转之后，使轮轨重回黏着状态的控制方法。传统的再黏着控制的主要方法是校正法，校正型系统的阈值设定要进行大量的实验研究，若参数调定不正确会影响机车牵引性能的发挥[3]。针对空转之后再黏着的问题，KONDO[4]提出了一种基于蠕滑加速度的再黏着牵引转矩指令生成方法，通过仿真计算验证了该黏着控制系统性能；PICHLIK等[5]利用无迹卡尔曼滤波估计黏着系数后再使用PI控制器实现再黏着控制。黏着优化控制则是以黏着特性曲线峰值点为目标，同时保持轮轨工作点始终位于黏着特性曲线的稳定区，其克服了校正法的不足，获得了相对更高的黏着利用率。近年来，关于黏着优化的控制策略取得了一定的成果。赵凯辉等[6]利用滑模极值搜索算法搜索得到黏着系数最优点，并设计超螺旋控制器来实现对列车最优黏着控制；ZHAO等[7]设计基于对称障碍李雅普诺夫函数的控制器对最优蠕滑速度进行跟踪控制实现最优黏着控制；李宁洲等[8]采用动态多子群GSA-RBF神经网络对重载列车进行黏着智能优化控制；WEN等[9]提出基于分布式模型预测控制的黏着优化控制。离散滑模变结构控制因为对系统的不确定性具有较强的鲁棒性，所以在计算机实时控制和工程上得到了较好的应用。但是离散滑模系统未进入滑模动态前，稳定性无法保证，针对此问题，提出将积分项引入离散滑模控制，其能够在系统开始运行时就抵消未知干扰的影响，增强了控制律的鲁棒性。段文杰等[10]将离散积分滑模容错控制用于含多故障的卫星控制系统中；郑长明等[11]针对永磁同步电机系统的不确定性和容易受到扰动影响的问题，提出离散比例-积分滑模控制，消除了稳态误差并实现了全程鲁棒性，得到了较好的效果。鉴于此，本研究针对重载列车安全平稳行车、提高牵引利用率的需求，提出基于离散积分滑模控制方法，对最优蠕滑速度进行跟踪控制，同时采用一步延迟估计方法对系统不确定性估计以此提高控制器的精确性。通过仿真结果验证，所设计的跟踪控制器能够对最优蠕滑速度进行精确快速的跟踪。

1 重载列车动力学模型和黏着特性

1.1 重载列车动力学模型

重载列车牵引系统可简化为重载机车轮对动力学模型和机车车体运动方程2部分。

忽略阻尼系数，牵引电机运动方程为[6]：

上述各式中，Tm为牵引电机输出转矩，N·m；TL为负载转矩，N·m；ωm为电机转子机械角速度，rad/s；ωd为轮对角速度，rad/s；r为轮对半径，m；vd为轮对线速度，m/s，vt为列车前进速度，m/s；vs为列车蠕滑速度；Jm为转动惯量，kg·m2；Fμ为轮轨间的黏着力，N；Rg为齿轮箱转速传递比；M为列车质量，kg；Fμi为第i轴牵引电机产生的牵引力，N；Fd为列车运行过程中的阻力，N，与车体速度vt相关；Wg为列车单轴轴重，kg；l，m和n为经验阻力系数，均为正常数。

1.2 轮轨黏着特性分析

列车在牵引过程中，轮对速度vd大于机车前进速度vt，定义蠕滑速度为轮对速度vd与机车速度vt之间的速度差，公式如下 ：

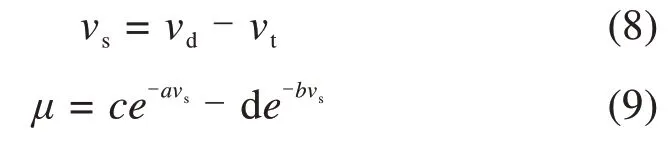
式中：a,b,c和d为轨面条件参数，均为正常数。

图1所示为3种不同轨面下的黏着特性曲线。由图1可知，不同轨面下的黏着系数是不同的，但在不同路况下都存在最大值，且随着蠕滑速度的增大黏着系数都呈现先增大后减小的趋势。峰值点左侧是黏着区，峰值点右侧是滑动区。在黏着区dμ/dvs>0，在滑动区dμ/dvs<0，在最大值处dμ/dvs=0。

图1 黏着特性曲线Fig.1 Adhesion characteristic curves

2 最优蠕滑速度参考值设定

2.1 观测黏着系数

轮轨表面的黏着系数无法直接测量，因此提出一种串联滑模观测器来观察黏着系数，在重载列车实际运行中，牵引电机的角速度ωm和转角θm是可测的，负载转矩TL不可测。通过对负载转矩的测量可以得到黏着系数的观测值[14]。

选择状态变量x1=θm,x2=ωm,x3=TL，根据式(1)，可以得到:

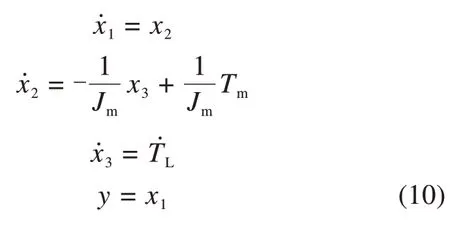
串联观测器公式如下：

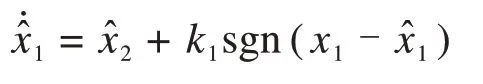
2.2 黏着特性曲线斜率估计

黏着特性曲线斜率估计值̂μ采用带有遗忘因子的最小二乘法(IRLS)进行估计，IRLS算法的更新规则可以表示为[15].

在式(16)中，γ为指数加权因子，P为误差协方差，λ为遗忘因子，φ(k)=dvs/dt，为了实时反映蠕滑速度的变化，需要对遗忘因子进行合适的设置，然后得到黏着特性曲线斜率的估计值

2.3 最优蠕滑速度搜索

使用梯度下降法自动迭代搜索蠕滑速度，得到最优蠕滑速度参考值。

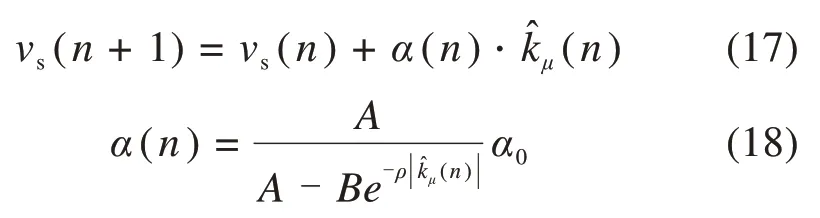
其中：α(n)是设计的自适应学习步长函数；α0为初始学习步长；A,B,ρ和α0都是需要设置的参数。

当黏着峰值点在黏着特性曲线左侧黏着区时，斜率̂μ为正值，根据式(17)，此时vs会逐渐增加接近峰值点，当在滑动区时，由于斜率̂为负值，vs会逐渐减小，当斜率̂μ=0时，搜索到最优蠕滑速度vs(n+1)=vs(n)。

3 最优蠕滑速度离散积分滑模跟踪控制器

3.1 重载列车最优黏着控制结构

重载列车最优黏着控制系统的结构如图2所示。图2包括串联滑模观测器、带遗忘因子的最小二乘算法、最优蠕滑速度搜索和离散积分滑模控制器4部分，首先牵引电机转子角度θm输入串联滑模观测器再经过式(7)得到实时黏着系数观测值，然后带遗忘因子的最小二乘法估计得到黏着特性曲线斜率̂μ，再使用变步长搜索算法对进行判断并搜索得到期望蠕滑速度v*s，最后离散积分滑模控制器根据实际蠕滑速度vs与给定期望蠕滑速度v*s之间的误差来计算控制输出牵引电机转矩T*m，从而达到重载列车最优黏着控制实现的目的。

图2 最优黏着系统控制框图Fig.2 Control block diagram of optimal adhesion system

3.2 对系统不确定性估计的离散积分滑模跟踪控制律设计

根据式(4)和式(5)，令x=vd-vt=vs，则重载列车模型可以转换为：

假设采样时间为T，利用前向欧拉法离散化式(19)描述的轮轨动态方程：

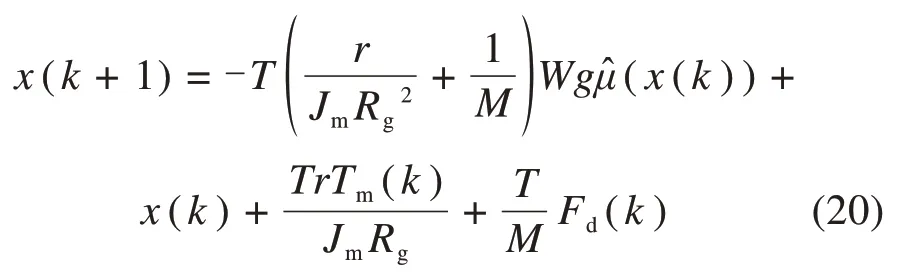
令u(k)=Tm(k)，将建模未考虑到的因素和离散化产生的误差称为系统不确定性̂(k)，则式(20)可以整理为：

首先，定义重载列车的离散蠕滑速度跟踪误差

式中：v*s(k)，vs(k)和e(k)分别为期望蠕滑速度、实际蠕滑速度及跟踪误差。

根据式(24)，定义离散积分滑模面[16-17]

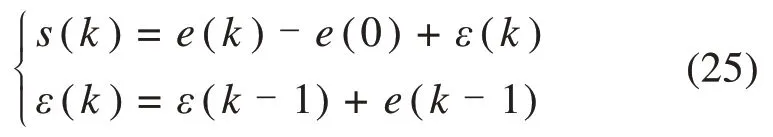
式中：ε(0)=0。

由式(25)可得

即系统状态从一开始就位于滑模面上，消除了滑模控制的趋近运动。

针对离散系统(21)，趋近律选择式(27)所示的离散指数趋近律。

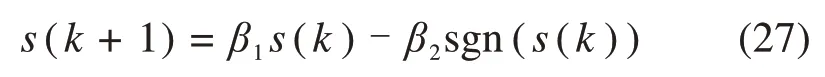
其中：0<β1<1，β2>0。

考虑式(25)滑模面，设计蠕滑速度离散积分滑模跟踪控制律为

式中：β1和β2为大于0的控制律设计参数。

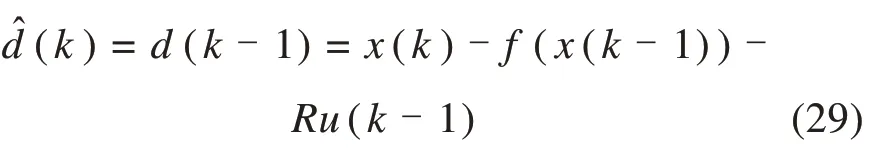
证明 将式(21)代入式(25)，可得

对于离散系统(21)，如果式(33)在所有时刻都成立，且β3>0，则由控制律(27)构成的闭环系统渐进稳定于期望蠕滑速度的附近。

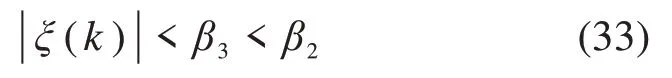
式中：β3>0为不确定性误差上确界。

根据式(32)，滑模面可分为以下几种情况。

当s(k)≥β2+β3时，可得

当s(k)≤-β2-β3时，可得

当采样时间T趋近于0时，系统不确定性误差上确界β3非常小，同时，由β3<β2可取β2为极小值。所以根据式(47)可以得知，控制律(28)构造的控制器能够使蠕滑速度渐进稳定在一个很小的区域，从而保证跟踪控制器的跟踪精度。

为了抑制式(28)中符号函数产生的抖振，采用饱和函数代替符号函数，则式(28)进一步修正为

式(49)中：τ为边界层厚度。

4 仿真分析

为了验证本文所提出的带有估计模块的离散积分滑模控制方法的有效性，本节对所提出的重载列车最优蠕滑速度跟踪控制策略进行仿真验证，并将其分别与经典离散滑模方法和无估计模块的离散积分滑模方法对最优蠕滑速度的跟踪效果进行对比，通过对比实验更好地体现了本文控制方法的优势。部分仿真参数见表1。

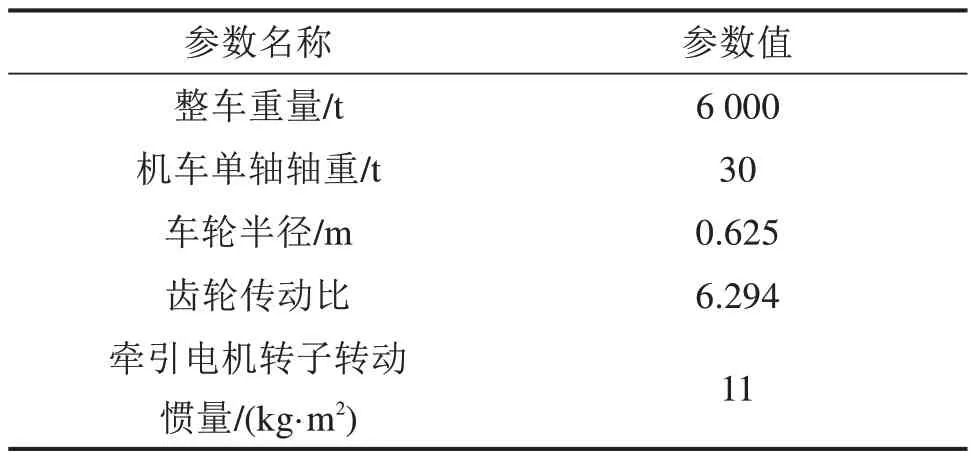
表1 仿真参数Tible 1 Simulation parameters

为了模拟轨面突变的情况，轨面状况采用图1所示的干燥、潮湿和雨雪3种状态，3种轨面黏着特性参数值如表2所示，首先重载列车运行在干燥轨面，于30 s时切换到潮湿的轨面状态，60 s时切换到雨雪的轨面状态，列车的阻力系数l=0.5，m=0.004 1，n=0.002 2，整个仿真时间为90 s，系统的采样和控制周期为0.1 s。

表2 黏着特性曲线参数值Table 2 Adhesion characteristic curve parameter value

串联滑模观测器观测黏着系数仿真结果如图3所示，红色和蓝色实线分别代表实际黏着系数和观测黏着系数，仿真结果表明观测器能够实现对实际值进行快速准确的估计。

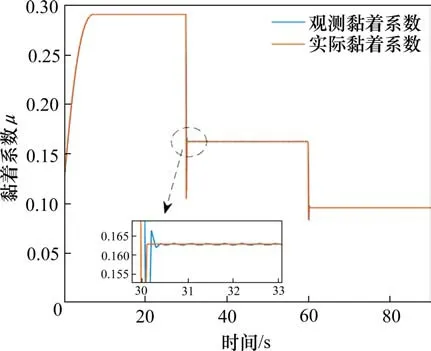
图3 黏着系数实际值与观测值Fig.3 Actual value and observed value of adhesion coefficient slip velocity tracking control

本文采用的带不确定性估计的离散积分滑模控制方法与采取经典离散滑模方法对期望蠕滑速度的跟踪效果对比如图4所示。由仿真对比结果表明：本文所提出的跟踪方法能够更精确地跟踪目标蠕滑速度，并且在变换路况的时候更加平稳。

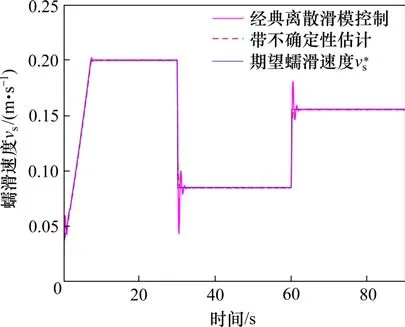
图4 带不确定性估计的离散积分滑模与经典离散滑模蠕滑速度跟踪控制Fig.4 Discrete-time integral sliding-mode with uncertainty estimation and discrete-time sliding-mode

为了验证带系统不确定性估计的离散积分滑模方法的优越性，将其与无不确定性估计模块的离散积分滑模方法进行了对比，仿真图如图5所示。从图5可以看出，由于最优蠕滑速度搜索算法的作用，每个路况下都搜索得到最优值，在30 s时干燥路面转变为潮湿路面，最优蠕滑速度从0.2 m/s降到0.085 m/s，在60 s时潮湿路面转变为雨雪路面，最优蠕滑速度从0.085 m/s增至0.153 m/s，无论离散积分滑模控制器带估计模块还是无估计模块，都能够稳定地跟踪目标蠕滑速度，但对系统不确定性进行估计的跟踪控制器具有更高的跟踪精度，跟踪误差如图6所示。同时根据图7显示的控制牵引电机转矩仿真情况，对不确定性进行估计的控制牵引电机转矩在转换路况时更加平滑，其具有更好的牵引平稳性。

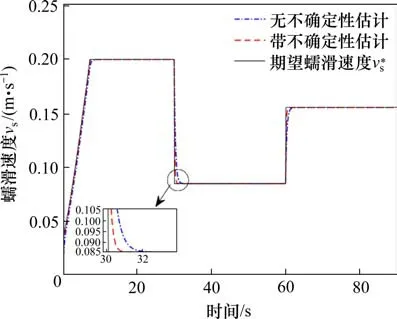
图5 带不确定性估计与无不确定性估计的离散积分滑模蠕滑速度跟踪控制Fig.5 Discrete-time integral sliding-mode with or without estimation tracking slip velocity

图6 带不确定性估计与无不确定性估计的离散积分滑模蠕滑速度跟踪误差Fig.6 Discrete-time integral sliding-mode with or without estimation tracking slip velocity error

根据图7牵引电机转矩仿真结果和图1黏着特性曲线，可以看出牵引电机转矩Tm和黏着系数μ随轨面状态变化的趋势总体一致，在0～30 s控制转矩Tm稳定于8 400 N·m，黏着系数观测值μ̂稳定在0.291附近,其与黏着系数实际值误差很小；在30～60 s牵引电机转矩Tm稳定在4 400 N·m，黏着系数观测值̂稳定在0.263附近，在60～90 s牵引电机转矩Tm稳定在2 300 N·m，黏着系数观测值μ̂稳定在0.095附近。仿真结果表明，即使改变2次路面状况，控制器也能及时调整牵引电机转矩跟踪上期望蠕滑速度，实现重载列车的最优黏着控制。

图7 带不确定性估计与无不确定性估计的离散积分滑模牵引电机转矩Fig.7 Comparison of traction motor torque discrete-time integral sliding-mode with or without estimation

5 结论

1)针对未知路面状况下的最优蠕滑速度参考值的选定问题，提出带遗忘因子的最小二乘算法和梯度下降法搜索得到最优蠕滑速度。设计离散积分滑模控制器跟踪期望蠕滑速度，使列车在轨面状态发生变化的情况下也能在较短时间内搜索到并稳定工作在最佳蠕滑速度下。

2)为了抑制抖振现象和提高控制系统精确性，设计一步延迟估计方法对系统不确定性进行补偿和估计。实验结果证明，所提出对系统不确定性进行估计的离散积分滑模控制器能确保较高的跟踪速度和精度，达到对重载列车最优黏着控制的要求。