基于改进HHO算法的城轨列车关键部件可靠性研究

周念玟，贺德强，苗剑，陈彦君，靳震震，刘力琼，徐伟倡

(1.广西大学 机械工程学院，广西 南宁 530004；2.南宁中车轨道交通装备有限公司，广西 南宁 530029)

随着我国城市化进程的加快，城市轨道交通列车数量剧增，列车关键部件的寿命预测不准确，会造成“过维修”或“欠维修”的情况，进而影响列车安全可靠运行。及时发现并更换易故障部件，可有效保障城轨列车的运营安全。可靠度是衡量列车关键部件是否需要检修的标准[1−2]。针对部件紧密连接、耦合复杂多变的列车系统，国内外学者建立了相应的列车系统可靠性模型[3−5]。由于单一化的故障数据处理往往与实际情况不符，为更准确判断故障率，需要对列车关键部件的运行可靠性进行更为深入的研究[6]。孟苓辉等[7]提出“亚安全”概念，对高速列车牵引传动系统建立了系统马尔科夫(Markov)状态转移模型；葛超等[8]利用图参数估计法和改进粒子群(Improved Particle Swarm Optimization,IPSO)算法求解列车车门系统三参数威布尔可靠性模型；沈国强等[9]利用图参数估计法和改进人工蜂群(Improved Artificial Bee Colony,IABC)算法求解机车车辆减振器三参数威布尔可靠性模型。YUAN等[10]利用分段威布尔分布求解列车转向架构架的载荷谱特征，建立可靠性模型。目前，国内外针对城轨列车关键部件的可靠性研究方法存在精度较低、通用性较差和计算量大的问题，忽略了实际过程中常见的数据丢失情况，缺乏对参数属性区间及权重的客观判断，容易陷入局部最优和不成熟的收敛缺陷。哈里斯·霍克斯优化(Harris Hawks Optimization,HHO)算法是一种新的基于种群、受自然群体智能启发的优化方法[11]，具有很强的参数敏感性，可以克服上述方法中精度低、不贴合实际等问题。本文在HHO算法的基础上添加一个循环检验过程，避免陷入局部最优，极大地提高了算法的收敛能力。运用改进的哈里斯·霍克斯优化(Improved Harris Hawks Optimization,IHHO)算法模型对列车车门系统和转向架系统的三参数威布尔可靠性模型进行参数评估，计算简单且可以快速、有效地预测列车关键部件的可靠性曲线，为后续基于可靠性的维修工作奠定基础。

1 可靠性分析及模型建立

1.1 威布尔分布模型

对于复杂系统，其可靠性曲线常为“浴盆曲线” ，其中退化失效是一个随时间延长而急速增加且不可逆的过程。三参数威布尔分布有很强的拟合能力，本文针对退化失效时期的可靠性，采用三参数威布尔分布函数评估列车关键部件的可靠度，其可靠度函数R(t)为：

其中：β为形状参数；η为尺寸参数；γ为位置参数；t为时间序列，且β>0，η>0，t>γ>0。

威布尔分布模型较为复杂，确定三参数十分困难[13]。针对超方程方法计算繁琐、运算量大的问题，本文采用图参数估计法求解参数，利用图形中故障数据点分布和渐近线分布求取威布尔三参数的初始估值(β0,η0,γ0)，如式(2)所示：

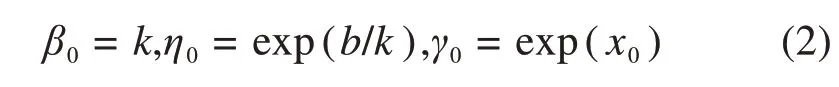
其中：k为斜渐近线的斜率；b为斜渐近线的截距绝对值；x0为垂直渐近线的横坐标。

在初始估值的基础上，引入宽松系数ρ(0<ρ<1)得到IHHO算法的搜索空间。

1.2 改进哈里斯·霍克斯优化模型

HHO算法是一种基于群体的、无梯度的优化技术。在探索阶段，老鹰根据同伴与猎物的位置随机栖息在几个地点，假设每个栖息策略都有相等的机会q，老鹰更新位置的表达式为：

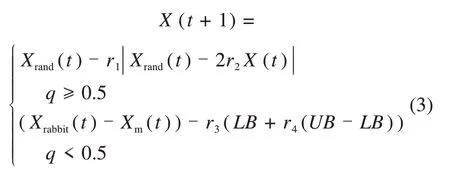
其中：X(t+1)为下一次迭代中鹰的位置；Xrabbit(t)为猎物的位置；X(t)为鹰的当前位置向量；Xrand(t)为从当前种群中随机挑选的一只鹰；Xm(t)为目前鹰派人口的平均位置；Xi(t)为迭代t次时每只鹰的位置；r1,r2,r3,r4和q为(0,1)的随机数；U B和LB为变量的上下界。

在开发阶段，根据老鹰追逐和猎物逃逸的行为，提出了IHHO算法的4种可能情况来模拟攻击策略，分别采用软围困、硬围困、软围困下渐进式俯冲和硬围困下渐进式俯冲的方式更新老鹰的位置。通过循环检验过程验证是否陷入局部最优，相关公式表达如下：

其中：ΔX(t)为迭代t时猎物的位置向量与当前位置之间的差；J为猎物在整个逃逸过程中的随机跳跃强度；E为猎物的逃逸能量；Y和Z为不同条件下鹰更新的位置；r为猎物在突袭前逃脱的机率；S为大小为1×D的随机向量；L F为莱维飞行函数[14]。

具体流程图如图1所示，其中，Dn为预测差值；Dn,α为临界差值。

图1循环检验过程中Dn的表达式如下：

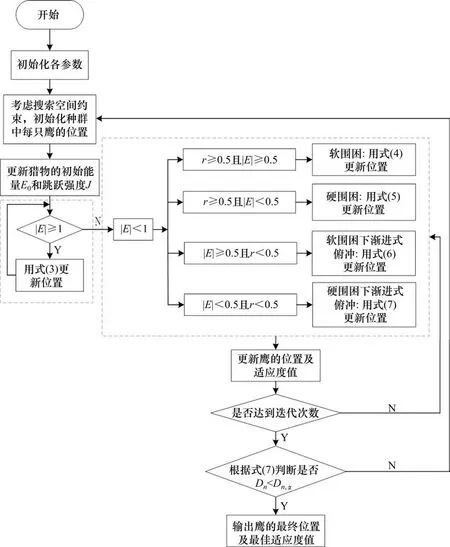
图1 IHHO算法流程图Fig.1 IHHO algorithm flow chart

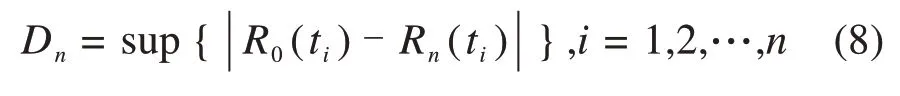
其中：R0(ti)为计算得出的每个故障数据的基于威布尔分布的可靠度函数；Rn(ti)为样本容量为n的经验分布的可靠度函数。

2 案例分析

2.1 故障数据分析

本文以某城市轨道交通2号线全部列车2019年3月至2020年3月的故障维修数据为研究对象，对列车一年内的故障数据进行整理和统计，统计结果如图2所示。其中，车门系统和转向架系统作为城轨列车的关键系统部件，其可靠性会直接对列车安全运行造成影响。本文选择这2个系统的故障记录为故障样本进行可靠性分析。根据帕累托法则选择车门系统和转向架系统的关键部件，即：车门系统客室门组件和下挡销组件、转向架系统轴箱组件和端盖组件，如图3所示。

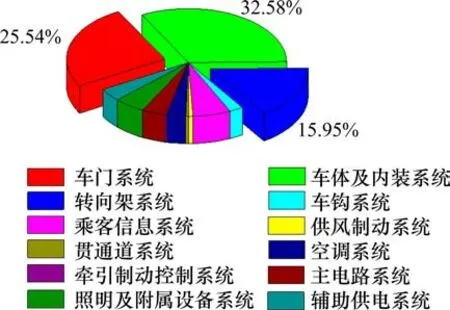
图2 故障数据统计Fig.2 Fault data statistics

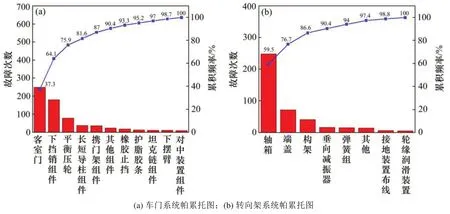
图3 车门系统及转向架系统帕累托图Fig.3 Pareto chart for door system and bogie system

2.2 IHHO算法的可行性分析

本文将图参数估计法计算得到的参数初值估值引入宽松系数ρ(0<ρ<1)，并代入IHHO算法的搜索空间中，利用IHHO算法寻找三参数威布尔模型中的参数最优值，实现列车关键部件的可靠度计算。其中，列车关键部件故障维修的样本数据通过定时截尾寿命试验获取，故障时间数据如表1所示，由于篇幅有限，仅展示部分数据。

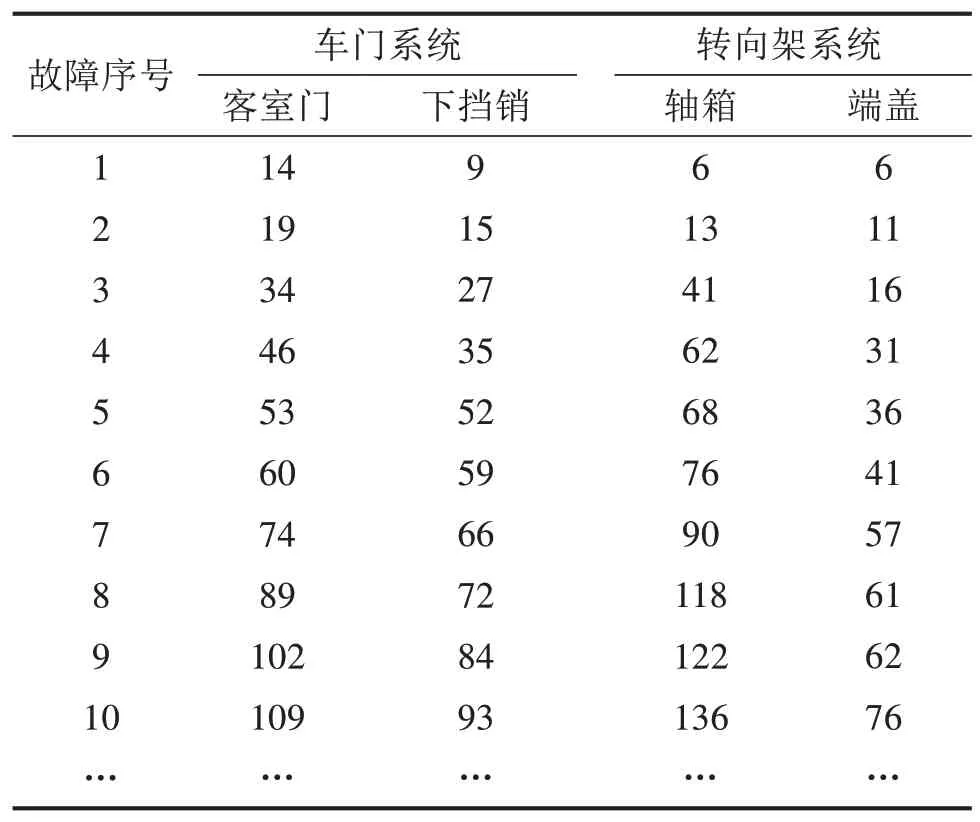
表1 列车关键部件故障时间数据Table 1 Failure time data of train key components

利用图参数估计法绘制各关键部件故障数据散点图及其渐近线，如图4所示，横坐标为预处理过的数据点，纵坐标为威布尔概率。图4中的散点具有明显的凹凸点，且呈曲线波动状，与三参数威布尔分布的特征相契合。根据散点的分布规律补充斜拟合直线和垂直渐近线，并取宽松系数ρ=0.7，利用IHHO算法对目标函数进行迭代寻优，得到车门关键部件及转向架关键部件的迭代过程。通过式(1)可得样本的似然函数L，并取自然对数得到目标函数，如下式所示：

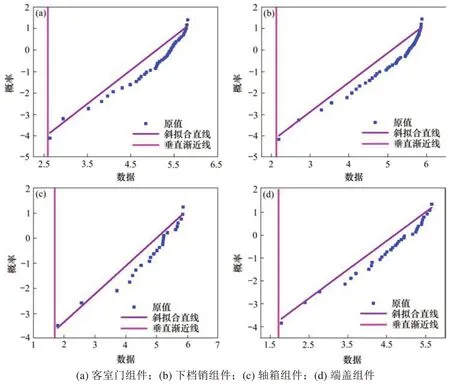
图4 车门系统和转向架系统关键部件威布尔概率Fig.4 Weibull probability of key components of door system and bogie system

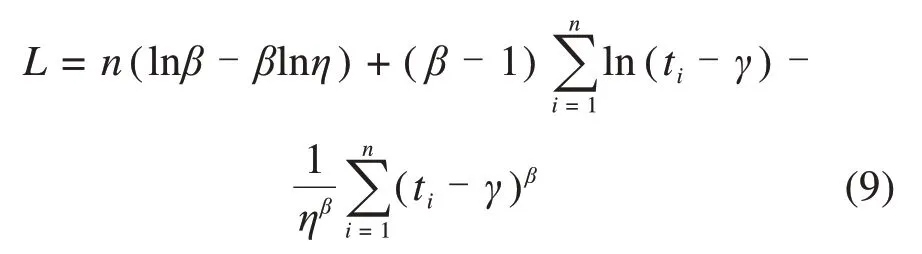
其中：n为故障数据样本数；ti为第i个时间序列故障样本点，i=1,2,…,n。

为验证IHHO算法寻得最佳适应度值的精度，选取各关键部件进行3次重复实验，作为在不同的随机搜索初始点下IHHO算法对列车各关键部件的迭代寻优曲线，如图5所示。其中，算法初始参数取值如下：目标搜索空间的维数d取3，迭代次数T取200，种群规模N取50。

从图5中观察到，IHHO算法的适用性强，能在极少迭代次数内达到关键部件的最佳适应度值，对于列车不同系统、不同部件的迭代效果相差小，具有强的通用性。算法可调参数少，在不同的随机搜索初始点下，测试的3条收敛曲线最快迭代速度有所不同，但影响较小，均在15次迭代以内完成迭代寻优过程，拥有收敛能力强和收敛速度快的效果。最佳适应度值浮动范围极小，寻优精度高。并且，对于车门系统客室门组件，其最佳适应度值浮动范围在0.1以内，下档销组件的最佳适应度值浮动范围在0.5以内；对于转向架系统端盖组件，其最佳适应度值浮动范围在0.01以内，轴箱组件的最佳适应度值浮动范围在0.03以内。因此，IHHO算法在列车关键部件可靠性分析中的表现优越，其可行性强。

图5 车门及转向架系统关键部件IHHO算法迭代3次寻优Fig.5 Iterative cubic optimization diagram of IHHO algorithm for key components of door and bogie system

根据计算结果，车门系统及转向架系统关键部件的威布尔分布模型最优参数和最佳适应度值如表2所示。

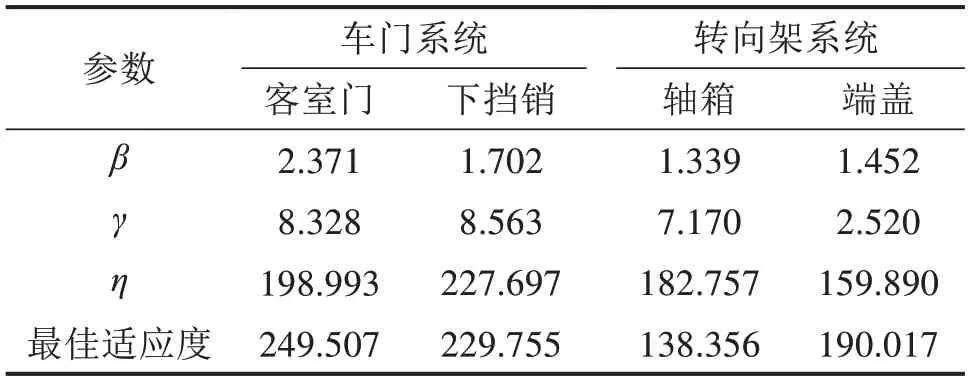
表2 车门系统及转向架系统关键部件最优参数及最佳适应度值Table 2 Optimal parameters and optimal fitness values of key components of door system and bogie system

3 结果分析

为验证IHHO算法对于解决参数估计问题的优越性，本文将与改进前的HHO算法、改进粒子群(IPSO)算法和人工蜂群(ABC)算法进行对比分析。

改进粒子群算法是一种模仿鸟类觅食的群体智能模型[15−16]，人工蜂群算法是一种模仿蜂群搜寻优良蜜源的群体智能模型[17]。运用HHO算法、IPSO算法及ABC算法对列车关键部件进行迭代计算，通过对式(9)中的目标函数寻优得到威布尔分布模型的参数估计值。为对比研究方便，HHO算法、IPSO算法和ABC算法的初始参数取值与IHHO算法保持一致，即目标搜索空间的维数d取3，迭代次数T取200，种群规模N取50，其余初始参数取值遵循经验公式[11,15,17]，本文不做过多阐述。同样对其进行3次重复实验，观察到不同的随机初始点对迭代速度存在一定的影响，其中，对IPSO算法影响最大，对HHO算法影响最小。选择精度效果较好的迭代过程进行展示，如图6所示。

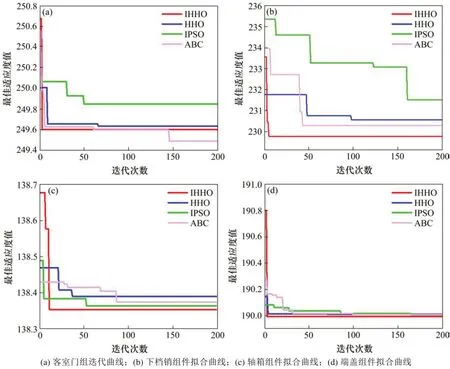
图6 车门系统及转向架系统关键部件各算法迭代对比Fig.6 Iterative comparison of algorithms for key components of door system and bogie system

由图6可知，IPSO算法会过早陷入局部最优，寻优能力弱，收敛速度慢，无法对数据量较杂的客室门组件和下档销组件进行合理寻优，无法进行有效的可靠度预测。ABC算法的收敛能力不强，收敛速度较慢，容易陷入局部最优，对不同的列车关键组件的寻优过程极不稳定，通用性较差。HHO算法的收敛速度和收敛能力强于IPSO算法和ABC算法，但容易陷入局部最优，收敛不成熟。

根据各算法预测的三参数威布尔模型和实际故障数据绘制列车关键部件在各算法下的可靠度衍变曲线，如图7和图8所示。

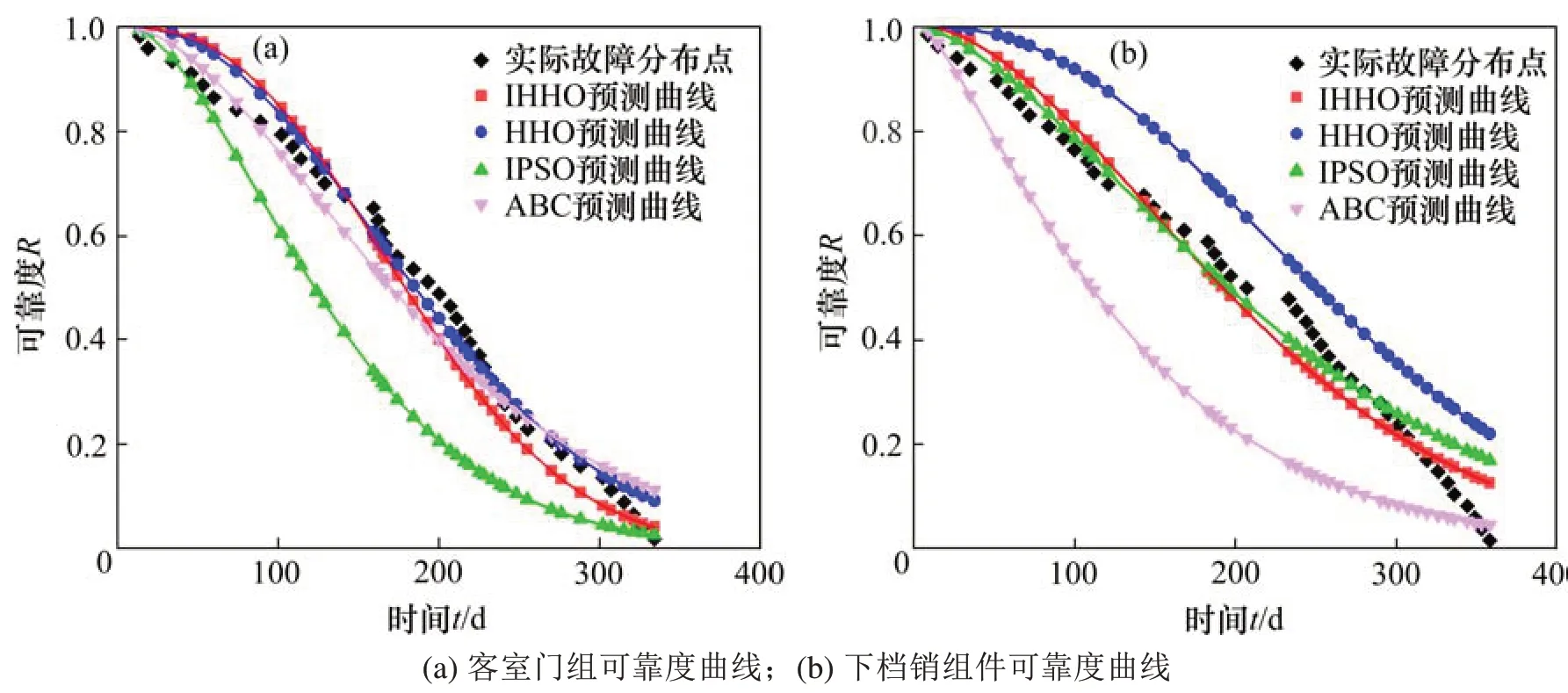
图7 车门系统关键部件可靠度曲线Fig.7 Reliability curves of key components of door system

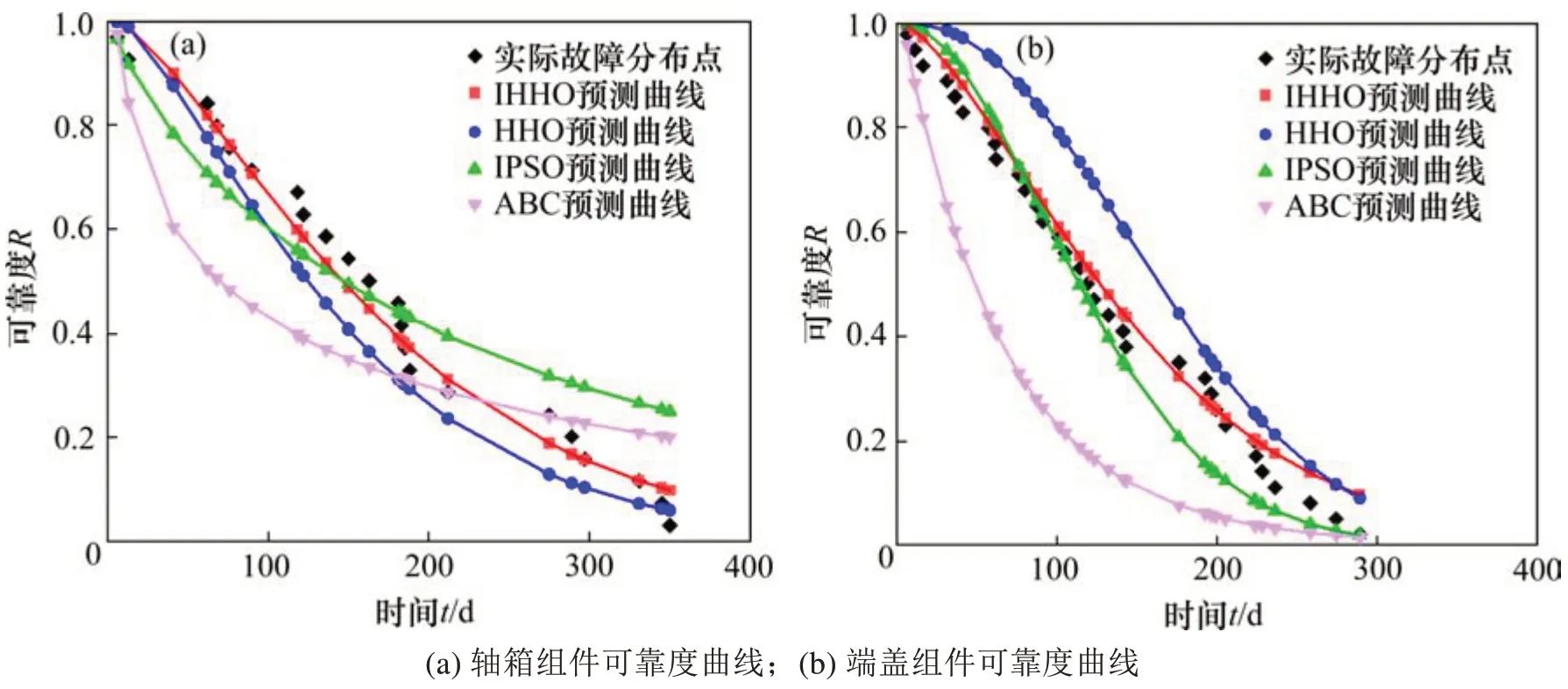
图8 转向架系统关键部件可靠度曲线Fig.8 Reliability curves of key components of bogie system

观察图7，通过IHHO寻优后得到的可靠度曲线与实际故障数据拟合良好，预测的可靠度曲线在早期故障时略高于实际故障数据，说明对早期可靠度预测存在一定的误差。随着时间的变化，预测的可靠度曲线逐渐与实际故障分布贴合，并随着时间的推移低于实际故障分布，说明在达到一定的数据量后IHHO算法对后期拟合趋势进行修正；通过HHO算法寻优后得到的客室门组件可靠度曲线基本贴合实际故障分布，下档销组件可靠度曲线高于实际可靠度；通过IPSO算法寻优后得到的客室门组件可靠度曲线低于实际可靠度，下档销组件可靠度曲线基本贴合实际故障分布；通过ABC算法寻优后得到的客室门组件可靠度曲线基本贴合实际故障分布，下档销组件可靠度曲线基本贴合实际故障分布。观察图8，通过IHHO寻优后得到的可靠度曲线与实际故障数据十分贴合，预测曲线在实际故障分布点上下略有浮动，说明IHHO算法在转向架系统关键部件上具有很强的有效性。通过HHO算法寻优后得到的可靠度曲线在实际故障分布上下浮动；通过IPSO算法寻优后得到的可靠度曲线适用性较好；而通过ABC算法寻优后得到的可靠度曲线均低于实际故障分布。

分析图7和图8，通过IHHO算法寻优后的预测曲线的预测精度差小，基本贴合实际故障分布规律，因此，本文提出的方法在列车关键部件的可靠度预测方面具有高的可行性。而HHO算法、IPSO算法和ABC算法寻优后的可靠度预测曲线适用性和通用性均较差，可靠度曲线与实际故障分布存在较大的出入，不贴合实际故障分布规律。关键部件的可靠度是衡量是否进行维修的重要指标，本文得到的可靠度曲线，为预防性维修提供理论参考，为后期列车关键部件维修管理做好充分准备。

将4种算法计算的可靠度预测曲线与实际故障分布进行对比，由式(7)求各算法预测精度并取平均值，平均预测精度差如图9所示。

图9 各算法平均预测精度差对比Fig.9 Comparison of average prediction accuracy difference of each algorithm

观察图9，IHHO算法得到的平均预测精度差较小且平稳，而HHO算法、IPSO算法及ABC算法的平均预测精度差起伏大，说明预测曲线不稳定，与实际故障分布曲线不贴合，不适用于列车的可靠度预测研究。具体平均预测精度差值如表3所示。

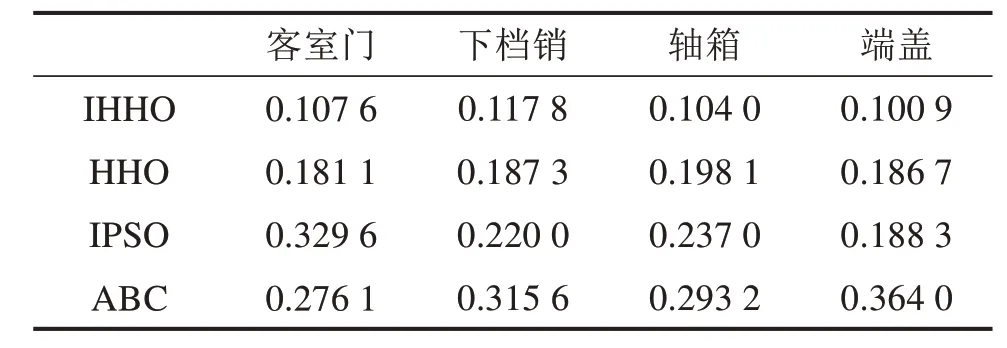
表3 各算法平均预测精度差值Table 3 Average prediction accuracy difference of each algorithm

各算法迭代速度如表4所示。由表4可知，IHHO算法的迭代时间相较于IPSO算法和ABC算法平均分别缩短了15.20倍和3.72倍，与HHO算法的迭代速度相差较小。

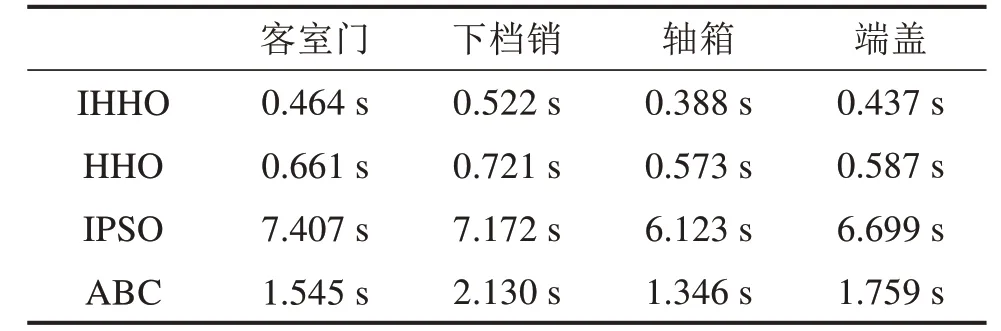
表4 各算法迭代200次速度对比Table 4 Speed comparison of 200 iterations of each algorithm

综上，使用IHHO算法对列车关键部件进行参数估计，可以对参数进行较为精准的估计。相对IPSO算法、ABC算法和HHO算法，IHHO算法收敛能力更强，收敛速度更快，预测精度差更小，适用于建立列车关键部件的可靠性模型。

4 结论

1)对哈里斯·霍克斯(HHO)算法进行了改进，提出了基于IHHO算法的列车关键部件可靠性参数估计方法，且算法的可调参数较少，能快速有效地寻找最优参数，证明了IHHO算法对列车关键部件可靠度预测的可行性。

2)以列车车门系统和转向架系统的关键部件为例，得到了与实际可靠度曲线相贴合的预测曲线，拟合程度高，证明了IHHO算法对列车关键部件可靠度预测的有效性。

3)与改进粒子群(IPSO)算法和人工蜂群(ABC)算法相比，本文提出的IHHO算法在可靠度参数估计中更有优势，收敛能力更强，收敛速度更快；与HHO算法相比，本文提出的IHHO算法在可靠度参数估计中精度更高。