大学生引体向上练习的优化模型建构

刘旭光 冯心怡 张雅男

(南京信息工程大学，江苏 南京 210044)

引体向上是克服自身重量的一种力量练习方法和能力，其锻炼价值高，通过练习，能够增强人的上肢肌肉力量、悬垂和攀爬能力，在生活中有很高的实用价值[1]。它是衡量男性上肢力量素质的重要参考标准，因此一直作为中学和大学男生的测试项目之一。引体向上的动作发力主要是依靠胸大肌、背阔肌和肱二头肌(包括肱肌和肱桡肌)的肌肉力量。长期练习引体向上，不仅可以通过锻炼胸大肌、背阔肌和肱二头肌来拥有健美的体型，且在控制体重、矫正因久坐而引起的各种脊柱问题和提高心肺功能等方面也具有一定的帮助[2]。

但在实际的体育教学中，由于学生体态、力量等诸多因素，引体向上一直是我国中学与大学男生最为薄弱的项目，许多学生甚至无法独立完成引体练习。表1是2020年和2021年江苏省南京籍大学一年级新生引体向上成绩[3]，表2是广西某高校2019年体质测试抽测的引体向上成绩[4]。表3列出我国高校男生引体向上的评价标准。从上述列举的数据可知，我国男生引体向上成绩普遍较弱，无法达到基本要求。对此，专家学者给出了许多有助于提高引体向上成绩的技巧与方法。如：江玉芬在《有效提高高中男生引体向上成绩的方法研究》[5]一文中，提出可通过大小臂多角度悬垂、弹力带下拉、单杠划船等辅助动作来体会发力从而帮助引体向上的练习;冯鹏在《“引体向上”的学练方法探讨》[6]中提出通过针对性的辅助训练来逐渐提升上肢及肩带力量，并制定了训练方法，帮助学生从易到难、循序渐进来增强上肢肌肉群力量，从而提高引体向上成绩。

表1 2020、2021 年江苏省南京籍大学一年级新生引体向上等级情况统计表

表2 广西某高校男生体质测试抽测引体向上成绩

表3 国家学生体质健康标准(大学男生引体向上)

此类文章一般是由从事多年体育教学的工作者，根据其教学经验提出训练方案。他们尝试改变传统的训练方法，提倡通过循序渐进并兼顾多样性和趣味性的方式来帮助学生提高引体向上成绩。该方法具有一定的实践意义，但是往往是以说教的形式阐述，凭借经验总结给出方法，缺乏理论证明，没有科学依据[7]。笔者查阅文献，发现很多运动项目的研究，已与现代化技术相结合，从而得出更为科学的结论来指导和改进运动方案。因此，笔者与物理专业学生组成团队，从生物力学模型出发，研究引体向上过程中的肌肉发力做功、发力变化和肌肉“冲量”等情况，并且通过数值求解矩阵进行优化，最后利用Adam算法给出引体向上过程中的最优策略，从科学的角度为学生在练习引体向上的实践中提供一些参考。

1 研究对象与方法

1.1 研究对象

本研究以大学生引体向上练习的优化模型构建为研究对象，以某大学一年级新生为实验对象，根据实测数据建模计算，分析计算结果，得到最优策略。被测试者体重为70kg，身高为1.75 m，测试期间，平均可做引体向上个数为5个。

1.2 研究方法

1.2.1 牛顿定律

牛顿第一定律：任何物体(质点)如果没有受到其他物体的作用，都将保持静止或匀速直线运动状态，即：物体如果不受其他物体的作用，它的速度将保持不变。

牛顿第二定律：当某一物体(质点)受到外力作用时，该物体所获得的加速度和外力成正比，和物体本身的质量成反比，加速度方向和外力的方向一致。其数学表达式为

(1)

1.2.2 质点系动量定理与质心运动定理

质点系的动量定理：

质点系的动量为

(2)

则其动量定理为：

(3)

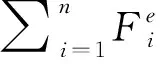
质心运动定理：

质心，即质点系的质量中心，它是质点系中恒存在的一个特殊点，它的运动很容易被确定。分析问题时，取用质心为参考系，有时可使问题大大简化。

质心的位置按如下定义确定：假设有n个质点，它们的质量是m1,m2…mn位于P1,P2…PN诸点，这些点对某一参考点O的位矢是r1,r2…rn则质心对此同一点的位矢rc满足如下关系：

(4)

由上式，可知

(5)

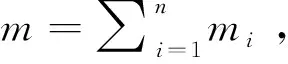
(6)

其中vc是质心的速度，由质点系动量定理可得

(7)

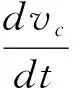
1.2.3 冲量

力和力的作用时间的乘积(力为常量)或力对作用时间t的积分(力为变量)

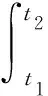
(8)

1.2.4 刚体定轴转动定律

刚体是一种特殊的质点系，该质点系中任何两个质点间的距离，不因力的作用而发生改变。

它是一种抽象、理想的模型，在所研究的问题中，当物体的大小和形状变化可以忽略不计时，可以将其视为刚体。

刚体的运动一般分为平动、定轴转动、平面平行运动定点转动和一般运动。在本模型的受力中，我们将运用刚体定轴转动的相关理论来进行分析。

力矩：力F对空间某点的矩。若F为作用在B点的力，则F对于另一定点A的力矩定义为

M=r×F=rFsinθ

(9)

其中r为B点对A点的位矢,θ为r和F间的夹角。

动量矩：动量对空间某点的矩。B点上的动量p对另一定点A的动量矩定义为

J=r×p=rpsinθ

(10)

若刚体绕z轴转动，由固定轴的动量矩定理知：

(11)

其中Jz是刚体对z轴的动量矩。Mz是刚体对z轴的力矩。即刚体对某一固定轴的力矩等于其对定轴动量矩的时间微分。

刚体绕固定轴的转动定律表示为：

Mz=Izzβ

(12)

其中，β是刚体绕定轴运动的角加速度，Izz为刚体绕z轴的转动惯量，其定义为

(13)

刚体的形状、质量分布以及固定轴确定后，刚体绕定轴运动时的转动惯量为一常量。

当选取过质心的轴为定轴时，转动定律改写为

Mc=Icβc

(14)

其中βc和Ic分别就是刚体绕质心转动的角加速度和转动惯量。[8]

1.2.5 蒙特卡洛方法

蒙特卡洛方法是指，当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。

蒙特卡罗方法的解题过程可以归结为三个主要步骤：构造或描述概率过程；实现从已知概率分布抽样；建立各种估计量。

使用蒙特卡洛方法求解问题，首先要构造或描述概率过程，实现从已知概率分布抽样。最后，建立各种估计量。一般说来，构造了概率模型并能从中抽样后，即实现模拟实验后，就要确定一个随机变量，作为所要求的问题的解，称之为无偏估计。建立各种估计量，相当于对模拟实验的结果进行考察和登记，从中得到问题的解。

1.3 模型的建立

1.3.1 Adam算法的起源

Adam(Adaptive Moment Estimation)是深度学习中的一种随机梯度优化算法。深度学习是指机器学习样本数据的内在规律和表示层次，以达到能够像人一样具有分析学习和识别文字、图像和声音等数据的能力。[9]深度学习的模型中往往含有大量参数，为了修正这些参数，人们提出了许多的优化算法。其中包括Adam算法在内的一阶优化算法，主要是通过目标函数的梯度或梯度的无偏估计来更新模型参数不断迭代从而达到逼近目标函数的最优值的目的。[10]

Adam利用梯度的一阶矩估计值和二阶矩估计值来动态地调整每个参数的学习率，本质上是带有动量项的Adagrad，故而结合了均方根传播(RMSprop)算法和适应性梯度(AdaGrad)算法的优势。

适应性梯度(Adagrad)算法是为每一个参数保留一个学习率以提升在稀疏梯度(即自然语言和计算机视觉问题)上的性能。均方根传播(RMSProp)是基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。而Adam算法不仅如RMSProp算法那样基于一阶矩均值计算适应性参数学习率，它同时还充分利用了梯度的二阶矩均值(即有偏方差)，[11-12]并且经过偏置校正，使得每一步的有效学习率都在一定的范围内变动。

1.3.2 动力学分析

Adam算法的动力学分析如下，下式是梯度的一阶矩估计值和二阶矩估计值，它们是以移动平均值的形式表现：

mt=β1mt-1+(1-β1)gt

(15)

(16)

其中，mt是有偏置的梯度一阶矩估计值，vt是梯度的有偏二阶矩估计值，gt是第t步的一阶梯度。β1和β2分别是梯度一阶矩估计值(mt)和二阶矩估计值(vt)的指数衰减速率，也可称为动量系数和自适应学习系数，其值范围是：β1，β2∈[0,1]。[13]其中系数β1控制着动量的大小，其值设置需要权衡加速收敛和稳定性。当其越接近1时，加速效果越好，但与此同时，动量将变得很大，参数更新方向将仅仅依赖于最近几个随机梯度，可能会发生震荡。为了使每一步的有效学习率都在一定范围内变动，参数的计算更平稳，故需计算更正偏置后的梯度一阶矩估计值和二阶矩估计值：

(17)

(18)

Adam的更新规则为：

(19)

其中，η是Adam算法的步长，θt和θt+1是第t步和第t+1步的权重值[10]。

综上而言，Adam算法善于处理稀疏梯度且对内存需求较小，为不同的权重参数分配不同的自适应学习率，适用于大多非凸环境的优化，比如神经网络，同时适用于高维空间和比较大的数据集，是目前最流行的算法。[13]本文中的模型，计算时包含多个参数，若使用传统的求导来计算极值，无疑十分复杂，故而选择使用Adam算法，虽然计算时间稍慢，但计算结果更为精确。

1.3.3 根据算法建立模型

一个标准的引体向上包括预备姿势和动作阶段两个过程。预备姿势时，双手位置与肩同宽固定于单杠上,上肢伸直, 肩胛骨处于上旋位, 躯干与下肢处于悬垂,身体处于相对静止状态。而动作阶段又分为拉引和还原两个环节。在拉引过程中，上臂应在肩关节处后伸, 稍内收, 拉躯干靠近臂, 同时肘关节屈曲, 上臂肘关节处靠近前臂, 变直臂悬垂为屈臂悬垂, 将人体拉近握点, 身体保持垂直上升, 使横杠在胸部位。还原过程中，躯干离开上臂, 同时上臂在肩关节处屈, 肘关节伸, 变屈臂悬垂为直臂悬垂, 使人体下降回到预备姿势。由于下降动作方向与重力方向一致, 拉引动作与重力作用方向相反, 故引体向上的主要作用在第一环节。[14]

现根据对引体向上发力关节及动作要领，采用了铰链[15]手臂模型对其进行分析。模型示意图如图1所示。以A、D为活动节点，BC,CE,BE代替手臂弯曲时肌群(如肱二头肌、肱三头肌)，不论在压缩时还是拉伸时均可根据情况产生拉力或者推力，使手臂发生转动。

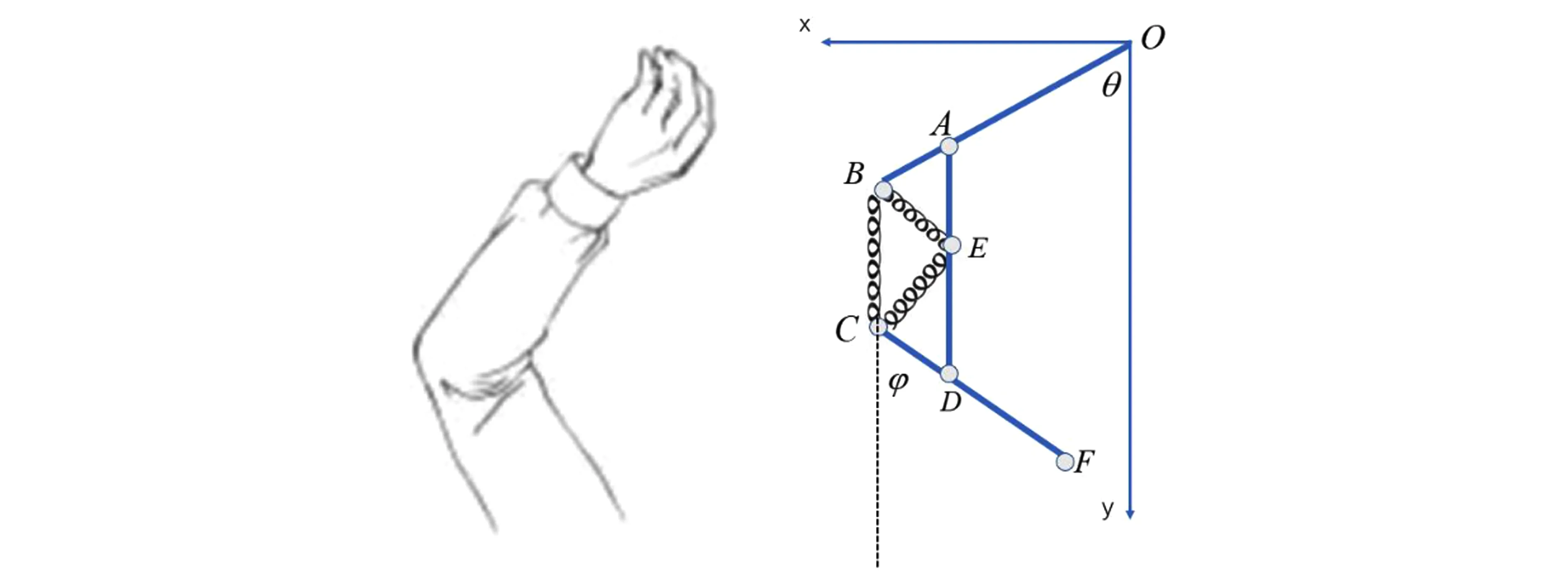
图1 铰链模型示意图

为了简化模型，本文作如下假设：

a)假设OB，CF为质量均匀分布的刚体，AD为忽略质量的刚体。

b)在规定的xOy坐标系中，AD始终与y轴平行。

c)代表肩膀处肌群的BC,CE,BE三块肌肉不会弯曲，但会如弹簧一般伸长收缩，且只能发出延自身方向的拉力或者弹力。

d)节点A，B，C，D，E在运动时均无摩擦力。

模型中符号较多，因此在表4进行统一规定。

表4 符号规定

1.4 模型的求解

引体向上动作图如图2(a)所示，手臂与肩膀连接处会受到躯干因重力而产生的向下的拉力，对应受力模型中为F点所受的重力。手掌与器械接触部位会有器械给予向上的支持力，对应受力模型中，O点会受到向上的支持力[16]。据此，可以给出等效受力图，如图2(b)。

(a) (b)图2 (a)引体向上动作图(b)等效受力图

以正手引体向上为例，动作分为垂吊、躯干向上运动和躯干向下运动3个环节。本文只分析躯干向上运动过程中的肌肉发力情况。躯干向上运动时，肱桡肌、肱二头肌、胸大肌、背阔肌等肌群共同的收缩产生力量，克服自重将身体往上拉起，当下颌超过单杠时方可向下还原[7]。根据等效受力图可以进行受力分析，刚体CF、AD、OB所受合外力为零，由质心运动定理可知，其质心所受合外力即为零，故质心无加速度及角加速度。分别取其质心为转轴，由转动定理知质心的合外力矩为零。应用牛顿定律以及刚体定轴转动定律列出下列方程：

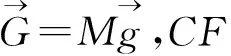
(20)

CF以D点为定轴转动点，应用转动定律可以得：

(21)

同理，对AD列出受力方程：

(22)

AD以E为定轴转动点，应用转动定律得到：

(23)

对OB列出受力方程：

(24)

OB以O为定轴转动点，应用转动定律得到：

(25)

为了能够进行仿真计算，表5中给出了各点的坐标表达式。

表5 各点坐标

1.5 模型的数值计算

上述给出6个方程，需要联立为线性方程组才能求解，但方程中给出的是矢量，因此，将方程中的矢量转换为标量，转换关系如下表：

表6 力的矢量与标量转换关系

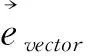
表7 方程组系数矩阵

利用计算机求解上述九元线性方程组，可以得到某一时刻，给定θ,φ时各肌肉的发力情况，根据不同解讨论引体向上最优策略。

2 引体向上最优策略研究

2.1 引体向上完成的限制条件

一个正规的引体向上的完成条件是手臂完全下垂，拉动手臂至下巴经过杠杆。本文不考虑下身辅助动作，只分析手臂发力对完成动作的影响。引体向上动作开始时：

θ=0,φ=0

(26)

结束时：

ADcosθend+DFcosφend≤H

(27)

上式中，H为肩膀距离单杠的规定高度，θend,φend为结束时的θ,φ值。

2.2 引体向上评价指标的选择

做引体向上时，人会感觉到肌肉的疲劳，但并不能明确地描述做功情况。本文的模型中，将其简化，假设θ,φ均为先匀加速变化，后匀减速变化，角速度分别为ω1,ω2，且开始时与结束时θ,φ的角速度均为0。

加速阶段的加速度大小分别为α1,β1，减速阶段的加速度大小为α1，β2。且当θend,φend确定时，根据运动学定律，可以得到θ,φ的加速时间t1,t3，减速时间t2,t4有以下关系：

α1t2-α2t2=0

β1t3-β2t4=0

(28)

通过上述方程组(29)即可解出t1,t2,t3,t4。

结合肌肉的发力情况，定义肌肉发力“冲量”为：

(29)

做功为

(30)

三块肌肉力的最大瞬时变化为：

(31)

将上述物理量代入前文模型，求解模型中BC，BE，CE收缩做功，即人体完成引体向上时总冲量I与总做功W。将其优化得到最优结果，即最小值。

经过计算发现，当完成引体向上的个体确定后，总做功相同，则只需讨论总冲量。给出优化目标与限制条件：

(32)

优化自变量：α1,β2,α2,β2,θend,φend

本文使用蒙特卡洛方法[17]随机将α1,β1,α2,β2,θend,φend赋值，寻找满足约束条件且其中Isum与V的最小值λ1,λ2，且规定优化变量为比例之和，即：

(33)

这样可以确保优化过程中η最小，即可求得最优的Isum,V。

2.3 使用Adam算法优化求解

本模型中使用Adam算法，通过调整各个参数值，来获得目标函数的最优值。因此，采用Python的Pytorch库中的Adam算法对上述模型进行优化求解。

带入某一时刻测试学生的情况(见表8)，带入模型计算。

表8 测试者情况

2.4 最优结果及分析

通过2.3算法得到完成引体向上的最优结果模型，见表9：

表9 算法优化求得最终结果

由测试者的数据及上述模型和Adam算法求出的最终解，可知在平时训练学生完成引体向上动作时，应保持加速阶段的加速度大小分别为0.0631和0.1911(rad/s2)；减速阶段加速度大小分别为0.0445和0.1633(rad/s2)；且将引体向上过程中最终的θend,φend控制在0.13rad，1.43rad时，肌肉发力会有最小的冲量和最小的瞬间力变化，对于测试者更加省力。简单来说，若一名体重70kg，身高1.75m的学生，其臂展也为1.75m。做引体向上需要通过手臂将身体向上提高的高度大约在55-65cm。根据本文提供模型计算得到结果，引体向上动作完成时，小臂与竖直向下方向的夹角不能超过7.5度，而大臂与躯干之间的夹角不能超过82度，这样可以保障肌肉发力最高效，更有利于学生完成引体向上。若训练者身高、体重发生变化，则可根据模型重新计算，得到新的适合训练者本人的数据。

本文通过生物力学铰链模型的数值计算，结合实际条件，给出了优化完成引体向上的方法，该方法可代入训练者自身条件的具体数值，从而快速求解完成引体向上动作的最优解，尤其是动作结束时的角度，这样更加科学合理地指导训练者训练。体育运动不能完全倚靠数据来进行锻炼，提高引体向上成绩，需要肌肉力量的增长和肌肉横断面积增大、神经调节功能改善、肌纤维数量增多等生理变化，这一过程需要长时间的锻炼，逐步积累，但通过物理模型计算得到的数据，可以更有效地指导训练，更高效地完成动作，对日常练习和提高训练效果提供了一种参考方法。