改进EMD方法在滑坡变形监测中的应用
李胜天 张 军
(江西省地质局地理信息工程大队 江西南昌 330001)
滑坡是斜岩坡沿着贯通的剪切破坏面发生的地质滑移现象,造成滑坡的影响因素较多,如地震、雨水冲刷和地质变形等[1]。滑坡不仅会给人民生命财产安全带来危险,同时也会破坏生态环境的稳定性,因此,准确掌握滑坡的变形状态及趋势具有重要意义。由于诱发滑坡的外界因素的随机性较高,所以滑坡系统通常表现出非常复杂的非线性特征,故针对滑坡变形监测的处理具有较高的难度,尤其是对滑坡变形的准确预测。
在对滑坡进行预测时,首先需要对监测序列进行分解得到平稳序列,对平稳序列进行预测能有效提高预测精度。作为一种具有较强自适应性的信号处理方法,经验模态分解(Empirical Mode Decomposition,EMD)目前已经广泛应用在非线性时间序列的信号分离中,并取得了较好的效果[2-4]。例如,张双成[5]等通过EMD方法提取得到GPS时间序列中两年周期地表垂直形变;贾瑞生等[6]将EMD方法应用于微震信号中噪声的分离,效果显著;王笑蕾等[7]结合EMD方法与WD方法,从GPS时间序列中提取得到半周年、周年的周期震荡。但是, EMD方法在使用过程中存在端点效应,影响了EMD方法在时间序列处理中的精度。本文基于函数延拓原理,提出了一种抑制端点效应的改进EMD方法,并通过仿真试验与实际滑坡监测数据对改进方法的有效性与可靠性进行检验。
1 滑坡监测方法
1.1 EMD方法
EMD方法作为一种对非线性和非平稳性信号具有良好自适应处理性能的信号处理方法,能够将信号分解为若干个不同频段的本征模态函数(Intrinsic Mode Function,IMF)及趋势项。每个IMF分量从原始信号中分解出来都需要满足以下两个条件[8]:
1)任意时刻局部最小值的下包络线与局部最大值的上包络线的平均值为0;
2)整个序列中的过0点与极值点数量相等或者最多差一个。
假设存在一信号x(t),首先,通过三次样条函数插值,得到上包络线u+(t)、下包络线u-(t)和上下包络线均值u1(t),根据原始信号与上下包络线均值计算得到第一个信号分量h1(t)=x(t)-u1(t)。
其次,对第一个信号分量进行IMF分量条件符合检测,若h1(t)符合IMF分量条件,则h1(t)为IMF分量;若不符合IMF分量条件,则使用第一个信号分量代替原始信号继续进行分解,直至得到满足IMF分量的信号分量h1k。用a1(a1=h1k)表示第一个IMF分量。
再次,将a1从原始信号中分离出来,得到剩余信号r1=x(t)-a1。
最后,对r1重复前3个步骤,依次得到第二个、第三个直至最后一个IMF分量,最终得到一个趋势项剩余信号rn,有:
(1)
不同的IMF分量可以反映信号的不同频率成分,所有的IMF分量是从高频到低频依次分布,趋势项剩余信号是原始信号x(t)的单调趋势项。
1.2 抑制了端点效应的改进EMD方法
根据端点附近极大值与极小值处斜率相等的特征,在两端点分别延拓出极值点用于构造上下包络线。端点延拓极值点的流程如下:
1)将起始延拓的极大值点设定为起始端点Z(0),计算起始端点与邻近极大值点间的斜率:
(2)
式中:K1为起始端点与邻近极大值点间的斜率;u(1)为相邻极大值点;u(0)为起点延拓的极大值点,u(0)=Z(0);tmax(1)为相邻极大值点的横坐标;tmax(0)为延拓的极大值点的横坐标。
2)通过起始端点延拓,得到起始端点的极小值点及其横坐标。
V(0)=V(1)-K1·[tmin(1)-tmin(0)]
(3)
式中:V(0)为起始端点延拓的极小值点,V(1)为相邻极小值点,tmin(1)为相邻极小值点的横坐标,tmin(0)为延拓的极小值点的横坐标。
3)假设末端延拓的极小值点为终止端点Z(n),计算终止端点与相邻极值点的斜率。
(4)
式中:K2为终止端点与邻近极小值点间的斜率;V(Nmin-1)为相邻极小值点;V(Nmin)为终止端点延拓的极小值点,V(Nmin)=Z(n);tn(Nmin-1)为相邻极小值点的横坐标;t(Nmin)为延拓的极小值点的横坐标。
4)通过终止端点延拓,得到终止端点的极大值点及其横坐标。
u(Nmax)=u(Nmax-1)-K2·[tmax(Nmax-1)-
tmax(Nmax)]
(5)
式中:u(Nmax)为末端延拓的极大值点,u(Nmax-1)为相邻极大值点;tmax(Nmax-1)为相邻极大值点的横坐标,tmax(Nmax)为末端延拓的极大值点的横坐标。
通过上述流程,在时间序列两端点延拓出极值点,可避免将端点作为极值点,产生端点效应。改进EMD方法实现流程如图1所示。
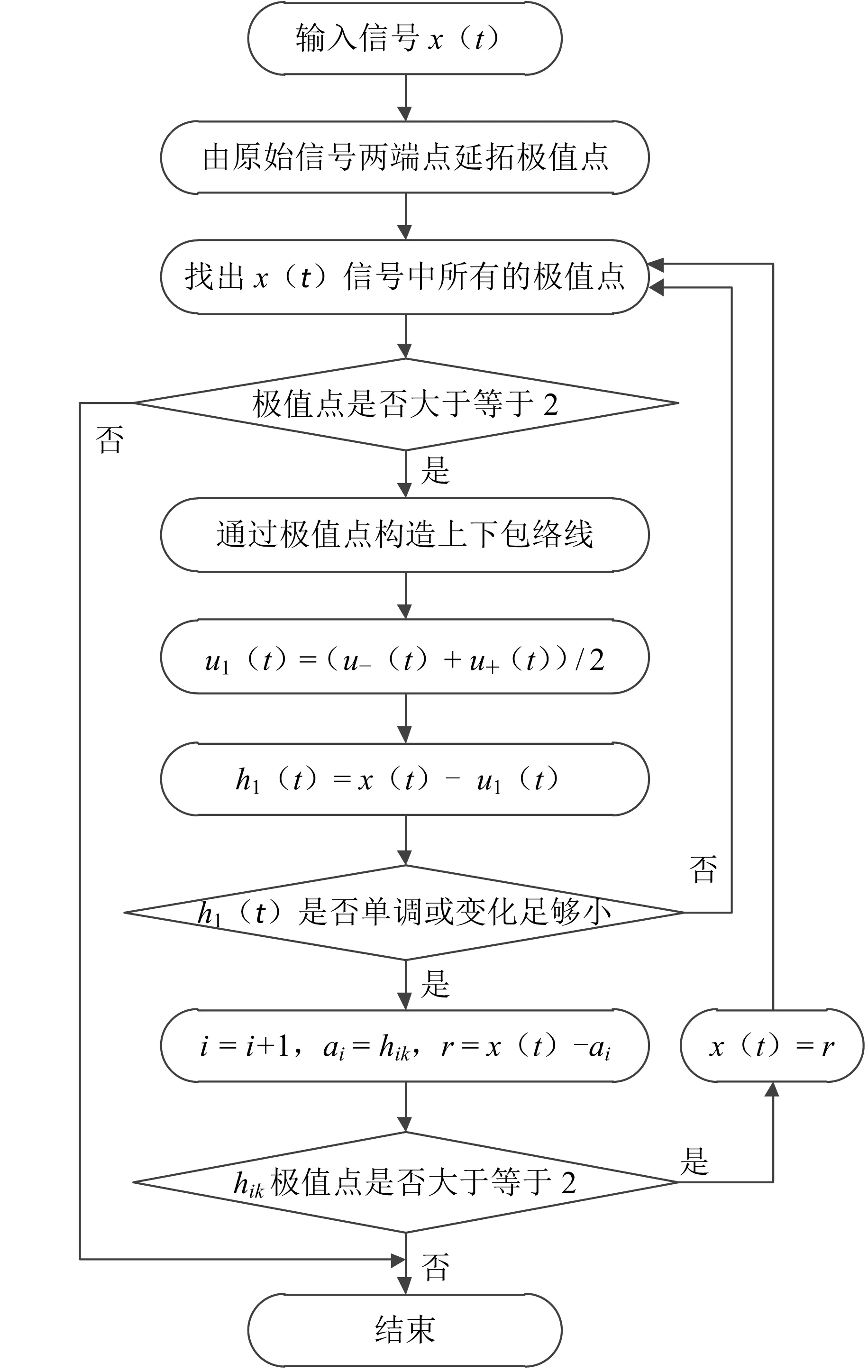
图1 改进EMD方法技术路线
2 仿真试验
为了验证改进EMD方法抑制端点效应的效果,本文通过仿真试验定量分析改进EMD方法与传统EMD方法的差异。
2.1 抑制端点效应评价指标
为了评价不同EMD方法的优劣,本文选取分解误差和相似系数两种定量评价指标来判定不同EMD方法抑制端点效应的效果。
1)分解误差。计算经过EMD方法分解后的各分量IMF与对应的原始信号分量的平均相对误差,以此评价各分量IMF的准确度。分解误差可表示为[10]
(6)
式中:mIMFi为分解误差,xi(k)为第i个原始信号的分量,IMFi(k)为经过EMD方法分解后的对应分量。
从式(6)可以看出,平均相对误差越小,抑制端点效应的效果越好。
2)相似系数。计算经过EMD方法分解后的各IMF分量和对应的原始信号分量的相似系数,以此评估抑制端点效应方法的效果[11]。相似系数ρ可表示为
(7)
式中:cov为协方差,σ为方差,IMFi为经过EMD方法分解后信号的第i个模态分量,xi为对应的原始信号分量。
从式(7)可以看到,相似系数越大,抑制端点效应的效果越好。
2.2 仿真试验分析
测试信号为一非线性仿真信号,采样点数为250个点,采样频率为1 000 Hz。为了更好地比较分解的结果,给出原始信号的组成分量,如图2所示。

图2 原始仿真信号的组成分量
仿真信号经传统EMD方法和改进EMD方法分解得到的结果如图3所示,原始信号通过传统EMD方法与改进EMD方法分解得到各分量的相对分解误差和相似系数见表1。

表1 传统EMD方法与改进EMD方法分解结果对比Tab.1 Contrast of Decomposition Results between Traditional EMD Method and Improved EMD Method指标传统EMD方法IMF1IMF2改进EMD方法IMF1IMF2mIMFi/%0.450.620.190.22ρ0.882 30.884 30.904 20.912 3处理时间/s0.348 30.214 2
由图3可知,传统EMD方法中IMF1、IMF2的两端产生了较为明显的端点效应,幅值也均相应减小,其中IMF2的误差更大,逐渐回向内传播;改进EMD方法有效改善了端点效应。结合表1可以看出,对于给出的仿真信号,改进EMD方法分解得到分量的的分解误差更小,相似系数更大,分解精度较传统EMD方法更高,表现出了更好的分解性能。

图3 传统EMD方法和改进EMD方法分解结果
3 工程应用
为了检验改进EMD方法在实际工程项目中的应用效果,选择某滑坡变形监测中40期沉降监测数据进行验证。本文结合BP神经网络模型,分别使用传统EMD方法和改进EMD方法进行沉降预测。BP神经网络模型是一个不需要对输入与输出关系进行数学描述的模型[9],是通过对输出误差进行逆向传播,不断地优化网络模型中的关键参数,实现模型最优化。
首先,对沉降监测序列分别使用传统EMD方法和改进EMD方法进行分解,使用分解误差与相似系数两个指标对分解结果进行定量评价,结果见表2。

表2 传统EMD方法与改进EMD方法分解结果对比Tab.2 Contrast of Decomposition Results between Traditional EMD Method and Improved EMD Method指标传统EMD方法IMF1IMF2改进EMD方法IMF1IMF2mIMFi/%0.006 40.007 10.003 50.004 4ρ0.878 40.855 60.914 80.925 1
由表2可知,改进EMD方法比传统EMD方法的分解误差更小,相似系数更大,进一步验证了改进EMD方法的分解精度更高。
其次,对分解后的各分量进行BP神经网络模型预测。选择前30期数据作为训练样本,预测后10期累积沉降量。BP神经网络模型中的参数设置至关重要,直接影响模型预测效果,经过重复试验,最终确定BP神经网络模型的输入层、隐含层和输出层分别为5、13、1。
最后,将BP神经网络模型预测各分量值进行重构,得到传统EMD方法和改进EMD方法下的BP神经网络模型,其预测结果如图4和表3所示。

图4 传统EMD方法与改进EMD方法拟合预测结果
由图5可知,基于改进EMD方法的BP神经网络模型的预测精度比基于传统EMD方法的BP神经网络模型的预测精度更高,预测的累积沉降量曲线与实测值更接近。由于改进EMD方法的分解精度更高,在进行信号分解时能剔除更多的噪声,从而避免了噪声对预测结果的影响。
根据表3数据计算均方误差,基于传统EMD方法的BP神经网络模型预测结果的均方误差为±1.03 mm,基于改进EMD方法的BP神经网络模型预测结果的均方误差为±0.70 mm。表明改进EMD方法的BP神经网络模型预测精度更高。
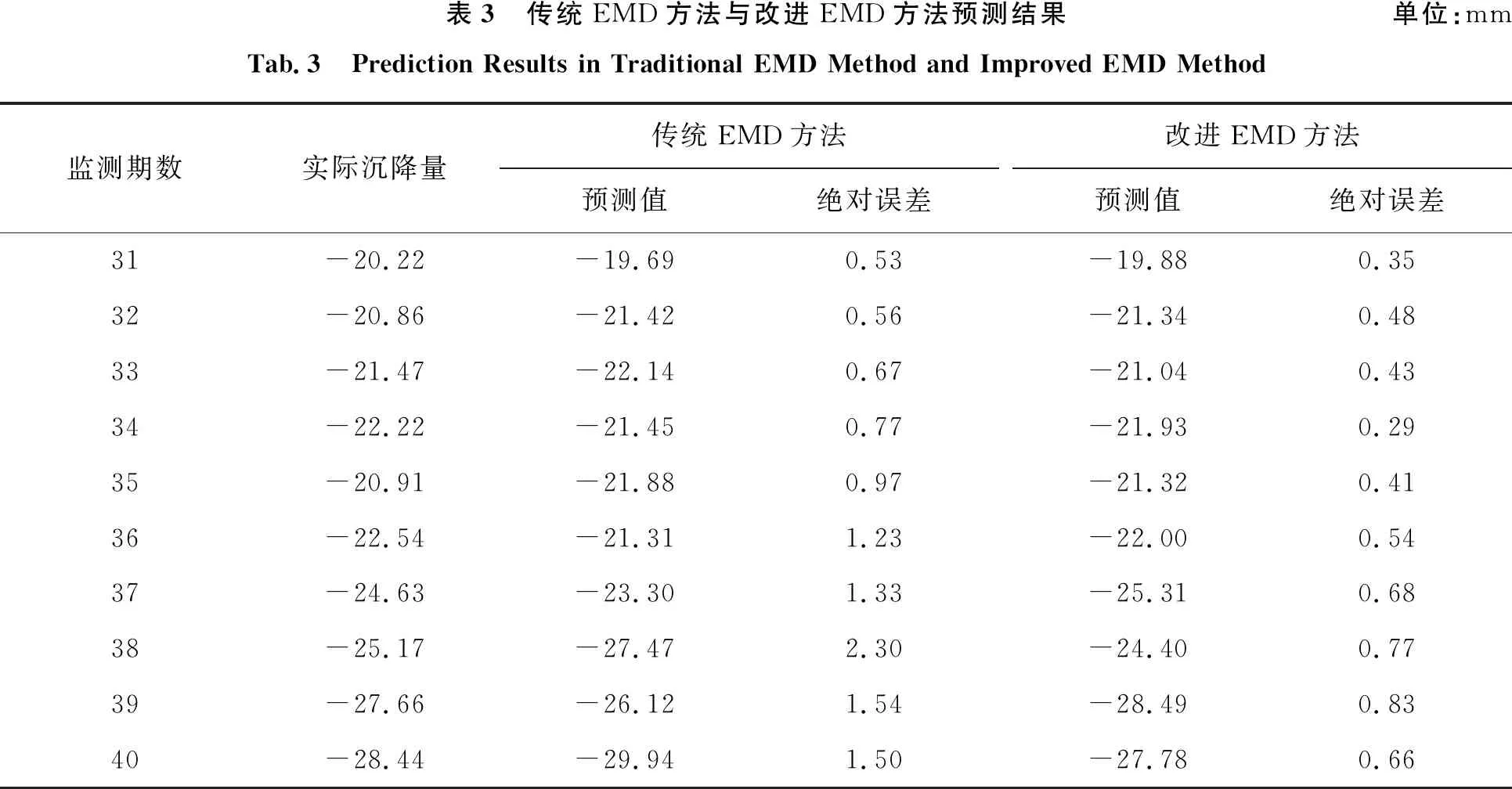
表3 传统EMD方法与改进EMD方法预测结果单位:mmTab.3 Prediction Results in Traditional EMD Method and Improved EMD Method监测期数实际沉降量传统EMD方法预测值绝对误差改进EMD方法预测值绝对误差31-20.22-19.690.53-19.880.3532-20.86-21.420.56-21.340.4833-21.47-22.140.67-21.040.4334-22.22-21.450.77-21.930.2935-20.91-21.880.97-21.320.4136-22.54-21.311.23-22.000.5437-24.63-23.301.33-25.310.6838-25.17-27.472.30-24.400.7739-27.66-26.121.54-28.490.8340-28.44-29.941.50-27.780.66
4 结 语
本文将平行极值延拓理论应用于对传统EMD方法的改进,并通过仿真试验从分解误差与相关系数两个维度对改进EMD方法的端点抑制性能进行评价,采用实测数据结合BP神经网络模型,使用传统EMD方法和改进EMD方法进行沉降预测。
结果表明,改进EMD方法的分解精度更高,改进EMD方法结合BP神经网络模型进行预测的均方误差小于传统EMD方法,表明改进EMD方法在实际应用中有着较高的价值。

