基于三步搜索法的LSSVM在GPS高程拟合中的应用

朱 华

(南京安厦房屋安全鉴定检测事务所有限公司 江苏南京 210029)

GNSS技术在工程测量中被广泛应用，然而GNSS采用的是大地高，与我国规定的正常高之间存在高程异常，可以通过高程拟合来实现两者的转换。

最小二乘支持向量机(LSSVM)是一种数据分类和回归工具[1]，基于结构风险最小化原则，将最小二乘估计引入支持向量机中，采用等式约束代替不等式约束，训练过程转化为求解线性方程组，避开了二次归化问题，求解速度加快，不需要指定逼近精度[2-3]。

LSSVM参数的取值在很大程度上决定了模型的学习和泛化能力，目前还没有切实可行的参数调节方法。

本文采用三步搜索法对LSSVM参数进行优化选择，并用参考文献[3]的GPS观测数据，对适应度函数采用学习样本、测试样本和总样本均方误差的拟合效果进行分析比较。

1 LSSVM机及三步搜索法

1.1 LSSVM

给定M个训练样本的集合{xi，yi}(i=1，2，…，M)，xi∈Rn，yi∈R。根据结构风险最小化原则，回归问题可表示为约束优化问题。

(1)

式中：权矢量w∈Rn，φ(x)是将x从输入空间映射到高维特征空间的函数，误差项ε∈R，C为正则化参数，b为偏差量，s、t、y是约束条件。

引入Lagrange乘子αi，将式(1)转化为无约束目标函数：

(2)

结合式(1)中的约束条件对式(2)进行优化，可得

(3)

式中：α=(α1α2…αM)T，Ω=[φ(x1)φ(x2) …φ(xM)]T，Y=(y1y2…yM)T，I=(1 1 … 1)T。

通过引入满足Mercer条件的核函数K(x，xi)，代替非线性拟合的ΩΩT内积运算，得到最小二乘支持向量机的回归函数：

(4)

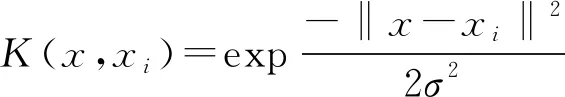
1.2 三步搜索法

LSSVM核函数选择径向基核函数时，正则化参数C和核函数宽度σ的取值在很大程度上决定了模型的学习和泛化能力。

确定C和σ的取值范围，若C和σ的取值点分别有NC和Nσ个，采用完全搜索法则需要计算NC×Nσ次。而相对于完全搜索法，三步搜索法计算简单，性能良好，能有效降低计算次数，缩短建模时间。采用三步搜索法首先需要确定步长。在由C和σ构成的二维平面中，通常设定三步的步长之和为平面边长的一半。三步搜索法的操作步骤如下：

第一步：首先找到中心点及其周围8个点，然后计算每个点的适应值，选择适应值最小的点作为新中心点；

第二步：将步长减小一半，计算新中心点周围8个点的适应值，然后选择适应值最小的点作为下一个新的中心点；

第三步：重复第二步，直至步长小于一个单位。

若学习精度没达到所需要求，则返回第一步继续寻找；若达到精度要求，则作为选择的参数对[5-6]。

2 实例应用

本文采用文献[3]中的GPS观测数据进行建模分析，对拟合后的结果选用内、外符合精度作为评价指标。

(5)

式中：u1、u2为内、外符合精度，v1、v2为训练样本和测试样本高程异常拟合残差，n1、n2为训练样本和测试样本个数。

在进行GPS高程拟合前，为避免所用数据的数值较大对拟合结果产生影响，需要对数据进行预处理[7]。LSSVM参数在寻优时，适应度函数[8]选择学习样本均方误差可能会存在过拟合的情况，使得预测效果不理想。本文采用三步搜索法寻找最优参数组合，适应度函数分别选择学习样本、测试样本和总样本均方误差，并对其拟合效果进行分析比较。

为了计算方便，通过多次试验确定C和σ的取值范围分别为[100，1 500]和[0.5，1.9]，则：

第一步：中心点为(800，1.2)，步长为(400,0.4)，计算中心点及其周围8个点的适应值，选择适应值最小的点作为新的中心点。

第二步：将步长减小一半为(200，0.2)，计算新中心点周围8个点的适应值，选择适应值最小的点作为下一个新的中心点。

第三步：将步长减小为(100，0.1)(步长小于一个单位)，计算新的中心点周围8个点的适应值，适应值最小的点即为最终选择的点。

采用三步搜索法最终获得C和σ的最优组合分别为(1 500，0.5)、(1 500，1.2)和(700，0.9)。

图1是在寻找最优参数时训练样本和测试样本的高程异常拟合残差图，表1是选择的几种适应度函数模型的拟合精度。

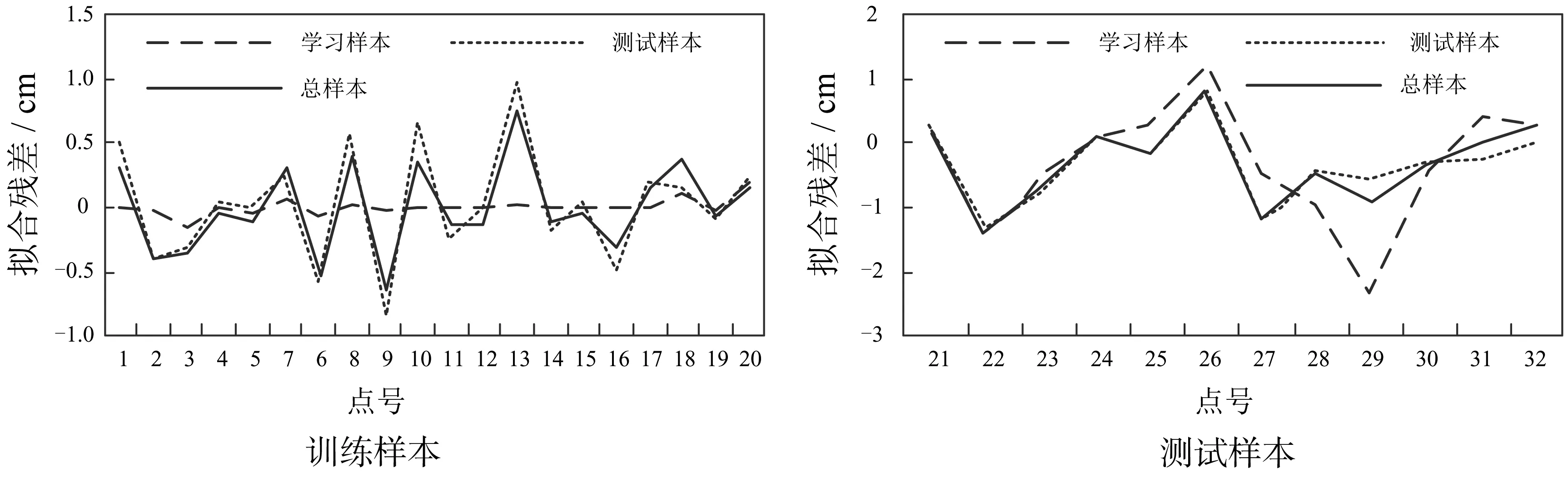
图1 训练样本和测试样本的高程异常拟合残差

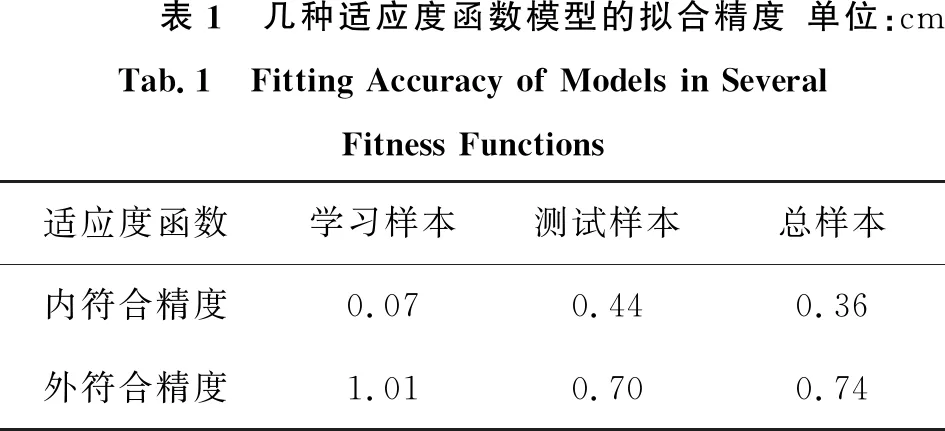
表1 几种适应度函数模型的拟合精度单位:cmTab.1 Fitting Accuracy of Models in Several Fitness Functions 适应度函数学习样本测试样本总样本内符合精度0.070.440.36外符合精度1.010.700.74

从图1和表1可以看出，适应度函数采用学习样本均方误差，训练样本可能存在过拟合的情况，测试样本部分点的高程异常拟合值较大，拟合效果不佳；采用测试样本和总样本均方误差时，训练样本和测试样本的高程异常拟合值都比较稳定、一致，拟合效果要优于采用学习样本均方误差，拟合精度相对更高，能够达到四等水准测量的精度要求，可以满足一般的工程测量的要求。

3 结 语

GNSS高程拟合在工程测量中有着广泛的应用，最小二乘支持向量机在GNSS高程拟合中有着一定的优势。最小二乘支持向量机参数寻优采用三步搜索法，相对于完全搜索，计算简单，能有效降低计算次数，缩短建模时间。通过采用GPS数据对拟合效果进行比较，适应度函数选择测试样本和总样本均方误差的拟合效果要优于选择学习样本均方误差。但是如何对最小二乘支持向量机参数进行优化选择仍需要进一步研究。