基于RBF神经网络组合模型的GNSS高程拟合
李林晓 周鸿芸
(1.广东省测绘技术公司 广东广州 510700;2.广州市黄埔区不动产登记中心 广东广州 510700)
影响工程建设质量的一个关键因素是三维坐标的测量精度。目前,二维平面测量精度可以达到毫米级,因此工程质量符合要求的关键在于高程测量精度。高程系统中主要包括3类,分别为大地高、正高及正常高[1]。我国实际工程中采用的是正常高系统H,而GNSS采用的则是以参考椭球面为基准的大地高系统h。正常高系统H与大地高系统h之间存在差值,即高程异常ζ。对于工程建设项目而言,对正常高H的精度要求不是特别高,使用全球导航卫星系统进行大地高测量具有全天候数据采集等优势。因此,研究将大地高转换为满足工程项目中要求的正常高,即求解高程异常ζ具有重要意义。
目前常用的高程异常ζ拟合方法主要有多面函数法、多项式曲面法及BP神经网络模型等[2]。蒲伦等[3]针对复杂地形,使用蚁群算法寻找多面函数中心,同时为削弱粗差影响,提高高程拟合精度,引入稳健估计的算法;党金涛等[4]使用总体最小二乘进行拟合推估,提高了多项式曲面法的拟合精度;李崇伟等[5]针对BP神经网络模型中隐含层神经元等参数选取,对BP神经网络模型拟合精度的影响进行了研究与分析;高宁等[6]将径向基(Radial Basis Function,RBF)神经网络模型应用于矿区高程拟合中,结果表明,RBF神经网络模型的拟合精度较BP神经网络模型更高,但稳定性有待提高。
上述这些研究中,高程拟合模型均属于单一模型,且分别从模型误差和模型适用范围等方面对模型拟合精度进行讨论。本文在RBF神经网络模型的基础上,提出将改进的自适应权重粒子群算法应用于RBF神经网络模型中关键参数的自动优化选取,以提高RBF神经网络模型的稳定性与拟合精度。最后,使用某测区的实测GNSS数据,将本文改进模型的高程拟合结果与BP神经网络模型、RBF神经网络模型的高程拟合结果进行对比,以验证本文改进模型的精度。
1 神经网络模型
1.1 BP神经网络模型
BP神经网络模型是一种不需要对输入值与输出值进行描述的数学方程[7],其数据处理的主要方式是对输出值与期望输出值之间的误差进行反向传播,以不断调整神经网络中的权值,使得最终输出的结果满足精度要求。BP神经网络模型的算法结构如图1所示。

图1 BP神经网络模型算法结构
对于一样本序列x1,x2,…,xn,首先设置阈值θ及初始权值w1,w2,…,wn,然后基于BP神经网络模型的正向传播,根据参数可计算得到隐含层神经元输入值uj。
(1)
根据激活函数及隐含层输入值,计算得到下一层输入值f(uj)。
(2)
根据计算的每一隐含层的输出值,得到输出层的输出值ζ*就表示第一次正向传播过程的完成。
其次,对输出值的误差δ进行统计:
(3)
式中:ζ*为BP神经网络模型的输出值,ζ为期望输出值。
最后,对误差δ进行判断,若δ超出精度要求,则根据δ对阈值θ及权值w不断优化调整,完成反向传播过程。
总之,BP神经网络模型就是选择正向传播过程参数与反向优化参数,最终得到满足精度要求的输出值,则表明BP神经网络模型训练过程的完成。
1.2 RBF神经网络模型
BP神经网络模型在进行参数优化调整时,使用的是负梯度下降的方法,存在局部极小、收敛速度慢等问题,因而引入一种新的前馈式神经网络——RBF神经网络。RBF神经网络可以对任意非线性函数进行逼近,具有非线性映射能力强、运算速度快等优点,目前已经广泛应用在多个领域[8]。RBF神经网络模型由输入层、径向基函数层及线性输出层组成,其算法结构如图2所示。

图2 RBF神经网络模型算法结构
RBF神经网络模型的输入层共包含N个神经元节点,RBF层神经元节点数为R,输出层有M个神经元节点数。将输出层神经元i与RBF层神经元j的连接权定为Wji,那么权向量为
Wj=(Wj1,Wj2,…,WjN),j=1,2,…,R
(4)
将输入层神经元与RBF层神经元的连接权阵定为Wl,表示为
Wl=(W1W2…WR)T
(5)
利用RBF神经网络模型进行GNSS高程拟合包括两个阶段:一是采用无导数训练方式对RBF层的权值W1和偏差b1进行训练;二是采用有导数训练方式对输出层的权值W2和偏差b2进行训练。
2 改进粒子群优化算法
2.1 粒子群优化算法
粒子群优化算法(Particle Swarm Optimization,PSO)是通过模拟鸟群觅食行为而发展起来的随机搜索算法,通常被认为是群集智能的一种[9]。在一个n维空间中,假设参与问题求解的粒子数为m,其中,第i个粒子的位置表示为Xi(xi1,xi2,…,xin),速度表示为Vi(vi1,vi2,…,vin),对位置与速度进行更新,可表示为
Xi(d+1)=Xid+r×Vid
(6)
Vi(d+1)=w×Vid+c1r1(Pid-Xid)+c2r2(Pgd-Xid)
(7)
式中:Xid、Vid分别为第d次迭代时的位置与速度,c1、c2为算法学习因子,Pgd为粒子群最优位置,w为惯性权重,r、r1、r2是介于0至1之间的随机数。
2.2 自适应权重粒子群算法
自适应权重粒子群优化算法中,当粒子适应度大于平均适应度时,惯性权重更新方式为
(8)
式中:fmin为粒子群最小适应度,favg为粒子群平均适应度,w为惯性权重。
2.3 改进的自适应权重粒子群优化算法
黄洋等[10]通过重新定义惯性权重更新方式,提出了一种基于S型函数的自适应粒子群优化算法,其惯性权重更新方式为
(9)
式中:a、b为系数,a取3.4,b取0.07,t为当前迭代次数。
对应于粒子适应度与平均适应度的不同关系,分别使用式(8)与式(9)进行权重更新,位置更新方式为
(10)
2.4 仿真试验
使用函数f=20+x2+y2-10[cos(2πx)+cos(2πy)]进行10次仿真试验,对本文提出的改进粒子群优化算法的性能进行检验。该函数在(0,0)点具有最小值0,寻优结果统计如表1所示(表中FV为函数值,X、Y为最优粒子平面位置坐标)。

表1 3种粒子群算法的寻优结果统计 单位:mTab.1 Statistics of Optimization Results in Three Ways of PSO粒子群算法XYFV自适应权重粒子群算法XYFV改进粒子群优化算法XYFV20.54×10-3-16.64×10-3227.02×10-3-5.40×10-11-1.10×10-90-7.10×10-101.66×10-100864.82×10-3-807.52×10-33 078.08×10-32.57×10-9883.85×10-3883.85×10-3-2.80×10-92.45×10-100881.60×10-3877.58×10-31 887.60×10-3-1.50×10-92.09×10-902.80×10-9-4.20×10-100858.51×10-330.17×10-31 330.82×10-32.70×10-99.27×10-1001.02×10-92.33×10-901 002.28×10-3-841.01×10-32 253.53×10-33.35×10-10-1.70×10-901.81×10-9-8.70×10-1101 012.03×10-366.22×10-32 203.50×10-32.08×10-9-1.60×10-90-2.40×10-9-2.00×10-100-20.07×10-3-0.76×10-3180.06×10-31.02×10-106.21×10-1001.82×10-9-1.10×10-90-12.74×10-3-73.25×10-31 306.32×10-31.30×10-9883.85×10-3883.85×10-3-4.30×10-10-1.30×10-90-7.57×10-3-21.47×10-3211.04×10-3883.85×10-3-3.40×10-9883.85×10-32.55×10-91.12×10-90-27.03×10-3-867.18×10-31 226.01×10-3-883.85×10-32.47×10-9883.85×10-3-1.30×10-9-1.30×10-90
从表1可知,相比于另外两种粒子群寻优算法,本文提出的改进粒子群寻优算法得到的结果精度最高。通过计算,相比于自适应权重粒子群算法,本文提出的改进粒子群算法的精度提高了24%。
3 改进的RBF神经网络高程拟合
RBF神经网络进行高程拟合的结果精度及稳定性受相关参数因子决定,并且高程拟合时需要提前设置参数因子。参数因子最优值是根据试验数据进行设置的。针对特定的数据设置的参数因子可能是最优值,但是拟合数据发生变化,参数因子最优值也会发生改变。本文使用RBF神经网络进行高程拟合时,引入改进的粒子群优化算法,目的是充分利用该算法良好的寻优能力。将改进的粒子群优化算法与MATLAB中newerbe函数构建的RBF神经网络模型结合,以发挥该算法在RBF神经网络模型SPREAD值与隐含层节点数自动化寻优中的作用,提高网络模型拟合的稳定性与精度。将改进的粒子群优化算法与RBF神经网络模型结合,组合生成新的改进RBF神经网络组合模型算法,并将该算法应用于GNSS高程拟合中,主要流程如下:
1)为了避免数据过大对拟合结果造成影响,使用MATLAB中的mapminmax函数对数据进行归一化处理;
2)在RBF神经网络模型中输入训练数据,使用改进的粒子群优化算法确定RBF神经网络中的关键参数SPREAD值与隐含层节点数据,得到完整的神经网络模型;
3)将测试数据加入模型中,计算得到拟合值,使用拟合残差和外符合精度两种评价指标对改进的RBF神经网络模型的高程拟合结果进行评估。
4 试验与结果分析
4.1 试验数据

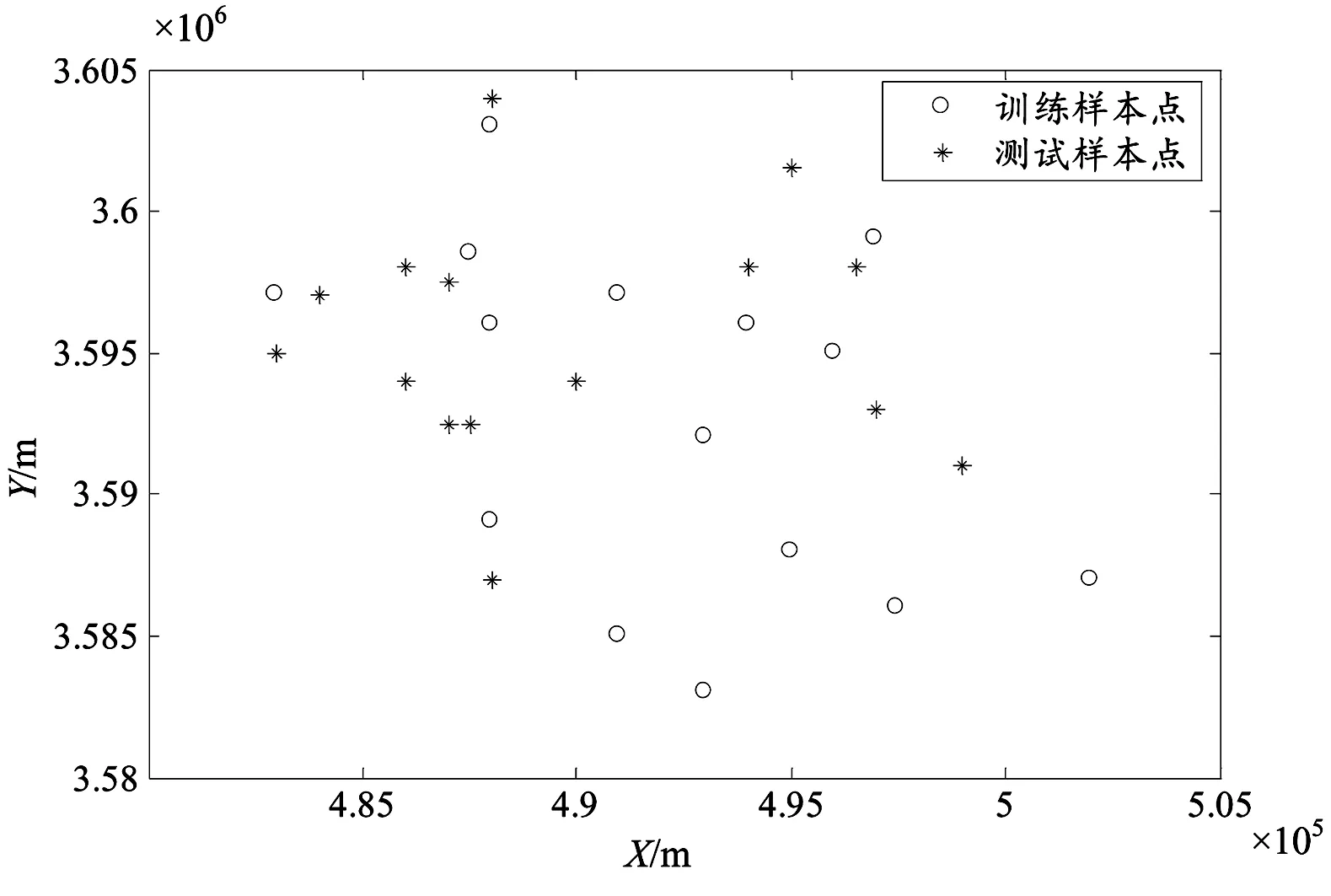
图3 测区四等水准联测点分布
为了使数据计算更方便并减少计算精度损失,试验开始前对四等水准联测点的平面坐标进行了中心化处理。另外,在使用BP神经网络和RBF神经网络模型进行高程拟合时,为了使输入数据在激活函数的作用区间内,对输入数据进行归一化处理,归一化至[-1,1]内,完成样本训练与高程拟合后再对输出数据进行反归一化处理。
4.2 评价指标
为了对高程拟合模型的拟合结果进行判断,统计模型高程拟合结果的拟合残差和外符合精度[11]。
(11)
(12)

4.3 结果分析
使用BP神经网络模型、RBF神经网络模型与改进RBF神经网络组合模型对测区水准点进行高程拟合,其拟合残差与外符合精度统计如表2所示,拟合残差比较如图4所示。

图4 3种模型高程拟合残差

表2 3种拟合模型的拟合结果统计单位:mmTab.2 Statistics of Fitting Results in Three Fitting Models模 型BP神经网络模型RBF神经网络模型改进RBF神经网络组合模型菪ζmin1.690.980.11菪ζmax11.9810.225.22菪ζ均值7.424.952.69M8.636.013.14
由表2可知,相比于BP神经网络模型,RBF神经网络模型与改进RBF神经网络组合模型的高程拟合结果都有一定程度的提高,其中外符合精度分别提高了30.36%与63.62%,拟合残差也都有不同程度的降低。由于基于BP神经网络模型的高程拟合是一种非线性映射,具有一定程度的随机性,而RBF神经网络模型能更好地对高程异常分布的真实情况进行模拟。相比于RBF神经网络模型,改进RBF神经网络组合模型能对网络中的参数进行自适应确定,高程拟合的稳定性与精度都更高,外符合精度相比RBF神经网络模型提高了47.76%。从图4可以看到,改进RBF神经网络组合模型相比于另外两种模型,其拟合残差的变化幅度更小,更接近于0,拟合效果最佳。
4.4 算法适应性分析
本试验所使用的高程拟合水准点的区域较为平坦,而在实际的工程项目中地形通常都较为复杂,并且高程异常拟合与重力场精度、地形及拟合点分布都具有一定的关系。为了检验本文算法对不同复杂地形是否具有普适性,选择一复杂地形的数据进行相同的高程拟合试验,其中,水准点联测路线长度约为112 km,其闭合差限差为±211.66 mm。通过计算试验数据闭合差为-41 mm。同样选择30个水准点,同样将前15个水准点高程数据作为训练数据,后15个水准点数据作为拟合数据。3种模型计算得到的拟合残差与外符合精度如表3所示。
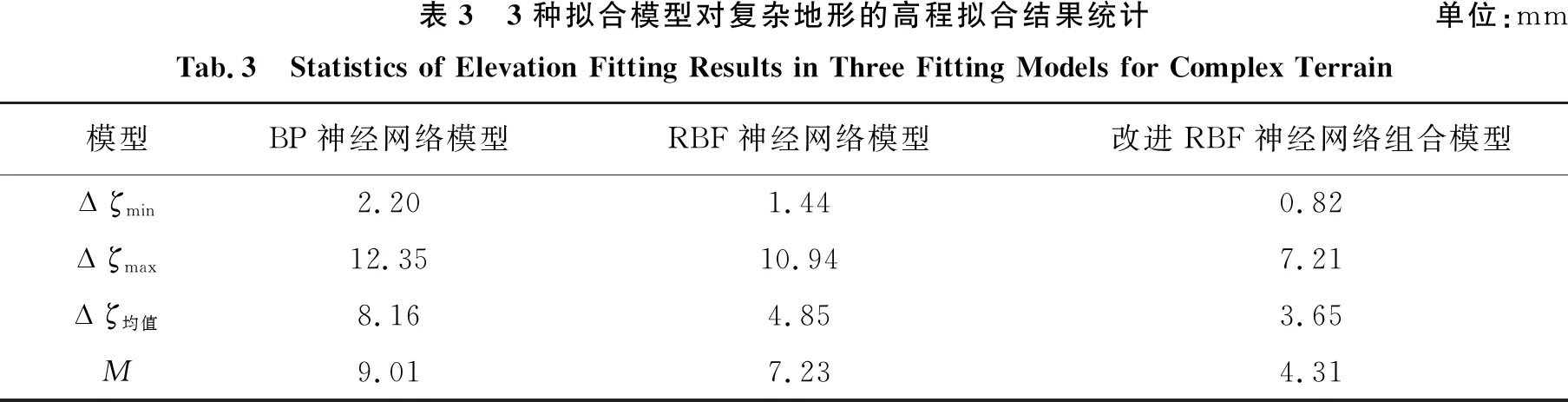
表3 3种拟合模型对复杂地形的高程拟合结果统计单位:mmTab.3 Statistics of Elevation Fitting Results in Three Fitting Models for Complex Terrain模型BP神经网络模型RBF神经网络模型改进RBF神经网络组合模型菪ζmin2.201.440.82菪ζmax12.3510.947.21菪ζ均值8.164.853.65M9.017.234.31
由表3可知,对于复杂区域的高程拟合,相比于BP神经网络模型,RBF神经网络模型与改进RBF神经网络组合模型的高程拟合结果同样都有一定程度的提高,其中外符合精度分别提高了19.76%与52.16%,拟合残差也都有不同程度的降低;相比RBF神经网络模型,改进RBF神经网络组合模型同样能对网络中的参数进行自适应确定,提高了高程拟合计算的稳定性与精度,外符合精度提高了40.39%。
复杂区域水准点高程数据波动较大,随着高程数据波动性增加,3种拟合方法的拟合残差相比平坦区域都有不同程度的增大,外符合精度也都有不同程度的降低;但相比BP神经网络模型和RBF神经网络模型,改进RBF神经网络组合模型的性能下降更小。因此,对于复杂地形的GNSS高程拟合问题,改进RBF神经网络组合模型仍然能得到较好的拟合结果,说明本文算法对不同复杂地形具有普适性。
5 结 语
本文在RBF神经网络模型基础上,引入改进的粒子群算法,对RBF神经网络模型中的隐含层节点数和SPREAD值关键参数进行优化确定。同时还使用不同地形数据对BP神经网络模型、RBF神经网络模型和改进后的RBF神经网络模型进行试验,采用拟合残差与外符合精度对3种模型的GNSS高程拟合结果进行精度评价。结果表明,不管是在地势平坦区域还是复杂区域,改进RBF神经网络模型的拟合精度均比另外两种模型的拟合精度都高,更适用于实际工程场景的应用。

