环境减灾二号A/B卫星高光谱数据反演与质量提升

冯向朋 陈铁桥,2 张耿 王爽 刘学斌

(1 中国科学院西安光学精密机械研究所，西安 710119)(2 中国科学院大学，北京 100049)

环境减灾二号A/B卫星高光谱成像仪是面向“十二五”减灾与环境应用需求，研制的一套星载宽覆盖、高分辨率高光谱成像仪民用载荷。其接替超期服役12年的环境减灾一号A卫星超光谱成像仪，通过双星同轨组网，在全球目标区获取高光谱遥感图像数据，用于支持我国环境监测、防灾减灾等业务工作，同时为国土资源、水利、农业、林业、地震等多个领域提供卫星数据资源支撑和业务化应用服务。

面向上述领域应用研究，为定量分析提供可靠的数据来源，需要对高光谱遥感图像数据进行相对辐射校正，实现数据质量提升，使得最终生成的数据具备良好的空间信噪比和光谱准确度。相对辐射校正，尤其是遥感数据的相对辐射校正，都是以校正传感器响应度差异为手段来达到消除条带效应和提高数据辐射质量的目的[1]。传统的高光谱遥感图像数据校正，主要分为实验室定标法和在轨统计法2种。实验室定标法采用均匀光源完成对光学系统的不一致标定；在轨统计法基于大量在轨数据统计结果与规律，完成相对辐射校正。

环境减灾二号A/B卫星高光谱成像仪采用大孔径静态干涉高光谱成像技术，使用时空联合调制的方式，直接获取到的数据为不同地物不同光程差下的原始数据。如果使用传统的实验室定标法，均匀光源经过其光学系统后，被探测器捕获的是带有干涉条纹的数据，不能直接生成相对辐射定标系数。而且，其数据产品并不是传感器输出的原始干涉数据，是经过干涉数据反演得到的光谱数据。因此，其条带噪声的去除不仅依赖于对传感器获取数据进行响应不一致性校正，还需要校正经过复杂数学计算和能量分离之后光谱数据的不一致性，这样才能为高光谱遥感图像数据定量分析提供可靠的数据来源。复杂计算和能量分离带来的不一致性，不能使用实验室定标法完成，只能使用在轨统计法进行。但是，如果对浮点型数据进行诸如直方图统计等在轨数据分析，现有计算机是不可能完成的。为了提升环境减灾二号A/B卫星高光谱数据质量，本文综合使用实验室定标法和在轨统计法，对干涉数据和复原后光谱数据进行不一致性校正，从而有效地去除了图像条带，并保持了良好的光谱准确度。

1 高光谱数据反演

1.1 高光谱成像仪

环境减灾二号A/B卫星高光谱成像仪基于大孔径静态干涉光谱成像技术原理，主要包括摆镜、干涉仪、傅氏镜和探测器[2]。其基本组成如图1所示。

图1 高光谱成像仪基本组成Fig.1 Basic component of hyperspectral imager

高光谱成像仪通过时空联合调制的方式，在同一时刻获得全部目标点各自不同光程差位置上的干涉信息，再利用卫星的移动和时间维的采样共同获取完整的干涉信息[3]。其具体过程如图2所示。

图2 高光谱成像仪时空联合调制获取干涉信息Fig.2 Interferometric information obtained from hyperspectral imager by combined space-time modulation

在图2中，第1帧图像包含了t1时刻第1行地物探测器第1个光程差位置上的干涉信息、第2行地物探测器第2个光程差位置上的干涉信息，一直到第m行地物探测器第m个光程差位置上的干涉信息。其中：m为探测器干涉方向像元数目，也就是探测器所有光程差位置的个数。以此类推，第i帧(i=1，2，3，4，…)图像包含了ti时刻第i行地物探测器第1个光程差位置上的干涉信息、第i+1行地物探测器第2个光程差位置上的干涉信息，一直到第i+m-1行地物探测器第m个光程差位置上的干涉信息。本文称这种数据为大孔径静态干涉光谱成像(LASIS)数据。

1.2 高光谱数据反演

高光谱数据的反演过程实际上是目标图谱数据立方体的重构过程，过程如图3所示[4]。对于理想干涉图，仅需要进行实线框中描述的点干涉图提取和傅立叶变换就可以反演出高光谱数据。虚线框所代表的流程是在数据并非理想时的预处理和修正过程。

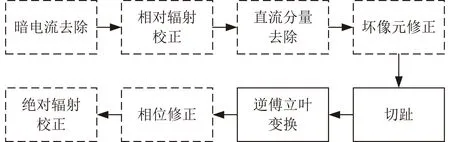
图3 高光谱数据反演一般过程Fig.3 General process of hyperspectral data recovering

由高光谱成像原理可知，要获取同一地物所有光程差下的干涉数据，需要将原始的LASIS数据进行抽取，即要获取第i行地物的完整干涉数据，就必须抽取第i帧数据的第1个光程差位置、第i+1帧数据的第2个光程差位置，一直到第i+m+1行的第m个光程差位置，就可得到1行地物完整的干涉数据，具体如图4[5]所示。

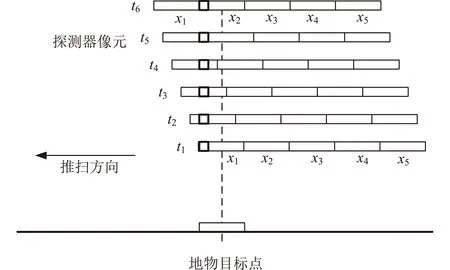
图4 地物目标点完整干涉信息获取方法Fig.4 Acquisition method of integral interference information of ground object target point

高光谱成像仪基本原理建立在光谱与干涉信息之间具有傅立叶变换关系的基础上，仪器通过对干涉信息的采集与变换间接获取光谱信息。假设某一点干涉数据为I(x)，其中，x为沿飞行方向某列探测单元的位置；其复原后点光谱为B(v)={v1,v2,…,vr}，其中，v1为起始波长，vr表示终止波长。I(x)和B(v)相互之间的变换关系可以通过式(1)和式(2)来表示,其中，d为干涉仪剪切量，f为傅氏镜的焦距。

某列探测单元位置x处的干涉强度可表示为[6]

(1)

提取出某一地物目标点的完整干涉图后，经过傅立叶逆变换可以得到该目标点复原后点光谱[6]为

(2)

式中：L为最大光程差。

在干涉仪出现伊始，高光谱数据反演只是通过如式(2)所示简单的傅立叶变换实现[7]。随着干涉光谱技术的发展，相关的数据处理技术不断出现，使得高光谱数据处理的精度不断提高，数据处理流程也不断完善。与高光谱数据处理技术相关的各种误差修正方法及数据处理方法相继被提出，从不同的角度提高了数据处理的精度，完善了高光谱数据处理技术，逐步形成一套通用的光谱数据处理流程(如图3所示)。其计算复杂度高，算法参数多样，可适应不同场景与应用下的光谱复原需求。

2 数据质量提升

在高光谱数据反演过程中，暗电流去除、直流分量去除、坏像元修正、切趾、相位修正、绝对辐射校正环节都有较为固定的方法。例如：切趾过程中较为常用的三角窗、海明窗、海宁窗、Blackman、Norton-Beer等切趾函数[8-10]；相位修正过程中经典的Forman法[11]和Mertz法[12]；去直流分量过程中的差分法[13]、拟合法[14]。

相对辐射校正作为校正探测器响应不一致性、消除条带噪声的直接手段，在干涉数据复原过程中有着重要的作用。但是，由于干涉仪的存在，传统的干涉数据相对辐射校正多采用实验室定标法，去掉前置光学系统(摆镜、干涉仪、傅氏镜)，直接获取探测器不一致性校正系数。这种方式忽略了摆镜每点的反射率不一致性、干涉仪半透半反性能问题和傅氏镜干涉效率问题。

为了提升复原后高光谱数据质量，本文对干涉数据和复原后高光谱数据进行不一致性校正，即利用实验室定标法和统计方式对在轨原始干涉数据直接进行不一致性校正，从而提升复原后高光谱图像的空间一致性。复原后高光谱数据不一致性校正，是对复原后各个谱段数据进行直方图统计，然后进行直方图匹配，得到直方图查找表进行校正。

2.1 干涉数据不一致性校正

干涉数据校正联合使用实验室定标法和在轨统计法进行校正。探测器响应不一致性校正系数通过实验室定标的方式获得：去掉前置光学系统，仅留下探测器对太阳模拟器不同亮度、不同增益数据进行采集，然后计算得到探测器响应不一致性定标系数C1。光学系统的不一致性通过在轨统计法获得，即：统计不同时相下数据，然后通过计算得到每个光程差的相对辐射校正系数C2。具体计算方法如下。

获取多轨原始干涉数据，累加之后求平均值，得到平均干涉数据，如式(3)所示。

(3)

式中：IAVG(p,q)为第p个光程差第q行的平均值；Ia(p,q)为第a帧数据第p个光程差第q行的值；N为干涉数据帧数。

每个光程差下的累计平均值为

(4)

式中：IAVG(p)为第p个光程差下的累计平均值；W为干涉数据帧的列数。

以单行光程差平均值除以行积累平均值，得到相对辐射校正系数C2。其中，C2(p,q)为相对辐射校正中第p个光程差第q列的系数。

(5)

将探测器不一致性校正系数和光学系统不一致性系数合并，得到干涉数据相对辐射校正系数C。

C(p,q)=C1(p,q)C2(p,q)

(6)

式中：C(p,q)为第p个光程差第q列的系数。

2.2 复原后高光谱数据不一致性校正

统计误差及切趾、相位修正、逆傅立叶变换等处理过程中产生的计算误差，导致干涉数据相对辐射校正之后复原数据依然存在条带。而且，这些复杂计算过程产生的不一致性难以通过单一的线性关系进行校正。因此，本文通过直方图匹配的统计学方法[15]对复原后光谱数据进行校正。具体步骤如下。

光谱复原后，因经过复杂计算，数据为浮点FMax，将所有谱段的数据都正整数化到[1,Z]区间，对区间进行直方图统计。归一化过程为

(7)

式中：Dorg(k,l)为正整数化的第k个谱段第l行值；Dfloat(k,l)为复原后第k个谱段第l行原始浮点值；round表示临近取整函数。

统计各个谱段灰度分布直方图概率密度，见式(8)。

PDNorg(k,l)=nDNorg(k,l)/M(k,l)

(8)

式中：PDNorg(k,l)为正整数化后第k个谱段第l行数值的概率密度；nDNorg(k,l)为正整数化后第k个谱段第l行数值在当前样本中的个数；M(k,l)为第k个谱段第l行所有数据在当前统计样本中的总数。

找到能量响应最高的谱段，对概率密度分布函数进行95%的截断，去掉概率分布的拖尾部分，取截断之后的最大值。截断之后的灰度值分布个数如图5所示。

图5 95%截断后能量响应最高谱段的灰度值分布Fig.5 Digital number distribution of 95% truncated for the highest energy response spectral band

假设此时所有谱段中最大值不超过Zsta(图5中最大值不超过2000)，那么要重新将复原后浮点型数据正整数化到[1,Z]区间内，即

(9)

对再次正整数化数据进行直方图统计，获取各谱段灰度分布直方图的概率密度函数为

PD(k,l)=nD(k,l)/R

(10)

式中：PD(k,l)为第k个谱段第l行地物灰度值为D的概率密度函数；nD(k,l)为第k个谱段第l行地物灰度值为D的个数；R为统计地物的行数。

求取各像元的累计直方图的概率密度函数为

(11)

式中：SD(k,l)为灰度值从1到D在第k个谱段第l行的累计直方图。

分别对各谱段的累计直方图进行平均计算，得到不同谱段下的平均累计直方图，见式(12)。

(12)

式中：SD(k)为谱段k从灰度值1到D的累计直方图概率密度函数。

分别对各谱段各行的累计直方图和对应谱段的平均累计直方图进行匹配计算，找出各谱段各行累计直方图和对应谱段平均累计直方图的灰度映射关系，见式(13)。

D(k,l)=gSg(k)≤SD(k,l)≤Sg+1(k)

(13)

式中：Sg(k)为谱段k在灰度值为g时的平均累计直方图概率密度函数。

式(13)表示直方图匹配关系，即：当Sg(k)≤SD(k,l)≤Sg+1(k)时，D(k,l)的值匹配为g。

根据式(13)建立灰度值查找表，在上述统计过程中，本文选取了大量的非饱和干涉数据进行反演和计算，包括裸地、植被、水体、山地、雪地、建筑物等。查找表建立完成后，进行校正。首先使用式(9)进行正整数化，然后对照直方图查找表进行灰度值映射。如果被查找灰度值不在[1，Z]区间，将其设置为Z。

3 试验结果及分析

3.1 干涉数据校正结果

进行干涉数据校正之后，直观结果如图6所示，干涉数据列方向条带与分块现象消除明显。

图6 干涉数据相对辐射校正前后对比Fig.6 Comparison of interference data before and after radiometric correction

3.2 高光谱数据校正结果

如图7所示，高光谱数据相对辐射校正后，其数据质量大大提升；而且，条带噪声得到了有效的去除，保持了很好的光谱准确度。

直方图匹配校正不是基于线性关系的校正，可能会对光谱准确度产生一定的影响。因此，本文使用敦煌定标场和高亮地区实测数据进行分析。分析结果表明：直方图匹配不会对光谱曲线准确度造成过大影响。

光谱曲线准确度计算公式为

(14)

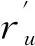
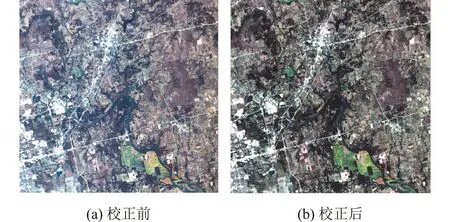
图7 光谱数据相对辐射校正前后图像质量对比Fig.7 Image quality comparison of spectral data before and after radiometric correction

选取敦煌定标场定标区域对光谱准确度进行测试，将L1A级高光谱数据进行绝对辐射校正，得到入瞳辐亮度数据，将定标区域实测图像处理质量标准数据反算到入瞳辐亮度，对比2组数据进行计算，得到光谱曲线准确度。测试区域如图8所示，选取的图像区域如图8中红色矩形框所示，其中，可见光近红外(VNIR)通道数据取10×10像元，短波红外(SWIR)通道数据取5×5像元(红外去除水汽吸收谱段)。环境减灾二号A/B卫星敦煌定标场定标数据光谱准确度曲线如图9和图10所示。从图9和图10可以看出：环境减灾二号A/B卫星的高光谱成像数据光谱准确度已经分别达到97%以上和92%以上。

图8 敦煌定标场Fig.8 Dunhuang calibration field

图9 环境减灾二号A卫星高光谱数据与实测数据对比Fig.9 Comparison between HJ-2A satellite hyperspectral data and measured data

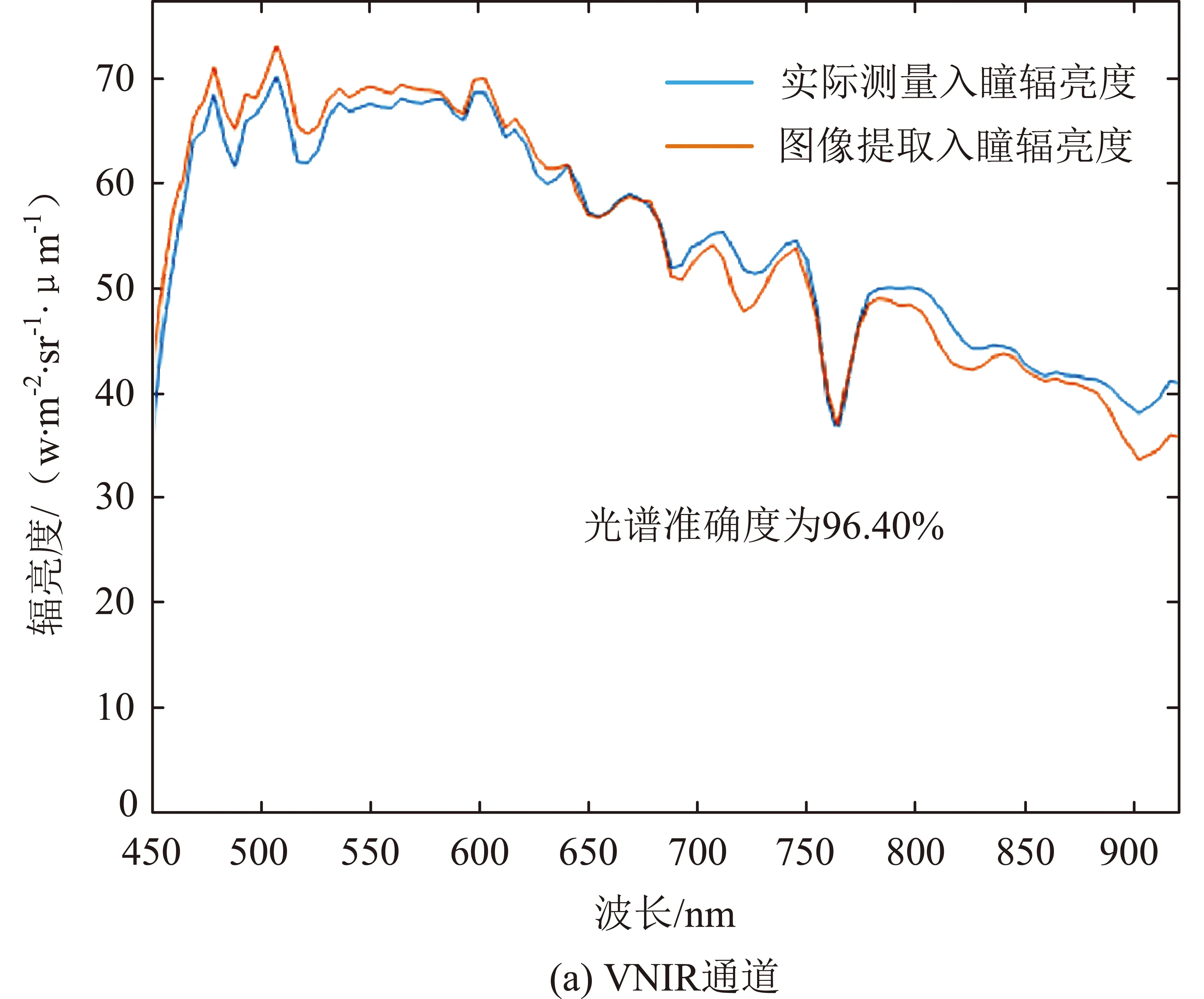
图10 环境减灾二号B卫星高光谱数据与实测数据对比Fig.10 Comparison between HJ-2B satellite hyperspectral data and measured data

选取敦煌定标场北部高亮区域(见图11)不同时相高光谱数据，进行绝对辐射校正得到入瞳辐亮度数据，与实际测量数据进行对比。环境减灾二号A/B卫星光谱准确度结果如图12和图13所示，与实际测量数据的光谱相似度分别达到了93.72%和94.56%。

图11 高亮区域Fig.11 Highlighted region

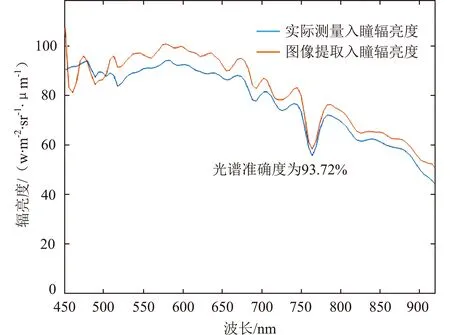
图12 环境减灾二号A卫星VNIR通道高光谱数据与实测数据对比Fig.12 Comparison between HJ-2A satellite VNIR channel hyperspectral data and measured data

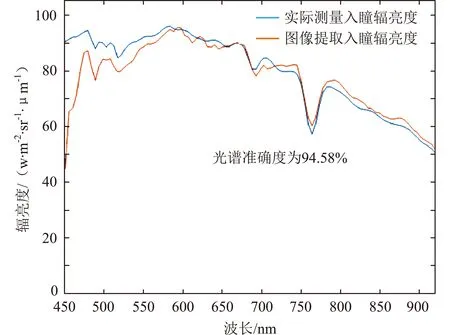
图13 环境减灾二号B卫星VNIR通道高光谱数据与实测数据对比Fig.13 Comparison between HJ-2B satellite VNIR channel hyperspectral data and measured data

表1为上述试验数据的统计结果。其中：VNIR通道数据光谱准确度最低为93.72%，最高可达到97.26%；SWIR通道数据最低为92.06%，最高可达到98.38%。

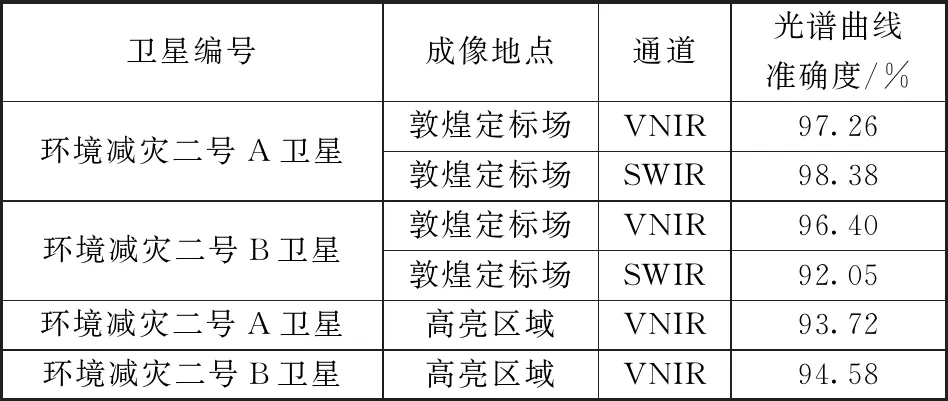
表1 光谱曲线准确度分析结果(绝对光谱准确度)Table 1 Results of spectral curve accuracy analysis (absolute spectral accuracy)

4 结束语

干涉光谱成像数据条带噪声的去除是一个系统性问题，不能仅仅依靠单一的相对辐射校正手段，需要综合使用实验室定标法和在轨数据统计法。本文所述数据质量提升方法，通过降低原始干涉数据响应不一致性噪声和反演后光谱数据中的响应不一致性噪声和计算噪声，具备良好的相对辐射校正效果，并保持了92%以上光谱准确度。在轨数据特征统计过程中，仅仅剔除了少量无效数据(云、饱和数据等)生成干涉数据相对辐射校正系数与复原后光谱数据直方图查找表，有效地解决了载荷光学系统星地环境不一致带来的差异性。综合使用不同的相对辐射校正方法，将原始干涉数据、实验室定标系数校正后干涉数据、干涉数据在轨状态，反演后光谱数据在轨统计结果有机结合，实现更好的干涉光谱成像数据质量提升效果。环境减灾二号A/B卫星高光谱数据质量方法，给出了从机理上校正不同光程差干涉数据的理论，利用直方图统计法和归一化方法将反演后浮点数量化到整数范围，并切除拖尾，使得基于复杂校正原理的反演后浮点高光谱数据校正成为可能。为了完善本文所述复原后相对辐射校正机理，进一步提升光谱准确度，后续将改进复原后直方图匹配方法为线性修正模式。