变系数模型的稳健变量选择与结构识别

聂黎雯

(重庆师范大学 数学科学学院，重庆 401331)

0 引言

变系数模型(Varying Coefficient Models，简称“VCM”)是Hastie和Tibshirani在1993年提出来的一类半参数模型，一般形式为

Y=XTβ(U)+ε，

(1)

其中：Y∈R为模型中的响应变量；X=(X1,…,Xp)T∈RP是p维解释变量；U为指标变量；β(·)=(β1(·),…,βp(·))T是模型中p×1维的函数向量；ε为模型误差.

目前，众多学者对该模型的变量选择和结构识别进行了研究.Lv[1]基于双重SCAD惩罚函数和秩回归，提出了能同时解决参数估计和结构识别的方法.Ma等[2]基于核密度估计与SCAD惩罚函数解决了该模型的统一变量选择问题.Tang等[3]基于自适应LASSO惩罚和两步迭代程序实现了变量选择和结构识别.Zhao[4]基于分位数估计以及核函数实现了变系数模型的统一变量选择.虽然后面两篇文章能同时解决变量选择和结构识别，但是基于最小二乘法和分位数回归.最小二乘法不是稳健估计，分位数回归会因分位数点不同导致结果不同.Zou等[5]首次提出了综合各个分位数点的复合分位数回归(CQR).在异方差的情况下，Yang等[6]考虑了该模型基于复合分位数回归的稳健变量选择.Guo等[7]基于加权复合分位数估计与SCAD惩罚函数实现了该模型的变量选择.Matthew Pietrosanu等[8]讨论了变系数模型的分位数回归和复合分位数回归与组Lasso相结合的变量选择问题.但上述研究没有考虑常系数与变系数的区分.因此，本文基于复合分位数的稳健性与有效性，结合SCAD惩罚函数和B样条基函数近似提出了一种新的双惩罚稳健估计程序，它能够同时进行变量选择和结构识别，而且所得估计具有更好的稳健性和有效性.

1 模型的建立

假设(Yi,Xi,Ui)，i=1,…,n为来自变系数模型(1)的一组独立同分布样本.利用B样条基函数去近似模型(1)中的β(·).令B(·)=(B1(·),…,Bqn(·))T为m阶的B样条基，则每个函数系数βl(·)都可以用如下表达式近似：

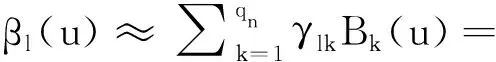
(2)

其中：γl=(γl,1,…,γl,qn)T是系数向量；qn=kn+m+1是基函数个数；kn为内节点的个数.基于以上近似，则模型(1)可写为

(3)

令πi=Ip⊗B(Ui)·Xi，Ip是p×p的单位矩阵.模型(3)可被改写为

(4)

则变系数模型的复合分位数函数为

(5)

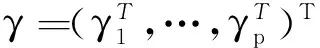
ρτk(x)=τkxI(x≥0)-(1-τk)xI(x<0)，

(6)

其中：τk=k/(q+1)；q为所取分位数点的个数；cτk是随机误差ε的τk分位点.

本文的目的是从模型(5)中识别出常系数变量和变系数变量以及系数为零的变量.设pλ′(·)为SCAD惩罚函数(Fan和Li[9])的一阶导函数：

(7)

其中，a>2，θ>0并且pλ(0)=0以及非负的惩罚参数λ.为了进行变量选择和参数识别，将以下目标函数最小化，

(8)

其中：

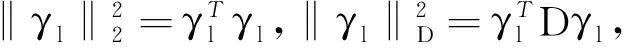
对于目标函数(8)来说，第一个惩罚pλ1(·)是用来控制模型的稀疏程度.显然，如果‖γl‖2被压缩为0，则βl(·)=0.从第二个惩罚函数可以看出

其中

fl={βl(U2)-βl(U1),…,
βl(Un)-βl(Un-1)}T.

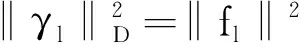
2 算法与调节参数的选取

2.1 算法

首先，本文采用MM算法，构造一个优化函数去逼近目标函数L(γ)，然后最小化优化函数.以L(γ)为基础，函数(5)能够被优化为

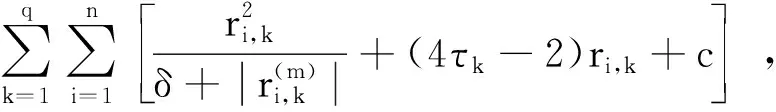
(9)

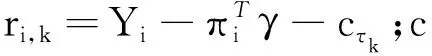
进一步，除去常数部分的目标函数Ln(γ)可以被近似替代为

(10)

为了提高局部二次近似方法的精确性，将

替换为

以及

替换为

其中:ϑ为扰动项(ϑ>0).关于ϑ取值可以参考文献[10].进一步利用牛顿迭代算法可以获得(10)的数值解.

2.2 参数的选取

为了实现这个算法，需要选择B样条的阶数m，内结点的个数kn以及两个惩罚参数λ1，λ2.对于变系数模型，通常使用低阶样条，所以本文使用三阶B样条(m=3)，由于B样条内结点的个数对参数估计不敏感，因此，本文取kn=[n1/(2m+3)]，其中[a]表示取值不超过a的最大整数.通过最小化BIC对λ=(λ1,λ2)进行选择，BIC的定义为

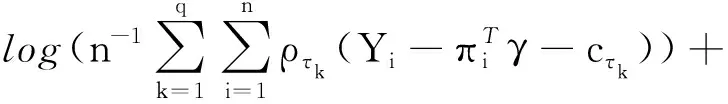
(11)

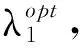
3 数据模拟

例1数据来源于以下部分线性变系数模型：

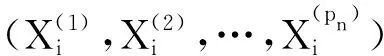
考虑以下3种误差分布：(1)标准正态分布N(0,1);(2)自由度为3的t分布t3;(3)Lognormal (0,1)分布.在模拟中，考虑n=200,300，重复模拟200次.由于复合分位数估计不依赖q的选取，所以本文考虑q=9.同时在数值模拟中对比以下两种方法：(1)惩罚最小二乘估计(PLS)；(2)惩罚分位数回归(PQR).考虑分位数τ=0.5，0.75，相应的估计记为PQR0.5、PQR0.75.同时为了说明PCQR估计的有效性，采用以下几个评价指标：

(1)均方误差平方根(Square root of average square errors,RASE)，其定义为

(2)正确识别零系数的平均个数：C.

(3)非零系数识别为零系数的平均个数：IC.

(4)正确识别变系数的平均个数：CV.

(5)正确识别常系数的平均个数：CC.

(6)正确识别真实模型的比率：CF.

(7)真实模型下估计的RASE：Oracle.

(8)惩罚估计的RASE：Penalized.

具体的数值模拟结果如表1所列.

从表1中可以得出以下结论：首先，当n=200，误差服从正态分布时，PLS的Oracle估计虽然具有最小的RASE，但是PCQR估计的CF是3种方法中表现最好的.当误差分布服从厚尾分布(t3、Lognormal)时，发现尽管PQR估计整体上都比PLS估计好，但是关于CF和RASE方面，PCQR估计表现最好，这也就意味着PCQR估计不仅比PLS估计稳健同时还比PQR估计有效.最后，随着变量的增加，PCQR估计选出真实模型的比率明显高于PLS和PQR且越来越来接近1.同时PCQR的Oracle估计具有最小的RASE，且惩罚下的RASE与 Oracle估计的RASE差距最小，这也表明本文的PCQR具有Oracle性质.

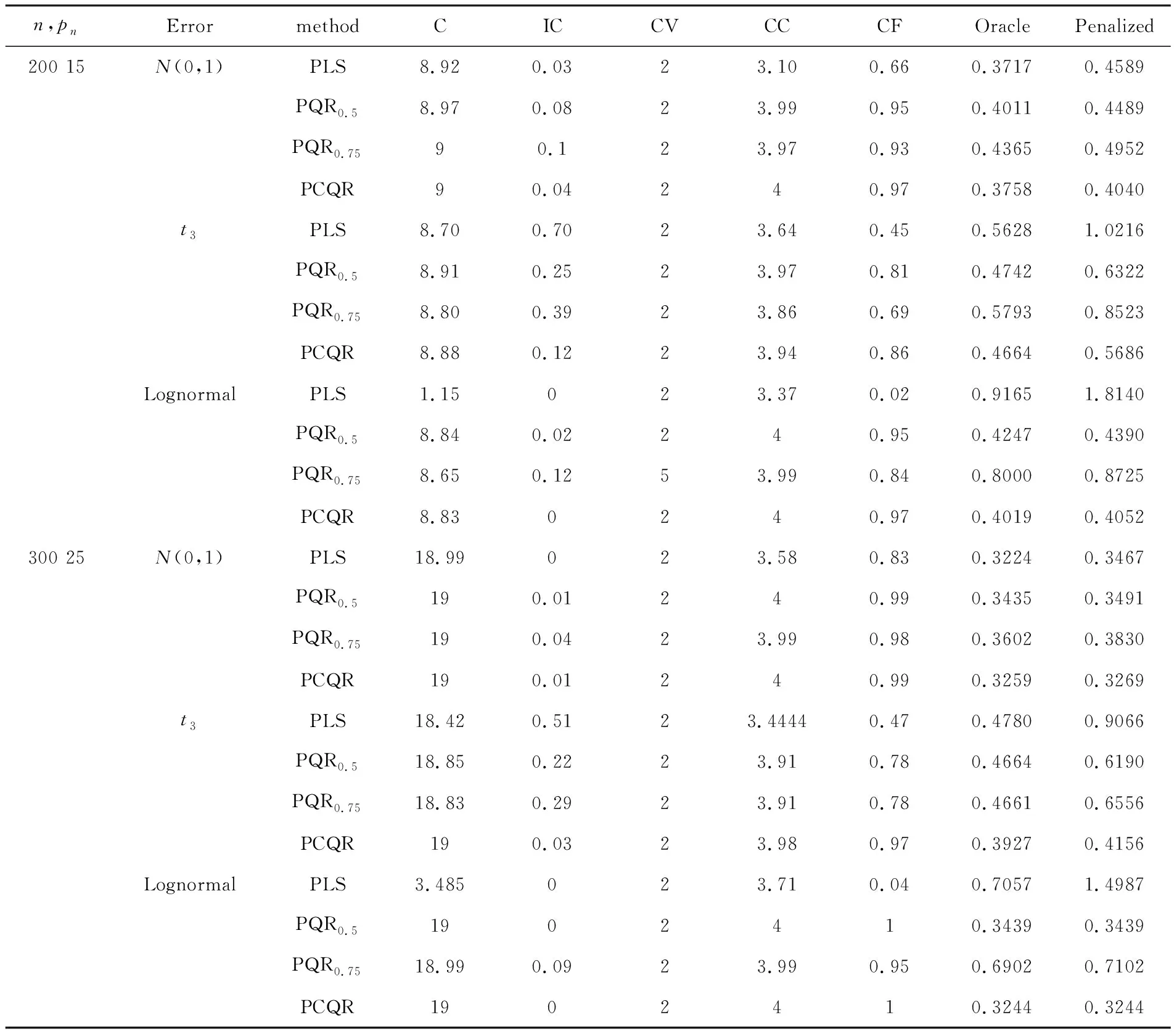
表1 例1的数值结果

4 实例分析

为了更好地验证PCQR方法的有效性，本节将所提方法运用到Boston住房数据中.根据Wang和Xia(2009)[11]的建议，将房子价格的中位数(medv)作为响应变量Y，地位较低人口占总人口的百分率(lstat)作为指标变量U，再将以下6个变量作为协变量X：镇上人均犯罪率(crim)、氮氧化合物浓度(nox)、每座住宅的房间数的均值(rm)以及在1940年之前建造的房屋所占比率(age)、房屋全值物业税率(tax)、镇上学生人数和老师人数的比率(ptratio).先将所有的协变量都看作变系数，用本文所提出的方法进行选择和识别.同时，将PCQR与PLS和PQR进行对比.为了检验模型的预测能力，将506个数据随机分为训练集(training data)和预测集(testing data)，其中300个数据作为训练集用于变量选择和参数估计，剩余的206个数据则看成是预测集用来评估模型的预测能力.本文利用MAPE(mean absolute prediction error)来衡量模型的外预测能力，其定义为

实验结果如表2所列.

重复模拟200次，用从6个变量中做变量选择后的平均个数(Size)刻画模型的复杂程度.若拟合效果越好，预测精度越高，则外预测(MAPE)越小.从表2的结果可以看出，PCQR的MAPE明显小于其余两种估计方法的MAPE，且模型的复杂程度低于其余两种方法，说明本文提出的估计方法的有效性.

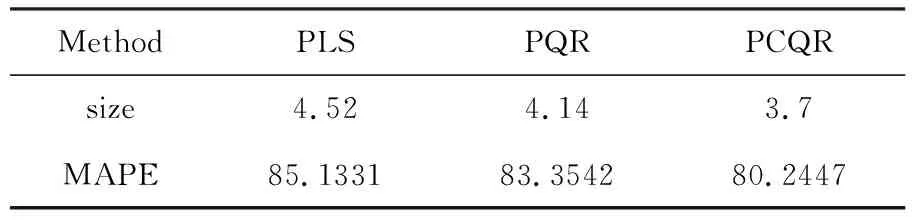
表2 基于200次重复，各种方法的MAPE

5 结语

本文针对变系数模型变量选择和结构识别问题，提出了能够同时对模型进行变量选择和结构识别的新方法.通过数值模拟分析，PCQR比现有方法更加稳健和有效.同时实证分析也说明PCQR比现有方法有更好的预测精度.