基于湿热环境-载荷试验的复合材料结构载荷测量方法研究

朱江辉

(1.中国飞行试验研究院，陕西 西安 710089；2.西北工业大学自动化学院，陕西 西安 710072)

0 引言

飞行载荷实测是飞机结构完整性验证过程中一项非常重要的内容。目前常用的方法有应变法和压力分步法[1]。压力分布法可直接对气动力在结构表面引起的压力分布进行测量[2-4]，但该方法目前仍具有实施复杂及维护成本高的特点。应变法是通过建立结构应变与载荷间的对应关系，从而得到飞行载荷的方法[5]。

随着先进复合材料在航空领域的应用越发广泛，复合材料结构载荷的测量精度直接关系到飞机设计的安全性和经济性，在军、民用飞机的设计环节起着非常重要的作用。复合材料结构的各向异性和湿热特性等，导致其载荷测量必然与较为成熟的金属材料结构存在一定的区别，直接影响到复合材料的载荷测量精度。石海波等[6]研究了复合材料垂尾受热应变激增的问题，表明复合材料的各项异性会影响载荷测应变电桥的热输出。郑起等[7]建立周期复合材料湿热效应的双尺度渐进展开模型，研究了周期性复合材料在湿、热、力耦合作用下的结构响应，但并未做试验验证。因此需要研究复合材料结构载荷测量应变计选型及改装工艺、湿热环境影响分析及修正方法等，以减少湿热环境对复合材料结构载荷测量的影响，提高载荷测量的精准度。

论文主要针对碳纤维复合材料结构的各向异性和湿热环境特性，通过复合材料翼面主承力结构典型材料体系和铺层形式的层压板和翼盒段试验件湿热环境-载荷理论研究和地面试验，开展载荷测量应变计选型与改装工艺研究和湿热环境对载荷测量应变计电桥响应的影响研究，掌握复合材料结构载荷测量湿热分析及修正方法，提高复合材料结构载荷测量精准度。

1 理论分析

通过在复合材料经典层压板理论的基础上加入湿热本构关系，考虑湿热条件导致层压板的性能退化，在计算模型中加入层压板刚度退化信息，对经典层压板理论进行修正，进而构建复合材料层压板在湿热力共同作用下的本构关系。

1.1 湿热环境下复合材料层压板响应预测模型

复合材料经典层压板理论中，层压板第k层的应力可通过(1)式表达：

(1)

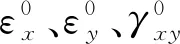
要使(1)式所表示的应力分量在层压板的侧面上精确的满足应力边界条件，在绝大多数情况下是十分困难的，只能使用圣维南原理，使层压板在全厚度的应力分量所合成的内力整体满足边界条件。

结合应力公式沿着层压板的整个厚度积分便可以得到这些合力与合力矩分量。由于沿着厚度方向各应力分量在各铺层之间不一定连续，而在一个铺层内却是连续分布的，所以分层再求和，可以得到：

(2)

式中：

(i，j=1，2，6)

(3)

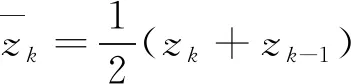
由于Bij的存在，层压板的面内力Nx，NY，Nxy可以产生弯曲和扭曲变形；而弯矩和扭矩Mx，My，Mxy可以产生面内伸缩和剪切变形。

湿热的变化会导致复合材料产生一定的应变变化，导致测量应变中不仅包含结构应变，还存在部分由湿度及温度变化引入的应变，因此需要对其进行研究修正。复合材料单层板的材料主方向湿自由应变可以通过(4)式表示：

(4)

其中，β表示材料的湿膨胀系数，符号C表示单层板的吸湿量，为单层板吸入水分后质量的和干燥状态下的质量比：

(5)

材料热膨胀导致的应变同湿膨胀一样，也通过引入热膨胀系数来表述，因此得到的单层板的材料主方向湿热自由应变为：

(6)

根据叠加原理，总应变为机械载荷引起的应变与湿热自由应变之和，即：

(7)

在考虑湿热变形情况下，正交各向异性复合材料的本构模型为：

(8)

在湿热环境下，复合材料的弹性模量和强度等性能下降。本项目引入Tsai提出的无量纲温度T*，其表达式如下：

(9)

采用混合定律计算材料的湿热膨胀系数、弹性模量、剪切模量以及泊松比，公式如下：

(10)

α2=Vf(1+vf)αf+Vm(1+vm)αm-(Vfvf+

Vmvm)α1

(11)

(12)

(13)

E11=Ef11Vf+EmVm

(14)

(15)

(16)

v12=Vfvf+Vmvm

(17)

式中：α为单层材料的热膨胀系数，β为单层板材料的湿膨胀系数，E为单向板弹性模量，G为单向板剪切模量，v为单向板的泊松比，下标m表示基体性能，下标f表示纤维性能。那么，湿热环境对纤维和基体性能的影响可以用T*的幂函数来近似表达，表达式如下：

(18)

1.2 载荷应变与环境应变的分离方法

对一般的应力应变曲线，湿热力共同作用时的应变应力曲线可表达为：

εMHT=kMHTσ+e

(19)

其中，kMHT为湿热力共同作用时测点的应变应力曲线斜率，εMHT为湿热力共同作用时测点的实测应变，e为湿热自由应变。

机械载荷单独作用时的应变应力曲线可表达为：

εM=kMσ

(20)

其中，kM为机械载荷单独作用时的应变应力曲线斜率，εM为载荷单独作用时的应变。

由实测应变得到载荷应变εM与环境应变εHT的表达式为：

(21)

εHT=εMHT-εM

(22)

基于以上理论，依据实测应变及有限元模拟结果来分离载荷应变与环境应变的方法分为两个步骤：

1)利用有限元软件分别模拟计算得到机械载荷单独作用时和湿热力共同作用时的应变应力曲线，得到它们的斜率kM和kMHT。

2)根据实际测得的应变εMHT，由公式(21)和公式(22)计算得到该状态下对应的载荷应变εM与环境应变εHT。

2 复合材料试验件制作及试验方案

2.1 复合材料层压板

分析常用的复合材料结构的材料体系和铺层形式，针对平尾复合材料体系和铺层形式，选择4种常用的典型铺层和4种某型飞机平尾载荷测量剖面梁和蒙皮铺层形式，共完成8种铺层的拉伸、压缩和剪切复合材料层压板试验件。层压板试件铺层形式见表1，复合材料层压板结构示意图见图1。

表1 层压板试件铺层形式

图1 复合材料层压板结构示意图

2.2 复合材料层压板结构载荷测量温度-湿度-机械加载试验

通过复合材料层压板结构载荷测量温度-湿度-机械加载试验，分析研究复合材料层压板拉伸、压缩和剪切载荷测量应变电桥响应的重复性和线性度，不同铺层、不同应变计、不同组桥方式等热输出规律以及载荷测量应变电桥响应系数随温湿度变化规律。对比研究复合材料结构载荷测量应变改装工艺，探索复合材料结构载荷测量温度修正方法。

复合材料层压板试验内容包括室温干态拉伸、压缩和剪切，高温干态拉伸、压缩和剪切，低温干态拉伸、压缩和剪切，23～-55 ℃纯温度干态试验，23～70 ℃纯温度干态试验，室温湿态拉伸、压缩和剪切，高温湿态拉伸、压缩和剪切等17个试验状态1008个工况。具体见表2。

表2 复合材料试件级环境试验工况

2.3 复合材料试验件应变改装

为了考查不同应变桥对响应的影响，针对复合材层压板进行了应变改装，复合材料拉伸试验件加装HBM复合材料应变全桥、中航电测钛合金应变全桥以及日本共和钛合金1/4桥，压缩试验件和剪切试验件均加装有HBM复合材料应变全桥和中航电测钛合金应变全桥。

表3 层压板与盒段件应变改装工艺方案

3 试验研究

3.1 复合材料层压板载荷测量湿热影响仿真结果分析

利用前述理论分别对不同铺层拉伸、压缩及剪切试验件进行了仿真计算，包括常温干态纯机械载荷计算及湿热力耦合计算，得到应力应变曲线，图2为铺层1拉伸试验件应力应变曲线。

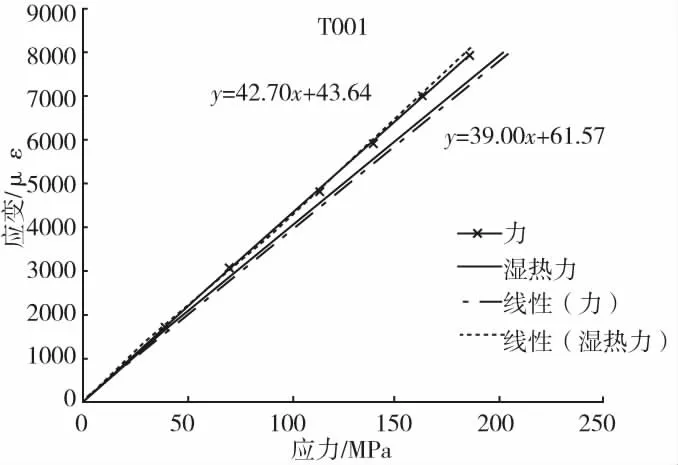
图2 铺层1拉伸试验件应力应变曲线

3.2 复合材料层压板温度-湿度-载荷试验研究

通过对室温、高温和低温干态以及室温和高温湿态拉伸、压缩和剪切试验数据分析，发现层压板载荷测量应变电桥响应线性度和重复性良好。图3给出低温干态和高温湿态拉伸试验载荷应变曲线，图中，H：HBM全桥，Z：中航电测全桥，H1：共和纵向应变1/4桥，H3：共和横向应变1/4桥。

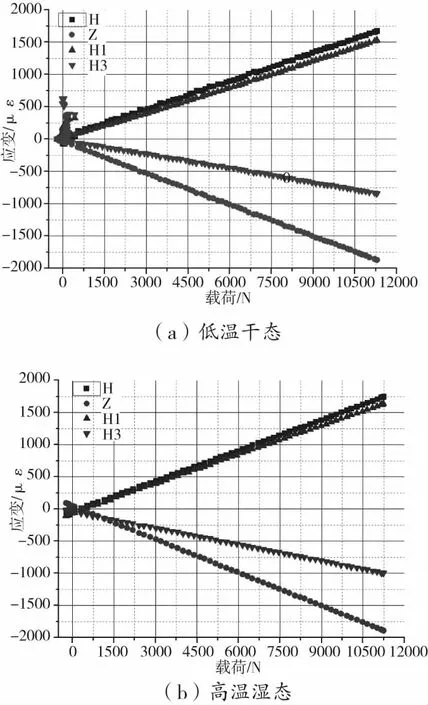
图3 低温干态和高温湿态拉伸试验A5T1试验件载荷应变曲线

通过对23～-55 ℃与23～70 ℃纯温度干态试验结果分析发现，在无机械载荷施加情况下，HBM应变电桥及中航电测应变电桥响应均随着温度的变化而变化，大部分应变电桥随温度变化的规律性较好，个别电桥在高、低温试验中随温度变化量值差别较大。在23～-55 ℃纯温度干态试验中，A5铺层剪切试验层压板低温试验应变电桥响应均在±30 με以内(图4)。23～70 ℃纯温度干态试验中，除了HBM应变电桥A5S6H和中航电测应变电桥A5S4Z响应较大以外，其他均在±20 με以内(图5)。1/4桥热输出相对于全桥稳定性差(图6)。

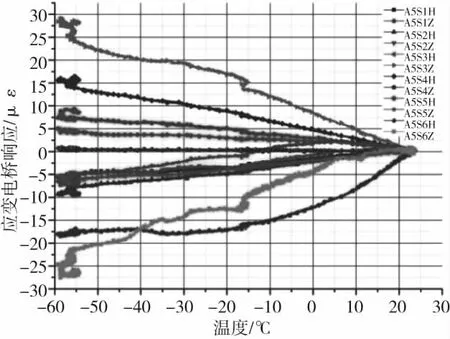
图4 A5剪切试验层压板低温试验结果

拉伸和压缩试验件A6铺层组中HBM应变计电桥热输出整体较大，而且当温度大于50 ℃时热输出异常波动，如图7和图8所示，而剪切则相对正常，考虑为不同铺层复合材料热膨胀系数、厚度等参数不同，A6铺层为非对称铺层且厚度最大，厚度越大铺层不对称时材料性能不均匀性更明显。

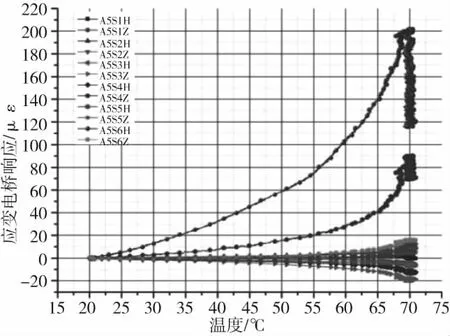
图5 A5剪切试验层压板高温试验结果

图6 纯温度试验应变全桥和1/4桥热输出响应

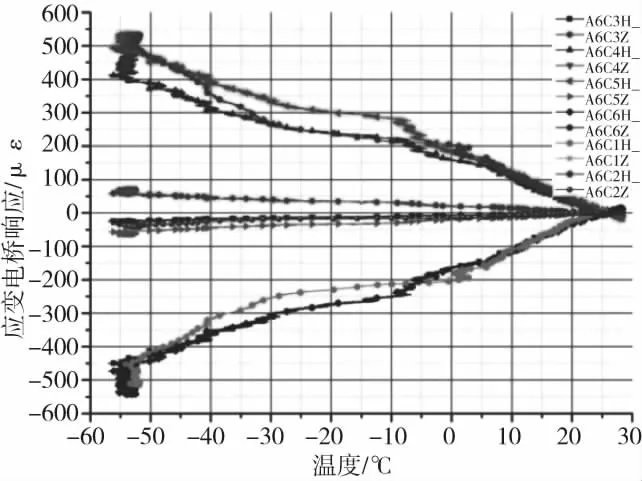
图7 压缩试验件A6低温试验结果

剪切试验件上的电桥温度响应相对拉伸及压缩试验件上的电桥热输出较小，分析复合材料层压板的铺层方式，发现8种铺层方式的试验件中±45°方向的纤维铺层比例均为1∶1，而0°/90°的纤维铺层比例各异。考虑到0°及90°铺层对±45°方向材料性能影响基本相同，因此±45°方向材料性能相同，应变计组全桥测量剪力时，能够减少热输出的影响。

图8 压缩试验件A6高温试验结果

拉伸、压缩试验件上粘贴的拉压全桥的热输出相对较大。以低温试验中压缩试件上的应变全桥为例，可以看到除A6铺层组的HBM全桥外，其余电桥的热输出均在200με以下。电桥的热输出随复合材料试验件的0°与90°方向铺层层数差的增加而增加，如图9所示。即复合材料在拉压电桥所测得两个方向上的热膨胀差异越明显，其导致的温度响应也就越大。

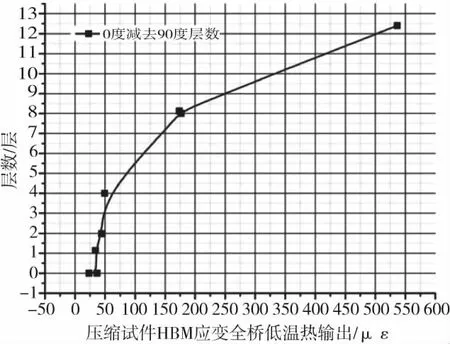
图9 应变电桥的热输出与层压板0°与90°层数差关系

针对每个试验件，计算其应变电桥的响应系数，然后按照各种铺层的拉伸、压缩和剪切试验件计算得到6个试验件的常温、高温和低温干态以及室温和高温湿态试验应变电桥响应系数的平均值，为了便于对比分析，同时给出了高温和低温干态及室温和高温湿态试验响应系数的平均值相对于室温干态试验结果的变化比值。结果表明，HBM应变电桥比中航电测应变电桥相对变化比值随温度变化趋势更合理，大部分电桥测量值随温度升高而升高(图10)。

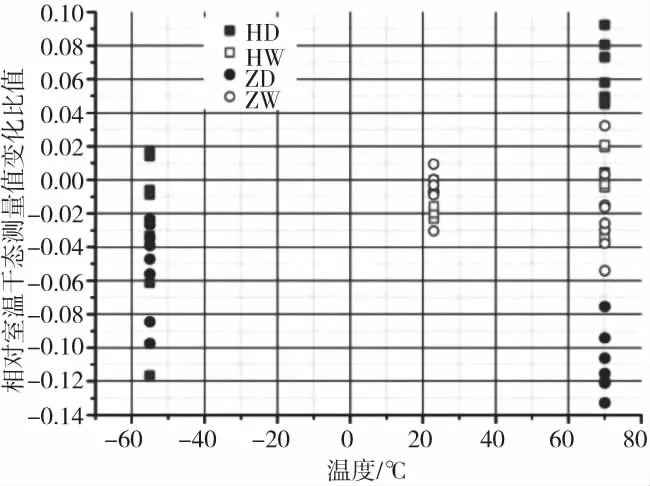
图10 层压板拉伸试验应变全桥响应系数相对变化比值

3.3 基于飞行实测数据的复合材料结构载荷测量热输出修正方法

该方法主要基于复合材料层压板和盒段件载荷测量应变电桥热输出与温度成线性关系提出的。首先统计分析飞行实测应变电桥响应与测载部位实测温度的相关性，对于民机来说，气动加热影响小，如果没有实测部位温度可以用高度或总温代替，对于相关性较大的应变电桥，将应变电桥响应与温度或高度进行拟合，得到温度与应变电桥响应的关系式，将实测温度或高度变化量代入该关系式即可得到应变响应的修正量。将此修正量代入对应载荷方程中，就得到实测载荷的修正量。

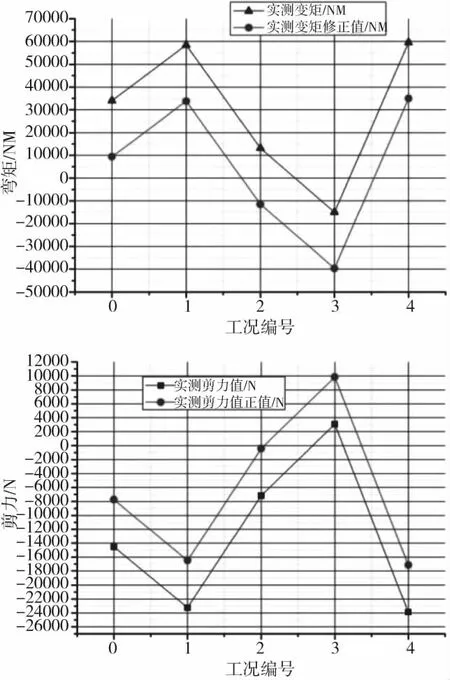
图11 某飞机飞行状态下修正前后实测载荷曲线

4 结论

论文在复合材料经典层压板理论的基础上加入湿热本构关系，考虑湿热条件导致的性能退化，建立了一套湿热环境下复合材料层压板弹性响应的预测模型，进而提出了一种在实际工程应用中分离环境应变与载荷应变的方法。

利用该方法分别对复合材料层压板和盒段试验件湿热环境-载荷试验进行仿真计算，得到了湿热力耦合作用下和力单独作用下的应力应变，为复合材料层压板及盒段试验件温度-湿度-机械加载地面试验及其结果分析提供依据。最后，通过层压板地面试验充分验证了该方法的有效性，并将其在飞行试验数据中进行了应用，为复合材料结构载荷测量提供重要理论分析手段。