基于田口法的VS-MFxLMS算法优化及其在船舶舱室主动降噪上的应用
夏雪宝, 明志茂, 赵可沦, 张 波
(广州广电计量检测股份有限公司, 广东 广州 510000)
0 引 言
船舶制造业作为我国制造业重要的支柱产业之一, 急需向高端制造转型, 提升船舶设计建造的水平. 舱室的声环境系统是直接面对使用人员的一种重要船用系统. 船舶各个舱室中集成了众多的电气化设备, 这些设备在狭小的空间中不可避免会发生共振, 造成严重的空气噪声干扰, 这给船上人员的身心健康造成了不良影响.
对于噪声的控制方法主要分为被动控制方法和主动控制方法, 其中, 被动噪声控制方法是利用隔声、 吸声材料或消声结构设计来抑制中高频噪声, 而对于低频噪声往往降噪效果不佳. 此时, 主动噪声控制方法相比于被动噪声控制方法更为有效, 并且具有结构紧凑、 可实现模块化设计、 便于安装等优点, 目前已被广泛应用于汽车、 工业、 家电等领域.
1 主动控制降噪技术发展现状
在现有主动降噪算法中, 著名的Filtered-x LMS (FxLMS) 算法[1-2]在LMS算法的基础上考虑了次级路径对噪声控制的影响, 因其具有更好的稳定性和实用性而被广泛应用[3]. 由于FxLMS引入了次级路径, 也导致了算法延时的增加而使得其收敛速度变慢. 因此, Gomathi等[4]提出了一种基于反正切函数的变步长VS-FxLMS算法, 可以有效地改善这一问题. 对于非稳态冲击噪声信号, FxLMS算法可能会失稳[5], 而MFxLMS算法[6]因其算法简单且具有更好的鲁棒性和收敛性而被应用于非稳态噪声主动控制领域. 为了进一步提高MFxLMS算法的收敛性, 张帅等[7]在文献[4]的基础上提出了变步长VS-MFxLMS算法, 并针对汽车车内非稳态噪声进行有源主动控制.
综上所述, 变步长是控制主动降噪算法收敛性的有效手段. 变步长控制参数选取主要以试错法或经验法为主, 需要大量的时间、 人力及物力. 因此, 本文在VS-MFxLMS算法的基础上, 提出了一种更加简洁的归一化反正切变步长控制函数, 利用田口法对变步长控制参数进行优化分析, 并对船舶舱室内非稳态噪声进行主动控制仿真和试验分析.
2 船舶舱室噪声特性分析
2.1 船舶舱室噪声来源
船舶舱室内的噪声主要来源于船舶运行时的主机、 辅机、 空调系统以及螺旋桨等. 根据噪声的产生机理和传播途径可以将船舶舱室噪声分为两类.
2.1.1 空气辐射噪声
对于存在声源的船舶舱室, 噪声的声压级主要取决于声源的辐射, 舱室围护结构的声辐射是次要的; 而在其他舱室内, 空气噪声取决于围护结构的声辐射. 空气噪声的声振动源主要有船用机械以及某些通风管道及管路.
此类噪声主要包括: 动力装置的噪声、 辅助机械噪声、 通风空调系统噪声等.
2.1.2 船体结构振动辐射声
辐射声振动源包括螺旋桨和激励船体表面的水流. 在这种情况下, 所有舱室的噪声均取决于传播声振动的围护结构. 这部分还包括安装结构振动的辐射声振动源, 这组振源有某些空气管道和其他管路. 由于安装结构(板架、 隔壁、 船体外板)比振源表面大得多, 安装结构变成了主要辐射体.
此类噪声主要包括: 螺旋桨引发的噪声、 船体振动噪声等.
2.2 船舶舱室噪声特性
本文主要通过主动控制算法对船舶舱室内的低频噪声进行控制, 故在此仅对舱室内1 000 Hz以下的噪声进行研究.
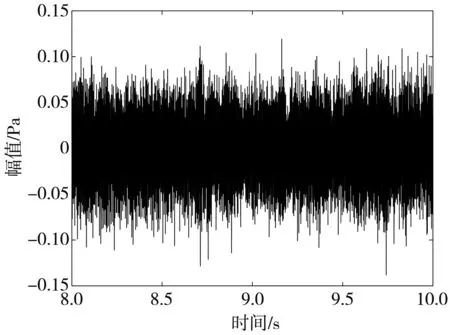
图 1 为船舶舵机机舱内采集到的数据, 取6.0 s~8.0 s 内的稳定数据进行分析.
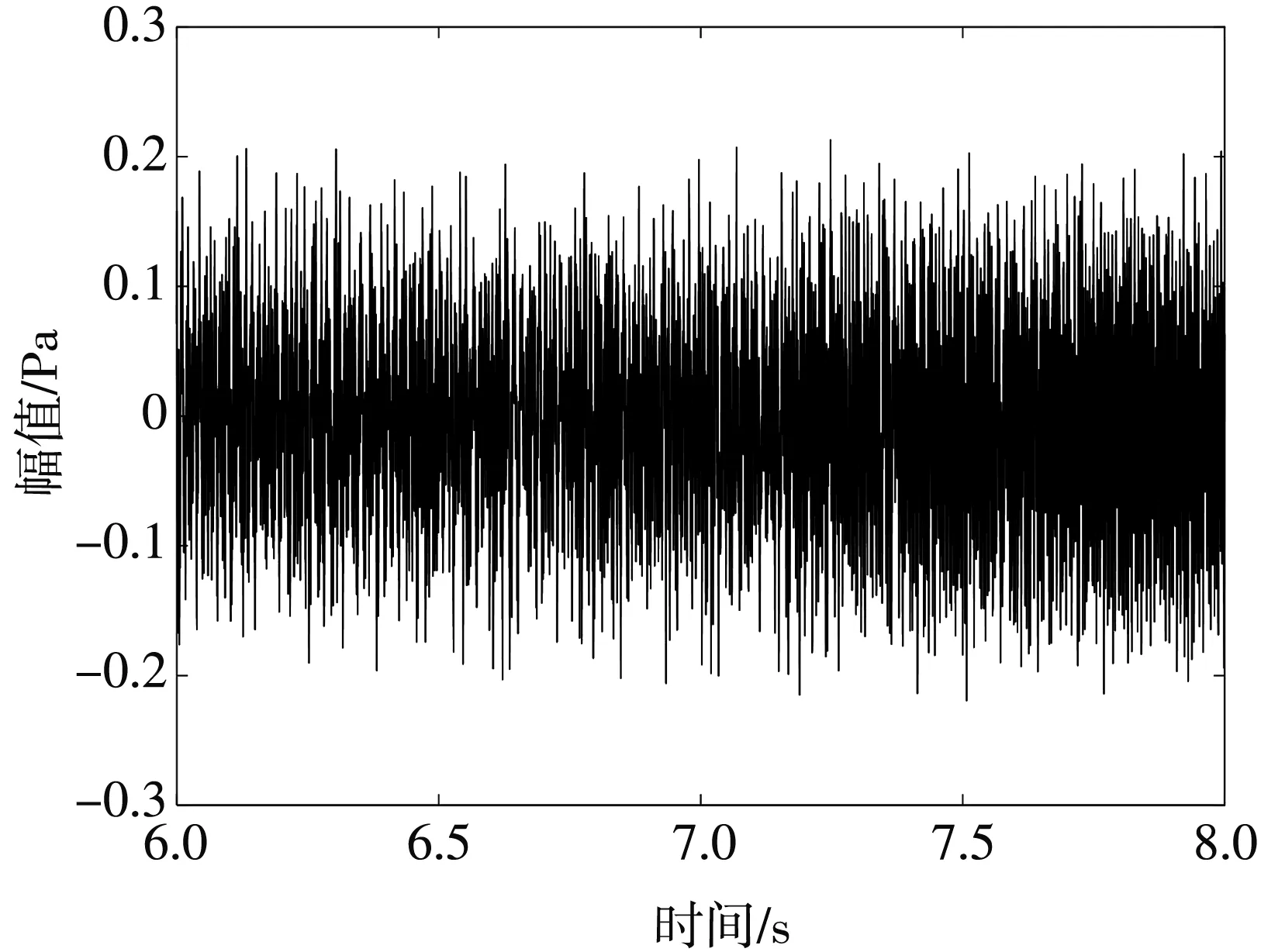
图1 舵机室噪声时域图Fig.1 Time domain diagram of noise in the steering engine room
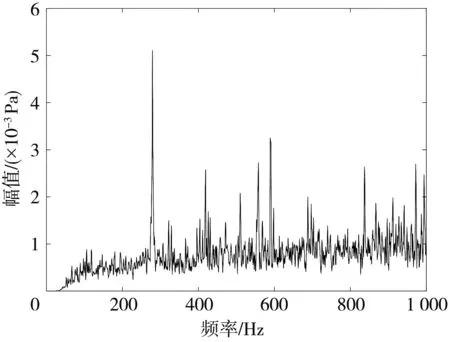
通过傅里叶变换将噪声信号由时域转化为频域, 得到图 2 所示的舵机室噪声频域图.
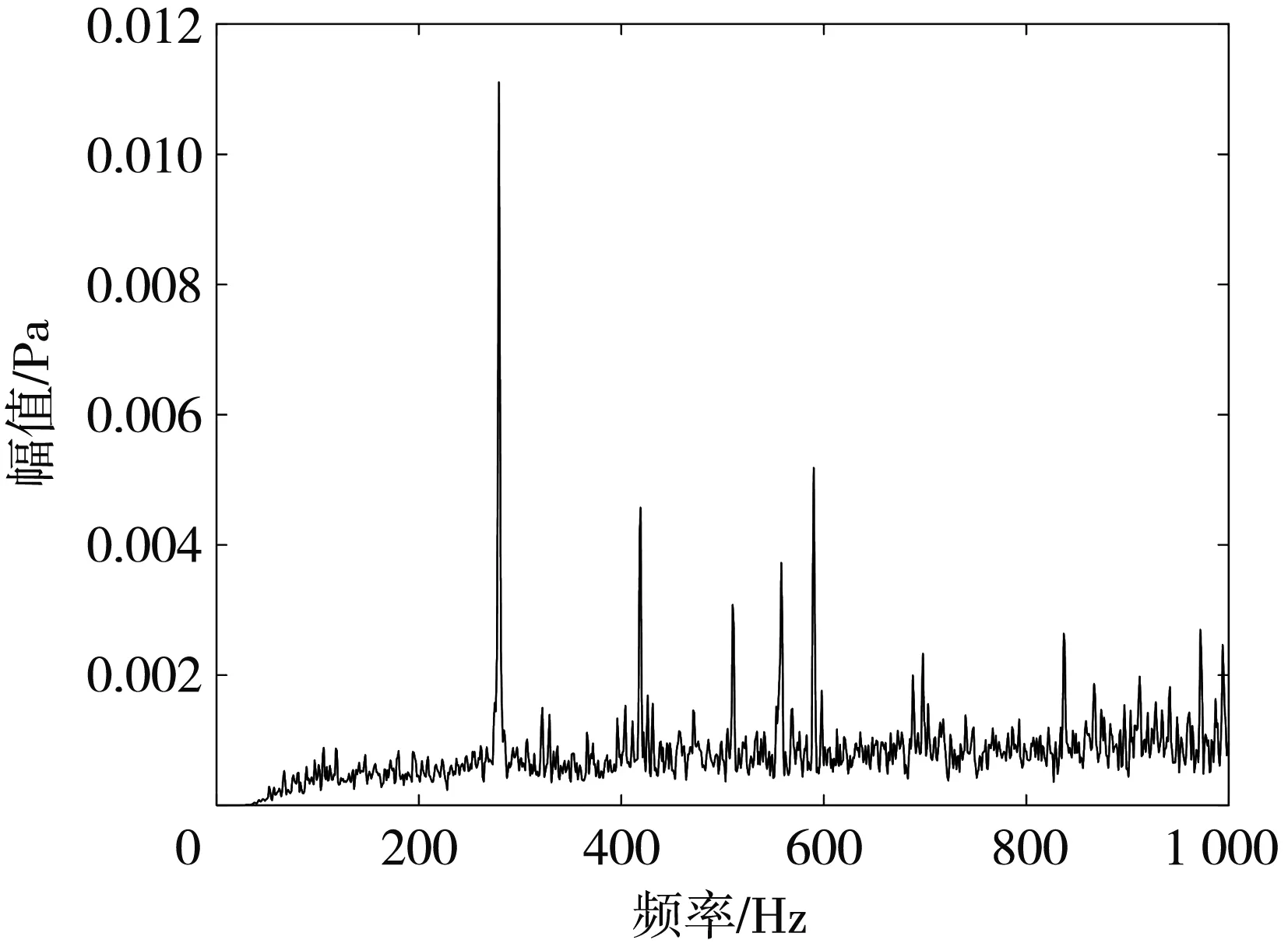
图2 舵机室噪声频域图Fig.2 Frequency domain diagram of the noisein the steering engine room
从图 2 可以看出, 舵机舱室的噪声频率在280 Hz, 420 Hz, 580 Hz处均出现了较高的峰值, 这些峰值主要由舵机工作引起. 通过计算得到舵机舱室的声压级为72.89 dB(A)
3 MFxLMS算法介绍及优化方法
3.1 MFxLMS算法介绍
图 3 为MFxLMS算法流程图, 其中P(z)为系统的初级路径;S(z)为系统的次级路径;W′(z)为LMS滤波器系数;S′(z)为系统辨识的次级路径, 即S(z)的估计;x(n)为参考信号;d(n)为参考信号经初级路径后得到的期望信号;error为次级信号与期望信号抵消后产生的残差信号,
error=d-yf(n),
(1)
y(n)为次级信号,yf(n)为y(n) 经次级路径滤波后的信号;xf(n)为x(n)经次级路径滤波后的信号;y(n)为xf(n)经LMS滤波器滤波后的信号;e(n) 为LMS系统误差信号,
e(n)=error+yf(n)-y′(n).
(2)
LMS滤波器系数可按以下公式进行更新
W(n)=W(n-1)+u(n)·
(e(n-1)·xf(n-1)).
(3)
根据LMS算法可知, 步长参数u(n)的变化范围为
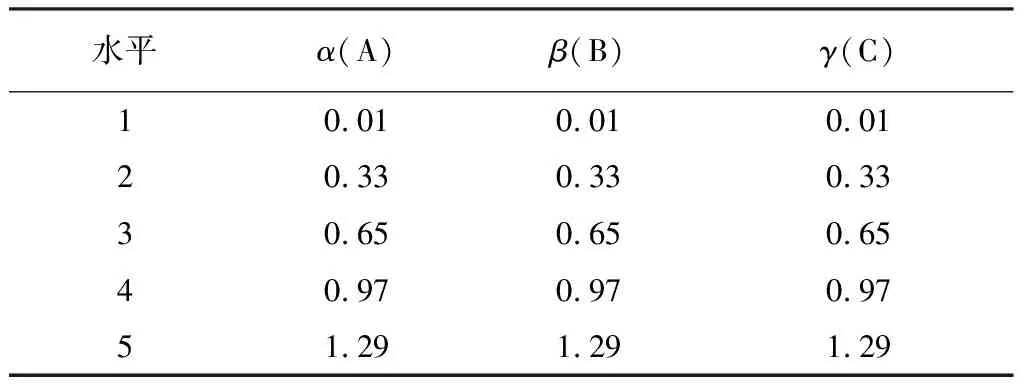
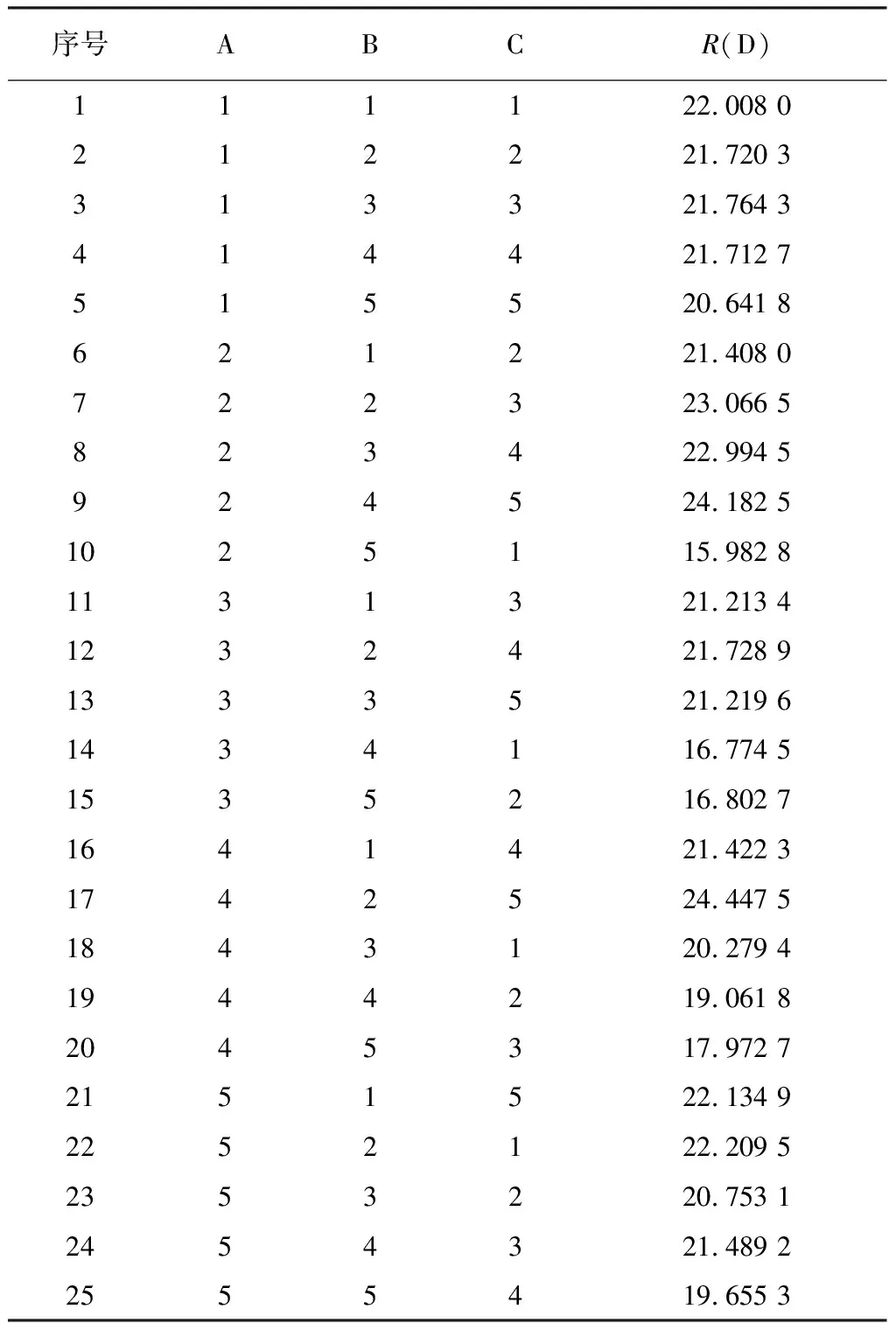
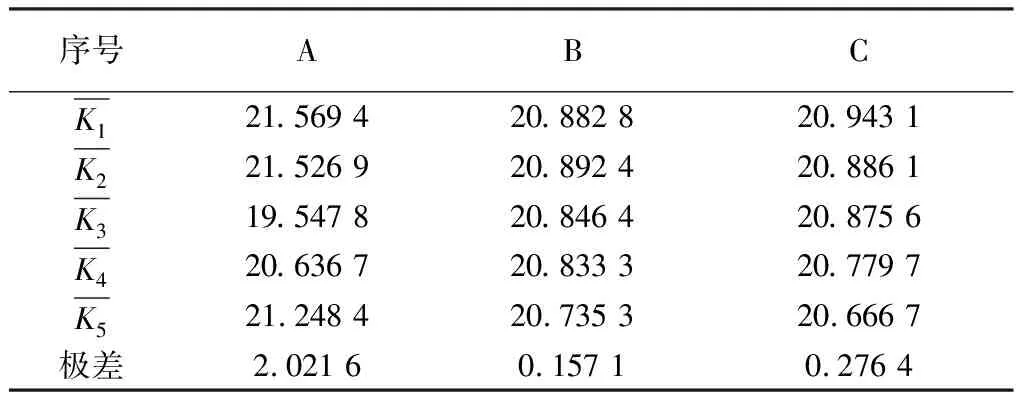
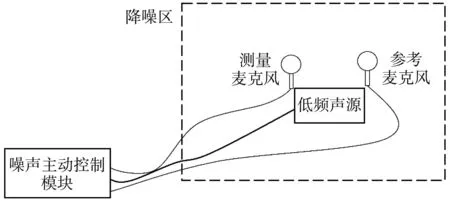
0 (4) 式中:Pxf=E(xf(n)2). 图3 MFxLMS算法流程图Fig.3 MFxLMS algorithm flow chart 张帅等[7]在文献[4]基础上提出了新的变步长控制函数, 如式(5)所示. 其中, 式(5)为了避免分母为0, 引入了(1+xf(n)2)作为分母, 但这样会影响归一化的效果. (5) xf(n)=S′(n)·x(n). (6) 通过仔细研究式(6)可以发现, 只有当次级路径系数S′(n)和x(n)分别或同时为0时,xf(n)才能为0, 而在实际工程应用中,S′(n)和x(n) 不可能分别或同时为0, 即xf不可能为0. 因此, 本文在文献[4]和文献[7]的基础上提出如下更加简洁的归一化反正切变步长控制函数. (7) 对于上述过程, 即使给定归一化反正切变步长控制函数, 由于α,β和γ3个变量的存在, 需要大量的调试和试错才能找到较为合适的参数组合.为了解决这一问题, 本文提出了基于田口法的实验设计, 对α,β和γ进行优化分析. 田口法由田口玄一博士提出, 旨在多参变量以及变量范围一定的情况下通过正交试验设计的方式寻求最优参数组合[8]. 田口法需要一种信噪比作为目标函数, 而主动降噪性能评价指标也是信噪比, 因此, 将田口法用于优化归一化反正切变步长控制函数非常合适. 田口法中需要明确以下概念: 1) 影响因素, 即会对试验结果产生影响的输入参数, 这里的影响因素为α,β和γ. 2) 因素水平, 即影响因素的取值范围, 以一定规则离散取值. 3) 评价指标, 即对试验结果的量化评价. 信噪比是评价主动降噪性能的重要指标, 田口法中评价正交试验结果优劣的指标以“信噪比”表示. 虽两者具体含义不同, 但可以把主动降噪后的信号信噪比作为正交试验结果的目标函数, 当作归一化反正切变步长控制函数参数优化选取的评价指标. 根据在船舶舵机机舱测得的噪声信号, 通过基于田口法的MFxLMS算法, 在满足步长参数变化范围的前提下, 构建L25(53)形式的正交试验表.其中,L表示标准型正交试验表, 25表示试验方案个数, 5表示影响因素的水平数, 3表示影响因素个数. 所得因素水平表和正交试验表如下. 表 1 列出了α,β和γ3个变量分别取0.01, 0.33, 0.65, 0.97以及1.29时的所有情况. 表 2 为根据正交试验表列出了α,β和γ3种变量存在5种水平时在正交试验下的所有组合, 共25组. 并分别算出了信噪比R(D)值, 信噪比越大, 降噪效果越好. 表 1 因素水平表Tab.1 Factor level table 表 2 正交试验表Tab.2 Orthogonal test table 表 3 为根据田口法思想将表2中的每个因素对应的所有水平对应的信噪比进行算术平均求解, 如第1行第1列为表2中所有α为1时对应的信噪比的平均值. 对于信噪比这个评价指标而言, 其值越大说明主动降噪效果越好. 通过极差分析, 对试验结果进行处理, 处理结果如表 3 所示. 表 3 最优结果分析Tab.3 Optimal result analysis 由结果分析可得, 对于影响因素α, 其对应水平1为最佳; 影响因素β的最佳水平为2; 影响因素γ的最佳水平为1.故最优参数组合为A1B2C1. 根据以上结果对舵机舱室噪声进行主动控制. 测试示意图如图 4 所示. 图4 降噪系统示意图Fig.4 Schematic diagram of noise reduction system 将噪声主动控制系统置于舵机舱室中, 对降噪区的噪声进行采集得到如下结果. 图 5 所示为测量麦克风采集到的舵机舱室中的时域信号. 图5 舵机室噪声时域图(降噪后)Fig.5 Time domain diagram of noise in the steeringengine room(after noise reduction) 从图 5 可以看出, 当降噪系统开始正常工作后, 降噪区域内的噪声相比于未降噪前的声压有明显的降低. 通过傅里叶变换得到降噪后的频域曲线, 如图 6 所示. 图6 舵机室噪声频域图(降噪后)Fig.6 Frequency domain diagram of noise in the steeringengine room(after noise reduction) 从图 6 可以看到, 由舵机工作时引起的 280 Hz、 420 Hz、 580 Hz等频率的噪声依然存在, 但与图2未降噪前的噪声相比, 幅值有较为明显的降低. 经过计算, 降噪后的声压级为67.73 dB(A), 较未降噪前下降了约5 dB(A). 针对FxLMS算法现有的问题, 本文提出一种更加简洁的归一化反正切变步长控制函数, 利用田口法对变步长控制参数进行优化分析. 最后通过优化后的FxLMS算法对船舶舱室内非稳态噪声进行主动控制仿真试验分析, 能够快速获得船舶舱室噪声主动降噪中步长控制函数的最优参数组合. 并在舵机舱室内进行降噪实验, 结果为降噪区域内的噪声下降了5 dB(A).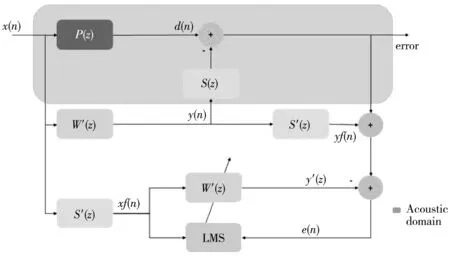
3.2 田口法控制函数参数优化分析
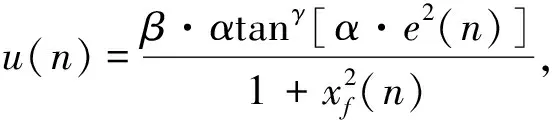
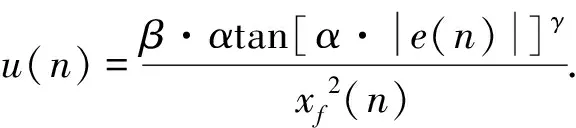
4 MFxLMS算法在船舶舱室主动降噪的应用
5 船舶舱室主动降噪结果
6 结 论

