LaNi0.95Fe0.05O3磁性粒子的制备及其对水中甲基橙的吸附动力学

陈 蕾，余传明

（1.湛江科技学院，广东湛江 524094；2.广东海洋大学化学与环境学院，广东湛江 524088）

我国水环境污染与水资源短缺问题正面临着严峻的形势。据国家生态环境部发布的《2019 中国生态环境状况公报》显示，2019 年全国直排入海污水排放总量为801 089 万t，其中工业污水排放量居第二位。印染废水是工业污水的主要种类之一，水质成分复杂，具有色度高、有毒有害物质多、可生化性差等特点，其中的难降解有机化合物难以通过常规的生物处理方法去除。甲基橙是一种偶氮类有色化合物，在工业生产和使用过程中容易进入水体，是印染废水中具有代表性的污染物之一，长期接触会导致机体微生物群基因突变。

目前印染废水的处理方法主要有萃取法［1-2］、生物法［3-4］、吸附法［5-7］、化学氧化法［8-9］、混凝法［10-11］、高级氧化法［12-15］以及各种联用方法［16-17］，其中吸附法由于具有投资小、周期短、操作简便、效率高、不产生二次污染等优点，逐渐成为一种经济有效且极具发展潜力的染料废水处理方法。本实验采用凝胶-燃烧法制备一种具有钙钛矿混晶结构的磁性吸附剂，以甲基橙模拟印染废水为研究体系，探究该吸附剂对甲基橙的吸附性能以及动力学行为。

1 实验

1.1 材料与仪器

材料：硝酸镧［La(NO3)3·6H2O］、柠檬酸、甲基橙、硝酸铁［Fe(NO3)3·9H2O］、氯化镍（NiCl2·6H2O）（分析纯，上海麦克林生化科技有限公司），无水乙醇（分析纯，国药集团化学试剂有限公司）。仪器：高灵敏度Zeta PLAS 电位及粒度分析仪（美国布鲁克海文仪器公司），JEM-7500F 场发射扫描电子显微镜（日本电子株式会社），Nicolet 460 傅里叶变换红外光谱仪、Escalab 250Xi X 射线光电子能谱仪（美国赛默飞世尔公司），ASAP2020M+C 全自动微孔物理化学吸附仪（美国Micromeritics公司），D8 Advance X射线衍射仪（Cu靶，2θ=5°～90°，德国布鲁克公司），SQUID-VSM 磁学测量系统（美国Quantum Design 公司），756S 紫外-可见分光光度计（上海棱光技术仪器有限公司）。

1.2 LaNi1-xFexO3粒子的制备

以LaNi0.95Fe0.05O3为例，按化学计量比分别称取4.330 g La(NO3)3·6H2O、2.258 g NiCl2·6H2O 和0.201 g Fe(NO3)3·9H2O，置于60 mL 乙醇水溶液［V（乙醇）∶V（水）=2∶1］中，搅拌溶解后加入柠檬酸，搅拌溶解后继续超声分散10 min，再于70 ℃下搅拌至出现凝胶状，将凝胶冷冻过夜，于冷冻干燥机中干燥48 h 获得干凝胶样品，将干凝胶样品置于马弗炉中600 ℃煅烧3 h，冷却至室温后研磨成粉，得到LaNi0.95Fe0.05O3样品。按类似方法合成不同Fe3+掺杂量的LaNi1-xFexO3（其中，x=0，0.05，0.10，0.20，0.40，0.60，0.80，1.00）粒子，记为样品1～8。

1.3 吸附实验

1.3.1 实验方法

以10 mg/L 甲基橙溶液模拟印染废水，准确称取0.100 0 g 吸附剂于100 mL 甲基橙溶液中，于设定温度的水浴中避光搅拌一定时间，用注射器取少量溶液，通过滤膜滤去固体吸附剂得到澄清溶液，以去离子水为参比，测试吸光度。

1.3.2 吸附等温线模型

选择Langmuir 模型和Freundlich 模型绘制吸附剂对甲基橙的吸附等温线。

Langmuir模型方程如下：

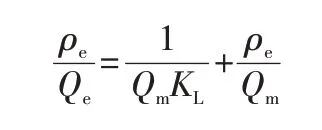
Freundlich 模型方程如下：

1.3.3 吸附动力学模型

常采用准一级和准二级动力学方程来描述和分析溶液中的吸附过程，用Elovich 方程描述包括一系列反应机制（表面络合交换、静电吸附、表面扩散和内部微孔扩散等）的过程，用Webber-Morris 颗粒内扩散模型方程分析扩散机理。

准一级动力学方程如下：

准二级动力学方程如下：

Elovich 动力学模型方程如下：

Webber-Morris 颗粒内扩散模型方程如下：

式中：Qt为t时刻的吸附量，mg/g；Qe为准一级动力学模型的平衡吸附量，mg/g；K1为准一级动力学模型的吸附速率常数，mg/（g·min）；Q2为准二级动力学模型的平衡吸附量，mg/g；K2为准二级动力学模型的吸附速率常数，g/（mg·min）；β为Elovich 动力学吸附速率常数，mg/（g·min）；α为常数；Kip为颗粒内扩散速率常数，mg/（g·min1/2）；C为常数。

1.4 回收实验

合并实验溶液，离心，收集固体粒子。通过2 种方法分别对吸附剂进行回收：（1）将吸附剂粒子置于100 mL 10 mmol/L 盐酸和去离子水中置换3次使吸附剂重生；（2）将粒子置于400 ℃马弗炉中煅烧实现重生，再参照1.3.1进行二次利用，测试平衡吸附量。

2 结果与讨论

2.1 表征

2.1.1 XRD

由图1 可以看出，LaFeO3粒子形成了典型的钙钛矿结构，其衍射峰位置及强度与标准PDF 卡（No.00-75-0541）的衍射峰一致，属于立方晶系。随着Ni3+掺杂量的增加，LaNi1-xFexO3粒子的衍射谱线出现杂峰，这是由于Ni3+半径（60.0 pm）比Fe3+半径（64.5 pm）小，部分取代造成了晶格收缩，当n（Ni3+）∶n（Fe3+）大于等于6∶4 时，钙钛矿结构崩坏，样品衍射峰出现分裂，发生晶格畸变。

图1 样品的XRD 图谱

2.1.2 XPS

图2 为LaNiO3、LaNi0.95Fe0.05O3和LaFeO3粒子的X射线光电子能谱全谱图，证实了LaNi0.95Fe0.05O3中La、Ni、Fe、O 4种元素的存在。

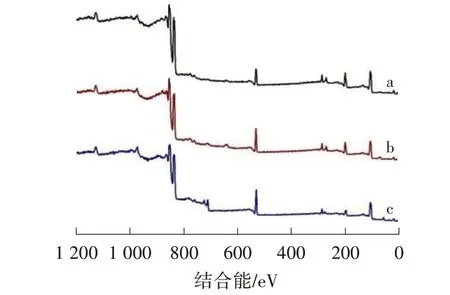
图2 LaNiO3（a）、LaNi0.95Fe0.05O3（b）和LaFeO3（c）的X 射线光电子能谱图

2.1.3 SEM

由图3 可知，LaNi0.95Fe0.05O3粒子为无规则颗粒，粒子表面具有圆形粗糙结构，通过低温氮气等温吸附-脱附分析，测定LaNi0.95Fe0.05O3粒子的比表面积为14.15 m2/g，平均粒径为423.9 nm。

图3 LaNi0.95Fe0.05O3的SEM 图

2.1.4 Zeta电位和粒径分布

由图4 可以看出，LaNi0.95Fe0.05O3粒子的Zeta 电位为24.8 mV，平均粒径为458.7 nm（与BET 法测试结果基本一致）。

图4 LaNi0.95Fe0.05O3的粒径分布及Zeta 电位分布图

2.1.5 FT-IR

由图5 可以看出，LaNiO3、LaNi0.95Fe0.05O3和LaFeO3都在561 cm-1处出现了钙钛矿的特征吸收峰，LaNiO3以及LaNi0.95Fe0.05O3在709 cm-1处的吸收峰为Ni—O 的伸缩振动峰。

图5 LaNiO3（a）、LaNi0.95Fe0.05O3（b）和LaFeO3（c）的FT-IR 图谱

2.2 影响甲基橙吸附性能的因素

2.2.1 样品选择

由图6 可以看出，样品2（LaNi0.95Fe0.05O3）对甲基橙的吸附率最高，为91.85%。这是由于Fe3+、Ni3+共混的LaNi0.95Fe0.05O3导致LaFeO3钙钛矿的晶型缺陷，同时，部分Fe3+和Ni3+被还原为Fe2+和Ni2+，形成的FeO和NiO 氧化物增大了晶体的不规则度和比表面积，有利于提高粒子的表面吸附能力。此外，粒子在水溶液中显示正电性，有利于对阴离子型染料的吸附。

图6 样品对甲基橙的饱和吸附率

2.2.2 样品质量

通过分光光度法测试了不同质量吸附剂对甲基橙的平衡吸附量，结果如图7 所示，吸附剂质量与平衡吸附量之间显示出良好的线性关系（相关系数R2=0.996），吸附剂的平衡吸附量为0.940 mg/g。

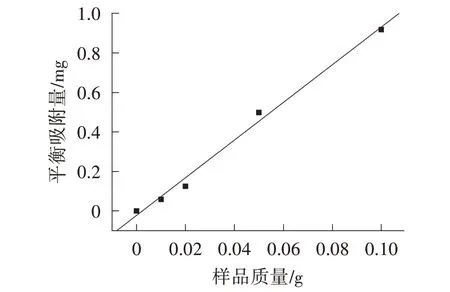
图7 LaNi0.95Fe0.05O3质量与平衡吸附量的关系曲线

2.2.3 温度

由图8 可以看出，在前5 min 内，吸附速率快，显著高于传统吸附剂［5，18-19］，并且在10 min 左右达到吸附饱和。在25、30 ℃条件下，LaNi0.95Fe0.05O3对甲基橙的吸附能力相近，随着温度的升高，LaNi0.95Fe0.05O3对甲基橙的吸附能力逐渐降低。表明高温不利于LaNi0.95Fe0.05O3对水中甲基橙的吸附。

图8 不同温度下LaNi0.95Fe0.05O3对甲基橙的吸附曲线

25 ℃时LaNi0.95Fe0.05O3对水中甲基橙的吸附效果如图9 所示，10 min 后，甲基橙溶液由橘黄色褪至几乎无色，基于吸附剂本身具有磁性，利用磁铁可以实现吸附剂与澄清液的快速分离，既提高了分离效率，又便于吸附剂的重复利用。

图9 LaNi0.95Fe0.05O3对甲基橙的吸附效果示意图

2.3 吸附热力学

为了进一步探索染料分子在吸附剂与水的固液界面处的吸附行为，根据25 ℃、不同吸附剂用量条件下吸附平衡时甲基橙分子在两相中的质量浓度，以Langmuir 和Freundlich 等温吸附模型拟合回归方程，结果如图10所示，相关模型参数如表1所示。

表1 Langmuir 和Freundlich 等温吸附模型回归方程和参数

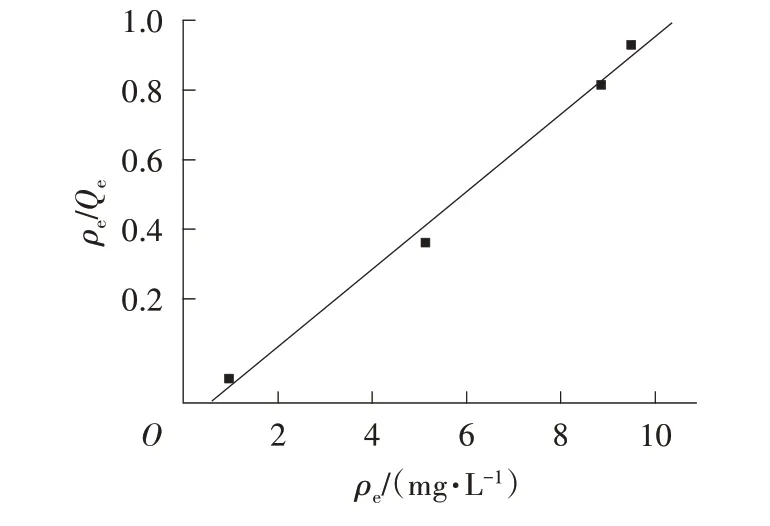
图10 LaNi0.95Fe0.05O3对甲基橙的吸附等温线

由表1 可知，2 种模型均具有较好的拟合效果（R2＞0.96）；根据2 种模型的相关系数可以看出，Langmuir模型能更好地模拟LaNi0.95Fe0.05O3对甲基橙的吸附热力学过程。

2.4 吸附动力学

图11 分别显示了准一级方程、准二级方程、Elovich 方程及颗粒内扩散方程拟合曲线，相关模型参数列于表2。由表2可以看出，准二级方程的相关系数R2=0.994 01，大于准一级方程的0.986 82，因此，准二级方程能更好地描述吸附剂对甲基橙的吸附过程。此外，Elovich 方程和颗粒内扩散方程的相关系数均大于0.99，表明LaNi0.95Fe0.05O3粒子对甲基橙的吸附可能存在2 种机理。首先，粒子表面的高粗糙度使得粒子表面不均匀，而Elovich 方程能更好地描述非均匀表面的吸附行为；其次，粒子的不规则性使粒子团聚时可能存在孔隙。因此，吸附过程可能由2 种扩散过程控制，第一阶段为液膜扩散，第二阶段为内扩散。

图11 动力学方程拟合曲线

表2 动力学模型及参数

3 结论

（1）制备了一系列镧镍铁氧体金属复合物，并对其结构进行表征，其中LaNi0.95Fe0.05O3对水中甲基橙具有良好的吸附效果，吸附速率快，且最大吸附量及去除率分别为0.940 mg/g 和91.85%，利用磁铁可以实现吸附剂与水体的快速分离，从而实现水中甲基橙的高效去除，回收后的吸附剂经10 mmol/L 盐酸溶液洗涤或400 ℃高温煅烧后可重复利用。

（2）等温吸附结果表明，25～70 ℃时，LaNi0.95Fe0.05O3对水中甲基橙的吸附率随着温度的升高而降低，表明该吸附是放热行为。Langmuir 等温线和Freundlich等温线模型拟合结果表明，Langmuir 等温线模型能够更好地描述LaNi0.95Fe0.05O3对水中甲基橙的吸附过程（相关系数R2＞0.99）。

（3）动力学拟合结果表明，准二级速率方程能更好地描述吸附行为；Elovich 方程和颗粒内扩散方程的拟合结果表明，由于粒子表面存在较大的不均匀性，吸附受液膜扩散和内扩散两个过程控制。