基于理想值的不确定机会约束最大满意度建模研究
张 露,巩在武,周 祎
(1.南京信息工程大学 管理工程学院, 南京 210044)
多属性决策是依据方案所具备的多种属性,在相对有限的方案中,分别进行排序和择优选择,已广泛应用于在经济、教育、军事等诸多领域中,是重要决策形式之一.属性值是区间数形式的研究已经十分丰富,随着大数据时代的到来,决策时能够掌握的数据量越来越大,对服从或近似服从正态分布属性值(如大群体的公众评价[1]、顾客需求[2])的多属性决策问题也逐渐兴起,对于服从正态分布属性值的处理方式学者们有着不同的方法,例如,在大规模群体决策中采用DEMATEL矩阵的聚类方法进行分组,运用三维区间密度算子对DEMATEL评分进行集结确定权重[3];或者利用3σ原则将属性值(正态分布)转化为区间数形式,然后利用可能度对各备选方案进行比较和排序[4];另外还有利用蒙特卡洛仿真的方法计算可能度,进而对备选方案进行比较和排序[5].上述研究大多数仍然建立在区间数多属性的决策思想之上.不少学者为了探寻属性值为具有正态随机分布特征的变量,提出了可能度这一概念,以实现变量之间可以相互比较[6],而后在前景理论的指导下利用正态分布的分布函数表示属性值的分布规律,计算出前景值进行方案排序[7-8].也有将传统的均匀分布二元语义标度进行改进,解决了二元语义不可比较的问题[9].随着决策环境不确定性的不断增加,当变量既不表现出随机特征也不表现出模糊特征时,文献[10]提出了不确定理论的新概念,属性值服从正态不确定分布多属性决策问题是研究的新课题.现有的多属性决策方法研究中,基于理想解的多属性决策方法,已经在方案属性值为区间数[11-12]、模糊数[13]以及不确定语言[14]等领域取得广泛的进展.文献[15]把理想值与满意度相结合,得到了属性值为实数条件下的最大满意度模型的多属性决策方法.文中尝试将基于理想值的最大满意度思想应用到随机变量和不确定变量多属性决策研究中,通过构建机会约束规划模型及其确定型等价类来获得决策问题的优化解.
1 问题描述
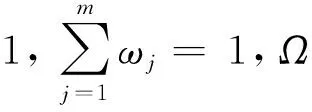
2 决策方法和步骤
以方案满意度为模型构建基础,在已知部分权重信息的情况下利用多属性决策方法首先构建出两个单一目标优化模型求解综合属性的正、负理想值,并给出各备选方案的满意度定义,构建了最大满意度的多目标优化模型[15].此方法可以推广到随机变量和不确定变量,但由于变量不同于干脆数,无法直接将属性值带入此模型,会对求解造成困难,文中将引入此满意度模型,设计一种更简便的,带有机会约束的随机规划和不确定规划模型,并通过将机会约束转化为确定性等价类的方法进行求解.
2.1 计算备选方案综合属性值的正、负理想值
已知部分权重信息,以期该方案的综合属性值最大的原理,构建出单目标优化模型,分别对各备选方案的正理想值和负理想值进行求解,由于研究中属性值服从正态分布,在整个求解过程中,将各属性值的期望值加入模型分别求解,得出各备选方案的正负理想值.

(1)

(2)
2.2 建立带有机会约束的最大满意度模型
在解决正态随机多属性的决策问题时,采取直接区间化的处理方式,就会导致区间内可能存在的变化趋势被忽略掉,为此将机会约束引入到基于方案满意度的多属性决策模型中,通过设定希望达到约束条件的置信水平(在不确定理论中,也称之为信度),在最大满意度的目标下求解出最优权重.从而建立方案属性值分别为正态随机变量和正态不确定变量两个带有机会约束的不确定单目标优化模型.
当方案属性值rij为正态随机变量时,建立单目标优化模型:
(3)
当方案属性值rij服从正态不确定分布时,建立单目标优化模型:
(4)
式(3、4)旨在解决已知部分权重信息的情况下,所有备选方案的满意度不小于某一阈值λi的概率大于等于预先给定的置信水平α的情况下求取λ的最大和,允许当一些不利的情况下,方案的满意度无法达到设定的数值,但其发生的概率要进行限定.
2.3 模型等价类转换计算属性权重
优化单目标优化模型式(3、4)中的约束条件是非线性的,且在研究中只讨论属性值均服从正态分布的情况,因此采取转化为确定性等价类的方法进行求解.
2.3.1 变量呈正态随机分布
定理1:首先考虑方案属性值呈正态随机变量特征,可以将模型式(3)中带有机会约束的约束条件转化为确定性等价类,因此可以将带有机会约束的不确定性模型转化为确定性线性目标规划模型:
(5)
2.3.2 变量呈正态不确定分布
定理2:当变量既不表现出随机特征也不表现出模糊特征时,考虑方案属性值服从正态不确定分布,可以将模型式(4)中带有机会约束的约束条件转化为确定性等价类,因此可以将带有机会约束的不确定性模型转化为如下确定性线性目标规划模型:
(6)
转化成确定性等价类后,通过对该模型进行求解,可以得出各备选方案的属性权重.
2.4 计算备选方案的综合属性值并进行排序

计算出各备选方案的综合属性值之后,按照首先对各方案综合属性值的均值大小进行排序,均值越大的备选方案往往越优,若出现均值相等的情况,需要对其方差进行比较,方差越小的备选方案越优,如若两个备选方案综合属性值的均值和方差均相等,则判定这两个方案排序结果相同的规则[5]对所有的备选方案进行排序.
3 算例
假设某所大学要对其学院展开评估,设该大学有4个学院(方案)(x1,x2,x3,x4),每个学院涉及的评价指标有3个属性(c1,c2,c3),分别是教学c1、科研c2和服务c3.并假定各属性的权重部分已知,即0.2≤ω1≤0.5,0.1≤ω2≤0.45,0.25≤ω3≤0.6.决策者针对每一个方案所对应的属性值所给出的评价结果均服从正态分布,规范化处理后的决策矩阵R(表1).试对4个学院的综合评估结果进行排名.

表1 规范化决策矩阵R
首先通过单目标优化模型式(1、2)求出综合属性值的正负理想值.此处的方案属性值用均值带入,求得各备选方案的理想值及其对应的权重向量(表2、3).
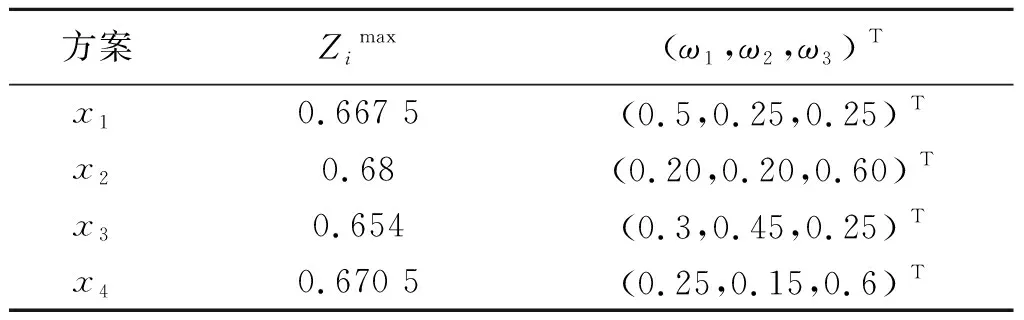
表2 备选方案综合属性值的正理想值
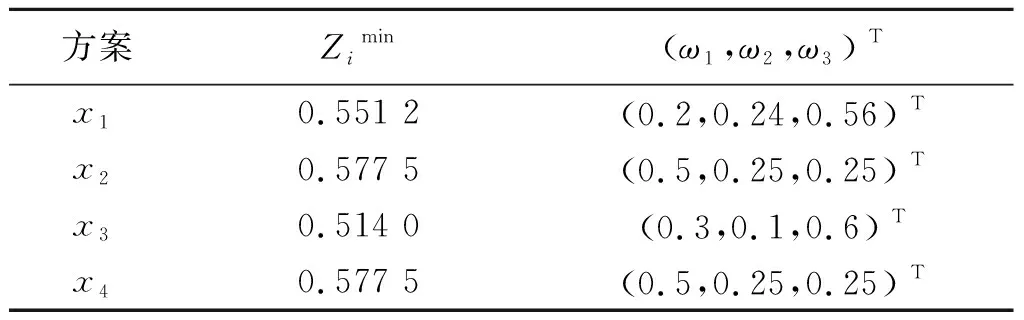
表3 备选方案综合属性值的负理想值
求得各方案综合属性值的正、负理想值之后,建立起文中所需的决策模型,同时完成机会约束向等价类的转化过程,然后求解各属性的权重.此处考虑两种情况,分别是方案属性值呈正态随机变量特征的正态不确定变量特征,分别求解出属性权重(表4、5).

表4 方案属性值呈正态随机变量时,属性权重计算结果

表5 方案属性值呈正态不确定变量时,属性权重计算结果
最后通过加权求和得出各个备选方案的综合属性值,并按照正态随机变量的比较规则对各方案进行排序.当属性值呈正态随机变量时,可得各方案的排序结果为x2≻x4≻x3≻x1,最优备选方案为方案2(表6);当属性值呈正态不确定变量时,可得各方案的排序结果为x2≻x4≻x3≻x1,最优备选方案为方案2(表7).

表6 方案属性值呈正态随机变量时,综合属性值Gi

表7 方案属性值呈正态不确定变量时,综合属性值Gi
4 结论
(1) 相较于现有的研究,充分利用了属性值服从正态分布这一特点,通过引入满意度概念,构建了带有机会约束的模型,通过将机会约束转化为确定性等价类的形式来获取属性权重,有效避免了专家决策过程中的主观影响,同时也避免了将正态分布转化为区间数进行决策所带来的失真问题.
(2) 研究未分析参数的设置对最优解获得的影响,进一步研究可以引入目标规划,允许部分方案不满足约束条件时获得最优解,达到较高的信度.

