展开过程：彰显运算教学的价值

【摘要】运算能力是个体数学素养的组成部分。基于发展数学运算素养的要求，教师在教学中不应仅仅满足于学生能够“正确、合理简洁”地进行运算，还应充分展开教学过程，彰显运算教学的“过程价值”。教学实施过程中需要关注估算与精算的融合，已知向未知的迁移，直观向抽象的过渡，具体向一般的跃升以及抽象回归具体的演绎。

【关键词】教学过程；运算能力；素养；直观；抽象

【中图分类号】G623.5【文献标志码】A【文章编号】1005-6009（2022）33-0055-03

【作者简介】侯红梅，南京市六合区马鞍学校（南京，211500）教师，一级教师。

运算能力是个体重要的数学能力之一，运算能力作为小学数学课程内容的核心，不仅要求“正确运算”，也要突出“合理简洁”地运算。在发展学生核心素养的背景下，需要进一步认识和优化运算教学过程，彰显教学的价值。

估算能力是个体在具体情境中，能够根据解决问题的需要，借助比较、判断、推理等认知过程，获得概略化结果的能力。教师在教学中应该意识到估算能力与精算能力是运算能力的两种不同形式，重视两种形式的协同配合，激活儿童不同的脑部区域，促进学生的全面发展。

苏教版三年级下册“两位数乘两位数”的笔算第一课时是乘法的精算教学，主要引导学生能够学会并运用两位数乘两位数（不进位）的运算方法。教材创设的情境是：幼儿园购进 12箱迷你南瓜，每箱24个。一共有多少个？这是一个精算的问题，通常学生不太会进行估算。因此，在教学时教师可以先提出估算的要求，引导学生估算一下大约有多少个。这样做一方面是增强学生估算的意识，另一方面也可以使估算为检验精算的结果服务。有的学生联系近似数的知识，能容易地估算出结果大约是200个；也有的学生能联系口算的方法，想到10×24= 240（个），12大于10，所以比240个多。有了估算的过程，当学生尝试用竖式计算出结果之后，可以反过来和估算的结果进行比较，体会估算可以得到概略化的计算结果。当然，在解决实际问题的练习中也应该逐步引导学生有意识地先估算，再精算。

数学知识是一个纵横联系的知识体系。在学习两位数乘两位数的笔算之前，学生已经学习过两、三位数乘一位数的笔算和两位数乘十以及整十数相乘的口算。教学时应该重视引导学生自主探索，让学生从已知逐步走向未知。

在学生探索24×12的计算方法时，教师要鼓励学生观察如下的情境图，思考可以怎样算出结果，并与同学交流。

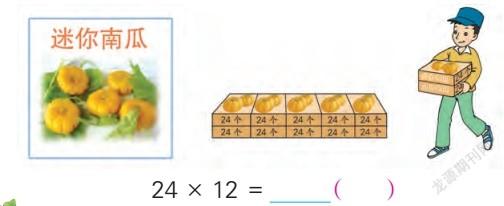
学生借助直观可能想到：6个2箱是12箱，先算2箱有24×2=48（个），再算6个2箱有48×6= 288（个）；也可能想到12箱可以分成10箱和2箱，先算10箱有24×10=240（个），再算2箱有24×2=48（个），最后算出12箱有240+48=288（个）。当然，学生还可能把24个作类似的拆分。教学时不能仅仅满足于学生运用已有的知识经验探索出运算结果，还要重视引导学生对这些方法进行分析、比较，从而提取出对新的运算方法有价值的经验。学生通过比较能够体会到，这些运算方法都是将新知转化成已知：可以把一个数拆成两个一位数相乘，再和另一个数连乘；也可以把一个数根据其组成拆成几个十和几个一，再分别和另一个数相乘。上述两种不同的拆分方法，在获得24×12的结果时无所谓优劣，但是分析、比较的过程孕伏了乘法的结合律和乘法对加法的分配律。以此为基础，教师可以出示新的问题：如果是13箱迷你南瓜，一共有多少个呢？学生自然会延续先前的拆分方法，通过交流发现没有学生把其中的13拆成两个一位数相乘，只能拆成10加3。由此引导学生体会到：两个两位数相乘并不总是可以拆成一个两位数连续乘两个一位数，但总可以拆成几十加几，再分别去乘。在此基础上，启发学生思考，能不能在竖式中进行计算呢？这就自然地引导学生从已知走向未知，体会数学规则的合理性。

学生学习运算的过程也是感悟抽象思想的过程。这里的抽象表现在：从运算的对象来看，先是对具体数量的运算，逐步过渡到数的运算；从运算方法的学习来看，先是直观的表征算法，逐步过渡到形式化的算法。教学时应注意引导学生经历抽象的过程，理解数学知识和方法的本质。

在学生尝试用竖式计算24×12之后，教师可以结合学生尝试的计算过程，引导学生理解关于具体数量的运算过程：第一步2乘24算出的是什么？第二步算的是几乘24？算出的是什么？最后一步算出的是什么？形成如下板书：

为了突出第二步算出的是10箱的个数，在这个阶段的竖式中仍然写出实际运算的结果240。

为了引导学生经历由具体数量的运算抽象到数的运算的过程，教学时可以穿插如下这个问题：24×12除了可以表示12箱迷你南瓜的总数量，还可以表示其他的问题吗？能不能举些例子？学生可能举出类似的实例：团体操表演时有12组，每组有24人，一共有多少人？一箱矿泉水有24瓶，12箱一共有多少瓶？等等。这样，学生就可能感悟24×12能够表示很多具体的问题，具有一般性。

在此基础上，引导学生在一般的数的意义下讨论形式化的算法。教师可以提出问题：如果用24个点表示24，24×12怎样表示？引导学生构造点阵图，并思考在竖式计算时每一步算的是什么，将竖式计算的过程与直观的点阵图联系起来，形成如下板书：

此时，再引导学生思考竖式中哪里可以简化，得出简便的竖式写法。

在学生初步学习两位数乘两位数的计算方法之后，可以让学生先完成“想想做做”第1题，以熟悉刚刚学会的两位数乘两位数竖式计算的操作程序。这时需要提醒学生思考每一步算出的是什么，让学生将运算的几个步骤连贯起来，独立地进行计算，从而逐步内化算法。

教学时应注意两个问题：一是引导学生比较例题和后面的3道算式，说说今天学习的是怎样的计算，顺势解释课题；二是引导学生比较竖式计算的过程，说说两位数乘两位数应该怎样计算。第一个问题相对比较容易，但是以这样的方式揭示课题，更便于学生在头脑中留下深刻的印象，也体现了课题本身表达的学习内容的一般性。第二个问题对于学生而言往往是学习的难点，很多学生对具体算式的计算方法是清楚的，但是无法从更一般的高度对运算方法进行总结概括。教师可以提示学生用“先算……再算……最后算……”的方式表述运算方法，逐步提高语言概括和表达能力。缺失概括的过程，算法永远都是具体化的，无法上升到一般。当然，算法的形成过程随着运算的对象逐步变化，也存在逐步完善甚至更新的过程。

运算教学既要让学生掌握正确运算的方法，还要通过现实情境的应用感悟运算方法学习的意义，并在解决问题的过程中学会合理灵活地进行运算。

这一阶段的应用也可以分为两个层次：一是在应用中进一步内化算理。教材“想想做做”第2题就是这样的实际问题：

这里最容易出现错误的是运算过程的第二步，它表示买20个热水瓶的总价。学生联系具体情境更容易理解這一步的运算意义。

二是在解决问题的过程中内化算法。教材“想想做做”最后一题就是这样的问题：

学生可以先通过估算解决问题，再利用精算得到问题的答案，这样就使得学生在解决问题的过程中体会到学习的价值。以此为基础，教师改变情境中的某一个数，如此，新的问题在应用中自然生成了，成为伴随学生自主探索的新的动力源泉。

学生在运算过程中可能会随时出现各种错误，这是正常的。教师要重视让学生养成验算的习惯，有错误及时改正，培养严谨的学习态度，这也是运算教学过程价值的重要组成部分。