基于灰色理论的电力监控数据多因素预测模型∗

樊锐轶 高 志 曹海门 王梦嘉

(1.国网河北省电力有限公司，河北 石家庄 050000；2.国网石家庄供电公司，河北 石家庄 050000)

电力数据监控是电力管理部门进行电力调度、用电、计划、规划必须完成的重要工作之一。其中，负荷预测又是用电市场进行用电计划管理的必要基础[1－4]。实质上，负荷预测即为建立预测数学模型，描述电力负荷发展规律。随着大数据技术的发展，大数据技术被广泛应用在电力负荷预测上，大数据技术的应用前提是需要海量的相关数据，对数据量要求较高。但很多领域可以用于预测的样本数据通常较少[5－6]。适合分析处理缺少样本信息数据的灰色系统理论可以弥补大数据此方面的缺陷，这为电力负荷预测提供了有效分析手段[7]。

目前广泛应用的单变量GM(1，1)作为最常用的灰色预测模型，其要求样本数据少、运算方便、原理简单[8]，但GM(1，1)同其他预测模型一样，存在其局限性，在实际工程应用中会受到一定限制。因此，一些学者提出了基于GM(1，1)改进的算法，如干涉因子灰色预测模型、新信息灰色模型以及新陈代谢灰色模型等，上述优化模型在不同的使用工况中对传统GM(1，1)预测模型进行了一定程度的改进。但其仍为单因素预测模型，且预测精度仍不够理想[9－14]。

基于电力监控数据分析建模的研究现状，本文采用基于有限电力监控数据的多因素GM(1，1)优化模型，分析了10 年的社会用电结构，以不同结构的用电量数据为基础，建立并检验了基于电力数据多因素的灰色预测模型。全社会不同结构电力负荷预测结果表明，该模型预测最大误差小于4.8%，结果证明了该模型的有效性和可用性。上述研究对于丰富电力负荷预测手段，弥补大数据需求数据量较高的局限性均具有十分重要的现实意义。

1 基于有限电力监控数据的多因素预测GM(1，1)建模方法

1.1 灰色理论在电力系统应用中的提出

随着大数据技术的发展，大数据技术被广泛应用在电力系统当中，基于大数据的方法可以为负荷，主变线路负载，电压质量，设备运行风险等预测与评价提供解决方案。但传统的大数据技术在应用中存在以下问题:

(1)根据大数据的基本理论要求，精确预测的前提是拥有全面大量而又准确的样本数据，但实际中，很多地区可以用于预测的样本数据量无法满足要求。

(2)即使数据量满足要求，但电力系统大数据种类庞杂、横跨专业多等特点导致数据质量不高，这也成为大数据方案应用误差来源的主要原因。

基于以上大数据应用的现状，适合分析、处理缺少样本信息数据的灰色系统理论可以用于负荷，主变线路负载，电压质量，设备运行风险等的预测与评价[13－14]。本文提出了基于有限电力监控数据的多因素预测GM(1，1)模型，以负荷预测为研究对象，探索作为补充大数据方案的灰色理论在电力系统中的应用。

1.2 GM(1，1)建模方法

本文提出的电力负荷预测的一般建模方法主要创新点在于基于有限电力监控数据的多因素负荷预测。建模方法如下:设电力系统负荷预测的建模数据选择n个建模因素(本文中n＝4)，建模数据分为h个时间段(本文中h＝10)。用于电力负荷预测建模的原始数据可表示为:

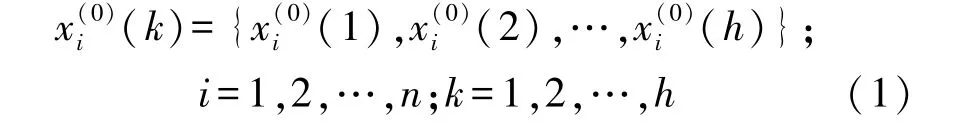
确定了数据初始序列后，基于有限电力数据的灰色预测的建模方法分为3 步骤，分别为累加运算，计算驱动因子和累减还原计算[4]。本文首先利用累加运算处理初始序列(k)，进一步根据公式(2)和(3)确定(k)的一阶累加序列(k)。

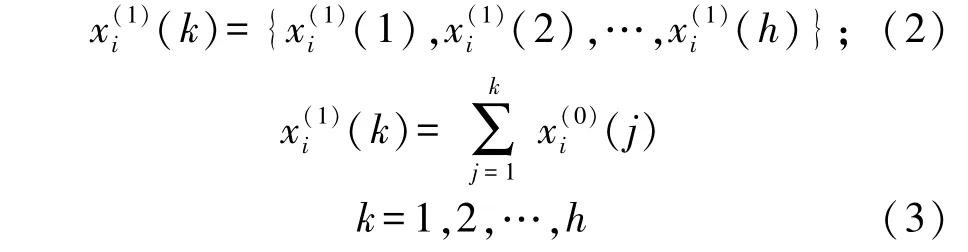
累加运算完成后，本文将不延用传统的计算方法。由于各个因素的用电负荷相互影响，因此建立n元的常微分方程组如公式(4)所示。

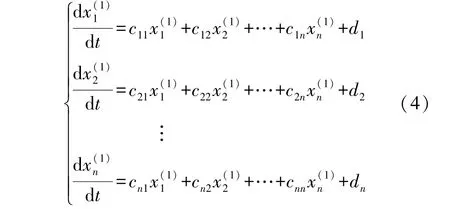
式(4)可以表示为矩阵形式，如公式(5)所示。

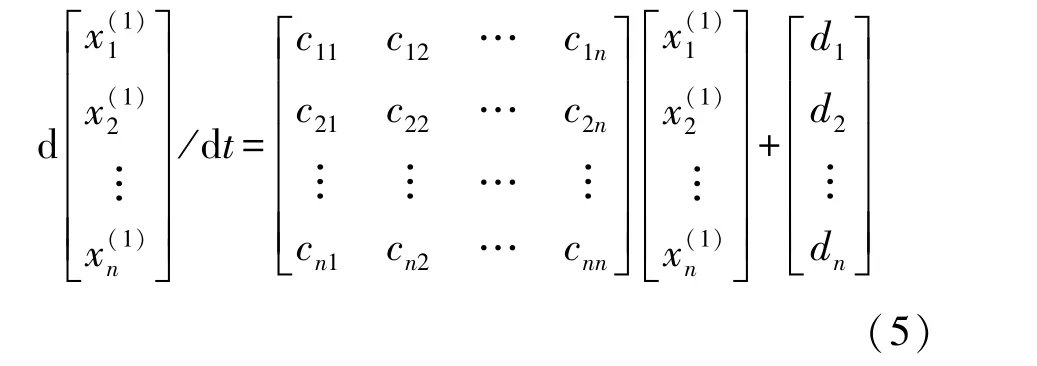
将公式(5)简化为公式(6)。

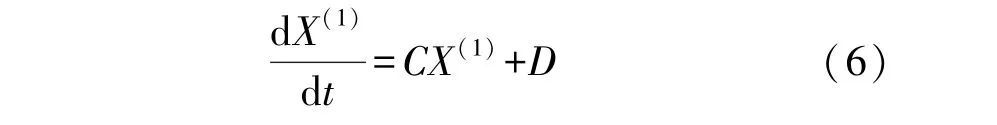
进一步，使用最小二乘法推导参数矩阵C，其中，在积分计算过程中，使用梯形近似公式。具体步骤如下:在区间[k－1，k]上对公式(4)进行积分，得公式(7)。

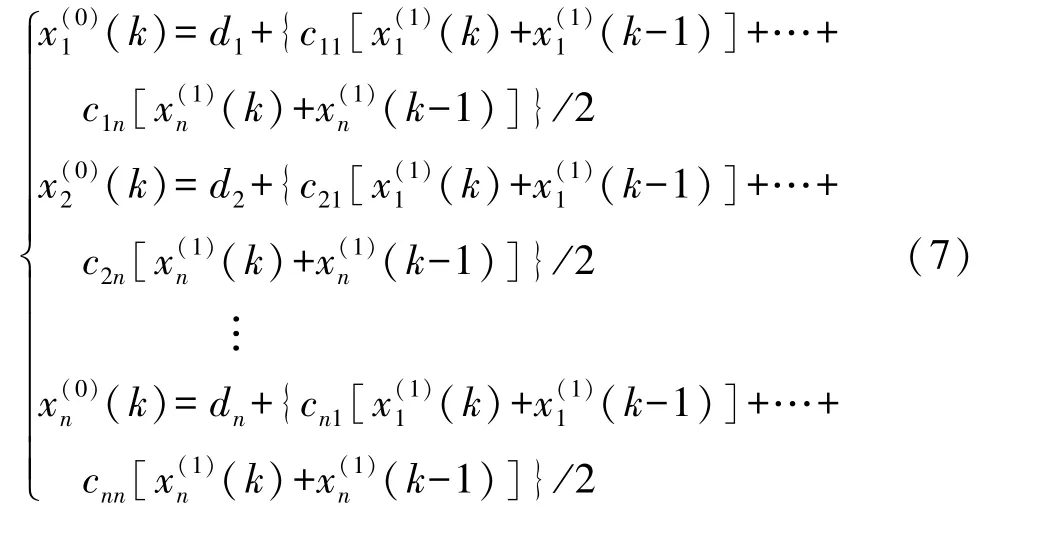
将公式(7)简写为公式(8)。

因此可以对公式(8)求取最小二乘解，进而得到参数的估计值如下。

最后，根据积分生成变换原理，公式(6)两边同时乘以e－At，再对所得公式进行区间[t1，t]上的积分。积分可得公式(10)。

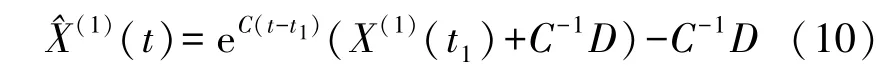
本文模型中令t1取值为1，进而通过公式(11)的累减运算，可得到多因素的电力负荷预测值。

2 基于有限电力数据的多因素分析预测

2.1 建模原始用电量数据分析

本文选取10 年的社会用电量作为建模数据，其中每年的用电量分为4 个组成部分，分别为第一产业用电量，第二产业用电量，第三产业用电量和城乡居民用电量。4 部分用电量即为4 因素的电力负荷预测。

从表1 中可以看出，不同产业的用电量增长趋势虽然几乎一致，但其增长速率却有所差异。例如，对于第一产业用电量，变化趋势并不呈现一直增长的状态。在第6 年及第8 年，其第一产业用电用量均发生下降的趋势。分别从810.4 亿千瓦时降低至802.4 亿千瓦时(第5 年～第6 年)和821.6亿千瓦时降低至810.4 亿千瓦时(第7 年～第8年)。

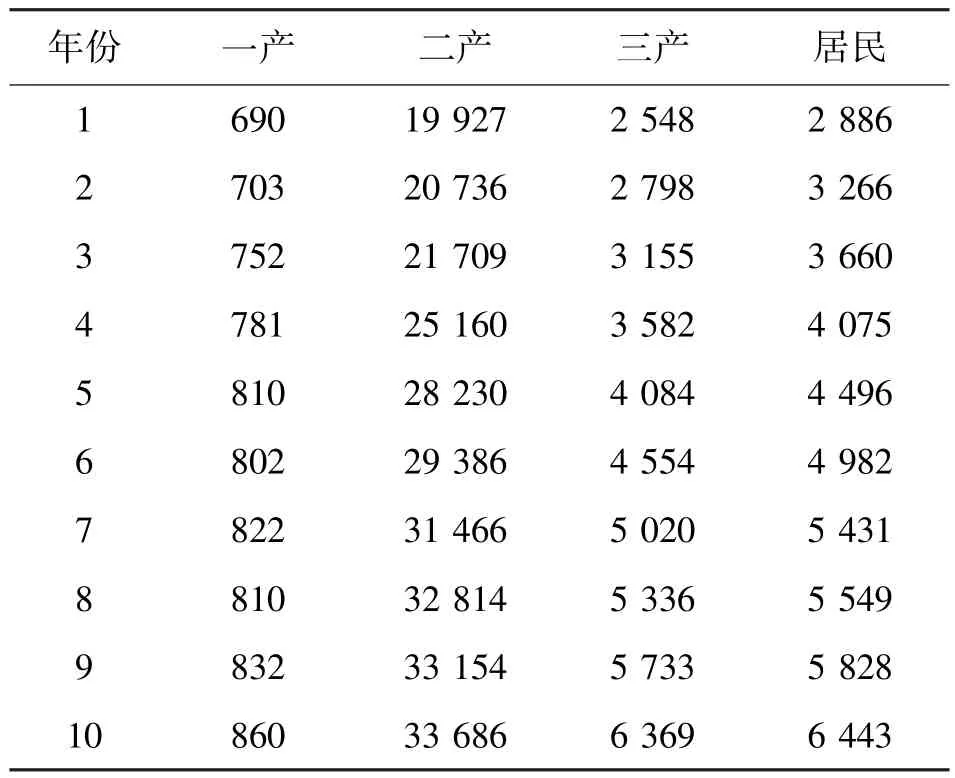
表1 全社会用电量 单位:kW·h

相反，对于第二产业，第三产业以及居民用电，随着年份的增加，用电量变化趋势一直处于增长状态。此外，用电量增长趋势并不是完全符合线性关系。

2.2 基于有限电力数据的多因素预测结果

综上所述，多因素的电力负荷预测模型十分必要。本小节根据第1.2 节所述多因素预测GM(1，1)建模方法对表1 的数据进行建模预测。

计算得到系数矩阵aij和bi分别为:

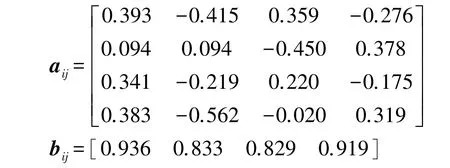
进一步，根据第1.2 节所述方法计算，可得多因素的用电负荷计算结果，第一产业用电量，第二产业用电量，第三产业用电量和城乡居民用电量计算结果与实际值的对比如图1 所示。

从图1 中可以看出:

图1 全社会用电量预测结果

(1)本文提出的基于电力数据多因素负荷预测模型可对第一产业，第二产业，第三产业及城乡居民用电的用电负荷同时进行计算，实现了多因素的用电负荷的预测。

(2)本模型对于四种用电结果的预测都较为符合实际用电趋势，虽然存在小范围的误差，但是整体上预测结果较为理想。

(3)本模型实现了基于有限电力数据的负荷预测，弥补传统大数据技术在负荷预测方面需求数据量较高的局限性。

2.3 多因素电力监控数据预测误差

为分析本模型预测误差，本节进一步计算其每个预测数据点的预测相对误差。计算结果如图2 所示。从图中可以看出:预测相对误差的最大值出现在第2 年的第二产业。本文提出的多因素电力负荷预测模型的最大误相对误差小于4.8%，此外，大部分误差在3%以下，预测精度较高。可为电力系统的管理提供负荷预测的指导。

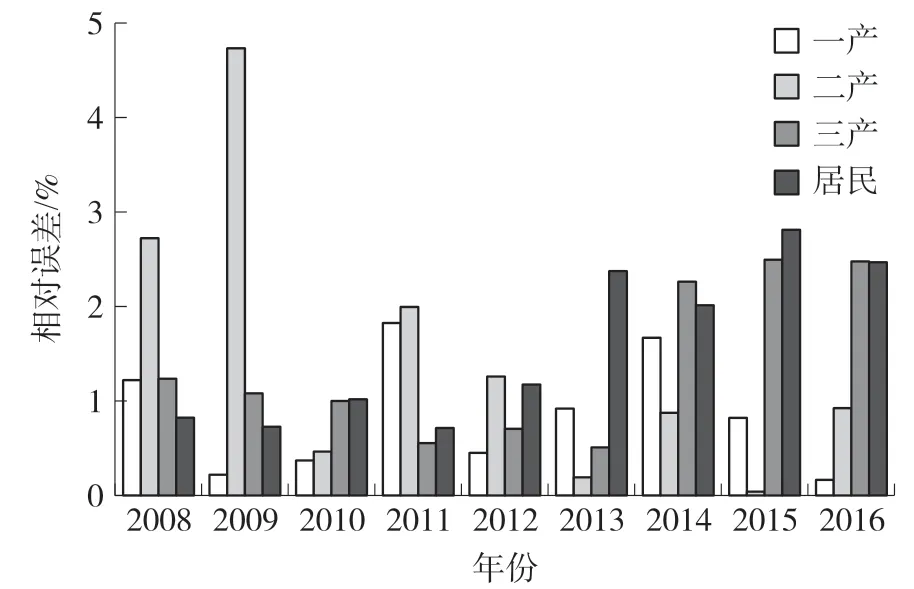
图2 全社会用电量预测误差

3 结论

本文提出基于有限电力数据多因素的GM(1，1)优化模型，分析了10 年的社会用电结构，通过不同结构的用电量数据，建立并检验了基于多因素的灰色电力监控数据预测模型。

本预测模型可对第一产业，第二产业，第三产业及城乡居民用电的用电负荷同时进行计算，实现了多因素的用电负荷预测。此外，本模型实现了基于有限电力监控数据的负荷预测，弥补传统大数据技术在负荷预测方面需求数据量较高的局限性。

全社会不同结构电力负荷预测结果表明，该模型预测最大误差小于4.8%，结果证明了该模型在预测电力监控数据方面的有效性和可用性。