一种有效的非线性电路及其特性的透明建模方法∗

陈和娟 房义军

(1.无锡商业职业技术学院汽车技术学院，江苏 无锡 214153；2.江苏大学农业工程学院，江苏 镇江 212013)

符号分析和符号建模的目标是得到模拟电路行为的可解释表达式[1－2]。符号分析通过电路的拓扑分析来提取表达式，而符号建模则通过采用SPICE仿真数据来提取表达式。这些表达式可应用于自动电路尺寸的分析模型生成、设计空间探索、包括统计分析、模拟故障诊断和可测试性分析在内的重复公式评估，以及仿真行为模型生成等[3]。更重要的是可以为设计人员提供对电路理解的工具，因为它有助于在电路尺寸、布局、验证和拓扑设计方面做出更好的决策。因此，生成符号表达式的方法备受关注。

尽管符号分析最先出现，但其主要缺点是局限于线性化和弱非线性电路。这只能通过分段线性/多项式建模方法来克服[4－5]，代价是失去透明性(可解释性)。

在建模中利用SPICE 仿真是可行的，因为仿真器可以很容易处理非线性电路、环境影响(如温度、电源电压、负载)、制造影响、不同工艺(如接近角)等。根据仿真数据，构建一个模型y＝f(x)，其中y通常是一个性能指标，x包括设计、工艺或环境变量，而f为SPICE 映射的近似值。通常采用的模型包括线性模型[6]、基于正项式的模型[7－8]和二次多项式模型[9－10]。在文献[7－8]中，尽管构建了基于正项式的符号模型，但存在的问题是模型被约束到一个预先定义的模板，从而限制了函数形式。此外，这些模型有许多项，限制了它们对设计者的可解释性。正项式可以拟合数据，但在模拟电路中并不能保证这一点；文献[9－10]研究了二次多项式模型构建，但二次多项式也存在限制性结构。

也有学者提出采用样条函数[11]、多元自适应回归样条函数(Multivariate Adaptive Regression Splines，MARS)[12]、前馈神经网络(Feedforward Neural Network，FNN)[13]、增强型前馈神经网络(Boosted-FNN，B-FNN)[14]、支持向量机(Support Vector Machines，SVM)[15]、最小二乘支持向量机(Least Squares-Support Vector Machines，LS-SVM)[16]

和克里格法(Kriging)[17]来构建符号模型。然而，这些模型要么遵循一个过度限制的功能模板(限制了它们的适用性)，要么是不透明的，因此无法为设计者提供观察和可解释性。

对此，本文提出了一种新的符号建模方法，本文将这种建模方法称为基于进化的规范函数形式表达式(Evolution Based Canonical Functional Form Expressions，EB-CFFE)。它采用SPICE 仿真数据为电路应用生成可解释的数学表达式，将电路性能与设计变量联系起来，能够为任意非线性电路及其特性生成具有更开放的函数形式的符号模型，同时确保模型是可解释的(透明的)。提出的符号建模最适合于有适当偏差的设计区域(即设计变量有较小的更改)，因为覆盖不正确偏差区域的模型对于手工检查来说太复杂了。

1 问题及背景知识

1.1 问题构建

本文研究的建模问题的输入与输出如下。

输入:(1)X和y:集合{xj，yj}(j＝1，…，N)为数据样本，其中xj为Nd维的设计点j，yj为从该设计的SPICE 仿真测得的对应的电路性能值。可采用实验设计或电路优化生成数据样本；(2)无模型模板。

输出:一组符号模型M，它给出最小模型复杂性f1和最小模型预测误差f2之间的帕累托最优权衡，这个约束最优化问题用公式表示为:

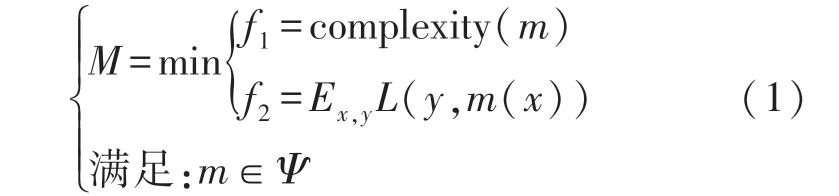
式中:Ψ为无模板符号模型空间。算法将遍历Ψ返回一个帕累托最优集合。每个模型m将一个Nd维的输入x映射到一个标量电路性能近似，即＝m(x)。复杂性定义为区分不同模型之间自由度的某种度量(见式(5))。Ex，y L是给定m对未来预测的预期损失，其中L为平方误差损失函数:

根据定义，帕累托最优集合M中没有哪个模型优于其他任何模型。在本文情形中，如果{fj(ma)≤fj(mb)}∀j且{fj(ma)(fj(mb)}∃j，j＝{1，2}，则模型ma优于另一个模型mb。也就是说，要达到帕累托最优，一个模型必须在两个目标上至少与任何模型一样好，在一个目标上优于任何模型。

1.2 背景知识—基因编程

基因编程(Genetic Programming，GP)[18]是一种进化算法，GP 个体(设计空间中的点)具有树的显著特征。由于符号模型是一个函数，可以表示为一颗树，所以对上述模型的搜索可以通过GP 搜索来完成。

标准GP 结果的函数形式是完全不受限制的，但不受限制的形式总是难以分析。GP－进化函数非常复杂且具有不可解释性。文献[18－19]表明GP－进化函数非常庞大且相当复杂，如果不与诸如Mathematica 这样的工具进行适当的交互，通常很难理解它们。

2 提出的EB-CFFE 建模方法

2.1 EB-CFFE 规范形式函数

EB-CFFE 设计遵循2 条准则:确保每个节点的最大可表达性，确保全部候选函数都是直接可解释的。图1 所示为EB-CFFE 函数的一般结构，尽管它可以无限地深入(进化)下去，但为了保持可解释性，它通常只能达到所显示的深度。它在乘积的和表达式与和的乘积表达式级别之间交替使用。每个乘积的和表达式是一个总的偏移项加上加权基函数的加权线性相加。一个基函数是乘积项的组合，其中每个乘积项是一个多项式/有理式、零或多个非线性运算符，以及零或多个单位运算符。每个乘积项充当通往下一个乘积的和的层的“门”。

图1 EB-CFFE 进化出的规范形式函数

图2 所示为一个示例函数及其对应的树。在函数的7.1/x3部分，7.1 是树的左上方w0，1/x3是其相邻的vars 的poly/rat'l。1.8 对应顶部的w1，x1是其相邻的vars 的poly/rat'l。函数的log 对应于nonlinear func，它在树中包含加权线性加(weighted linear add)项－。这一项本身已经中断:函数的－1.9 是树的较低的woffset，8.0/x1对应树的左下方w0×poly/rat'l of vars，对应于树的右下方的w1×poly/rat'l of vars。注意，EB-CFFE 只在需要系数的地方放置系数，而不在其他地方放置系数。

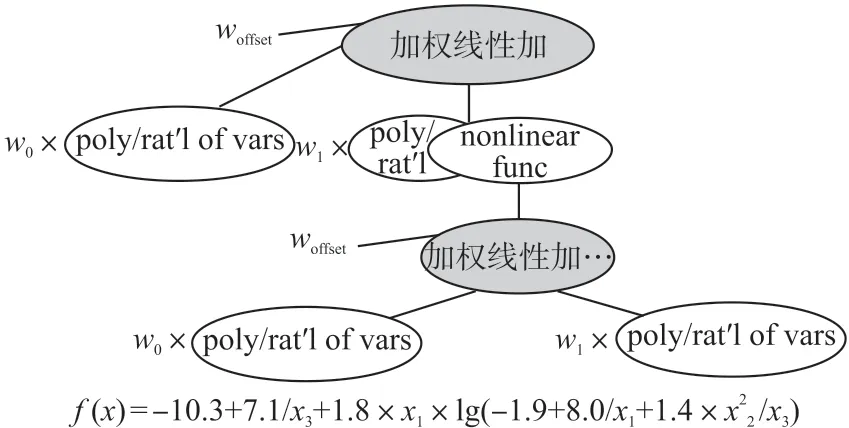
图2 采用文本形式的函数示例及相应的EB-CFFE 树形式

注意，不存在限制一个线性加层到下一层的非线性函数。EB-CFFE 的典型使用将限制乘积项层的数量仅为1 或2，因此确保不会出现非线性成分的过度混合，如lg(sin(exp(x)))。对基函数的最大数目也可能有一个限制。由于采用了规范形式，故所有进化函数都是直接可解释的，不需要符号处理。

2.2 EB-CFFE 搜索算法

本节描述EB-CFFE 函数中采用的搜索算法。EB-CFFE 搜索采用GP 作为起点，但为了正确处理无模板符号建模，本文对GP 进行扩展。主要通过2种方式解决复杂性和可解释性问题:一是多目标方法，它在误差和复杂性之间提供权衡；二是专门设计的语法和操作符，用于将搜索限制到特定的函数形式，而不会排除期望的解。在EB-CFFE 中，总的表达式是NB个基函数Bi的线性函数，i＝1，2，…，NB:

一个EB-CFFE 个体m有一个GP 树来确定每个基函数m＝{B1，B2，…，BNB}。线性系数a∈RNB＋1是在最小二乘成本函数式(2)上采用线性回归实时确定的。

2.2.1 多目标方法

EB-CFFE 采用最先进的多目标进化算法，返回一组个体，它们共同权衡模型误差和复杂性，即式(1)中的目标f2和f1。误差(预期损失Ex，y L)通过训练误差εtr来近似，εtr为训练数据上的个体m的归一化均方根误差:

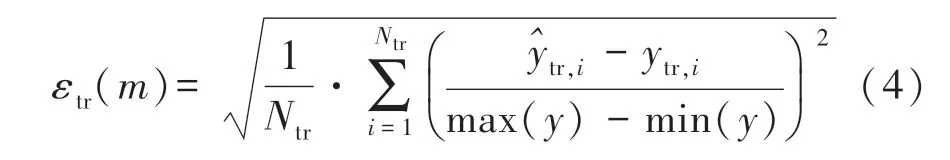
式中:Ntr为训练样本数，ytr，i为训练输出ytr的样本i，＝F(xtr，i；m)，xtr，i为训练输入Xtr的样本i。注意，y值被y缩放，而不是ytr；测试误差εtest有类似的公式，只是将Ntr个训练点{ytr，Xtr}用Ntest个测试点{ytest，Xtest}替换。

复杂性由基函数数目、每棵树中的节点数以及变量组合(Variable Combos，VCs) 的指数来度量，即:

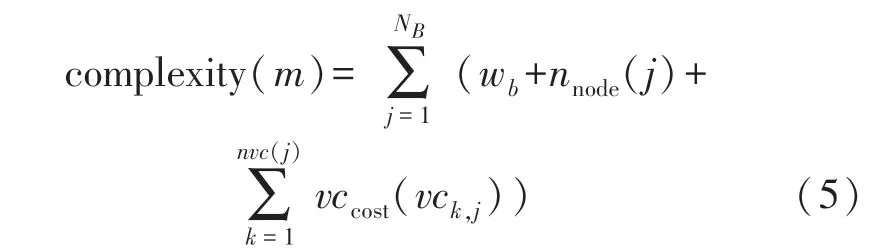
式中:wb为给定每个基函数最小成本的常数，nnode(j)为基函数j的树节点数目，nvc(j)为基函数j的VCs的数目，具有成本:

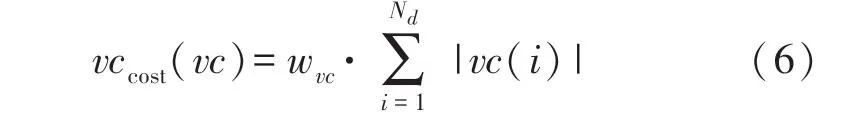
方法在生成过程中通过保持向更低复杂性的进化压力来实现简化，从而可以避免在误差或复杂性上作出预先决定，因为算法生成一组模型来提供各种备选方案的权衡，而不是只生成一个模型。

2.2.2 规范形式函数的语法实现

在GP 中，一种限制搜索的方法是通过语法[20]。基于树的进化算子(如交叉和变异)必须遵循语法的派生规则。

尽管语法可以有效地约束搜索，但目前还没有针对函数形式进行设计的语法。在设计这样的语法时，允许所有的函数组合(即使仅用一种规范形式)是很重要的。

表1 所示的EB-CFFE 语法是为创建线性和非线性函数的单独层而设计的，并按照图1 放置系数和变量。

表1 EB-CFFE 语法

首先解释表1 中的记号。粗体表示非终结符号，非粗体表示终结符号。每一行(或两行)显示了左边的非终结符号可以映射到(｜→)的可能表达式。可能表达式即派生规则用OR 操作符“｜”分隔。

其次来解释语法是如何实现规范形式函数的。REP 是“重复(repeating)”的缩写，如“重复操作符”REPOP(REP operators)和“重复变量组合”REPVC(REP variable combo)，在后面还有进一步说明。开始符号为REPVC，它扩展到一个基函数(一个个体有几个根级基函数)。注意操作符之间的明显区别。根是变量(REPVC)和/或非线性函数(REPOP) 的乘积。在每个非线性函数内是REPADD，即下一级基函数的加权和。

VC 为变量组合(Variable Combo，VC)，旨在保持多项式/有理式的紧凑表示。它的扩展可以直接在语法中实现；尽管在本文的基本系统中存储了一个向量，以保存每个设计变量的整数值作为变量的指数。如示例向量[1，0，－2，1]，它意味着(x1×x4)/(x3)2，并且根据式(6)，有成本｜1｜＋｜0｜＋｜－2｜＋｜1｜＝4。这种方法保证了紧凑性，并允许对向量使用特殊操作符。

在确定系数值时，要区分线性系数和非线性系数。如前所述，EB-CFFE 个体是一组线性相加的基函数。每个基函数是一棵语法派生的树。线性系数是通过对所有输入样本的每棵树进行计算得到一个基函数输出矩阵来找到的，然后对该矩阵和目标输出向量应用最小二乘回归来找到最佳线性权值。

对于树中的每个非线性系数W(即不能通过线性回归找到的系数)，附带一个实数值，其值在范围[－2×B，＋2×B]。在树的解释过程中，值被转换成[－1×10B，－1×10－B]∪[0.0]∪[1×10－B，1×10B]，B为用户集。

POW(a，b)表示ab。当符号2ARGS 扩展到包含MAYBEW 时，底数或指数(但不能都是)可以是常数。

设计者可以关闭表1 语法中的任何规则，如果考虑不想要或不需要。例如，可以很容易将搜索限制在多项式或有理式，或者删除可能难以解释的函数，如sin 和cos。还可以改变或扩展操作符或输入，例如，包括Wi、Li和Wi/Li。

2.2.3 增强EB-CFFE 算法

算法1 所示为ExtractSymbolicCaffeineModels()算法实现的伪代码。它接受训练输入X和训练输出y，将输出一组帕累托最优模型M。第1 行将M、当前的父元素P集合和当前的子元素Q集合初始化为空集合。第2～3 行循环遍历种群大小Npop，从可能的规范形式函数ψ空间中随机抽取每个个体Pi。第4 行开始第5 行和第6 行的进化算法(Evolutionary Algorithm，EA)的代循环。当达到目标代数Ngen，max时，终止循环。第5 行执行主要的EA 工作。第6 行更新帕累托最优个体M的外部存档，通过对现有的M进行过滤，其中最近更新过M的父结点P和子结点Q。第7 行结束ExtractSymbolicCaffeine-Models()运行，返回帕累托最优符号模型M。

算法1 ExtractSymbolicCaffeineModels()步骤伪代码

2.2.4 进化搜索算子

现在描述树是如何随机生成的，并解释树上的搜索算子。搜索算子按其搜索表示分组为:语法、实值系数、变量组合(VCs)和基函数。

从给定符号随机生成树和子树只需要随机选择其中一个符号的一个派生，并递归地生成(子)树，直至遇到终结符号。

对树的语法限制得到遵循自然语法的交叉算子和突变算子。算子工作如下:它随机选择第一个父节点上的一个节点，然后随机选择第二个父节点上的一个节点，约束条件是它必须与第一个节点具有相同的语法符号(如REPOP)，最后交换对应于每个节点的子树。突变包括随机选择一个节点，然后用随机生成的一个子树替换它的子树。

VCs 的特定结构得到合适的算子，包括一点交叉和对指数值的随机加或减。

每个个体有一个基函数列表，这也得到特定的算子:通过从两个父节点之一随机选择大于0 的基函数创建一个新的个体，删除一个随机基函数，添加随机生成的树作为基函数，从一个个体复制子树，为另一个个体创建一个新的基函数。

3 实验及分析

本节给出EB-CFFE 应用于模拟电路建立符号模型，将设计变量映射到性能，解决有13 个输入变量的问题，从而表明所生成的实际符号模型、测试误差与复杂性之间的权衡、预测误差和复杂性与其他主流建模方法的比较。

3.1 实验设置

x1＋x2、x1×x2、max(x1，x2)、min(x1，x2)、power(x1，x2)和x1/x2；条件运算符包括≤(testExpr、condExpr、exprIfLessT hanCond、elseExpr) 和≤(testExpr、0、exprIfLessT hanCond、elseExpr)；任意输入变量都可以在{…，－1，1，2，…}内有一个指数。

实例中所建模的电路为一个高速CMOS 跨导运算放大器(Operational Transconductance Amplifier，OTA)，如图3 所示。目标是找到低频增益(ALF)、单位增益频率(FU)、相位裕量(PM)、输入参考偏置电压(VOFF)和正、负转换速率(SRp，SRn)这6 个性能指标的表达式。为了直接与正项式方法进行比较，输入和输出都不缩放，只是FU为对数缩放，因此均方误差计算和线性学习会偏向于FU的高幅值样本。

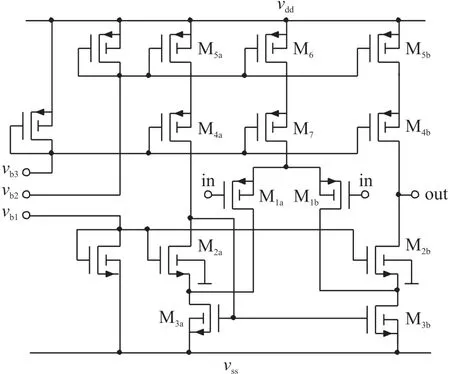
图3 CMOS 高速OTA

采用工作点驱动[21]，其中电流和晶体管栅驱动电压构成了设计变量(在本实例中有13 个变量)。设计点按比例dx＝0.1(其中dx为变量值与中心值的%变化)得到243 个样本。未经过滤的样本用作训练数据输入。测试数据输入也采用243 个样本，但dx＝0.03。

运行设置:基函数的最大数目NB＝15，种群大小Npop＝200，代数目Ngen，max＝5000(有足够的时间来收敛)，最大树深度＝8(使得每个基函数恰好有一个层的非线性运算符)，W系数范围为[－1×1010，－1×10－10]∪[0.0]∪[1×10－10，1×1010](即B＝10，因此，系数可以涵盖20 个数量级，包括正、负)。所有运算符都有相同的概率，除了参数突变的可能性是5 倍(为调整紧凑函数)。复杂性度量设置为wb＝10，wvc＝0.25。

对训练数据和单独测试数据计算其归一化均方误差εtr和εtest，这是模型质量的标准度量。测试误差εtest最终是更重要的指标，因为它度量模型对不可见数据进行概括的能力。

3.2 实验结果

3.2.1 EB-CFFE 符号建模性能测试

首先测试由EB-CFFE 生成的一些符号模型，观察哪些符号模型具有<10%的训练和测试误差，且有最低的复杂度。表2 所示为得到的图3 的OTA的6 个性能指标的规范形式函数。可以看到，每个函数最多有4 个基函数，不包括常数。对于VOFF，常数就足以使误差保持在10%以内。还可看到，有理函数形式最多。在这些目标误差下，只在ALF中出现一个非线性函数ln()。

表2 图3 的OTA 的EB-CFFE 生成的符号模型

可以通过对这些方程的分析，来了解拓扑中的设计变量是如何影响性能的，以提供可解释性。例如，ALF与OTA 的差动对上的电流idl成反比，或者SRp仅依赖于id1和id2以及id1/id2的值，或者在采样的设计区域内，设计变量之间的非线性耦合非常弱，通常仅为同一晶体管变量的比值，或者每个表达式仅包含设计变量的一个子集，或者晶体管对M1和M2是唯一影响6 个性能指标中的5 个的器件。

图4 所示为OTA 的6 个性能指标对于训练误差εtr、测试误差εtest和基函数数目与复杂性之间EB-CFFE 生成的权衡。

可以看到，对于训练误差与复杂性的权衡中的全部模型随着复杂性的增加，训练误差减小。在每个性能指标中，EB-CFFE 会生成大约50 个不同模型的权衡。正如预期的那样，零复杂性模型(即常数)有最高的训练误差约为10%～25%，最高复杂性模型有最低的训练误差约为1%～3%；

对于复杂性与基函数数目之间的关系，由于复杂性是由基函数的数目和每个基函数内每棵树的复杂性构成的函数，所以在这些曲线中可以看到，基函数数目随着复杂性的增加而增加。但有时在现有的基函数中增加更多的树而不增加更多的基函数会增加复杂性。这可以从曲线中看出，随着复杂性的增加，基函数的数目可能趋于平稳。

从图4 还可看到，与训练误差不同，测试误差不是随着复杂性的增加而单调减小。这意味着一些不太复杂的模型比更复杂的模型更具预测性。

图4 OTA 的每个性能指标的符号模型的训练误差、测试误差和基函数数目与复杂性之间的关系

值得注意的是，在几乎所有情况下，测试误差都小于训练误差，表明了EB-CFFE 方法能为具有更多变量的电路提供表达式的潜力。

3.2.2 与正项式符号模型的比较

本节将本文的EB-CFFE 符号建模与正项式建模方法进行比较。首先比较模型的复杂性，比较的是正项式系数的数目与出现在EB-CFFE 表达式中的系数数目，结果如图5 所示。可以看到，EB-CFFE模型比正项式模型紧凑1.3 倍～6.4 倍；其次比较EB-CFFE 和正项式建模方法的预测能力，将训练误差固定来比较测试误差，结果如图6 所示。可以看到，在全部6 个性能指标中，EB-CFFE 模型有5 个优于正项式模型，仅在VOFF中，正项式模型比EB-CFFE略好，但EB-CFFE 模型比正项式模型要紧凑6.2 倍。

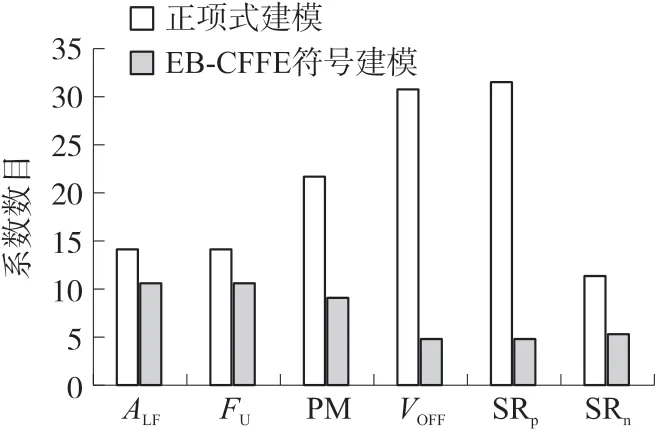
图5 EB-CFFE 模型与正项式模型的复杂性比较

图6 EB-CFFE 测试误差与正项式预测能力的比较

3.2.3 与先进的不透明回归建模方法的比较

回归建模技术获得的不透明模型不具有可解释性，为此，比较它们的平均预测能力即平均预测误差(测试误差)。作为比较，选取了以下回归建模技术:常数、采用最小二乘拟合的线性模型(Linear Models with Least-Squares Fit，LM-LSF)、基于投影的二次方程式(Projection Based Quadratic，PBQ)、前馈神经网络(Feedforward Neural Network，FNN)、增强型FNN(Boosted-FNN，B-FNN)、多元自适应回归样条函数(Multivariate Adaptive Regression Splines，MARS)、最小二乘支持向量机(Least Squares-Support Vector Machines，LS-SVM)和克里格(Kriging)法。

模型生成器的编码和配置如下:构建常数、线性和完全二次型模型用MATLAB 代码实现，构建PBQ用Python 代码实现，采用数值/线性代数程序包进行最小二乘回归；对于增强型FNN，设置NumModels ＝20；MARS 模型构建器用MATLAB 代码实现；LS-SVM采用MATLAB 代码，所有设置为“全自动”；克里格模型构建器采用MATLAB 代码实现，设置Θmin＝0.0，Θmax＝10.0，pmin＝0.0，pmax＝1.99。

图7 所示为对于OTA 的6 个性能指标得到的平均预测误差(测试误差)。

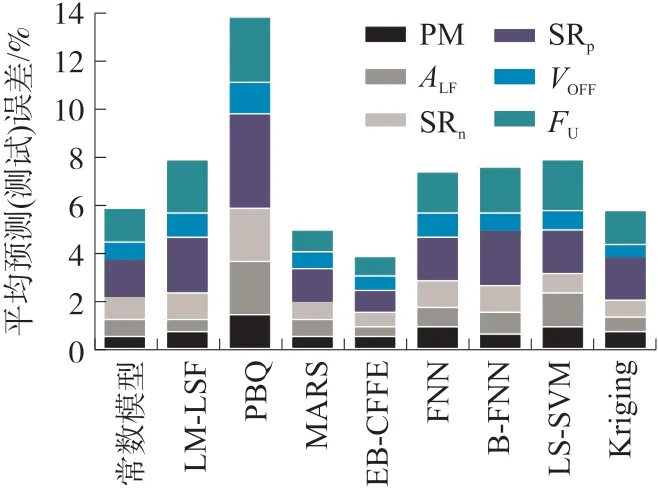
图7 EB-CFFE 与先进的回归建模技术的预测能力比较

可见，EB-CFFE 有最低的平均预测误差，MARS与之非常接近，克里格法次之。FNN、B-FNN 和LS-SVM 它们非常接近，与线性模型的性能基本相同，二次方程式方法最差；这是由于EB-CFFE 只选择真正重要的输入变量，它偏向于输入变量轴线，而不是仿射不变的。也就是说，EB-CFFE 表达式和搜索算子每次只处理一个或几个输入变量，而不是在加权和中使用所有变量。MARS 也类似，由于它逐步向前的特性使得它也偏向于轴线，并且对输入变量有选择性。在6 个性能目标中，EB-CFFE 有5 个预测误差最好或接近最好，MARS 有3 个预测误差最好或接近最好，克里格法有不错的预测性能，是因为当输入样本有相对均匀的间隔时，它趋向于执行较好，因为它采用DoE 采样；但克里格法、FNN 和B-FNN 比EB-CFFE和MARS 差，这很可能是因为它们对输入轴线没有有用的偏差(对于该应用)。B-FNN 的性能并不明显优于FNN，这意味着过拟合可能不是FNN 的问题；LS-SVM 的性能很差，可能是因为它对所选变量的处理过于一致；还可看到，只有EB-CFFE、MARS 和克里格法优于常数，而其他模型试图预测不可见的(测试)输入的输出效果很差，因为模型的泛化方向不好，导致更大的误差值，而常数没有过大的误差值。

4 结束语

本文提出了一种可以将非线性电路性能的可解释符号模型生成为电路的设计变量的函数的工具即EB-CFFE，无需预先要求模型模板；EB-CFFE 的主要思想是采用SPICE 仿真数据的流程，从仿真数据中提取无模板函数的多目标GP 搜索，以及用于可解释性的函数的规范形式约束；对模型的可视化测试表明模型是可解释的，对模型的性能实验表明比正项式更紧凑，比其他回归模型的平均预测误差也要低；所以，EB-CFFE 在健壮性建模、行为建模和权衡建模等应用中具有较好的前景。