基于灰色关联选取特征向量的BP神经网络岩相识别——以X油田A区部分井为例

梁旺东，王子龙

(1.中国建筑材料工业地质勘查中心宁夏总队，宁夏 银川 750021; 2.西安石油大学地球科学与工程学院，陕西 西安 710065)

目前研究区长62储层油藏剩余储量规模大、外围出油井点多，是宁夏地区二次加快发展主力军。但随着开发的不断深入，储层品质逐步变差、规模效益开发难度加大。主要存在储层致密、非均质性强、有利区优选难度大等问题，而岩相识别对于孔隙度渗透率模型的建立、油藏间砂体发育变化情况、主力含油小层的认识、储量的计算具有一定的实际指导意义。根据研究区的录井以及物性分析化验资料可知，长62层段主要发育黑色、灰黑色泥岩；灰色、深灰色、浅灰色细砂岩，常见砂、泥岩互层，沉积构造多为平行层理、砂纹交错层理、变形层理，其物性较差，非均质性较强，属于典型的特低渗岩性油藏。而主要的含油岩相为细砂岩，所以，前期测井工作中砂体的识别对于后期生产试油研究具有一定的实际意义[1]。

由于研究区井的数量较多，传统经验值统计法识别的准确性很大程度上依靠研究人员的地质经验和熟练度，并且具有识别效率低、工作量大、解释成果因人而异、泥岩和砂岩交界处识别困难界限不清晰、无法对砂岩进行精细细分等缺陷。因此，笔者提出一种基于灰色关联选取特征向量作为神经网络的敏感参数选取分析法，对研究区的目的层段选取影响因素最大的几种测井曲线进行岩相的精细识别，并且对网络本身参数进行优化，并提出ΔAC声波时差参数作为约束条件对模型进行优化。

1 基于灰色关联分析法测井系列敏感性因素的选取

1.1 鄂尔多斯盆地区域构造

X油田A区位于鄂尔多斯盆地，研究区长62油藏属三角洲前缘沉积，以水下分流河道沉积微相为主，位于天环坳陷构造单元，地层现今顶面构造整体呈现为两侧高、中部低。借鉴前人成果，A区发育近东西向逆断层，倾向多为南西方向。天环坳陷轴线以东，地层相对宽缓，天环坳陷轴线以西，毗邻西缘逆冲带，地层较为陡倾。区域概况如图1所示。

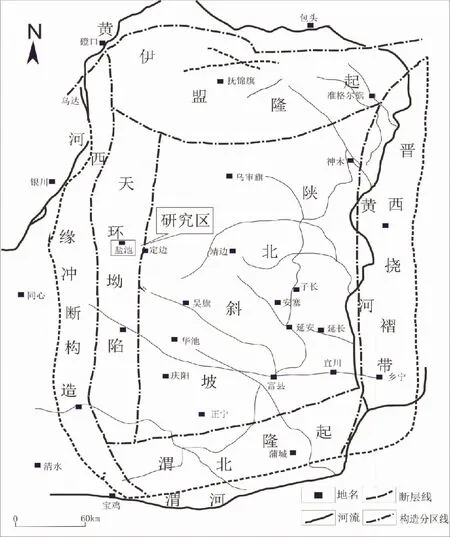
图1 鄂尔多斯盆地区域构造单元划分图及研究区位置图

1.2 灰色关联法方法原理

灰色关联分析法是一种多要素数学分析法[2-4]。在找寻样本序列与参考序列之间线性关系相似程度的过程中，找到反映样本序列与参考序列之间的关联度，对该序列进行指导。如果比较序列的变化态势和参考序列基本一致或相似，其同步程度较高，即可以认为两者关联程度较大；反之，两者关联程度较小。当信息系统不具有完全信息时，表明其具有“灰色”的性质。此时利用灰色系统评估方法进行绩效评价非常实用，按照这一分析思想就不会出现异常。此外，灰色关联分析法无论获取到多少数据都可以进行分析，而且能具体问题具体分析后进行量化分析。

灰色关联分析模型中包括均权关联度模型和加权关联度模型，两者的不同之处为加权关联模型给各个参数赋予了不同的权值，而均权关联度模型相当于认为各参数的贡献是等价的，权值始终为1，2种模型的表达式分别为：

均权关联度模型：

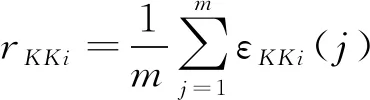
(1)

加权关联度模型：

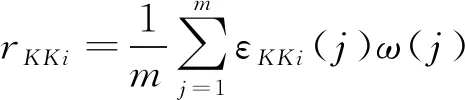
(2)

式中：rKKi为参考要素序列与比较要素序列的关联度；εKKi(j)为参考要素序列与比较要素序列第j个参数的关联系数；ω(j)为关联系数的权重。

1.3 灰色关联法的分析过程

灰色关联法的分析过程主要包括以下5个步骤，如图2所示。

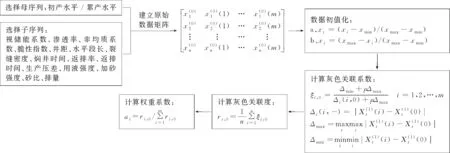
图2 灰色关联分析过程步骤

1.4 灰色关联法功能与应用

灰色关联度法提出对各子系统进行灰色关联度分析的概念，试图通过一定的方法去寻求系统中各子系统之间的数值关系[5]，其是以各种影响因素的样本数据作为依据，用灰色关联度描述各种影响因素之间关系的强弱、大小和次序，该方法的优点在于思路明晰，可以在很大程度上减少因信息不对称带来的损失，且对数据要求较低、工作量较少。

通过对自然伽马、自然电位、中子、电阻率、孔隙度等测井参数进行关联度分析，结果如图3所示。

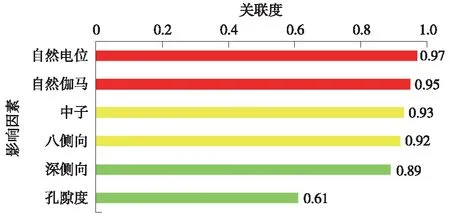
图3 A区岩性影响因素灰色关联分析结果

从图3中可以看出，各影响因素的关联度分布在0.61～0.97范围内，关联性强，A区岩性划分主控因素排序为：自然电位>自然伽马>中子>八侧向>深侧向>孔隙度，其中自然电位和自然伽马的关联度最高。

选取自然电位和自然伽马作为神经网络输入层的特征向量。

白城市棚膜种植仍以传统型、大路货为主，缺少特色品种和稀有品种，没有形成品牌优势，产品知名度不高，市场竞争力不强。

2 神经网络原理

BP神经网络是一种按照误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络基础模型之一[6-9]。BP网络可学习、存贮大量输入-输出模式的映射关系，且无需事先通过这种映射关系的数学方程来描述[10-11]。BP神经网络的结构如图4所示。

图4 神经网络结构示意图

每种特征向量会因为其数量级不同而导致网络训练的收敛时间变长，训练时间变慢[12-13]；数据范围变化大的特征向量会导致其对分类结果的影响作用变大，数据范围小的特征向量会对其分类结果的影响变小[14]；因神经网络输出层特征向量对于激活函数的值域范围是有限制的，所以需对网络训练的目标输出层数据映射到激活函数的值域范围内。如果神经网络的输出层采用S形激活函数，因S形函数的值域范围限制在(0，1)，即神经网络的输出层数据只能限制在(0，1)，所以对于训练数据的输出就要归一化到[0，1]区间；S形激活函数在(0，1)区间之外的区域很平缓，区分度太小，所以将其归一化到(0，1)区间内可增加区分度。

以上种种因素要选取网络训练特征参数x1，x2，…，xn，然后对选取的特征向量进行归一化操作。常见归一化的方法有以下2种计算方式[15]：

Y=(x-min)/(max-min)

(3)

Y=2*(x-min)/(max-min)-1

(4)

式中：x为每一个训练参数，max为所有训练参数中的最大值，min为所有训练特征参数中的最小值。

设BP神经网络的输入向量X=(x1，x2，…，xn)，隐含层输出向量是H=(h1，h2，…，hn)，输出层输出向量和期望输出向量分别是Y=(y1，y2，…，yn)；对样本中选取一定的训练集、测试集，然后通过训练集建立相应的神经网络模型。利用剩余的测试集进行模型性能的检验得出模型的性能并且对其进行优化，得到一个较好的模型。目前在碳酸盐岩以及火成岩等岩性的识别中得到很好的应用。

3 研究区BP神经网络模型的建立与优化对比

3.1 研究区岩性划分的经验统计值法

研究区已有的数据统计表明，该地区自然伽马具体分布范围如表1所示。

表1 研究区自然伽马分布情况

由于该地区的自然电位曲线对砂体识别曲线异常不是特别敏感，对此，选取自然伽马值作为划分依据。由表1中可以看出，研究区的自然伽马值在0～20范围内没有分布；20～40范围内分布5个数值点；40～60范围内分布247个数值点；60～80范围内分布2111个数值点；80～100范围内分布919个数值点；100及以上分布49个数值点。其中自然伽马值主要分布在40～100之间。按照经验值法识别的砂体结果如图5所示。

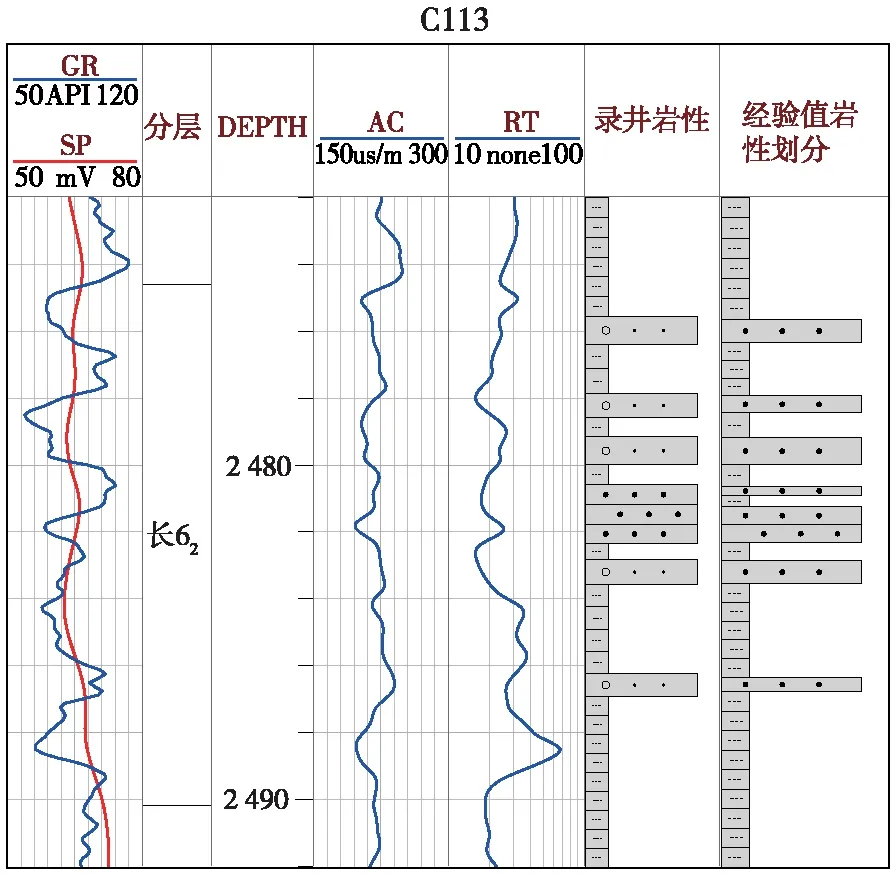
图5 C113井研究区经验值法岩相预测与实际岩性划分结果对比

3.2 研究区特征参数的选取

在神经网络的参数选取中并不是特征向量越多越好，参数多会导致神经网络训练时间长、准确率并不会得到提高，所以在已有测井资料数据自然伽马、自然电位、中子、电阻率、孔隙度5个测井系列中选取关联度最高的2个作为神经网络的输入层，简化了神经网络结构，提高神经网络训练速率。

通过前人的经验以及灰色关联法分析得到，常规测井中自然电位和自然伽马测井系列可以很好地解释识别岩相，常见典型岩石的测井特征如表2所示[16-17]。

表2 常见砂泥岩的测井响应特征

通过灰色关联分析法选取关联度最高的岩性测井系列中的自然伽马测井曲线数据以及自然电位测井曲线数据作为神经网络模型特征向量输入层，然后以声波时差参数作为输出结果的约束条件，对BP神经网络的建模预测结果进行优化。

3.3 研究区砂体预测神经网络模型的建立

(1)选取特征向量自然电位和自然伽马，记自然伽马为x1n，自然电位为x2n，则输入层矩阵为：

X=(x1，x2)

(5)

(2)对输入层函数利用mapminmax函数进行归一化处理。

(3)对神经网络的网络结构参数进行设置，隐含层节点数设置为8，训练迭代次数设置为1 000，学习速率设置为0.1，训练目标的最小误差设置为0.1。

(4)对网络参数进行设置。本次建模一共有313个数据样本，其中选取80%的输入层样本作为训练集，15%的训练样本作为验证集，5%作为测试集。隐含神经元设置为10个，隐含层数设置为2个，然后对网络模型进行训练。其预测结果如图6、图7所示。

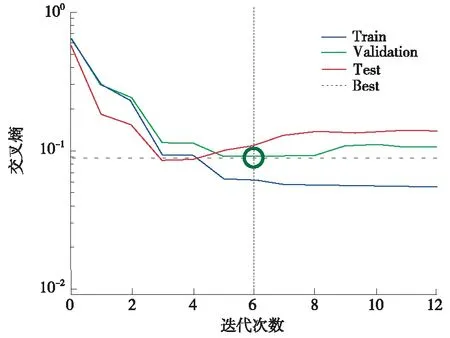
图6 神经网络性能验证图

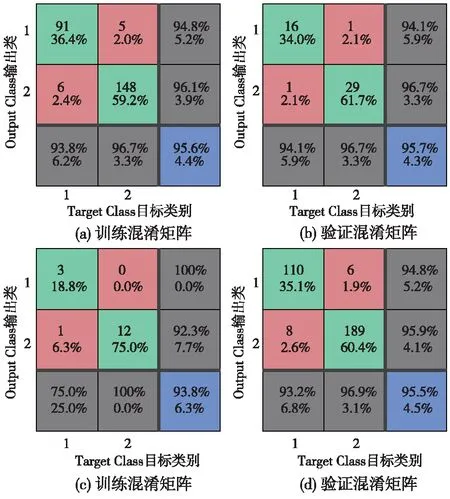
图7 神经网络预测准确率分布图

从图6中可以得出，该模型在迭代次数为6时，训练误差为0.088 26，达到训练要求，停止训练。训练集的预测准确率可以达到95.6%，验证集的预测准确率可以达到95.7%，测试集的预测准确率可以达到93.8%，所有结果的综合预测准确率可以达到95.5%。综上所述，对于砂体的识别准确率有着一个比较理想的结果，如图8所示。

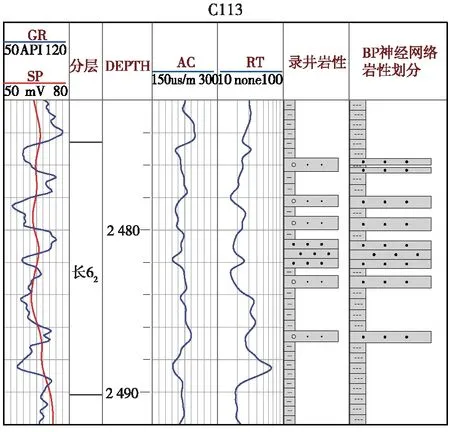
图8 C113井神经网络岩相划分与实际岩相划分结果对比图

从图8中可以看到，细砂岩、泥岩、砂岩的预测结果和曲线划分的结果基本吻合，可以满足在实际岩性划分研究中对砂岩的识别的准确进度要求。

3.4 模型的优化

以上建立的模型已经达到一个比较理想的效果，但是2 469.9～2 470.375 m的岩性预测结果不符合实际结果。所以在此对该模型通过建立声波时差参数对模型预测准确性进行优化。

通过对研究区的声波时差数据统计发现，该地区的泥岩声波时差225.69 μs/m要略大于砂岩的声波时差214.42 μs/m，并且在砂泥岩的交接处附近声波时差的变化较大，通过构建ΔAC对模型进行优化：

ΔAC=|AC1-AC5|

(6)

其中：AC1为交界处的第1个声波时差值;AC5为第5个交界处的声波时差值。研究区的ΔAC值统计结果如表3所示。

表3 ΔAC统计数据表

由表3中可以看出，研究区的ΔAC值在10.61～20.87范围内。由测井数据可得，C113井的划分错误的深度范围2 470～2 470.25 m，这部分点的测井数据的平均值为213.78，ΔAC值为3.95，变化范围较小，所以可以对该段的岩性进行校正，从而提高模型的准确率。预测结果如图9所示。

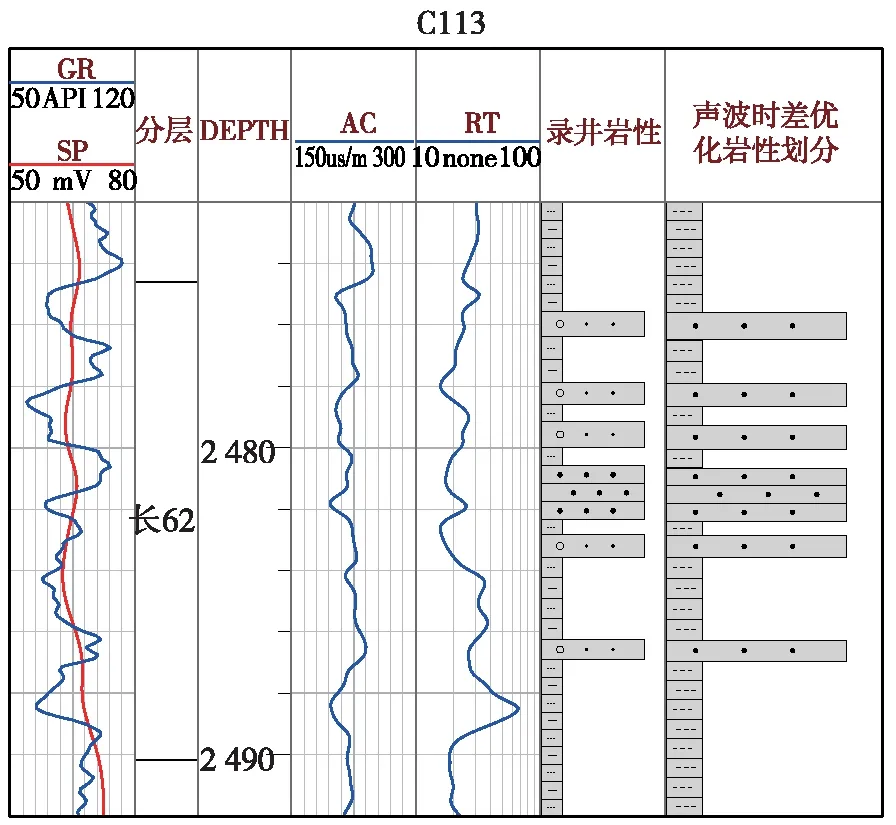
图9 神经网络岩性预测优化后与实际岩性划分结果对比图

从图9中可以看出，通过建立声波时差参数ΔAC对模型进行优化，可以使BP神经网络预测泥岩夹层误差得到优化且准确率更高。预测结果基本和划分结果一致。

4 结论

(1)利用灰色关联法选取研究区长62的自然电位、自然伽马、中子、八侧向作为神经网络的输入层建立神经网络模型，结果表明，岩相预测准确率达到95.5%；利用ΔAC参数对模型进行优化，得到岩相识别的准确度达97.6%。

(2)该方法能很好地利用敏感参数对研究区进行岩相识别，并且预测误差率控制在10%以内，由于不同区块的地质差异，可以对该模型通过参数重新配置，具有适用于该油田的其他区块进行岩相识别的潜力。