一种切向入口倒锥式旋流器最大磨蚀率方程模型的构建
裴金源,张 勇*,胡 卫,宋晶鑫
(1.东北石油大学机械科学与工程学院,黑龙江 大庆 163318; 2.武汉迈力特通信有限公司,湖北 武汉 430000;3.大庆油田有限责任公司第五采油厂,黑龙江 大庆 163318)
旋流器根据互不相容介质存在的密度差通过离心力作用将介质分离。因其结构简单、分离效率高、工艺流程简便,广泛应用于石油开采、石油石化污水处理等相关领域[1-4]。倒锥式旋流器利用倒锥结构在分离锥段部分形成过流空间的二次变化,并对中心轻质相的运移起到稳定作用,可适用于井下油水分离及同井回注工艺中[5]。但是,井下环境由于井液含砂容易引起倒锥式旋流器入口、内壁及出口部分的磨蚀,影响旋流分离器的效果,进而降低井下分离系统的稳定分离使用寿命。
杨兆春[6]基于环形管流场对旋流器壁面磨蚀问题进行分析,将旋流器磨蚀主要分为固相颗粒冲击和滑动摩擦2种磨蚀状态。卢梦媚等[7]针对旋流器磨蚀问题,在其内部设计一种内嵌小锥结构,可以延长旋流器的使用寿命。Zhang等[8]从冲蚀角度方面形成了颗粒对旋流器壁面的冲蚀破坏机理。贺红霞等[9]运用数学推导获得了一种适用于旋流管磨蚀的数学模型。Jung等[10]对旋流器螺旋流道部分进行优化改进,进而提高了旋流器对固相颗粒的捕集效率并降低了旋流器壁面的磨蚀程度。阎安等[11]使用耐磨蚀材料对旋流器进行制造,并提高旋流器壁面的加工质量,从而延长了旋流器的使用寿命。Daza等[12]探究了进液粒度和入口压力对旋流器内部污垢凝结的影响,当固相颗粒表面粗糙时,结垢现象明显且旋流器壁面磨蚀严重。Li等[13]设计一款新型耐磨蚀旋流器可有效去除废水中的固相颗粒。Chang等[14]通过对水力旋流器结构进行改进,提升了旋流器的抗磨蚀效果。龚伟安[15]将旋流器内部表面喷涂耐磨涂层,进而提高使用寿命。刘宏钢等[16]对旋流器进行数值模拟与实验,获得了某型旋流器各段的磨蚀曲线。国内外学者致力于获得流体含砂对旋流分离的影响,但是并未形成规律认识,也无法对磨蚀率形成预测。
切向入口倒锥式旋流器具有结构紧凑、分离效率高、占地面积小等特点,可有效用于气液、固液、液液、气液固等多相介质的分离,其常被应用于各大油田,因此笔者以一种用于井下油水分离的切向入口倒锥式旋流器为例,基于离散相模型(Disperse Phase Model,简称DPM)进行数值模拟,获得不同参数对壁面磨蚀的规律,获取对切向入口倒锥式旋流器最大磨蚀率影响的关键因素,进而采用响应面法对固相颗粒进液流速、固相颗粒浓度、固相颗粒粒径3个主要磨蚀影响因素进行交互影响分析,综合形成旋流器壁面最大磨蚀率的多元回归拟合方程模型。
1 理论模型及受力分析
1.1 基本控制方程
旋流器内部流场具有强烈旋转的特性,内部流域不可压缩,符合雷诺应力模型 (RSM) 特性,RSM 摒弃了流动各向同性的假设理论,理论上其具有更高的精度[17]。其基本控制方程为[18-19]:
质量守恒方程为:
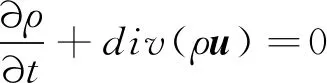
(1)
式中:ρ为密度(kg/m3);u为矢量速度(m/s);t为时间,s。
动量守恒方程为:
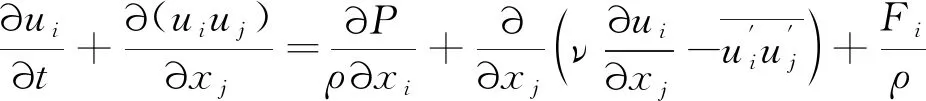
(2)
式中:ui、uj分别为速度分量(m/s);ν为动力黏度(Pa·s);P为压力(Pa);Fi为广义源项。
雷诺应力控制方程为:
Pij+φij+εij+Fij
(3)
式中:Pij为剪切应力源项;φij为压力应变源项;εij为黏性耗散源项;Fij为系统旋转源项。
1.2 磨蚀模型
利用DPM模型中的Erosion模型作为磨蚀仿真的理论模型[20-22],公式如下:
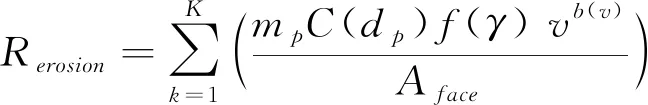
(4)
式中:Rerosion为磨蚀率,kg/(m2·s);mp为粒子质量流量,kg/s;C(dp)为粒子粒径函数;f(γ) 为入侵角函数;v为粒子速度,m/s;b(v)为粒子速度函数;Aface为受冲击壁面单元面积,m2。
2 计算模型和边界条件
2.1 物理模型选定
井下切向入口倒锥式旋流器结构如图1所示,其具体结构尺寸如表1所示。

表1 倒锥式旋流器尺寸参数
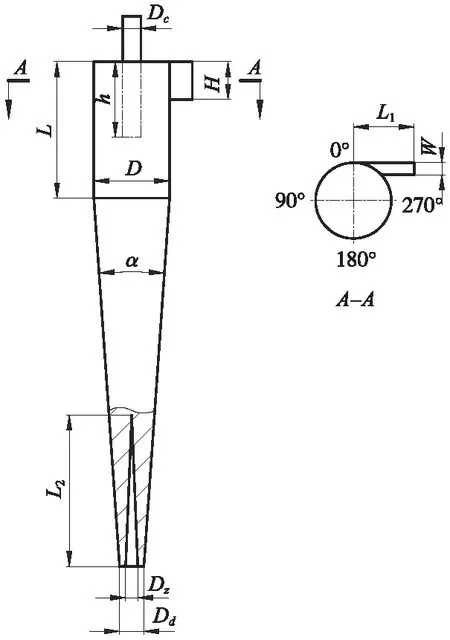
图1 倒锥式旋流器尺寸
2.2 边界条件设定
倒锥式旋流器入口及柱段部分是形成旋流场的重要区域,同时也是流动速度最高的部分,其磨蚀情况最为严重[23],因此将该区域的最大磨蚀率作为磨蚀率规律形成的参照数据。
处理介质以大庆油田某同井注采井的井液数据为对象,以仿真软件Fluent对此旋流器展开数值模拟。在软件中设定水相为连续相,离散相设为砂相固相颗粒,将固相颗粒粒形近似为球形。离散相以与连续相相同的速度从入口处注入。采用压力-速度耦合为SIMPLE,压力离散格式采用PRESTO,动量离散格式采用QUICK。运算时先对连续相进行求解,后续开启DPM模型加入粒子,保证了运算的精度和稳定性。
3 结果分析
液体连续相中固相颗粒对壁面磨蚀形式的主要因素包括固相颗粒进液流速、固相颗粒浓度、固相颗粒粒径、固相颗粒形状及固相颗粒的密度等,其中,一般将井下砂相的形状等效为球形,因此首先对其他4个参数含砂井液特性对倒锥式旋流器壁面磨蚀的程度进行仿真和分析,进而采用响应面方法获得影响因素间的相互作用关系,最终形成倒锥式旋流器壁面磨蚀的最大磨蚀率方程式模型。
3.1 固相颗粒进液流速对倒锥式旋流器壁面磨蚀的程度分析
大庆油田某实验现场工况选用6~14 m/s的流速范围进行模拟,获得的入口及圆柱段壁面磨蚀云图如图2所示。由图2中可以看出,随着入口进液流速的增大,固相颗粒在离心力的作用下被甩到壁面的几率增加,与壁面相互作用的能量也获得提升,磨蚀的影响范围逐步增大,磨蚀程度也相应增加。各流速条件下入口及圆柱段范围内壁面最大磨蚀率的关系曲线如图3所示,由图3中可以看出,壁面最大磨蚀率随着进液流速呈指数趋势增大,最大磨蚀率由10-6kg/(m2·s)数量级增至10-4kg/(m2·s)数量级。因此,判定固相颗粒进液流速为最大磨蚀率影响的主要因素之一。

图2 不同固相颗粒进液流速对入口及圆柱段壁面磨蚀云图
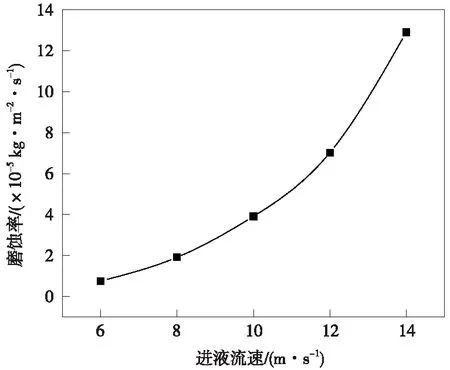
图3 固相颗粒进液流速对入口及圆柱段壁面最大磨蚀率曲线
3.2 固相颗粒浓度对倒锥式旋流器壁面磨蚀的程度分析
根据大庆油田在采油井口的采出液含砂量选定固相颗粒质量分数为1%~9%,获得的入口及圆柱段壁面磨蚀云图如图4所示。从图4中可以看出,固相颗粒质量分数增加相应提高了固相颗粒与壁面的碰撞机会,固相颗粒质量分数对入口及圆柱段壁面磨蚀的程度和范围影响很大。固相颗粒对入口及圆柱段壁面磨蚀的影响曲线如图5所示。由图5中可以看出,壁面最大磨蚀率随着质量分数呈正相关趋势增大,最大磨蚀率由10-6kg/(m2·s)数量级增至10-5kg/(m2·s)数量级,因此判定固相颗粒质量分数为最大磨蚀率影响的另一个主要影响因素。

图4 不同固相颗粒质量分数对入口及圆柱段壁面磨蚀云图
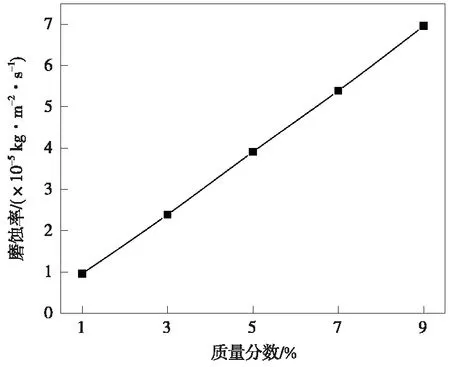
图5 固相颗粒质量分数对入口及圆柱段壁面最大磨蚀率曲线
3.3 固相颗粒粒径对倒锥式旋流器壁面磨蚀的程度分析
利用马尔文粒度仪测得大庆油田采出液中固相粒径集中在10~50 mm范围内,其粒径中值为0.03 mm。粒径对倒锥式旋流器入口及圆柱段壁面磨蚀的仿真结果如图6所示。由图6中可以看出,固相颗粒粒径增加同样带来壁面磨蚀的范围和程度的增大。固相颗粒对柱段壁面磨蚀的最大磨蚀率曲线如图7所示。由图7中可以看出,随着粒径的增大,入口及圆柱段壁面最大磨蚀率由2.36×10-5kg/(m2·s)增至1.04×10-4kg/(m2·s),影响显著,因此判定固相颗粒粒径可作为最大磨蚀率影响的另一个主要影响因素。

图6 不同固相颗粒粒径对入口及圆柱段壁面磨蚀云图
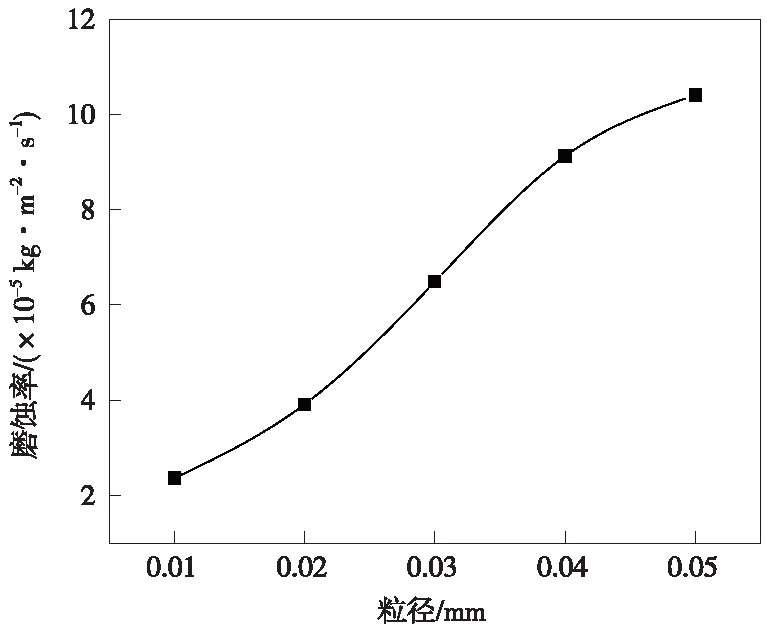
图7 固相颗粒粒径对入口及圆柱段壁面最大磨蚀率曲线
3.4 固相颗粒密度对倒锥式旋流器壁面磨蚀的程度分析
我国主力油田的砂相颗粒密度范围为2 000~2 200 kg/m3。固相颗粒密度对倒锥式旋流器入口及圆柱段壁面的磨蚀的影响如图8所示。由图8中可以看出,在此密度变化范围的磨蚀范围和磨蚀程度变化不大。壁面最大磨蚀率曲线如图9所示。由图9中可以看出,壁面最大磨蚀率在3.9~4.04 kg/(m2·s)范围内,相对于固相颗粒进液流速、固相颗粒质量分数、固相颗粒粒径这3个因素,固相颗粒密度的改变对壁面最大磨蚀率的影响较为稳定,因此,可在考查参数对最大磨蚀率的影响规律时设定其为一定值。

图8 不同固相颗粒密度对入口及圆柱段壁面磨蚀云图
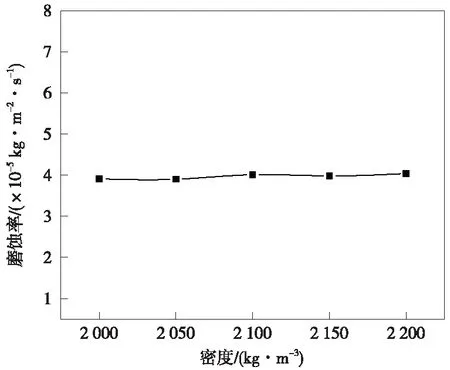
图9 固相颗粒密度对入口及圆柱段壁面最大磨蚀率曲线
3.5 多因素交互影响关系
基于响应面优化方法对磨蚀效果影响显著的固相颗粒进液流速、固相颗粒质量分数、固相颗粒粒径3个显著因素进行响应分析,进而拟合出最大磨蚀率在以上3个因素交互影响下的通用预测方程。采用Box-Behnken Design方法进行设计,设计因素及水平如表2所示。

表2 响应面试验因素与水平
基于响应面数据分析法将上述数据进行整理,产生17组组合数据,将每组数据进行仿真并得出最大磨蚀率,如表3所示。
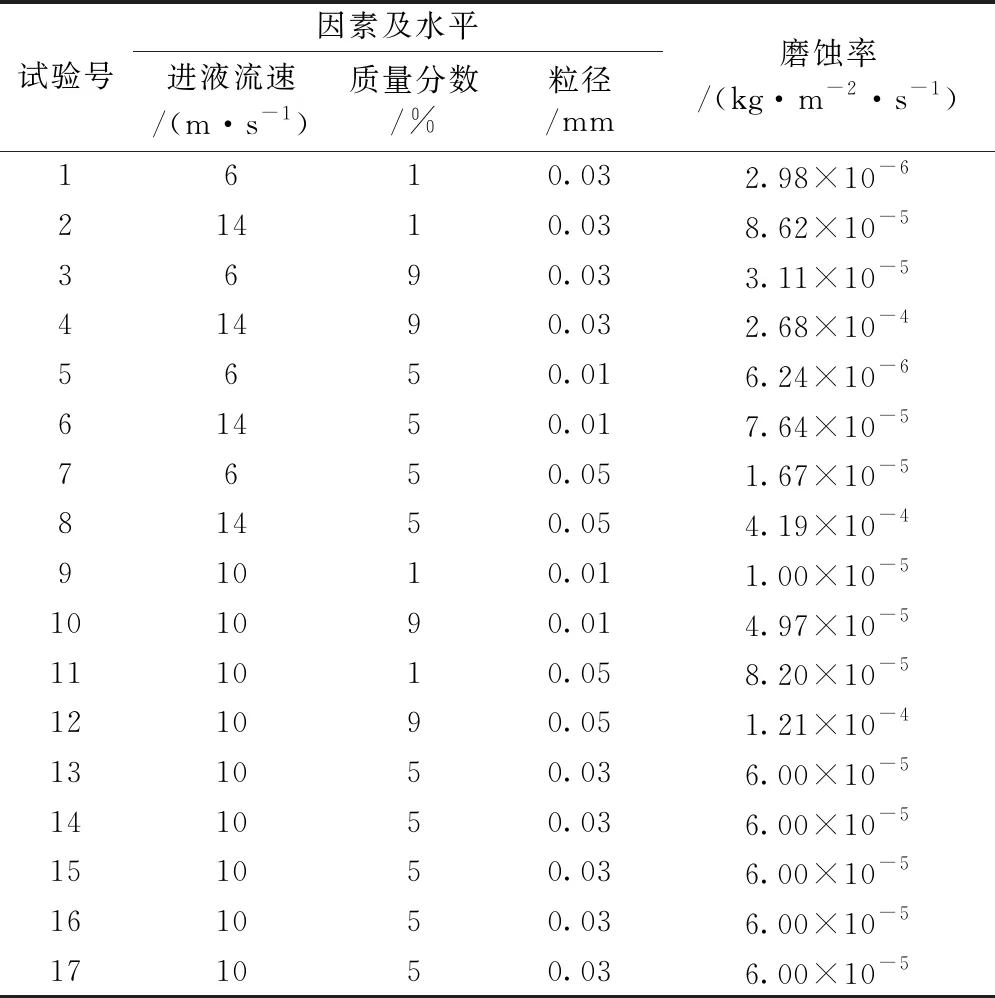
表3 响应面试验方案及指标值
对固相颗粒进液流速A、固相颗粒质量分数B、固相颗粒粒径C三因素影响壁面最大磨蚀率的程度进行拟合,可获得壁面最大磨蚀率Y的多元回归拟合方程,使磨蚀影响分析的结果具有普适性:
Y=4.427×10-4-8.148×10-5A-6.534×10-6B-1.013×10-2C+2.401×10-6AB+1.038×10-3AC-2.188×10-6BC+3.155×10-6A2-8.394×10-7B2+4.771×10-2C2
(5)
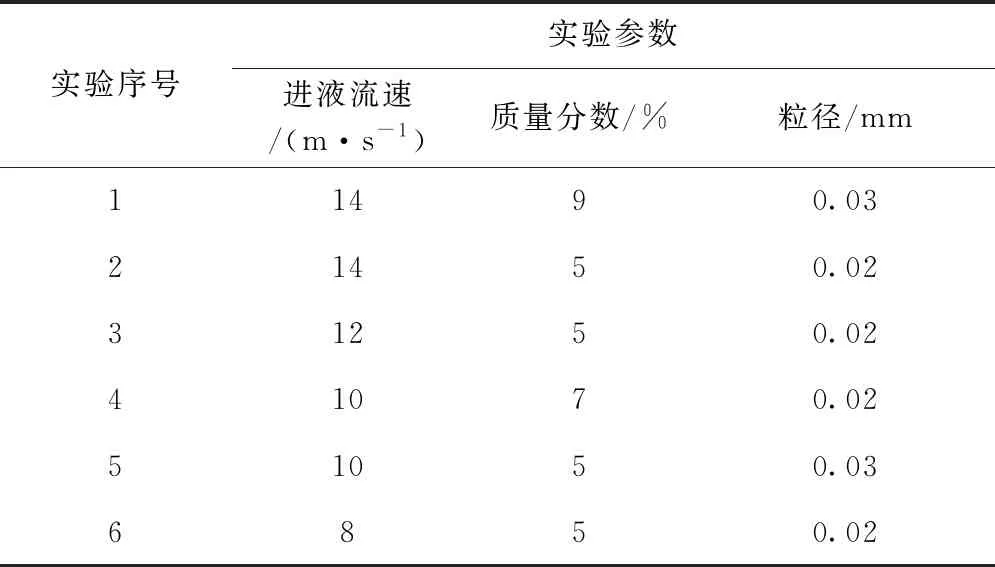
该公式是根据进液流速为6~14 m/s、质量分数为1%~9%、固相颗粒粒径为0.01~0.05 mm的井下工况进行拟合获得,可适用于大庆油田井下所配置旋流器的寿命计算。利用方差分析法将操作参数与壁面最大磨蚀率所构建的多元回归拟合方程进行检验,方差分析结果如表4所示。由表4中可以看出,固相颗粒进液流速、固相颗粒浓度、固相颗粒粒径这3个操作参数与壁面最大磨蚀率构建的多元回归拟合方程模型P值为:0.0001 表4 方差分析结果 对得到的多元回归拟合方程模型进行误差统计分析,从而验证方程的准确性。R-Squared 表示多元回归拟合方程模型的相关系数,通过响应面分析法得到R-Squared数值为0.940 3,其数值越接近1,表明多元回归拟合方程模型的相关性越好;得到的Adeq Precision 数值为13.646,Adeq Precision的数值大于4,则表明该模型具有良好的合理性。综上所述,通过误差统计分析,表明该多元回归拟合方程模型应用良好。 为了验证当固相颗粒进液流速、固相颗粒质量分数、固相颗粒粒径影响下的壁面最大磨蚀率多元回归拟合方程模型的准确性,在各操作参数的上下极限内随机选取,累计开展6组实验进行验证,室内实验流程如图10所示,室内实验现场如图11所示。每组实验运行10机时,实验的操作参数取值如表6所示。 图10 室内实验流程图 图11 室内实验现场 表6 实验操作参数 将以上6组实验参数代入式(5),得到模型预测值与实测值的对比情况,如图12所示。为了进一步对模型精度进行检验,采用式(6) 和式(7)分别进行相对误差计算与平均相对误差计算,模型预测值与实验测值最大相对误差为4.91%,平均相对误差为3.52%,可以看出模型预测值与实际值间的平均相对误差很小,验证了模型预测结果的准确性,因此,该模型可用于切向入口倒锥式旋流器磨蚀程度和使用寿命的预测。 图12 模型预测值与实验测值对比 (6) 式中:p为模型预测值,kg/(m-2·s);t为试验测值,kg/(m2·s)。 (7) 式中:i为实验序号;n为实验组数。 (1)井下切向入口倒锥式旋流器在含砂井液作用下,入口及圆柱段区域受固相颗粒进液流速、固相颗粒质量分数和固相颗粒粒径的影响显著,在工作参数的区间范围内入口及圆柱段区域最大磨蚀率分别随着这3个参数值的增大显著增加。 (2)基于响应面法可综合考虑固相颗粒进液流速、固相颗粒质量分数和固相颗粒粒径的交互影响,形成涵盖此3个参数的多元回归拟合方程模型,构建的操作参数与磨蚀率预测模型的相关系数R-Squared为0.940 3,表明该模型具有一定的精确性。 (3)实验验证表明,得到的壁面最大磨蚀率多元回归拟合方程模型对井下切向入口倒锥式旋流器最大磨蚀率的预测效果良好,模型预测值与实验测值最大相对误差为4.91%,平均相对误差为3.52%,验证了模型预测结果的准确性,该模型可用于井下切向入口倒锥式旋流器在井下含砂环境使用时最大磨蚀程度和使用寿命的预测。
3.6 最大磨蚀率元回归拟合方程模型的实验验证



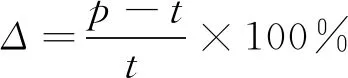
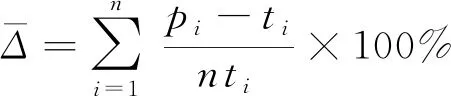
4 结论

