直接蒸汽光热发电系统中相变换热器的传热特性研究

王文昭，郑乐飞，邓雅军，宇波，孙东亮

(北京石油化工学院机械工程学院， 北京 102617)

我国二氧化碳排放力争于2030年前达到峰值，努力争取2060年前实现碳中和。大力发展太阳能、风能等可再生能源对调整我国能源结构、减少碳排放具有重要意义。然而，可再生能源最大的问题在于其不连续和不稳定性，可再生能源发电在并网时会对电网造成较大的冲击。相对于光伏与风力发电，储热型太阳能热发电技术一般采用汽轮发电机组，光照充足时将一部分太阳能转化成热能储存，在傍晚之后或者电网需要调频调峰时用于发电以满足电网的要求[1-2]。太阳能光热发电系统的传热流体(heat transfer fluid, HTF)主要有水、导热油和熔融盐等。水作为传热介质具有无污染、无腐蚀、价格便宜等优点，且蒸汽发生技术成熟，吸热后产生的高温高压蒸汽可直接驱动汽轮机，从而减少热量传递过程中的能量损失，因而具有很好的应用前景[3]。

光热发电系统中配备蓄热系统至关重要。目前太阳能光热发电的蓄热技术主要有3种：显热蓄热、潜热蓄热和热化学蓄热[4]。显热蓄热的优点在于原理简单、技术成熟、可用材料广泛且廉价，但显热蓄热的储热密度较低，蓄热装置体积一般较大[5]。热化学蓄热技术难度较高、约束条件苛刻，并且由于化学反应的不可控以及蓄热器较复杂，目前还不够成熟[6]。潜热蓄热是利用物质在相变过程中吸收潜热的原理蓄热。相较于显热蓄热材料，相变蓄热材料(phase change material, PCM)具有相变潜热高、相变时温度变化小以及相变蓄热的蓄热密度更大等优点[7-9]。因此，太阳能热发电系统受到越来越多的重视[10-12]。

很少有人关注在考虑自然对流存在时直接蒸汽相变蓄热器的流动与传热情况，并且大部分研究在模拟管内蒸汽冷凝时均采用一维简化模型。因此，笔者建立了管内二维蒸发冷凝模型并与管外PCM考虑自然对流的融化凝固模型相耦合构成管壳式直接蒸汽蓄热模型，并研究自然对流对直接蒸汽相变蓄热器数值模拟结果的影响。

1 物理模型

蓄热单元结构如图1所示。管内换热流体是工作压力为10.7 MPa的饱和蒸汽，其入口质量流量为50 kg/h。NaNO3作为相变材料填充在管外环形空间，蓄热单元内径为26.1 mm，外径为131 mm，长为5 000 mm。饱和蒸汽和熔融盐的热物性参数如表1所示。

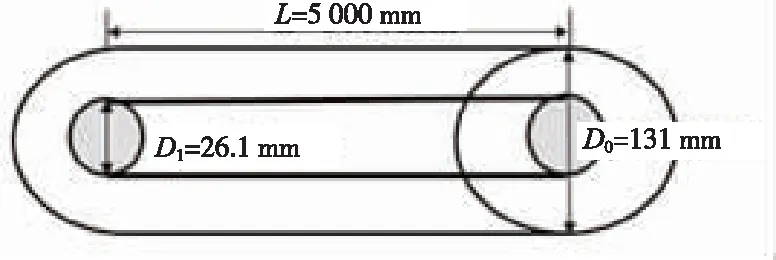
图1 蓄热单元结构示意图

表1 饱和蒸汽及NaNO3的热物性参数

为了减小计算量，缩短计算耗时，有效地提高数值模拟计算效率，数理模型采用以下简化与假设：

(1)忽略相变材料液体与固体之间的密度差，因此蓄放热过程中相变材料体积固定不变；

(2)相变蓄热系统是轴对称模型，使用二维轴对称模型模拟相变材料与换热流体之间的热传递；

(3)为模拟液态熔盐时的自然流动，采用Boussinesq近似处理液态熔盐的密度场；

(4)相变材料是均匀各向同性且具有固定的相变温度；

(5)管壁的厚度和热阻都忽略不计；

(6)换热流体的入口速度和入口温度恒定。

2 数学模型

2.1 管内蒸汽冷凝过程

对于换热流体涉及到气液相变，常用VOF模型、mixture模型以及欧拉模型来模拟多相流动，但是Fluent软件内部只允许VOF模型与Solidification and melting模型一起使用。因此，管内饱和蒸汽气液相变的数值计算采用VOF模型。基于Lee模型来确定能量方程源项[18]，进而模拟管内饱和蒸汽的冷凝过程。对应管内饱和蒸汽的控制方程如下:

连续性方程：

(1)

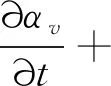
(2)

动量方程：

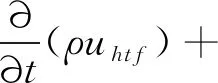
(3)

能量方程：

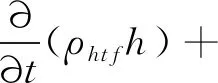
(4)

2.2 管外相变材料融化过程

对于相变材料，采用Fluent内部的Solidification and melting模型来模拟PCM的整个融化过程及固液相变过程中的界面移动。该模型采用的是Voller[19]提出的焓-孔隙率方法，是在模拟相变蓄热过程中将PCM的温度与焓一起看作求解变量，无需建立单独的控制方程，可以对整体的固相区、液相区及糊状区建立统一的守恒方程。模型的核心是将含有固相和液相的区域定义为糊状区，这一区域被当作多孔介质考虑，孔隙率与液相分数成正比，随着材料固化，孔隙率从1降至0。液相分数β定义为：

(5)

由于焓-孔隙率方法将糊状区视为多孔介质，而在完全凝固的区域中，孔隙率等于零，这些区域中的速度为0，所以添加动量方程源项S，其形式为：

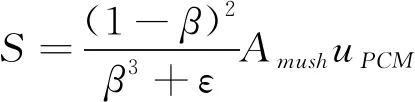
(6)

其中：ε是一个值为0.001的常数，避免分母为零；u为PCM的速度；Amush为糊状区常数，一般为105～107，具体的取值需根据实际的物理模型以及PCM材料的物性来确定[20]。

相变材料的焓是显焓与相变潜热之和，其中总焓H表达式为：

(7)

其中：ΔH=βL；href为相变材料的焓值；T为相变材料的温度；Tm为相变材料的熔点；cp为相变材料的比热容；L为相变材料的潜热。

Boussinesq假设对密度场的近似处理是将除动量方程以外的其他控制方程中的密度作为常数。此项中的密度随温度变化，可根据下式计算得到：

ρ=ρ0(1-β·ΔT)

(8)

其中:ΔT为实际温度与参考温度T0之间的温差；ρ0为参考温度下的密度。

因此，PCM部分的控制方程为：

连续性方程：

∇·uPCM=0

(9)

动量方程：

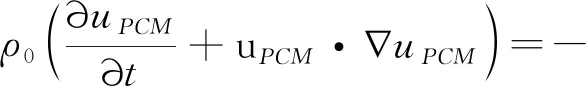
(10)

能量方程：

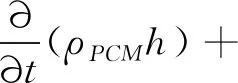
(11)

其中：θ=T-Tm，T为相变材料温度，Tm和λ分别为相变材料的相变温度与导热率。

2.3 边界条件与初始条件

边界条件为：蓄热器表面为绝热边界；内管与外管之间采用耦合边界；入口为速度入口，出口为Outflow边界条件。

初始条件为：相变材料温度为578.15 K；传热流体温度为589.15 K。

2.4 数值方法

为提高管内饱和蒸汽冷凝过程的模拟精度，边界层网格的划分对计算精度至关重要，因此，对换热壁面进行边界层加密。经过网格无关解验证，绘制了如图2所示的800×55网格示意图，此数目的网格同时具有较高的计算精度及较好的计算效率。

图2 蓄热器网格划分示意图

直接蒸汽相变蓄热器的蓄热过程属于非稳态、较高流速的多相流问题。因此，选用分离式求解器中更加适用于瞬态问题的FSM(Fractional step method)算法对其进行数值模拟研究。并且能量方程采用二阶迎风差分格式离散，动量方程采用QUICK格式离散，压力项采用PRESTO!离散格式，连续性方程与动量方程残差为10-3，能量方程残差为10-6。

由于直接蒸汽相变蓄热器的初始阶段换热剧烈。因此，数值模拟前期取较小的时间步长，以获得前期较为稳定的速度场与温度场，待残差曲线稳定后逐渐加大时间步长，控制全局库朗数不超过5。

2.5 模型验证

因为直接蒸汽相变蓄热的实验数据难以获得，所以目前大多研究为数值模拟，为验证模型合理性及方法可靠性，对Ju[11]的数值模拟结果进行了对比验证。以10.7 MPa下的饱和蒸汽为传热介质，NaNO3为蓄热材料，采用套管结构蓄热单元对NaNO3的熔化相变过程以及蒸汽冷凝过程进行数值模拟研究，以前文设定模型为基础，取与文献[11]相同的蓄热介质、传热介质、初始条件和边界条件进行数值模拟。PCM液相质量分数以及出口蒸汽体积分数随时间变化曲线与文献的对比结果如图3、图4所示。由图3、图4中可以看出，所用的模型与文献中的数据具有较好一致性，后续研究均采用此模型。

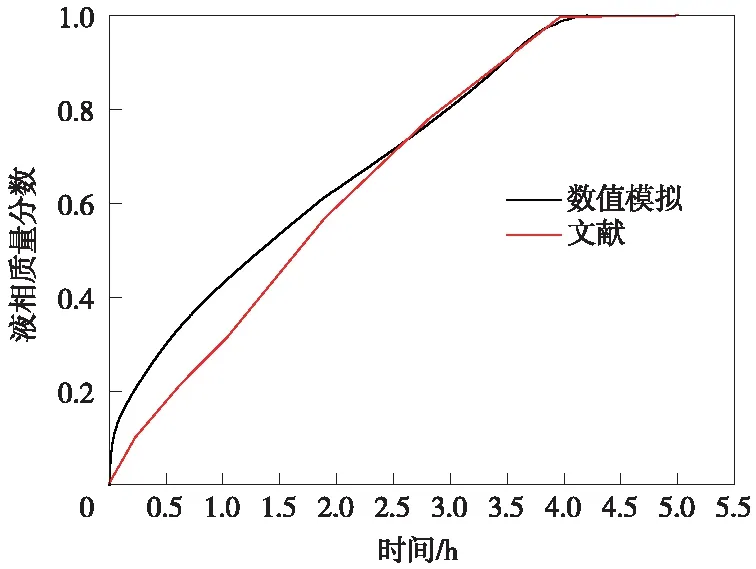
图3 PCM液相质量分数随时间变化对比图

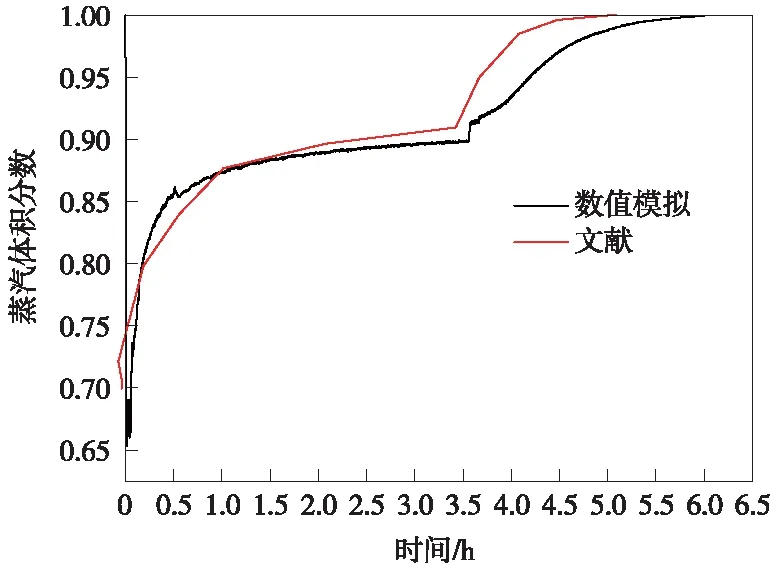
图4 出口蒸汽体积分数随时间变化对比图

3 计算结果及分析

3.1 不考虑自然对流对相变过程的影响

相变蓄热系统中PCM熔化前沿以及饱和蒸汽冷凝界面随时间变化云图如图5所示。管内的饱和蒸汽由于刚进入蓄热系统与低温PCM进行剧烈的热量交换，出口处的饱和蒸汽冷凝较多，贴近壁面处的饱和蒸汽首先进行冷凝，随着蓄热过程稳定之后，出口处的蒸汽体积分数趋于平稳，直到蓄热过程结束出口处全部为饱和蒸汽，因为没有考虑重力的影响，故只有环壁面处有一层冷凝水。

因为没有考虑到自然对流的影响，PCM的整个融化过程可近似为导热过程，从图5中可以看到，蓄热初始阶段，贴近高温壁面的PCM首先变为液态，并且由于出口蒸汽体积分数迅速降低产生大量的相变潜热使得出口端的PCM首先融化；随着蓄热过程逐渐稳定，管内冷凝水逐渐减少，PCM融化也趋于稳定，当PCM全部融化为液态后，PCM的温度将逐渐升高至与入口饱和蒸汽一样的温度将一部分显热存储起来，直到PCM全部达到入口饱和蒸汽温度后蓄热过程结束。

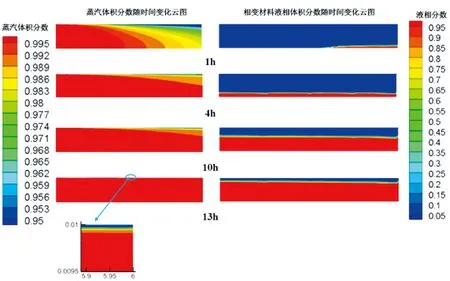
图5 不考虑自然对流时PCM液相质量分数及管内饱和蒸汽体积分数随时间变化云图

不考虑自然对流时PCM在蓄热过程中液相质量分数随时间变化曲线如图6所示。

图6 不考虑自然对流时管内相变材料的融化曲线

在不考虑相变材料的自然对流现象时可以将其简化为导热模型，由图6中可以看出，PCM的液相质量分数从0到1几乎是线性增加，当PCM的液相质量分数达到1时，代表所有PCM融化，进一步储存的热量为PCM的显热。

不考虑自然对流时蓄热过程出口蒸汽体积分数随时间变化曲线如图7所示。

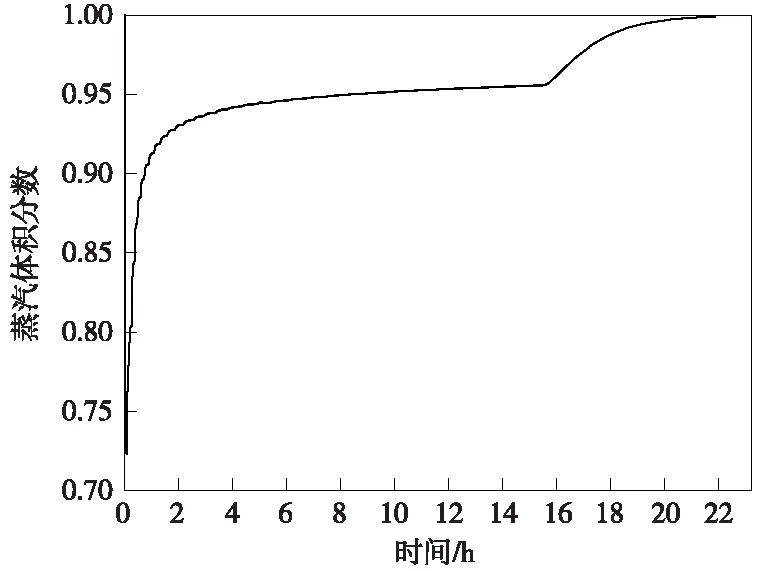
图7 不考虑自然对流时管外出口蒸汽体积分数随时间变化曲线

由图7中可以看出，蓄热初始阶段蓄热器换热剧烈，使得出口蒸汽质量迅速降低，随着蓄热过程逐渐稳定，管内冷凝水逐渐减少。因为蓄热器蓄热过程中相变材料的熔点是固定不变的，因此在蓄热稳定后出口蒸汽体积分数是几乎稳定不变的。在PCM完全融化后，PCM的温度会继续上升，直至与管内饱和蒸汽的入口温度一致，此段蓄热过程为显热蓄热。随着管外PCM的温度逐渐升高，管内出口蒸汽体积分数也随之升高，直至PCM与饱和蒸汽温度一致。出口蒸汽体积分数上升至1，管内全部为饱和蒸汽，不再与PCM发生换热，整个蓄热过程结束。

3.2 自然对流对相变过程的影响

自然对流的存在对于相变蓄热器中液态熔融盐的流动与传热过程影响十分巨大，为对比在数值模拟过程中是否考虑液态熔融盐自然对流现象的流动与传热差异，对考虑自然对流存在时熔盐融化过程中的流动与传热过程进行分析。蓄热时间为1.5 h时液相熔融盐的速度云图与温度云图如图8所示。

图8 蓄热时间为1.5 h时液相熔融盐的速度与温度云图

由图8(a)中可以看出，由于考虑自然对流的存在，在近壁面有液相熔融盐流动。由于靠近管壁的液相熔盐温度较高，在Boussinesq假设中，温度较高的熔融盐密度较小，所以熔融盐的运动方向与重力方向相反，沿X轴正方向运动。由图8(b)中可以看出，由于管内为高温的饱和蒸汽，导致近管壁面的熔融盐温度较高。由于液相熔融盐自然对流的存在，使液相熔融盐的温度场分布并不是平行的温度层，而是呈锥形的温度分布，而不考虑自然对流时液相熔盐温度分布为平行的温度层。因此，考虑自然对流情况的蓄热过程可以更快地进行。

为研究自然对流对相变材料融化过程的影响，对考虑自然对流存在与不考虑自然对流的情况进行了对比研究。不考虑自然对流与考虑自然对流存在情况下，融化时间在2 h时的液相分布图如图9所示。由图9(a)中可以看出，不考虑自然对流存在的液固两相区的相界面几乎是平行于轴线沿着径向移动，这是因为在不考虑自然对流存在的蓄热过程中，熔融盐的温度层为平行于轴线的温度层，且温度由内到外逐渐降低。并且管内饱和蒸汽流速大、行程短，导致内管进出口温差小。由图9(b)中可以看出，考虑自然对流存在时，熔融盐在融化过程中液固两相区的相界面不再是平行移动。熔融盐上端明显先行融化，固液相界面呈锥形状，并且随着蓄热过程的推进，固液接触面会越来越小，使得融化后期变得缓慢，尤其是蓄热末段，蓄热速率大幅降低。

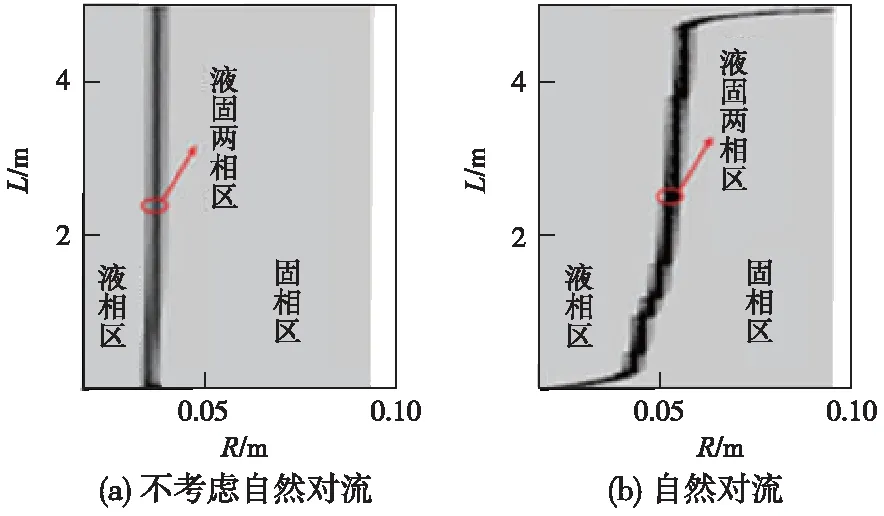
图9 自然对流与不考虑自然对流模型融化时间为2 h的液相分布图

2种模型液相分数随时间的变化情况如图10所示。由图10中可以看出，不考虑自然对流的情况下，蓄热过程中的传热主要为热传导，因此蓄热过程中PCM液相质量分数基本以不变斜率在上升；而考虑自然对流时总融化时间减少了30%，因为液相区域的传热还包括自然对流，加快了热传递。考虑自然对流模型在融化末段的蓄热速率相对缓慢，这是由于固液接触面积减少导致的。虽然不考虑自然对流的情况在蓄热末段的固液接触面积也逐渐减小，但是对不考虑自然对流的情况蓄热过程的影响可以忽略不计，而对考虑自然对流存在的影响较大。

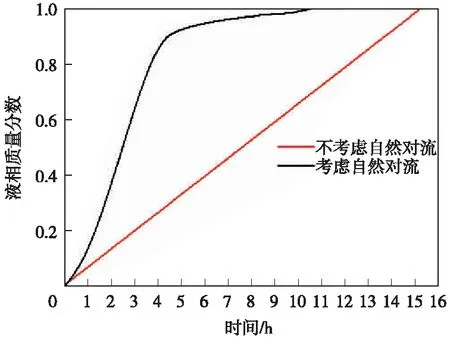
图10 2种模型液相质量分数随时间的变化

2种模型出口蒸汽体积分数随时间的变化情况如图11所示。

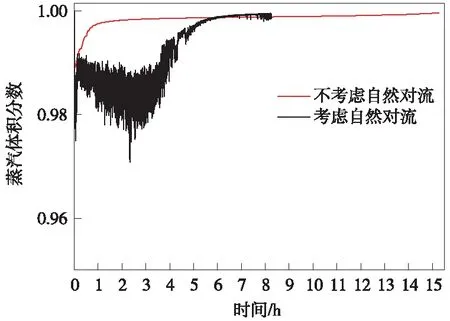
图11 2种模型出口蒸汽体积分数随时间的变化

从图11中可以看出，与不考虑自然对流的情况相比，自然对流在稳定蓄热阶段的管内蒸汽冷凝量更大，因此在蓄热过程中利用到蒸汽的相变潜热相对更多，这是导致考虑自然对流时比不考虑自然对流时的总融化时间减少了30%原因。考虑自然对流存在的情况在蓄热结束阶段相对缓慢，是由于管内蒸汽冷凝量大幅减少造成的；不考虑自然对流情况的管内饱和蒸汽冷凝量整体要比考虑自然对流存在小很多，这是其融化时间长的主要原因。

4 结论

构建了考虑自然对流的二维非稳态直接蒸汽相变蓄热器模型。其中，PCM区域基于焓-孔隙率法，HTF区域采用VOF模型与Lee模型结合的方法。对直接蒸汽相变蓄热器中的高温熔融盐熔化过程进行了数值模拟研究。主要结论如下：

(1)相对于不考虑自然对流的情况，考虑自然对流时液相熔融盐的自然对流现象会强化传热，主要因为在考虑自然对流时相变材料的固液接触面较大。更重要的是会增加管内饱和蒸汽的冷凝量，使熔化时间进一步缩短。同时，还详细分析了2种模型液相熔融盐以及管内饱和蒸汽的流动与传热情况。

(2)与不考虑自然对流的情况相比，考虑自然对流存在的液相熔盐固液接触面更大，使得融化更快的进行，蓄热时间缩短了30%。因此，在进行直接蒸汽相变蓄热器的数值模拟研究时，自然对流作用不可忽略。