上肢智能康复外骨骼的设计与仿真

马 泽，管小荣，李 仲，李 灿

(南京理工大学 机械工程学院， 南京 210094)

1 引言

调查显示，近年来脑卒中患病率逐年增高，且患者多伴有上肢功能康复障碍，而传统康复手段不能达到很好的治疗效果、康复成本较大，因此，构建一个能够适应人体上肢康复自由度，具有多种康复训练模式和科学评估模式，能够根据患者康复阶段自主调节康复训练规划的上肢智能康复外骨骼系统，对于上肢康复障碍患者具有重要意义。华盛顿大学研制了一款七自由度的上肢康复机器人CADEN-7，通过安装六维力传感器，实现基于轨迹跟踪的阻抗控制，通过肌电传感器获取肌电信号和运动意图，实现了被动、主动、半主动训练模式[1]。瑞士皇家理工大学开发的基于末端效应器的ARMIN系列机器人，已有三代产品，能够完成训练时速度、力等信息的采集，实现被动、主动康复训练模式[2]。华中科技大学设计的一款上肢康复机构，能完成被动模式、主动模式和肌电触发3种模式下摸嘴、摸头、摸左肩、摸右耳4组康复动作[3]。天津科技大学设计的一款基于力反馈加心率实时监测的双臂六自由度上肢康复系统，可完成被动、主动训练模式[4]等。由于目前多数康复外骨骼具有结构复杂、质量较大，美观和舒适性较差的缺点，因此，拟设计一款在满足康复主要需求前提下，结构简单、轻便，能适应不同人群，且美观、舒适性较好的上肢康复外骨骼结构，为拟设计的整体上肢康复外骨骼系统提供机械载体。本研究设计了一款能够满足康复系统要求上肢康复外骨骼结构，并对其进行了运动学、动力学分析，针对电机所受环境干扰及连续摩擦，进行了控制器的设计与仿真，来达到较好的跟踪精度。

2 机械结构设计

2.1 设计需求

人体解剖学研究显示，人体上肢是由多关节骨骼结构和复杂肌肉组织形成的综合体(见图1、图2)，主要包括3个部分：肩部、肘部和腕部，其中肩部运动主要包括肩关节前屈/后伸，外展/内收和内旋/外旋，共3个自由度；肘部运动主要有前屈/后伸和前臂内旋/外旋2个自由度；腕部包括前屈/后伸，外展/内收和内旋/外旋3个主要自由度。考虑到肘部、肩部2个大关节康复训练效果更明显和减小控制难度，取消了腕部康复自由度的设计。

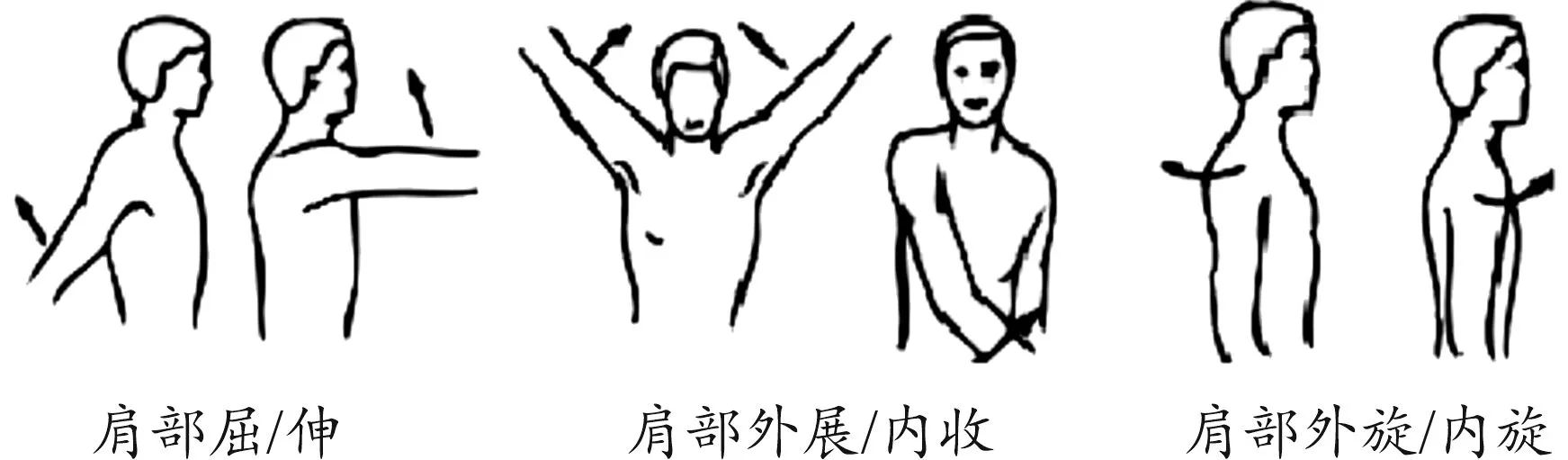
图1 肩关节运动示意图Fig.1 Shoulder’s movement

图2 肘关节及前臂运动示意图Fig.2 Elbow’s and forearm’s movement

2.2 长度调节

为适应不同人群的穿戴需求，外骨骼相关机构(大臂、小臂)的长度应该可以调节，使其具有一定的通用性，满足不同穿戴者的身材。依据成年男性18～60岁群体人体尺寸参数(见表1)，拟设计上臂调节长度在270～345 mm，前臂调节长度在200～260 mm，肩宽调节长度在330～420 mm。

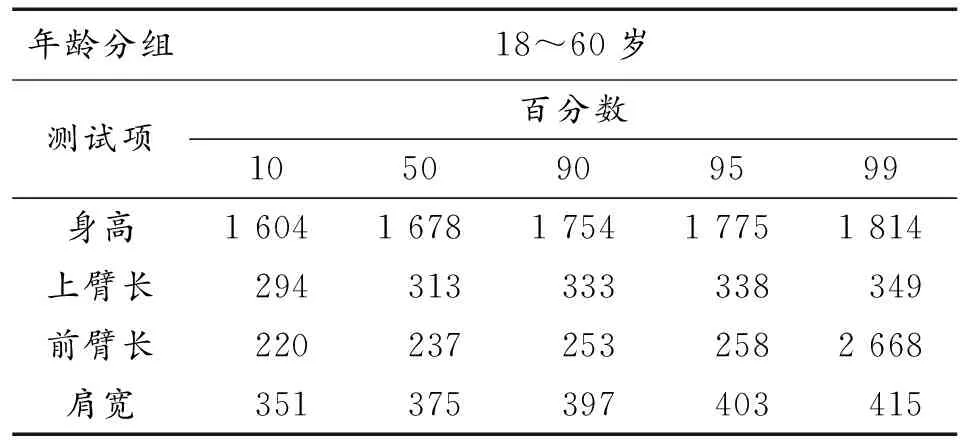
表1 GB 10000—1988中国成年人人体尺寸(mm)Table 1 GB 10000—1988 body size of Chinese adults

2.3 结构设计

整体结构如图3所示，结构设计主要遵从4个原则：自由度、通用性、舒适性和轻量化。

图3 整体结构示意图Fig.3 Overall structure

1) 自由度：结合患者群体主要康复需求与康复系统功能要求，设计的上肢康复外骨骼机器人具有4个自由度，前臂的内外旋、肘关节屈伸，肩关节屈伸、肩关节在一定角度下的外展内收和内外旋运动，驱动方面，前臂内外旋轴线在人体前臂内部，采用了电机驱动，齿轮传动的方式，其余3个自由度均使用电机直驱。

2) 通用性：依据2.2小节中长度调节中设计的参数，对结构整体进行设计，且由于所设计结果整体质量与力矩较小和为了实现更加灵活的尺寸调节，结构使用了使用螺栓拧紧的无级调节方式，来满足不同群体的康复需求。

3) 舒适性：考虑到病人训练过程中的舒适性与机械机构整体的美观性，大小臂结构部分均设计了护臂托持结构，该结构为传感器的安装提供了空间；结构整体设计了外壳与走线槽，并在患肢与结构接触处(手部、前臂、大臂)设置了安装绑带，保证人体手臂与外骨骼结构贴合的舒适性与运动同步性。

4) 轻量化：外壳采用塑料材料进行3D打印，主体结构材料使用7075铝合金，结构整体简单、质量较小。

3 运动学分析

3.1 D-H运动学分析

图4表示上肢康复外骨骼机械结构，针对所设计结构，简化模型(见图5)，采用传统D-H建模方法[5]，在所有杆构件上建立坐标系后，按照坐标运动顺序建立相邻两构件i-1与i之间的相对空间关系，即D-H坐标变换矩阵。

图4 上肢康复外骨骼机械结构示意图Fig.4 Mechanical structure of upper limb rehabilitation exoskeleton

图5 转动副关节连杆的D-H模型结构示意图Fig.5 D-H coordinates of rotating joint connecting rod

上述坐标运动都是相对于新坐标系的运动，因此连杆i关于i-1的坐标变换矩阵可用4个顺序右乘的齐次变换A矩阵表示，记Ai表示连杆i关于连杆i-1的坐标变换A矩阵，则，

Ai=Rot(z,θi)Trans(0,0,di)Trans(ai,0,0)Rot(x,αi)

(1)

将式(1)展开后，整理得：

(2)

其中，cosθi=cθi,sinθi=sθi,cosαi=cαi,sinαi=sαi，θi为关节变量，di，ai，αi为常量。

(3)

表2 D-H参数Table 1 D-H parameters

3.2 运动学逆解

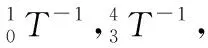
(4)

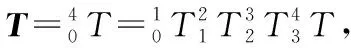
(5)

(6)

(7)

3.3 运动学验证

通过康复外骨骼完成康复动作的场景，定义康复外骨骼的初始关节变量和目标状态的关节变量，利用建立的D-H参数建立运动学模型，输入关节变量角度值即可得到模型姿态位置(图6)，反之，有对应的姿态位置，也可得到4个关节角度值，验证了所建立模型的正确性。

图6 外骨骼结构运动学简化模型示意图Fig.6 Simplified kinematics model of exoskeleton structure

3.4 运动空间分析

以图6模型位置为模型初始位置，根据患者的患侧训练需求，确定每个关节角度参数的变化范围(见表3)。基于蒙特卡洛法，利用随机函数生成各个关节变量变化范围的N(取N=1 000)个随机点，并把以上生成的所有关节变量随机值代入到所建立模型的位置向量中，得到设计结构的工作范围空间(见图7)，确定了康复机械臂末端能达到的点的集合，为后续生活动作(如：拿杯子，摸耳等动作)的轨迹规划提供设计依据[5-6]。

表3 各关节自由度运动范围Table 3 Motion range of each joint degree of freedom

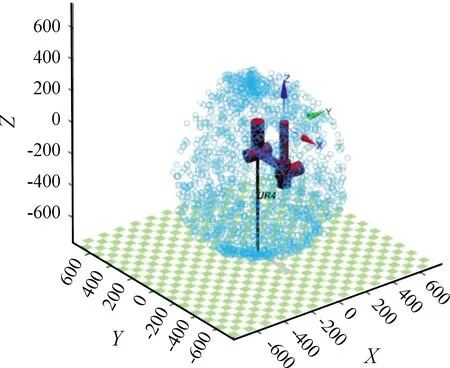
图7 康复机械结构示意图Fig.7 Working space diagram of rehabilitation mechanical structure

4 动力学分析

对所设计结构采用Kane方程法进行动力学分析。凯恩方程法适用于完整、非完整系统、开链及局部闭链系统等，其采用广义速度为独立变量，引入了偏速度、偏角速度、广义主动力、广义惯性力等概念，兼有矢量力学和分析力学的优点，若计算n=6(自由度)的同一种机器人，由表4可见Kane方程法在计算量和效率上的优势。但缺点表现在偏速度概念的物理意义含糊，建立起的动力学方程也不直观，偏速度的求解十分依赖每一个具体系统。综合来看，Kane方程法在动力学建模方面仍具有较大优势[7-8]。

表4 动力学建模方法运算量Table 4 Comparison of computational complexity of dynamic modeling methods

由于设计的是开链康复外骨骼机器臂，各关节自由度均为独立变量，故4个广义坐标即为每个自由度的旋转角度值，依次为qj=θj(j=1,2,3,4)，由图8可以看出，凯恩方程可描述为作用在系统上对应每个广义速度的广义主动力和广义惯性力的代数和为0，即，

图8 开链操作手凯恩方程法参数示意图Fig.8 parameter diagram of Kane equation method for open chain operator

(8)

预设重力加速度g，则基座运动的角速度、角加速度、线速度、线加速度为：

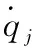
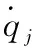
质心i点对广义速度的偏速度为：

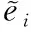
由于各个杆件均以转动副连接，则各杆件上速度、加速度递推算法如下：

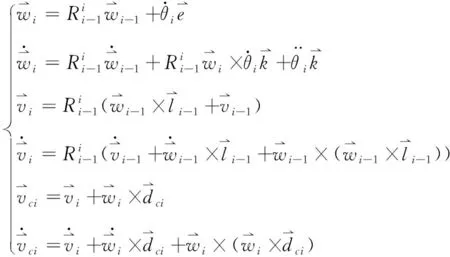
(9)

各杆件上的偏速度、偏角速度的递推公式为：

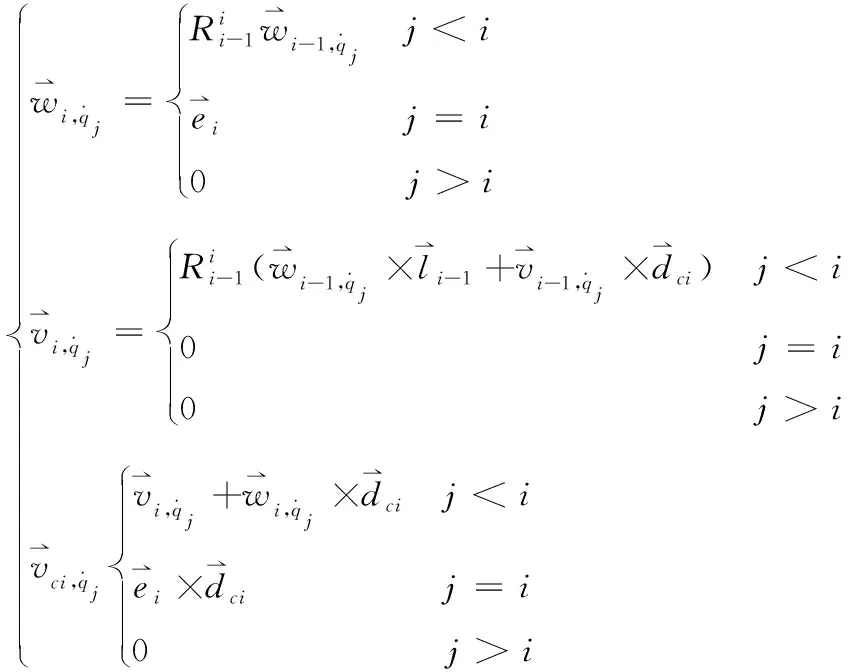
(10)

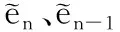
(11)

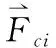
(12)

其中，

(13)

mi为杆件i的质量，集中于质心Ci；Ii为杆件i相对于质心Ci的惯性张量。

根据外骨骼机器人协助病人完成活动手臂康复动作的实际场景，控制目标是4个关节按照运动期望角度轨迹(见图9)运动，则可计算出动力学模型每个关节的理论力矩和Adams虚拟样机模型(见图10)下各关节的仿真力矩(见图11)，得到关节力矩曲线(见图12)。分析曲线结果，虽然仿真结果力矩曲线与实际计算的曲线结果有一定差异，但是在峰值与变化趋势上仍具有相似性，证明了动力学建模的正确性。根据力矩计算结果，选用相应关节的电机，该设计均采用国产脉塔智能电机。前臂内外旋关节使用RMD-L7015-23T型号电机，额定转矩为1 N·m，其余3个自由度使用RMD-X6-S2型号电机，额定转矩为18 N·m，所选电机具有CAN通信协议，驱动器与电机、减速器一体化，能满足控制与力矩需求。

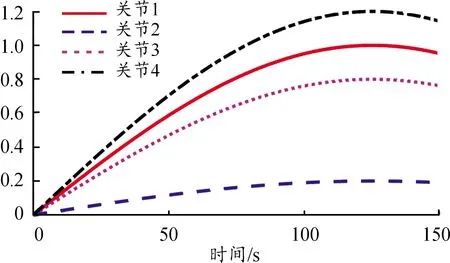
图9 各关节位置输入曲线Fig.9 Input curve of each joint position

图10 Adams虚拟样机模型示意图Fig.10 Simplified model of virtual prototype

图11 动力学模型各关节理论力矩曲线Fig.11 Theoretical torque curve of each joint of dynamic model

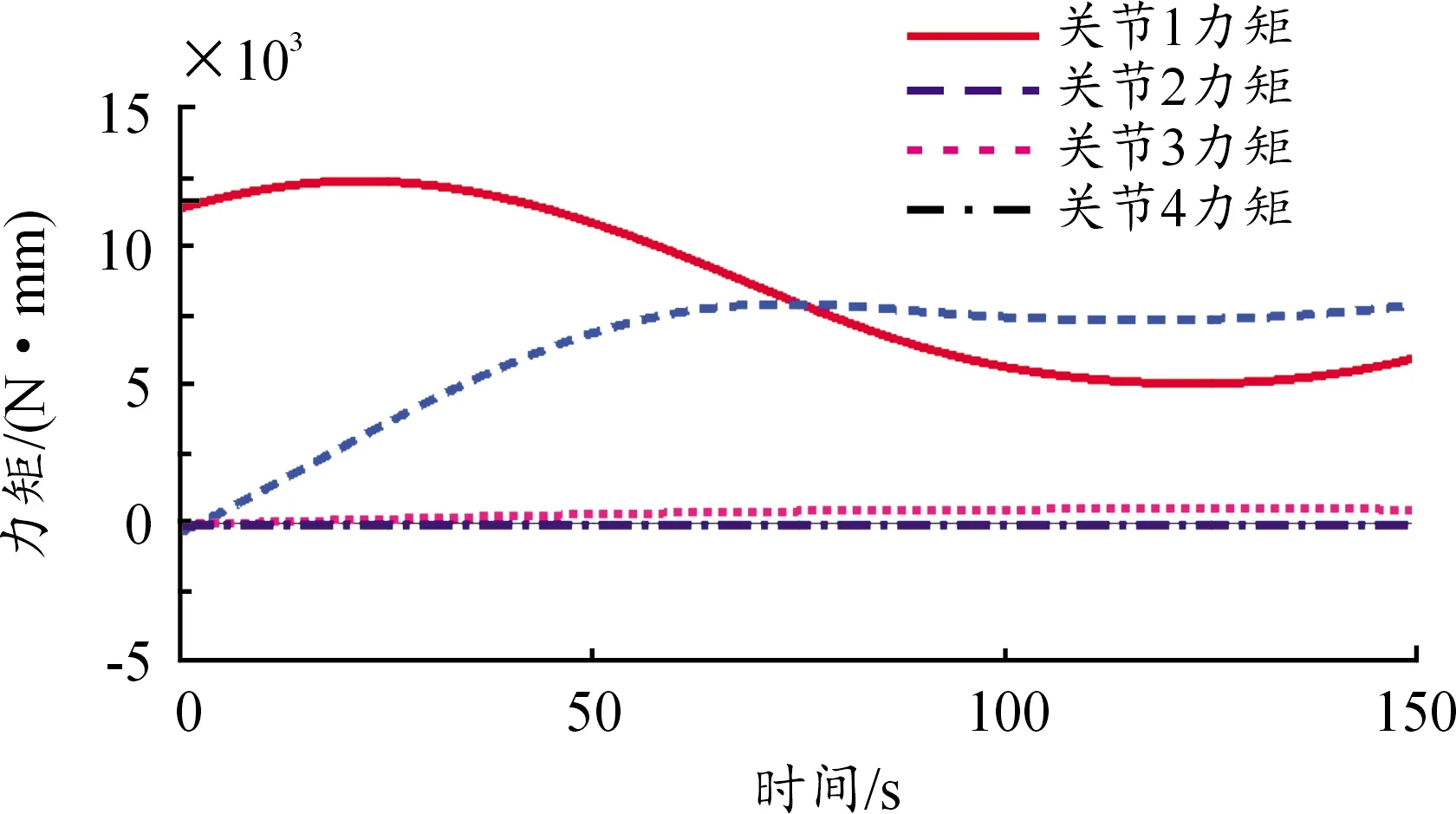
图12 Adams各关节仿真力矩曲线Fig.12 Simulation torque curve of Adams joints

5 控制器设计

对于同一个机器人，无论采用何种建模方法，机器人开链系统的动力学方程的一般形式可表示为：

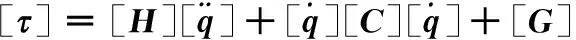
通过建立运动、动力学模型能够基于末端点确定每个关节电机需要转动到的角度及控制输入的力矩等参数，而实际运动中，会由于外界干扰及电机本身的影响存在不确定性，使得关节电机转动的理想角度与实际角度间存在偏差，因此，针对各电机，设计应用一种具有模糊自适应补偿的控制器，来减小偏差值，提高跟踪精度。

5.1 电机系统模型建立

所设计结构均采用无刷直流电机，其惯性载荷的运动动力学一般方程可由式(14)给出：

(14)

式中：m和y分别表示转动惯量和角位移；Ki是相对于输入电压单位的转矩常数；u为控制输入；B表示模型阻尼的组合系数。

考虑到电机运转过程中的连续摩擦及外界环境中的不确定性干扰，电机运转过程中的连续摩擦可由式(15)给出，建模不确定性及参数偏差效应可由式(16)给出，基于式(14)和式(15)，建立简化的参数模型(式(18))，式(17)为系统状态变量的设置和电机物理参数常数的标定值，由此，得到电机的系统模型(式(19))，联立可建立电机仿真模型

(15)

式中：a1和a2代表不同的摩擦水平；c1、c2和c3表示各种形状系数，以近似各种摩擦效应。

d(x,t)=-f(x,t)/Ki

(16)

(17)

(18)

(19)

5.2 模糊自适应符号积分鲁棒控制器设计

z1=x1-x1d表示输出跟踪误差，其中K1、K2、Kr是正反馈增益，通过模糊控制器，建立通用的模糊规则表，采用输出跟踪误差和其变化率作为输入，调节作为输出参数的K1、K2、Kr的值。ua作为前馈控制律，用于消除非线性摩擦效应并实现改进的模型补偿；us作为鲁棒控制律，其中us1用于稳定运动系统标称模型的线性鲁棒反馈律，us2用于衰减模型不确定性影响的非线性鲁棒项[9]。

(20)

由式(20)建立符号积分鲁棒控制器系统模型，进而得到基于模糊自适应的符号积分鲁棒控制器的电机系统整体仿真模型(见图13)。

图13 系统整体仿真模型示意图Fig.13 Overall system simulation model

将期望角度值曲线函数输入系统中，得到仿真轨迹的曲线及理想与实际角度的偏差曲线，与普通PID控制器控制效果比较：PID控制在偏差达到10-3级别，再提高P增益，修改I、D参数，容易出现失稳状况，相较而言，所设计应用的符号积分鲁棒控制器，更容易得到较好的增益参数(图14)，来达到更好的轨迹跟踪控制效果，减小控制偏差。

图14 符号积分鲁棒控制器与PID控制器增益参数曲线Fig.14 Control effect diagram of symbolic integral robust controller and PID controller

6 结论

1)设计了满足康复系统要求的上肢康复外骨骼结构。基于D-H法，对设计模型进行了正逆运动学分析，得到了其运动范围空间；基于凯恩方程法进行了动力学分析，并通过Adams仿真验证了该方法的正确性与可行性，并根据所得到的各关节理论计算力矩进行电机选型。

2) 考虑电机模型的连续摩擦与实际场景中不确定性的干扰，进行了控制器的应用设计与仿真，用模糊方法取得了更好的控制参数，减小了跟踪误差，验证了模型的先进性与可行性，为控制器的参数选择提供了科学依据，对实现更高精度的控制具有重要意义。

3) 所做工作满足了搭建整体系统的前期需求，为模拟设计的完整上肢智能康复系统进行了理论准备，对其他串联机械臂的研究具有参考价值。

4) 结构外形曲线和长度调节机构仍可改进，后续传感器及走线在实际测试后，可以进行更加科学合理规划；动力学方法虽计算效率较高，但引入的一些变量实际物理意义模糊；控制器在实际应用中仍需要进一步测试以获得优异的参数值。