基于GLCT和FPO的时变工况行星齿轮箱故障特征提取*
孙斌 李宏坤 刘艾强 张孔亮
(大连理工大学机械工程学院)
0 引言
行星齿轮箱在工业应用广泛,如风力发电,航天航空等[1]。行星齿轮箱作为旋转机械的主要传动部件,长期工作在冲击、交变载荷和工况大幅度变化的情况下,其关键零部件如齿轮,极易发生故障,从而引起巨大的经济损失和恶性事故[2-3]。因此,对行星齿轮箱的齿轮故障诊断具有重大的经济与安全意义。
行星齿轮箱在变转速工况下,所测得的振动信号具有典型的非平稳和非线性特点。如果利用传统的信号处理方法,如快速傅里叶变化,得到的频谱模糊,无法获得故障特征频率,难以识别变转速下的齿轮故障[4]。
时变转速下对行星齿轮箱的故障诊断,阶次跟踪被认为是最有效的工具之一[5]。在阶次跟踪中,原始信号以恒定的角度间隔重新被采样,原始的时域非平稳信号转化为角域的平稳信号。阶次跟踪的方法可以消除由于转速的变化带来的频谱模糊的现象,在传统的阶次跟踪中,需要安装硬件设备获得转速信息用于信号的重采样。但是,由于空间和成本有限,安装硬件设备在很多场合都难以实现[6]。
为了克服上述问题,从振动信号的时频表示中提取到瞬时速度信息是比较常用和节约成本的方法。但是,时频聚集性对所要提取的瞬时速度精度影响较大。许多学者将短时傅里叶变换(STFT)和连续小波变换(CWT)的传统时频分析方法,应用于机械故障诊断领域。虽然这些传统的时频方法能够处理非平稳信号,但是受海森堡(Heisenberg)不确定性原理的限制,时间和频率分辨率不能同时达到最佳,同时也对噪声比较敏感[7]。此外,由于所测得行星齿轮箱的信号是典型的调制信号,使用传统的时频分析会出现能量混叠和时频脊线模糊,导致难以准确提取到转频信息[8]。为了提高时频聚集性,I Daubechies 等提出了同步压缩变换(SST),利用时频重排的方法,获得了聚集性良好的时频表示[9]。Gang Yu等人提出了同步提取变换(SET),与SST的压缩方式不同,只保留与时变特征最相关的时频信息,大大提高了时频的能量聚集性[10]。但是上述时频分析方法存在对噪声敏感,不能很好的表征非线性特征的多分量信号的问题。本文运用一种新型的时频分析方法,广义线性调频小波变换(GLCT),可以克服现有时频方法的一些缺陷,并且对噪声不敏感[11]。
从时频表示中,提取到转频曲线是无转速阶次分析中不可或缺的一部分。Zhao等使用峰值搜索算法从时频图中提取瞬时频率,实现了变转速下轴承的故障诊断[12]。陈剑等人提出一种改进的Crazy Cliber算法,从STFT 时频脊线提取脊线,并成功实现了变转速下的轴承故障特征提取[13]。但是,峰值搜索算法和Crazy Cliber算法容易陷入局部最优,考虑不到整个信号的轮廓,如果选择不合适的起点,提取到的瞬时频率将会是错误的,而且这种方法在低信噪比中是无效的[14]。
针对上述存在时频聚集性不高和提取到的瞬时频率准确性低的问题,本文提出了一种基于GLCT和FPO相结合的方法,用于诊断在时变转速下行星齿轮箱齿轮的故障。采用GLCT对振动信号进行时频表示,该时频方法比传统的时频分析方法如STFT,时频聚集性高,并且对噪声不敏感;再采用FPO 从时频矩阵中提取瞬时速度信息,该提取算法克服了峰值搜索算法的噪声干扰和局部最优[15],然后利用所提取到的瞬时速度信息进行信号重采样,得到角域平稳信号,再进行包络阶次分析,得到故障特征阶次,达到故障诊断的目的。仿真和实验的振动信号证明了该方法在变转速运行下行星齿轮箱齿轮故障诊断的有效性。
1 基本原理介绍
1.1 广义线性调频小波变换(GLCT)
标准的短时傅里叶变换(STFT)如式(1):

将引进一个解调因子,去消除调制成分的影响。考虑到调制成分是随着时间变化的,所以引入的解调因子也必须是时变的。引入时变的解调因子s(t) 的STFT表达式为:
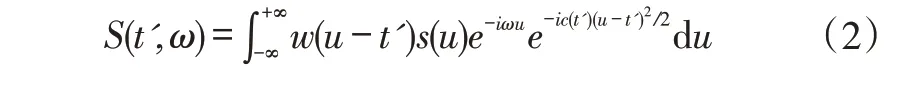
s(t)的STFT幅值用瞬时频率φ(t')可以表达为:
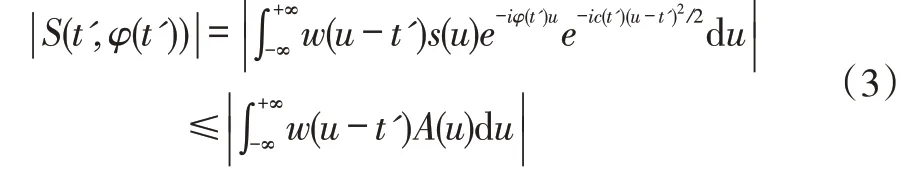
从上式可以看出,如果解调因子和分析信号的调制成分相一致,则瞬时频率φ(t')的STFT 幅值达到最大,然后时频能量在瞬时频率处具有很高的聚集性。但是在大多数情况下,一个信号的IF 特征不能预先得知,则解调因子e-ic(t')(u-t')2/2难以准确确定,特别是含有复杂的多成分信号中,更加困难。为了解决上述问题,用离散的解调因子无限去逼近最优的解调因子e-ic(t')(u-t')2/2,则用离散化的解调因子表示STFT 的公式如式(4):
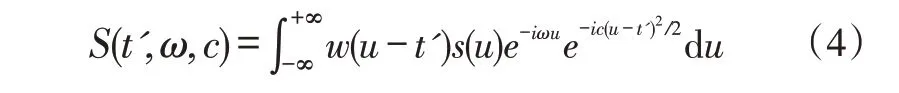
如果离散的解调因子与信号的调制成分相近时,则在时频表示中,瞬时频率的时频点(t',ω)有很高的能量聚集,则|S(t',ω,c) |幅值达到最大值。从而能够得到最佳的参数c为:
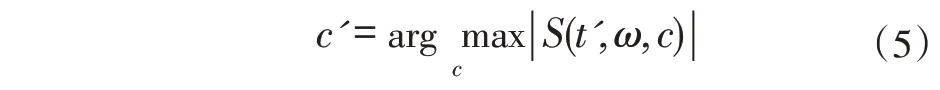
则时频表达式为:

频谱的定义式为:

为了得到最优的解调因子e-ic(t')(u-t')2/2,引入参数α,通过旋转arctan(-c),对时频结果产生影响,则时频平面旋转为:
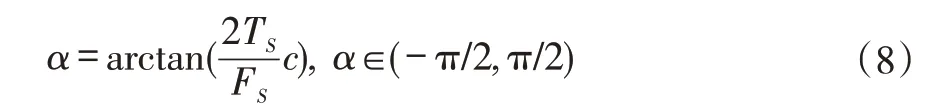
则上述的时频表达为:

因为参数α有N个值,则时频平面能均分N+1 个部分:

由上述可知,GLCT比STFT多引入了一个参数N,如果N=1时,GLCT即为STFT。
1.2 快速路径最优算法(FPO)
经过上述GLCT 得到的时频结果为GS(t',ω),计算时频表示中每个时刻幅值的局部极大值,然后得到该时刻所有极大值所对应的频率值为:

其中,tn(n=1,2,...,N)表示时频表示的时刻点;Np(tn)表示时刻tn的局部极大值的个数;fm(tn)是时刻tn处第m个极值所对应的频率值,其幅值的大小记为SPm(tn)。
采用FPO 确定每个时刻点处应该被提取出来的幅值极大值,极大值所对应的频率连接起来即为目标脊线,具体算法如下:

其中,mc(tn)为时刻tn应该被提取的幅值极大值;[F]表示优化方程,该方程的解就是目标脊线。优化方程为:
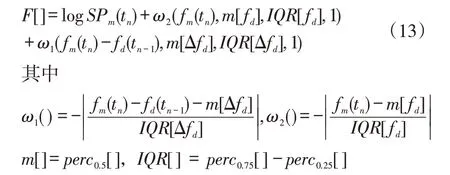
其中,Δfd是fd的导数;percp[f(t)]表示f(t) 的第p分位数。则优化方程的解为:
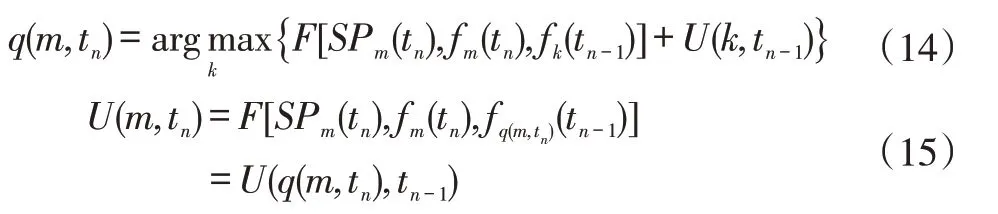
其中,n=1,2,...,N,m=1,2,...,Np(tn),q(m,tn)确定每个时刻幅值的极大值与前一时刻哪一个极值点构成优化路径,规划所有路径的可能性。U(m,tn)表示优化结果的中间向量,选择该时刻U(m,tn)最大值的幅值极大值点对应的频率值作为目标脊线。
2 提取方法流程
为解决时变工况下无转速信号和传统时频方法时频聚集性不高导致提取的瞬时转速误差较大的问题,提出了基于GLCT 和FPO 的时变转速行星齿轮箱故障诊断方法。所提方法的流程图如图1,具体实施步骤如下:

图1 所提方法流程图Fig.1 The flowchart of proposed method
步骤1:采集时变转速下行星齿轮箱的振动信号。
步骤2:对获取的振动信号进行GLCT 时频表示GS(t',ω)。
步骤3:设置最大搜索频率,在GS(t',ω)时频域中采用FPO算法提取瞬时转频趋势线。
步骤4:采用最小二乘法对提取的趋势线进行拟合,得到目标脊线;进而利用提取的转速曲线对原始振动信号进行等角度重采样,将非平稳信号转换为角域平稳信号。
步骤5:对角域信号进行包络阶次分析,从包络阶次谱中提取故障特征阶次并判断故障类型。
3 仿真验证
为了证明上述方法的有效性,仿真一个如下时变转速下的太阳轮故障信号:
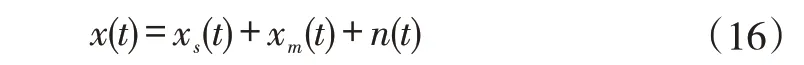
其中,xs(t)为轴的振动信号;xm(t)为太阳轮局部故障振动信号;n(t)为高斯白噪声,具体数学模型如式(17)和(18):
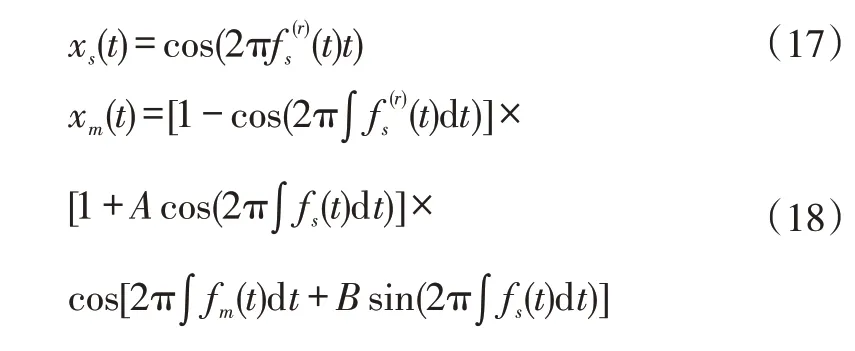
式中,(t)为轴旋转频率;fs(t)为太阳轮故障特征频率;fm(t)为齿轮啮合频率。
考虑到时变转速,则上述表达式为:

在这个仿真信号中,采样频率Fs=1024Hz,采样时间为10 秒,n(t)=-5dB。而仿真信号中,太阳轮故障阶次Os为:
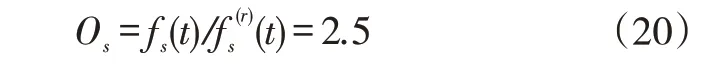
上述仿真信号的时域波形及其FFT 频谱和包络谱如图2所示。由图2可知,故障冲击被完全淹没在噪声中,此外受时变转速影响,故障特征频率以及调制成分在频谱图中出现混叠和模糊现象,从而不能提取到有用的故障特征信息。

图2 仿真信号时域图及其相关谱图Fig.2 Time-domain diagram of simulated signal and its related spectrum diagram
图3 为本文所提方法的分析结果,图3(a)为仿真信号GLCT时频表示,瞬时频率最低的时频脊线为理论转频曲线。因此,以瞬时频率最低的时频脊线为基频O即为所提取的目标脊线,进行角度重采样。用FPO从图3(a)的时频表示中提取到的目标脊线如图3(b)的黑色曲线所示,因所提取的目标脊线不够光滑,本文采用最小二乘法进行曲线拟合,图3(b)的蓝色线为拟合曲线,红色线为理论曲线。从图3(b)可以明显看出拟合后的曲线和理论曲线基本重合。根据上述提取出来的曲线进行角度重采样包络阶次谱,从图中可以明显得到O,Os-O,Os,Os+O,2Os。从上述的分析结果可以得出本文所提出的方法能够准确提取到变转速下仿真信号的太阳轮故障特征。
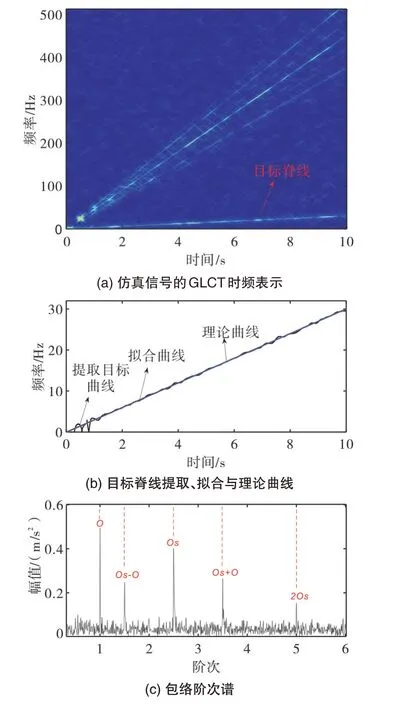
图3 本文所提方法分析结果Fig.3 The analysis result of the method proposed in this article
为了验证本文所提方法的优越性,分别采用STFT与FPO 和GLCT 与峰值搜索算法进行对比。仿真信号的STFT时频表示如图4(a)所示,用FPO从图4(a)中提取到的目标脊线如图4(b)黑色曲线所示,红色线为最小二乘拟合曲线,蓝色线为理论曲线,使用拟合后的曲线得到的包络阶次谱如图4(c)所示。可以看出,由于所采用的时频分析方法时频聚集性不高,并且对噪声比较敏感,导致提取出来的目标脊线与理论曲线误差较大,进而最后的诊断效果不理想。

图4 STFT与FPO分析结果Fig.4 STFT and FPO analysis results
从图5可以看出,由于峰值搜索算法考虑不到时频矩阵的全局信息,容易出现局部最优的现象,导致所提取到的目标曲线与理论曲线误差较大,最后的诊断效果不理想。
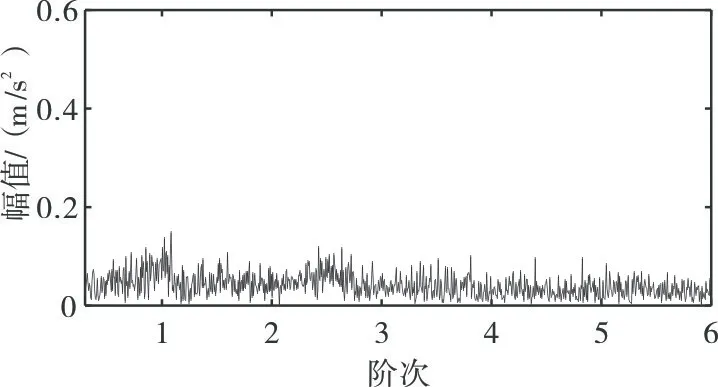
图5 GLCT与峰值搜索算法结果包络阶次谱Fig.5 GLCT and peak search analysis results envelope order spectrum
综上,本文所提出的方法,能克服传统时频分析方法的时频聚集性不高,而带来的目标脊线提取精度不高以及传统的时频脊线提取算法由于考虑不到时频矩阵的全局信息,导致提取到的目标脊线局部最优的问题,最后能够准确提取时变转速下太阳轮故障特征,从而验证了本文所提的方法在时变转速下对行星齿轮箱齿轮故障特征提取的有效性。
4 实验验证
4.1 实验说明
设计了行星齿轮箱太阳轮和行星轮故障在时变转速下的模拟实验,实验系统如图6 所示,采集实验是在图6所示的实验台上进行的,主要由变频器、驱动电机、行星齿轮箱、磁粉制动器、转速传感器、加速度传感器(型号为美国DYTRAN 公司生产的3035B 型传感器)和安装NI9234采集卡的工控机组成。

图6 时变转速下行星齿轮箱实验系统Fig.6 Planetary gearbox experimental system under time-varying speed
在本实验中,行星齿轮箱的齿圈固定,太阳轮为输入端,行星架为输出端,电机的转速在20s内从0~1800r/min线性增加,为了验证提取到的目标脊线的准确度,以转速传感器测得的瞬时转速为理论转速。采样频率为12800Hz,为了增加分析的可靠性,本文取5~15秒的数据。磁粉制动器施加的扭矩为0,行星齿轮箱的参数见表1。为了模拟行星齿轮箱齿轮的局部故障,通过线切割技术在太阳轮的某个轮齿上切割一部分和切掉行星轮一个轮齿,这样形成太阳轮断齿和行星轮缺齿局部故障,故障齿轮如图7所示。行星齿轮箱的故障特征阶次见表2。

表1 行星齿轮箱的参数Tab.1 Parameters of planetary gearbox

图7 齿轮故障件Fig.7 Gear failure parts

表2 行星齿轮箱各部分故障特征阶次Tab.2 Characteristic order of failure of each part of planetary gearbox
4.2 实验验证1:太阳轮故障信号分析
太阳轮缺齿故障振动信号的时域波形及其对应的傅里叶频谱和包络谱如图8所示。可以看到,随着转速的升高,冲击逐渐变大;同时,受时变转速影响,谱图中会出现频谱模糊现象,因此根据传统的时频分析很难提取到有价值的故障特征信息。
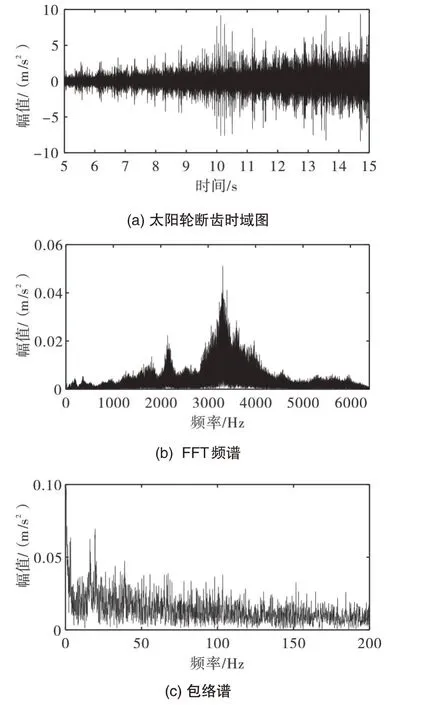
图8 太阳轮断齿时域图及其相关谱图Fig.8 Time domain diagram of sun gear broken tooth and its related spectrum diagram
为提升运算效率,本文对原始信号进行降采样预处理,降采样的频率设置为512Hz。图9(a)为降采样信号GLCT 时频表示,从图中可以明显的看出来,瞬时频率最低的时频脊线为太阳轮输入端的瞬时速度曲线,即目标提取脊线。用FPO 从图9(a)提取到的目标瞬时频率脊线如图9(b)的黑色曲线所示,本文采用最小二乘法拟合所提取出来的目标曲线为图9(b)的红色曲线,蓝色线为理论曲线,从图中可以看出拟合后的曲线和理论转频曲线基本重合。根据上述所拟合后的曲线进行角度重采样后的包络阶次谱如图9(d)所示,可以清晰地观察到O,Os-O,Os,Os+O,2Os,2O的故障特征信息。上述分析结果表明太阳轮出现故障,从而验证了所提算法的有效性。

图9 本文所提方法分析结果Fig.9 The analysis result of the method proposed in this article
为了验证本文所提方法的优越性,分别采用STFT 与FPO 和GLCT 与峰值搜索算法进行对比。图10(a)为太阳轮断齿信号的STFT 时频表示,用FPO 从STFT 时频表示中提取到的目标脊线如图10(b)的黑色曲线所示,红色线为拟合曲线,蓝色线为理论曲线,使用拟合曲线得到的包络阶次谱如图10(c)所示。从最后的诊断结果可以看出,所采用的时频分析方法时频聚集性不高,并且对噪声敏感,导致提取出来的目标曲线与理论的曲线误差较大,进而最后的诊断效果不理想。
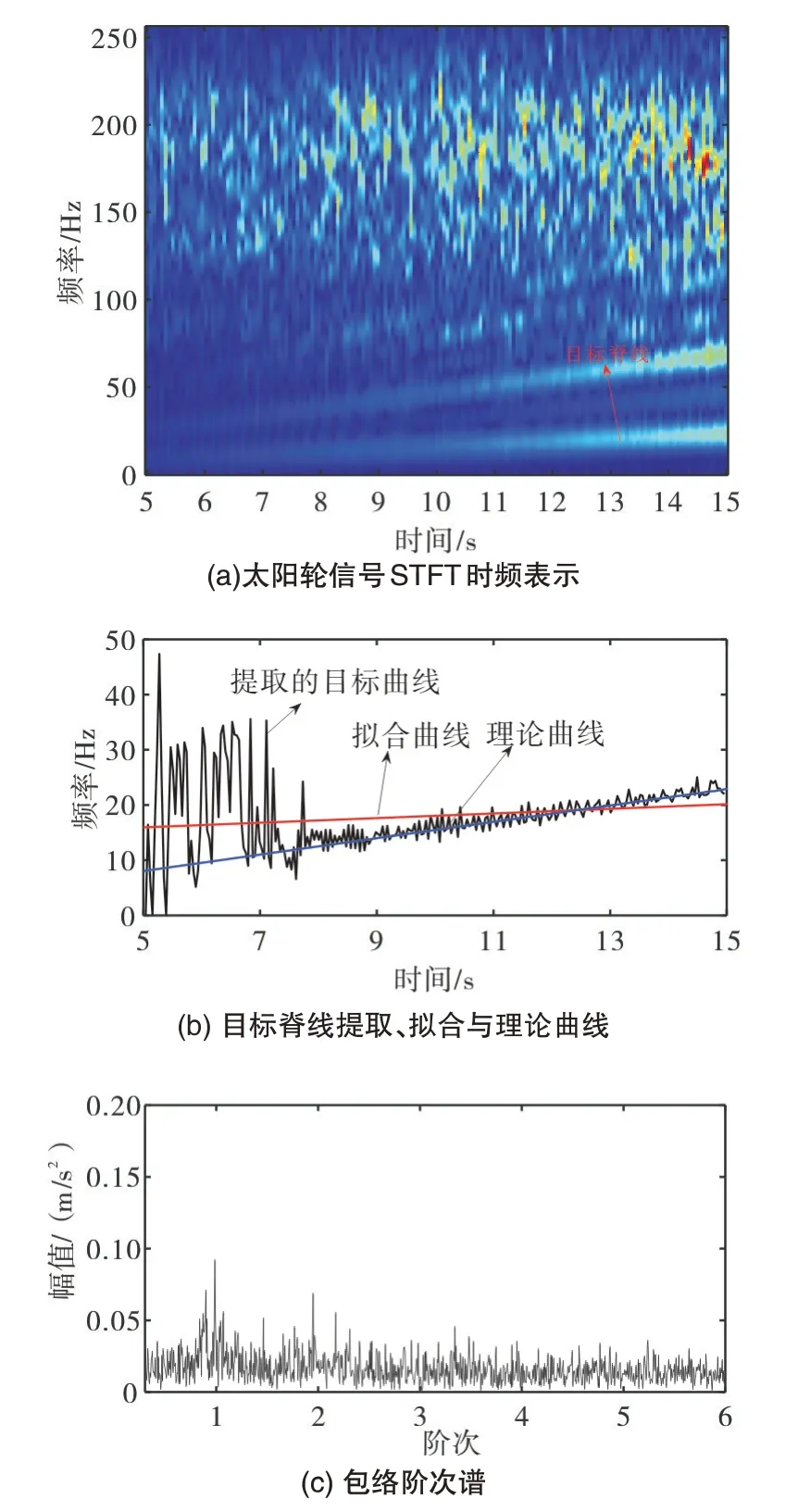
图10 STFT与FPO分析结果Fig.10 STFT and FPO analysis results
GLCT 和峰值搜索的包络阶次谱如图11 所示。可以看出,从最后诊断结果可以看出,因为峰值搜索算法一旦出现选错频率起始点,将导致所提取到的目标曲线错误,从而使该方法失效。
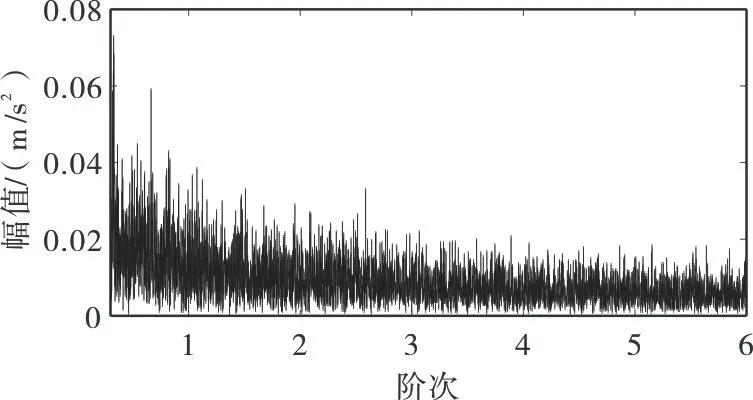
图11 GLCT与峰值搜索算法结果包络阶次谱Fig.11 GLCT and peak search analysis results envelope order spectrum
4.3 实验验证2:行星轮故障信号分析
行星轮缺齿故障振动信号的时域波形及其对应的傅里叶频谱和包络谱如图12 所示。可以看到,随着转速的升高,冲击逐渐变大;同时,受时变转速影响,谱图中会出现频谱模糊现象,因此根据传统的时频分析很难提取到有价值的故障特征信息。

图12 行星轮缺齿时域图及其相关谱图Fig.12 Time domain diagram of planetary gear missing teeth and its related spectrum diagram
图13(a)为降采样信号GLCT时频表示,从图13(a)可以明显的看出来,瞬时频率最低的时频脊线为目标提取脊线。用FPO从图13(a)提取到的目标脊线如图13(b)黑色曲线所示,红色线为拟合后的曲线,蓝色线为理论曲线,从图中可以看出拟合后的曲线和理论转频曲线基本重合。根据上述所拟合后的曲线进行角度重采样,最后的包络阶次谱如图13(d)所示,可以明显得到O,Op-Oc,Op,Op+Oc,2Op,2O,4Op的故障信息。上述分析结果表明行星齿轮出现故障,从而验证了所提算法的有效性。

图13 本文所提方法分析结果Fig.13 The analysis result of the method proposed in this article
为了验证本文所提方法的优越性,分别采用STFT与FPO 和GLCT 与峰值搜索算法进行对比。行星轮缺齿信号的STFT时频表示如图14(a)所示,用FPO从图14(a)中提取到的目标曲线如图14(b)黑色曲线所示,红色线为拟合曲线,蓝色线为理论曲线,使用拟合曲线得到最后的包络阶次谱如图14(c)所示。从最后的诊断结果可以看出,因为所采用的时频分析方法时频聚集性不高,并且对噪声敏感,导致提取出来的时频曲线与理论的时频曲线误差较大,导致最后的诊断效果不理想。


图14 STFT与FPO分析结果Fig.14 STFT and FPO analysis results
GLCT和峰值搜索的包络阶次谱如图15所示。从最后诊断结果可以看出,峰值搜索算法一旦选错频率起始点,将导致所提取到的目标曲线错误,从而使该方法失效。
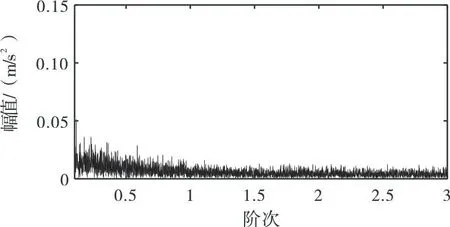
图15 GLCT与峰值搜索算法结果包络阶次谱Fig.15 GLCT and peak search analysis results envelope order spectrum
综上,本文提出的方法,能在强噪声的背景下和时变转速工况下,准确提取到行星轮缺齿故障信息。提出的GLCT方法能够生成时频聚集性较高的时频图,克服了传统的时频方法在强噪声背景下时频聚集性不高的问题。提出的FPO脊线提取算法能够考虑时频矩阵的全局信息,准确提取到目标脊线,克服了传统脊线提取算法容易陷入局部最优的问题。
5 结论
针对无转速计时变工况下行星齿轮箱故障特征难以提取的问题,提出了基于GLCT与FPO的故障特征提取算法。通过构造仿真信号和实际应用对其有效性和优越性进行分析,可以得到如下结论:
1)在噪声干扰比较严重的情况下,GLCT的时频聚集性和噪声鲁棒性优于传统的STFT 方法,从而可以清晰地展现齿轮箱瞬时频率曲线,为后续目标脊线提取提供基础。
2)FPO时频脊线搜索算法能够考虑到时频矩阵的全局信息,提取到的时变转速曲线与理论曲线能够完全重合,克服了峰值搜索算法容易陷入局部最优和提取目标脊线不准确的问题。
3)该算法能在不安装转速计等硬件的条件下提取转速曲线,随后对原始振动信号进行角域重采样,在其包络阶次谱中能够准确识别到行星齿轮箱故障特征阶次,为变转速工况下的行星齿轮箱故障诊断提供了一种新思路。

