巧构距离模型解题

浙江省嘉善第二高级中学 (314100) 鲁和平

距离是一个非常重要的几何量.在高中数学里，学生共学过三个距离公式:两点间的距离公式；平行直线之间的距离公式；点到直线的距离公式.如果我们把这三个距离公式，看作三个解题的思维模型，就可以按图索骥，解题思路也随之油然而生.

由于很多代数式的结构与两点间的距离公式有着惊人的相似之处，我们就可以运用配方法，调整各个坐标的符号，配凑成两点间的距离公式模型，再充分挖掘其几何特征，即可求解.

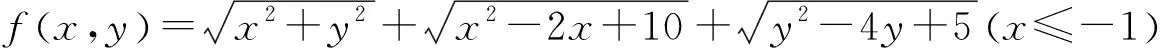
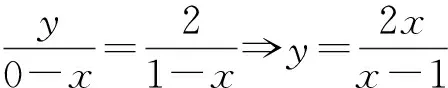
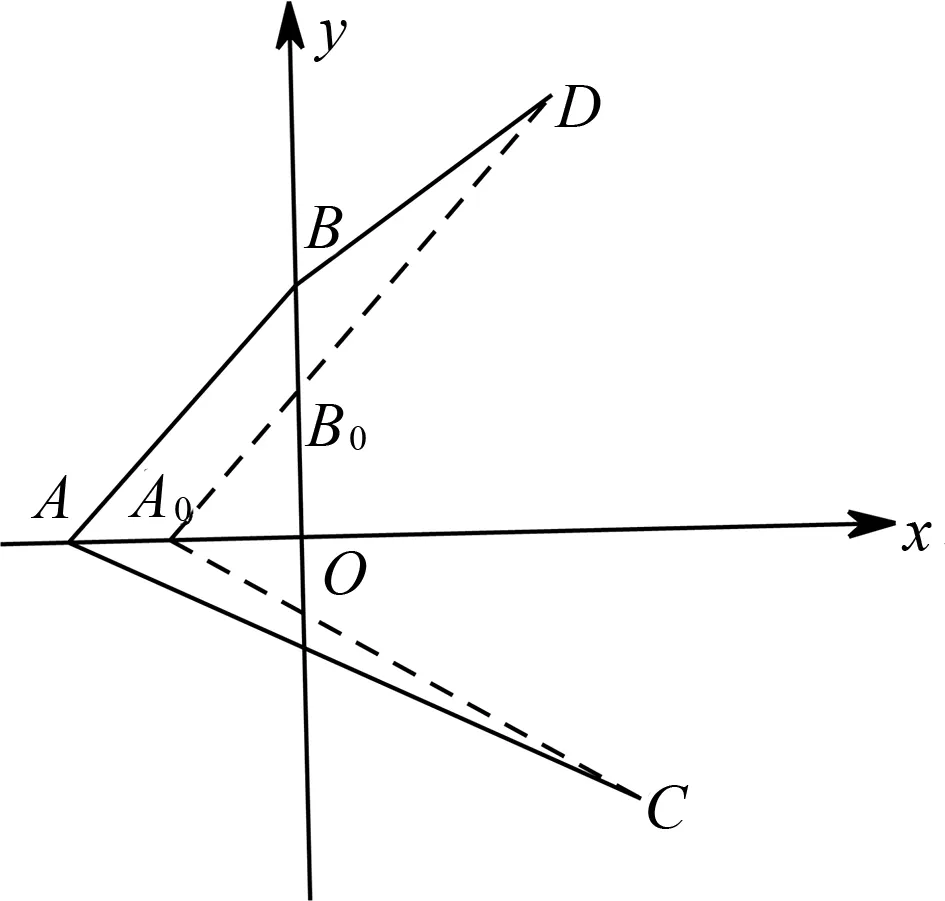
图1

评注：本题的关键在于将三点A,B,D调整为共线，这样点A固定，|AC|亦固定，二元函数的最小值就确定了.

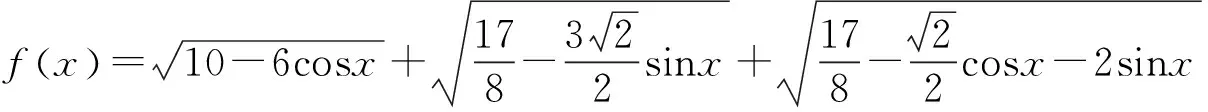
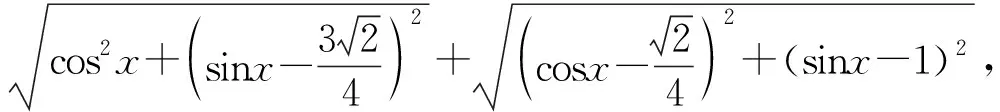
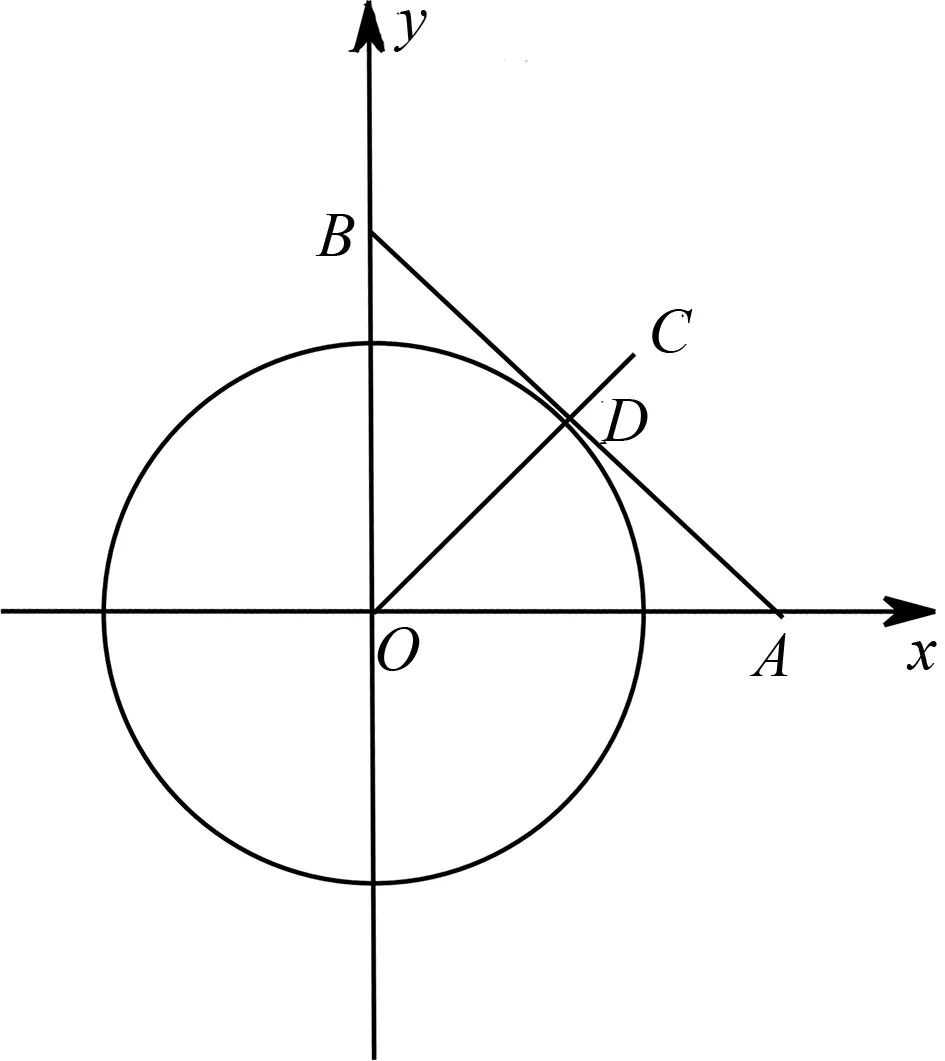
图2

评注：本题结构式较为复杂，由于含有sinx,cosx自然就会联想到单位圆.通过计算斜率，发现O,D,C三点共线，最后论证当点P与点D重合时，f(x)=f(θ)=|PA|+|PB|+|PC|才能取得最小值，对直觉思维的要求很高.

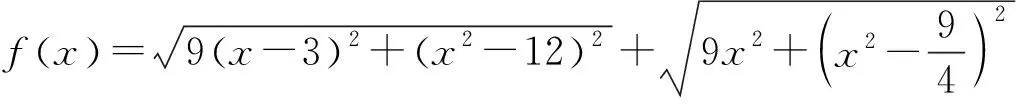
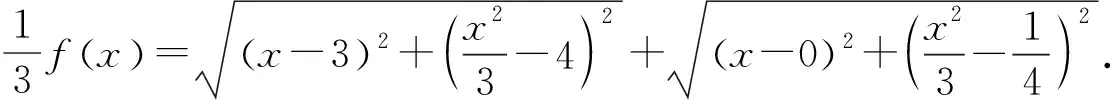
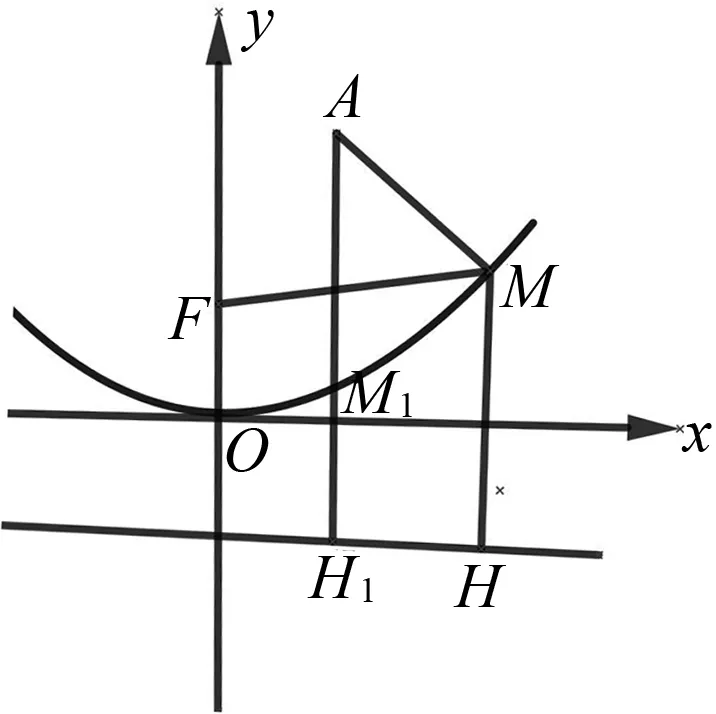
图3

评注：对函数表达式结构进行一系列改造，转化为抛物线上的动点M，到定点A及焦点F的距离之和，利用抛物线的几何性质，问题就迎刃而解.

例4 求函数y=x4-12x3+68x2-192x+832的最小值.

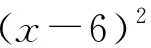
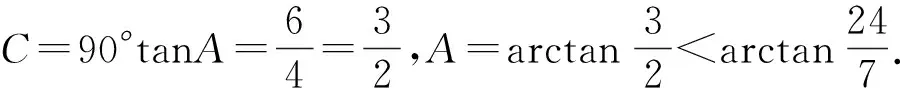
评注：先对函数解析式通过因式分解、配方才能发现它与两点间距离公式的异曲同工之处.将两距离之积转化为三角形面积问题，也是思维上的重大飞跃.用三角法求出sinA的最大值，也是本题的一大难点.

由于两平行直线之间的距离公式，是由两点间的距离公式导出的.所以很多结构式，貌似两点间的距离公式的模型，实则可以转化为两平行直线之间的距离公式的模型求解.

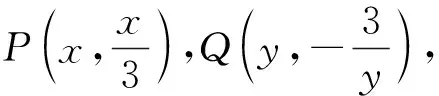
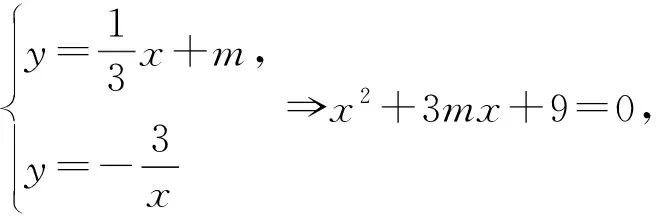
评注：先构建模型，把动点设置在反比例函数图像上，然后从解析几何角度，求出与已知直线平行的切线，再利用两平行直线之间的距离公式，得出函数的最小值，思路妥帖自然.

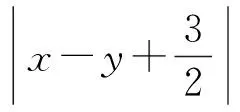
评注：化归为点到直线的距离公式的模型，模仿上一题的思维模式，求出与已知直线平行的切线方程，再运用两两平行直线之间的距离公式求出最小值.

点到直线的距离公式，无论是公式推导方法，还是公式的用途，都是解析几何里浓墨重彩的绚丽华章.对点到直线的距离公式的研发和挖掘，是一件非常具有价值的工作，而构造点到直线的距离公式的模型，求解最值问题，应成为数学解题的理想与追求.

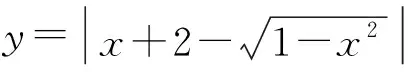
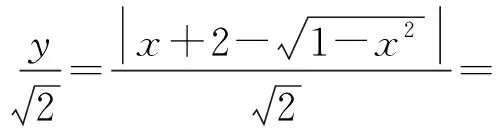
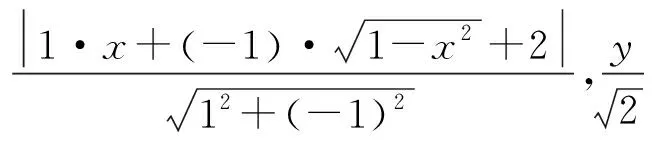
图4

评注：本题重点在于对函数解析式的重组和变形，从而构造出点到直线的距离公式的模型.由于动点在半圆周上运动，就可利用几何方法破解.

例8 已知a,b∈R，关于x的方程x4+ax3+2x2+bx+1=0有一个实根，求a2+b2的最小值.

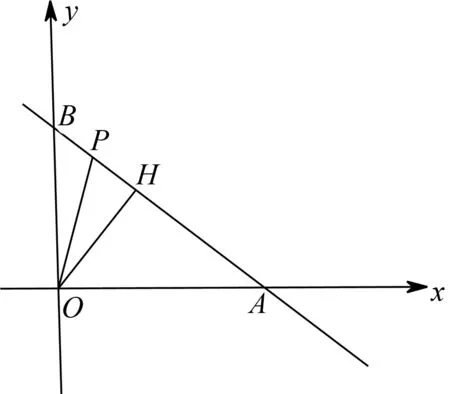
图5

评注：本题关键在于变换思维视角，将方程视作一条直线.再从几何角度，成功转化为点到直线的距离公式模型，接着恒等变形，进一步化归为基本不等式求出最小值.

由此可见，三个距离公式既是计算距离针对性很强的工具，又是我们因数构形的一种思维模型，只要我们开动脑筋，合理猜想，精心构造，就可收获成功的喜悦.