封隔器仿生六棱柱齿状卡瓦微牙痕及稳定性

徐建宁， 邓冲， 李万钟

(西安石油大学机械工程学院， 西安 710065)

封隔器是在油水井井筒中密封井内工作管柱与井筒内环形空间的封隔工具，对不同油层和水层进行封隔，并能够承受一定压力差[1]。卡瓦式封隔器被广泛应用于完井、压裂、酸化、注水、试油等各个石油开采技术领域中[2]，卡瓦作为封隔器核心元件之一，在封隔器锚定时起到支撑封隔器、锁定胶筒的作用[3]，是保证封隔器工作可靠性的重要组成部分。

通常油井套管的壁厚较薄，在一些固井质量较差或未注水泥浆的井段内，由于封隔器卡瓦对套管的挤压作用，卡瓦牙有可能在与套管接触面形成咬痕，过大的嵌入深度有可能会导致套管损坏、失效，使套管壁遭到破坏，且在油井二次作业中，如果套管壁表面被卡瓦严重损伤，被咬伤的井段将无法再进行二次封隔[4]，甚至无法解封或者致使套管被挤裂、腐蚀。封隔器卡瓦咬入套管的深度是评价封隔器定位性能和衡量套管损伤程度的重要指标[5]。因此，在保证封隔器正常工作的情况下，降低卡瓦对套管壁的损伤程度，即减轻卡瓦在套管内表面产生的牙痕，就要不断对卡瓦进行优化设计，使卡瓦咬合套管的作用力合理分布[6]。

经过35亿年的进化，自然界生物体表形成了许多结构奇妙、性能优异、功能丰富的表面织构，为摩擦学研究者提供了极佳的表面仿生设计素材。蝾螈足垫六边形凸起结构有助于进一步提高面积率，该凸起结构具有增摩效果，且摩擦力随其面积率的增加而迅速攀升[7]。树蛙脚掌由多边形棱柱形状的表皮细胞密排而成，其中以六棱柱形为主，仿树蛙的六棱柱表面不仅能够有效地消除黏-滑现象，且能够产生远高于干摩擦的稳定持久的边界摩擦力[8]。本文中所要研究的封隔器卡瓦牙齿模仿蝾螈足垫和树蛙脚掌的密排六棱柱形状，建立仿生六棱柱齿状卡瓦模型，运用有限元数值模拟的方法对其结构参数进行优化，并与常规齿状卡瓦进行对比，探究其应力和变形规律，以期得到可在套管内表面产生微牙痕效果的仿生六棱柱齿状卡瓦。

1 卡瓦有限元三维模型的建立

卡瓦咬合套管的行为属于带尖齿的非线性弹塑性接触问题，从理论上直接研究非常困难。且在接触过程中会形成复杂的应力以及发生塑性变形，也可能发生穿透使结果很难收敛[9]。但是随着非线性有限元软件分析计算能力的增强，计算机计算速度的提高，用大型非线性有限元分析软件对卡瓦锚定系统进行研究已经成为可能和一种必然趋势[10]。

1.1 模型建立与材料选择

1.1.1 常规齿状和仿生六棱柱齿状卡瓦牙型结构参数对比

常规齿状卡瓦的牙型结构参数如图1所示，其中α为卡瓦牙倾角，β为卡瓦牙顶角，b为卡瓦牙宽，γ为卡瓦锥角。

仿生六棱柱齿状卡瓦的牙型结构参数如图2所示，卡瓦牙呈带有斜面的正六棱柱形，其中α′为卡瓦牙倾角，b′为卡瓦牙宽，即卡瓦牙沿齿高方向投影正六边形外接圆直径d=b′，s为六棱柱卡瓦牙间距，γ′为卡瓦锥角，c为卡瓦牙上底高。相比于常规齿状卡瓦，仿生六棱柱齿状卡瓦增加了卡瓦牙沿齿高方向投影正六边形外接圆直径d、相邻六棱柱卡瓦牙间距s两个主要牙型参数和卡瓦牙上底高c一个次要牙型参数。

1.1.2 常规齿状和仿生六棱柱齿状卡瓦三维模型

建立常规齿状封隔器卡瓦模型和仿生六棱柱齿状卡瓦模型，如图3所示。

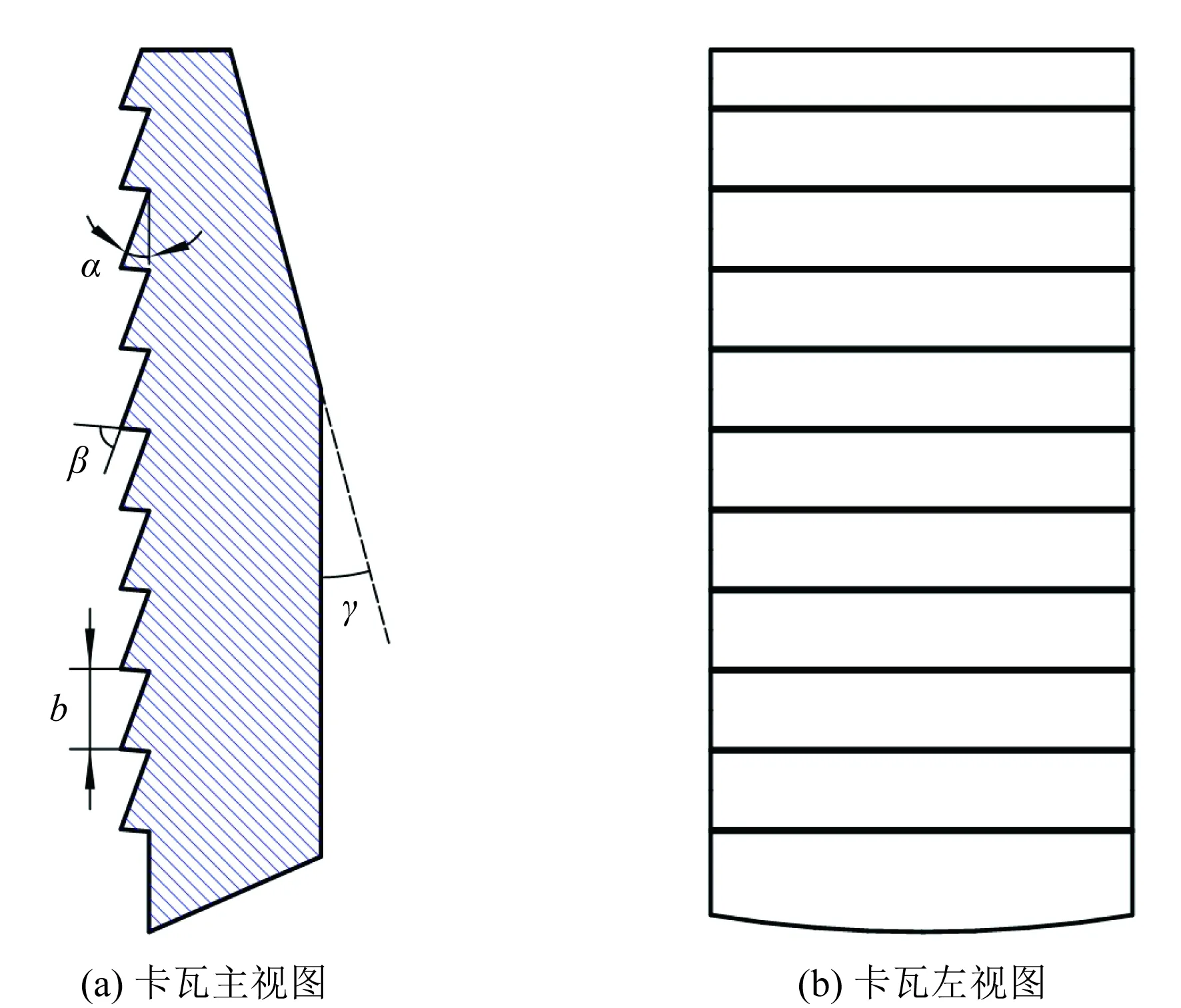
图1 常规齿状卡瓦牙型结构参数Fig.1 Structural parameters of conventional tooth slip

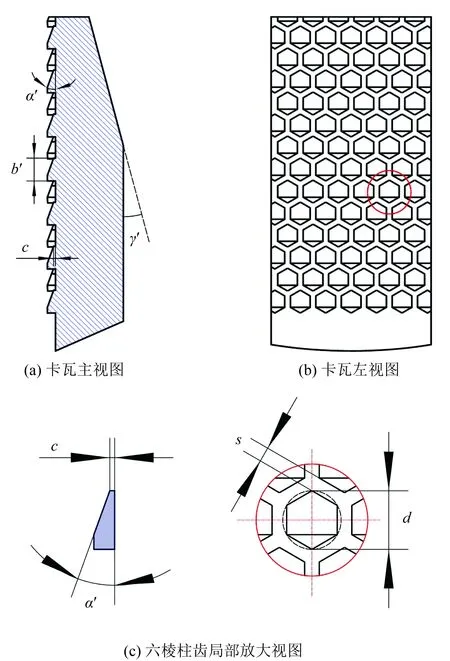
图2 仿生六棱柱齿状卡瓦牙型结构参数Fig.2 Structural parameters of hexagonal prism tooth slip

为了便于对封隔器卡瓦咬合套管的动作进行有限元模拟，对模型进行了进一步的简化，即把锥体、卡瓦和套管当作一个整体系统来分析处理，如图4所示。为减少计算量，针对单瓣卡瓦并截取一定圆弧宽度和长度的椎体、套管进行分析，其中截取套管圆弧宽度大于卡瓦的圆弧宽度，以免产生边界效应，造成计算误差。建立刚性斜面体来限制卡瓦的径向和轴向位移。封隔器坐封时，在外加载荷作用下锥体推动卡瓦沿径向移动，当达到预定坐封载荷时，卡瓦牙咬入套管内壁，坐封完成[1]。锥体、卡瓦和套管的材料参数如表1所示，其中卡瓦的力学性能要优于套管的力学性能[11]。

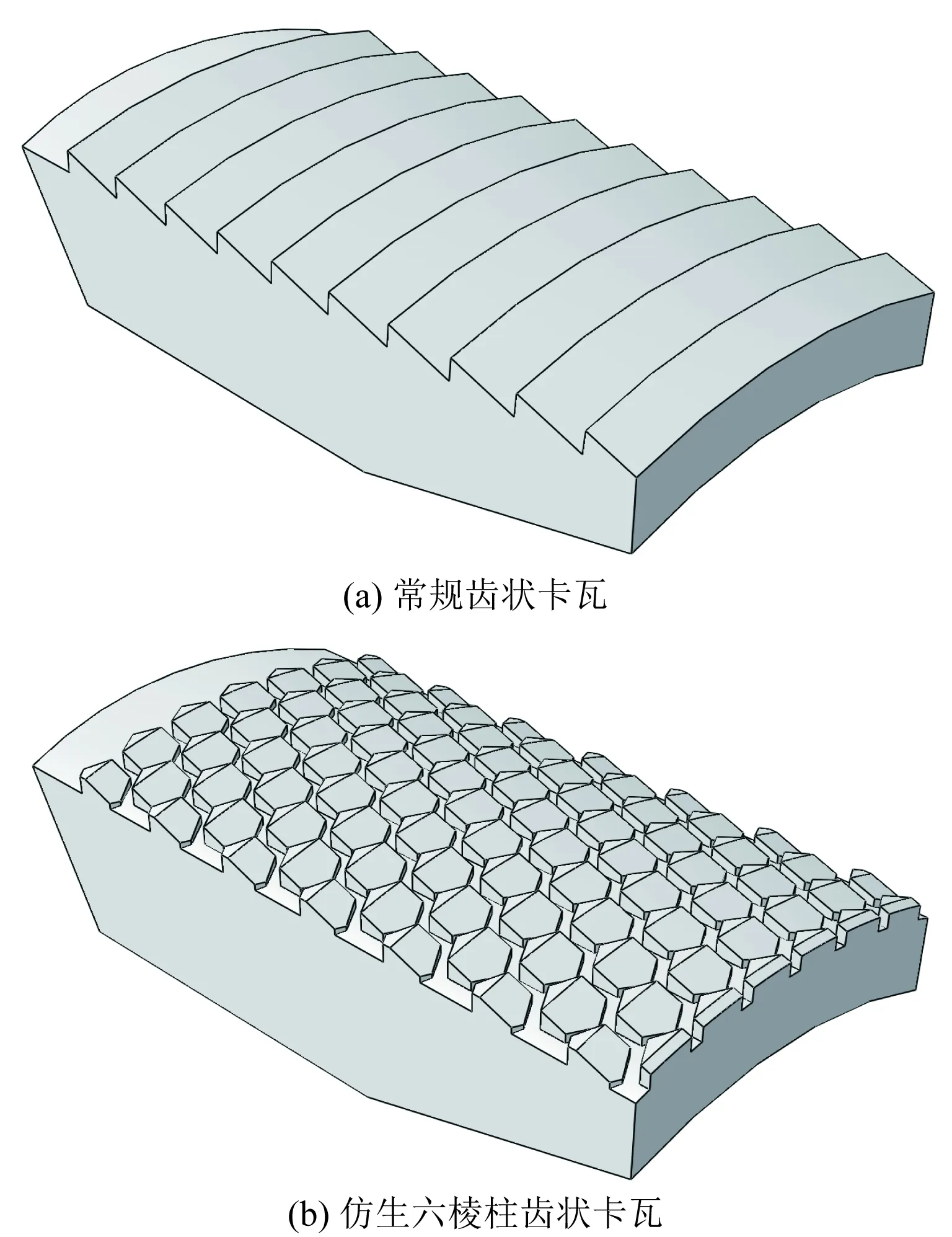
图3 卡瓦三维有限元模型Fig.3 Three-dimensional finite element model of slip

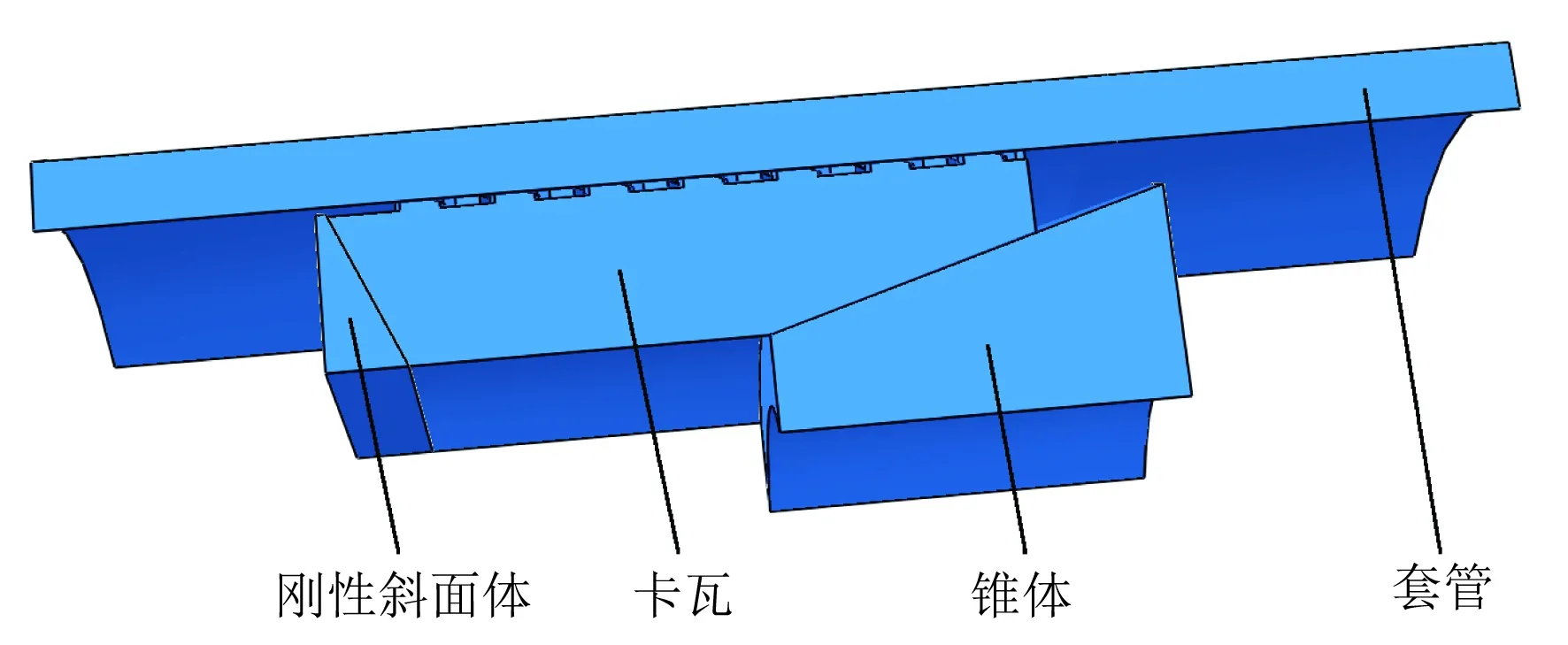
图4 锥体-卡瓦-套管三维接触有限元模型Fig.4 Three-dimensional contact finite element model of cone, slip and casing

1.2 网格划分与边界条件设置

如图5所示，两种齿状卡瓦都采用C3D4(四节点线性四面体)单元，并且对与套管接触的卡瓦齿部分进行网格细化。对卡瓦从疏到密划分三种不同的网格密度，划分的常规齿状卡瓦的单元总数分别为97 790、116 066、130 303，节点总数分别为19 379、22 914、25 566；划分的仿生六棱柱齿状卡瓦的单元总数分别为206 807、249 147、286 267，节点总数分别为41 021、49 357、56 252。

锥体-卡瓦-套管三维接触有限元模型的网格划分如图6所示。其中套管模型采用扫掠网格划分技术，选择C3D8R(八节点六面体线性减缩积分)单元，对套管与卡瓦接触部分的网格进一步加密，提高计算精度，最终划分的套管单元总数为26 964，节点总数为32 508；锥体模型采用结构化网格划分技术，同样选择C3D8R单元，最终划分的锥体单元总数为5 750，节点总数为6 864；斜面体模型设置为刚体，在进行网格划分时采用Quad(四边形)单元，最终划分的斜面体单元总数为2 394，节点总数为2 396。

图5 卡瓦网格划分Fig.5 Slip meshing

表1 锥体、卡瓦和套管的材料参数Table 1 Material parameters of cone, slip and casing

边界条件的设置如图7所示。在套管外壁施加完全固定约束，在锥体上施加沿轴向的位移，在楔形面的作用下使卡瓦咬紧套管。

图6 锥体-卡瓦-套管三维接触网格划分Fig.6 Three-dimensional contact meshing of cone, slip and casing

图7 锥体-卡瓦-套管接触有限元模型边界条件设置Fig.7 Boundary condition setting of cone, slip and casing contact finite element model

卡瓦咬入套管过程属于接触非线性问题，套管发生局部塑形变形属于材料非线性问题，故该变形过程属于结构非线性问题[12]。锥体-卡瓦-套管三维接触模型主要涉及卡瓦与套管、卡瓦与锥体和卡瓦与刚性斜面体的接触，其接触类型均采用面对面接触和有限滑移公式，法向接触属性为“硬接触”，切向接触摩擦模型为“库仑摩擦”。

2 结构参数优化和仿真结果分析

2.1 仿生六棱柱齿状卡瓦牙型结构参数的优化

通过分析卡瓦牙齿在套管内表面产生牙痕的深度及其分布规律，设计合理的仿生卡瓦，得到可产生微牙痕效果的仿生六棱柱齿状卡瓦牙型结构参数。以卡瓦牙在套管内表面产生的应力和牙痕深度作为目标函数，把卡瓦牙上底高c=0.5 mm和卡瓦锥角γ′=15°作为固定结构参数，利用有限元分析软件分别对六棱柱齿状的卡瓦牙倾角α′、卡瓦牙沿齿高方向投影正六边形外接圆直径d和相邻六棱柱卡瓦牙间距s三个牙型结构参数进行了数值模拟优化，确定出最佳结构参数组合。

2.1.1 卡瓦牙倾角α′变化时目标函数的变化规律

对锥体-卡瓦-套管系统开展接触非线性有限元计算，当γ′=15°、c=0.5 mm、d=6 mm、s=1 mm时，分别取卡瓦牙倾角α′=16°、18°、20°、22°，比较套管的Von Mises应力值、牙痕深度U和卡瓦与套管的接触面积S，数值模拟结果如表2所示。

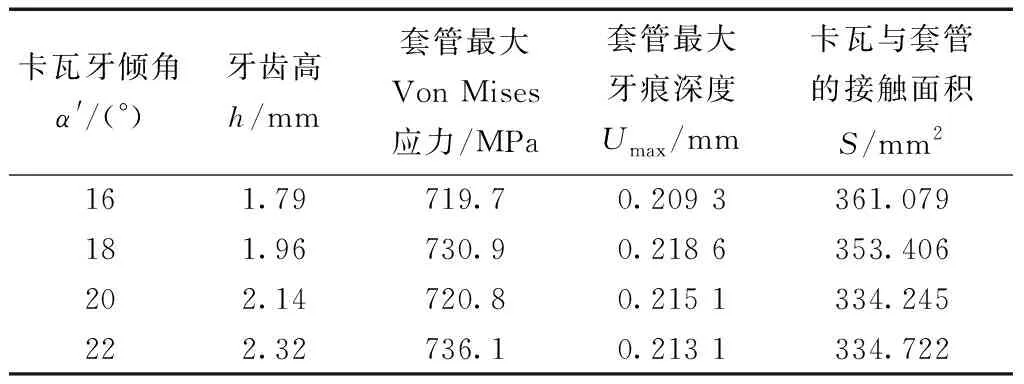
表2 卡瓦牙倾角α′变化时目标函数的变化规律Table 2 Variation law of objective function when slip tooth inclination changes

从表2整体上可以看出，卡瓦牙倾角的变化对套管的Von Mises应力和牙痕深度影响较小。同时，随着卡瓦牙倾角的逐渐增大，卡瓦与套管的接触面积S逐渐减小。综合分析，取α′=18°、20°和22°作为优化卡瓦牙倾角。

2.1.2 卡瓦牙沿齿高方向投影正六边形外接圆直径d变化时目标函数的变化规律

当γ′=15°、c=0.5 mm、α′=20°、s=1 mm时，分别取d=6、8、10、12 mm，比较套管的Von Mises应力、牙痕深度U和卡瓦与套管的接触面积S，数值模拟结果如表3所示。

表3 卡瓦牙沿齿高方向投影正六边形外接圆直径d变化时目标函数的变化规律Table 3 The variation law of objective function when the diameter of hexagonal circumcircle projected by slip tooth along the direction of tooth height changes

从表3可以看出，正六边形外接圆直径d=6 mm时，套管的Von Mises应力和牙痕深度都最小，即卡瓦在套管上产生的牙痕深度最浅。同时，随着正六边形外接圆直径的逐渐增大，卡瓦与套管的接触面积S逐渐增大。综合分析，取d=6 mm作为优化卡瓦牙沿齿高方向投影正六边形外接圆直径。

2.1.3 相邻六棱柱卡瓦牙间距s变化时目标函数的变化规律

当γ′=15°、c=0.5 mm、α′=20°、d=6 mm时，分别取s=0.5、1、1.5、2 mm，比较套管的Von Mises应力、牙痕深度U和卡瓦与套管的接触面积S，数值模拟结果如表4所示。

从表4可以看出，当相邻六棱柱卡瓦牙间距s=0.5 mm时，套管的Von Mises应力和牙痕深度都最小，即卡瓦在套管上产生的牙痕深度最浅。同时，随着相邻六棱柱卡瓦牙间距的逐渐增大，卡瓦与套管的接触面积S逐渐减小。综合分析，取s=0.5 mm作为优化相邻六棱柱卡瓦牙间距。

对上述所选出的卡瓦牙倾角、正六边形外接圆直径和相邻六棱柱卡瓦牙间距的优化参数进行组合，如表5所示。

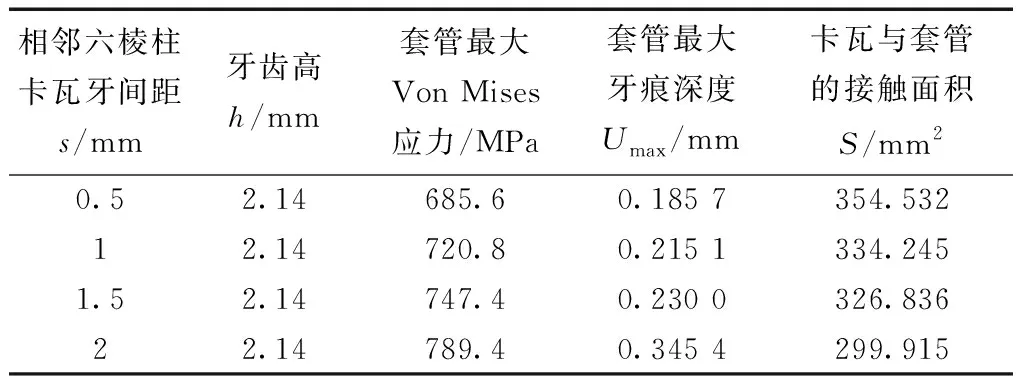
表4 相邻六棱柱卡瓦牙间距s变化时目标函数的变化规律Table 4 Variation law of objective function when the distance between adjacent hexagonal prism slip teeth changes

对以上三组结构参数分别再进行数值模拟，则从1～3组合顺序号下的各优化参数对套管最大Von Mises应力和最大牙痕深度影响的变化曲线如图8所示。

从图8可以明显得出，组合顺序号1各参数下的套管最大Von Mises应力值和套管最大牙痕深度值最小，即在c=0.5 mm和γ′=15°为固定结构参数下，α′=18°、d=6 mm和s=0.5 mm和是仿生六棱柱齿状卡瓦最佳牙型结构参数组合。

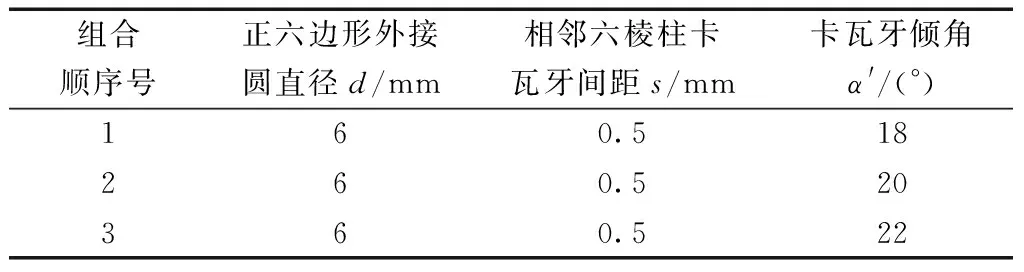
表5 结构参数组合Table 5 Structural parameter combination

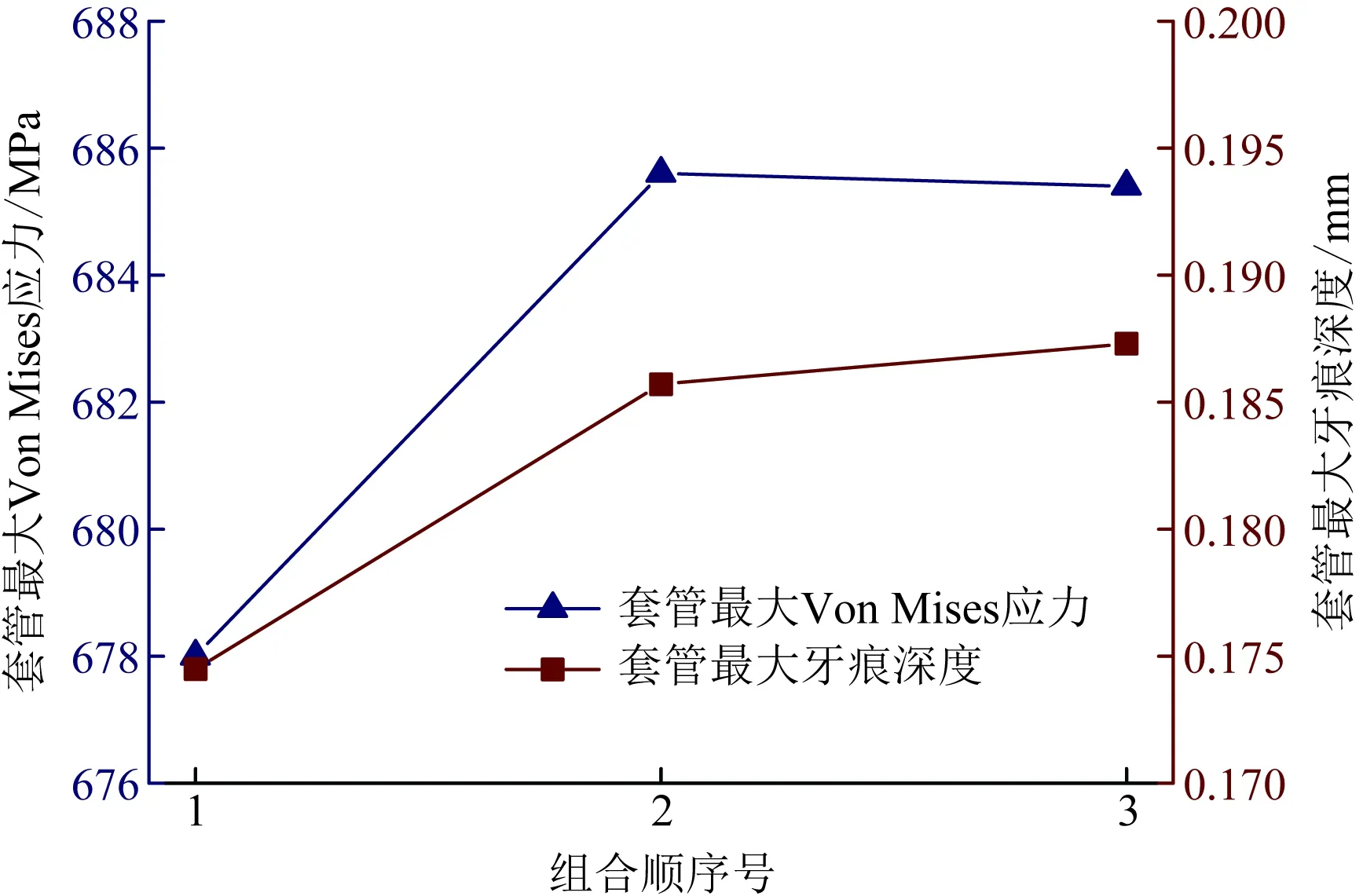
图8 不同组合号下套管最大Von Mises应力和最大牙痕深度变化曲线Fig.8 Variation curves of maximum Von Mises stress and maximum embeding depth of casing under different combination numbers

2.2 常规齿状和仿生六棱柱齿状卡瓦有限元仿真结果对比分析

目前采用正交实验法已对常规齿状卡瓦结构参数进行了优化改进，得出常规齿状卡瓦最优结构参数组合为：α=20°、β=75°、b=8 mm、γ=15°[13]。由2.1节优化出的仿生六棱柱齿状卡瓦最佳结构参数组合为：α′=18°、d=6 mm、s=0.5 mm、γ′=15°和c=0.5 mm。对优化后的两种卡瓦开展有限元数值模拟仿真，得到卡瓦的Von Mises应力云图如图9所示，套管的Von Mises应力云图和牙痕深度U云图如图10、图11所示。

从图9可以看出，两种齿状卡瓦与锥体接触端的齿所承受的应力极大，且卡瓦与锥体接触的楔形面两端应力非常集中，最大Von Mises应力达到835 MPa，远超过卡瓦材料的屈服极限。同时，越靠近卡瓦底端的齿所承受的应力逐渐减小。

如图10和图11所示，两种齿状卡瓦在套管内表面上产生的应力和变形同样遵循从上至下依次减小的规律。经对比发现，优化结构参数后的仿生六棱柱齿状卡瓦在套管上产生的最大Von Mises应力小于优化后的常规齿状卡瓦在套管上产生的最大Von Mises应力；经优化结构参数的仿生六棱柱齿状卡瓦咬合套管后在套管内表面产生的最大牙痕深度小于优化后的常规齿状卡瓦在套管内表面产生的最大牙痕深度。通过对优化结构参数后的常规齿状卡瓦和仿生六棱柱齿状卡瓦分别划分三种不同的网格密度并进行三组数值模拟，由表6和表7可以得出结论，优化结构参数之后的仿生六棱柱齿状卡瓦比经优化后的常规齿状卡瓦在套管内表面产生的应力和牙痕深度要小，且应力减小了14.61%～15.25%，牙痕深度减小了44.12%～47.10%，证明了仿生六棱柱齿状卡瓦的微牙痕效果。

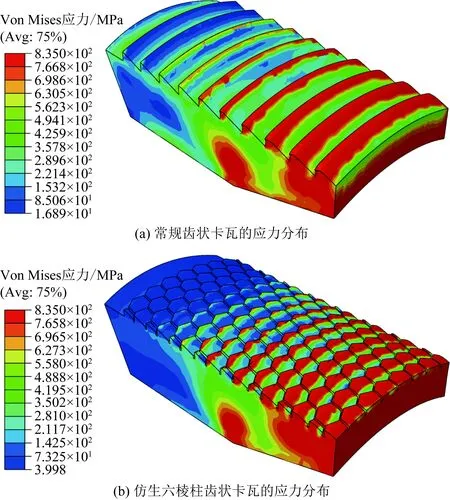
图9 不同卡瓦的Von Mises应力云图Fig.9 Von Mises stress distribution of different slips

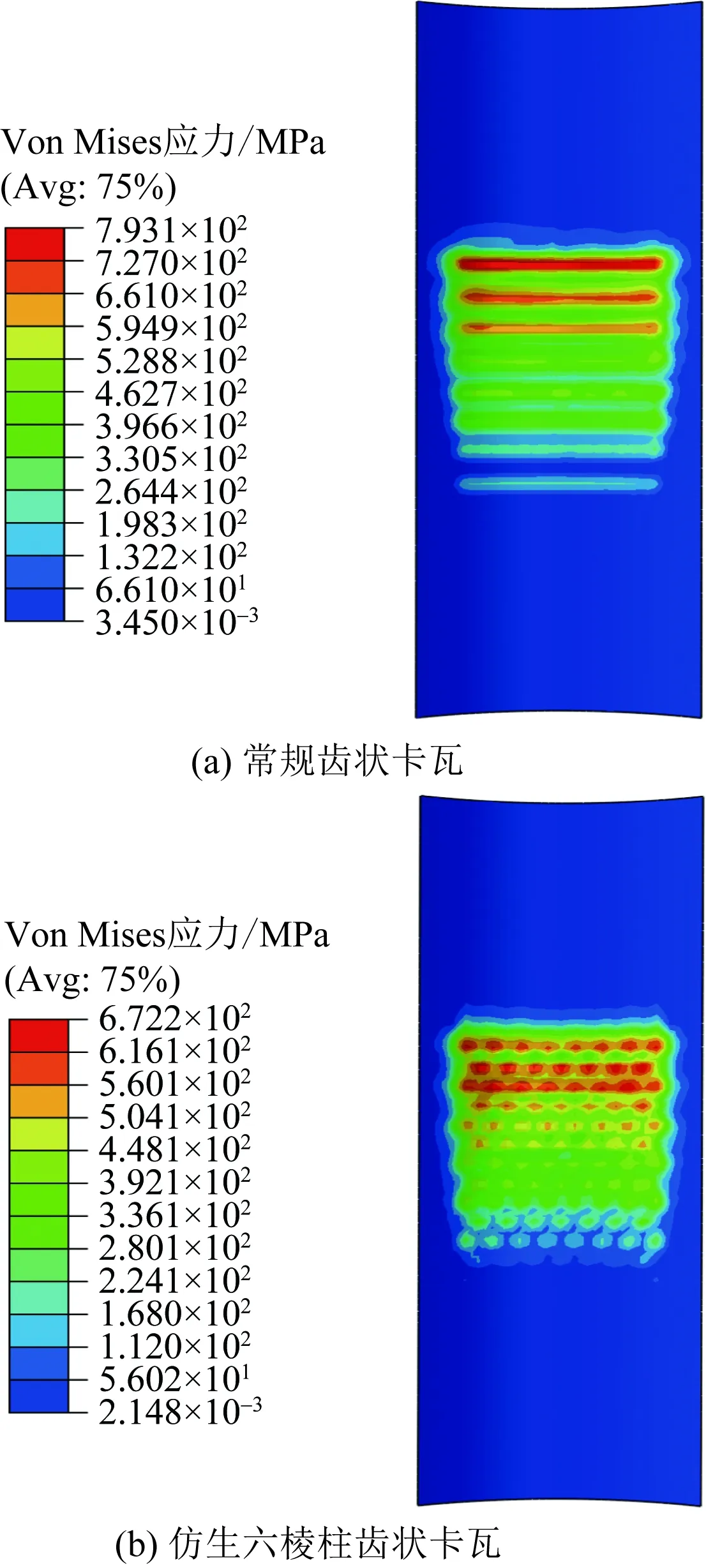
图10 不同卡瓦咬合套管的Von Mises应力云图Fig.10 Von Mises stress distribution on casing with different slips

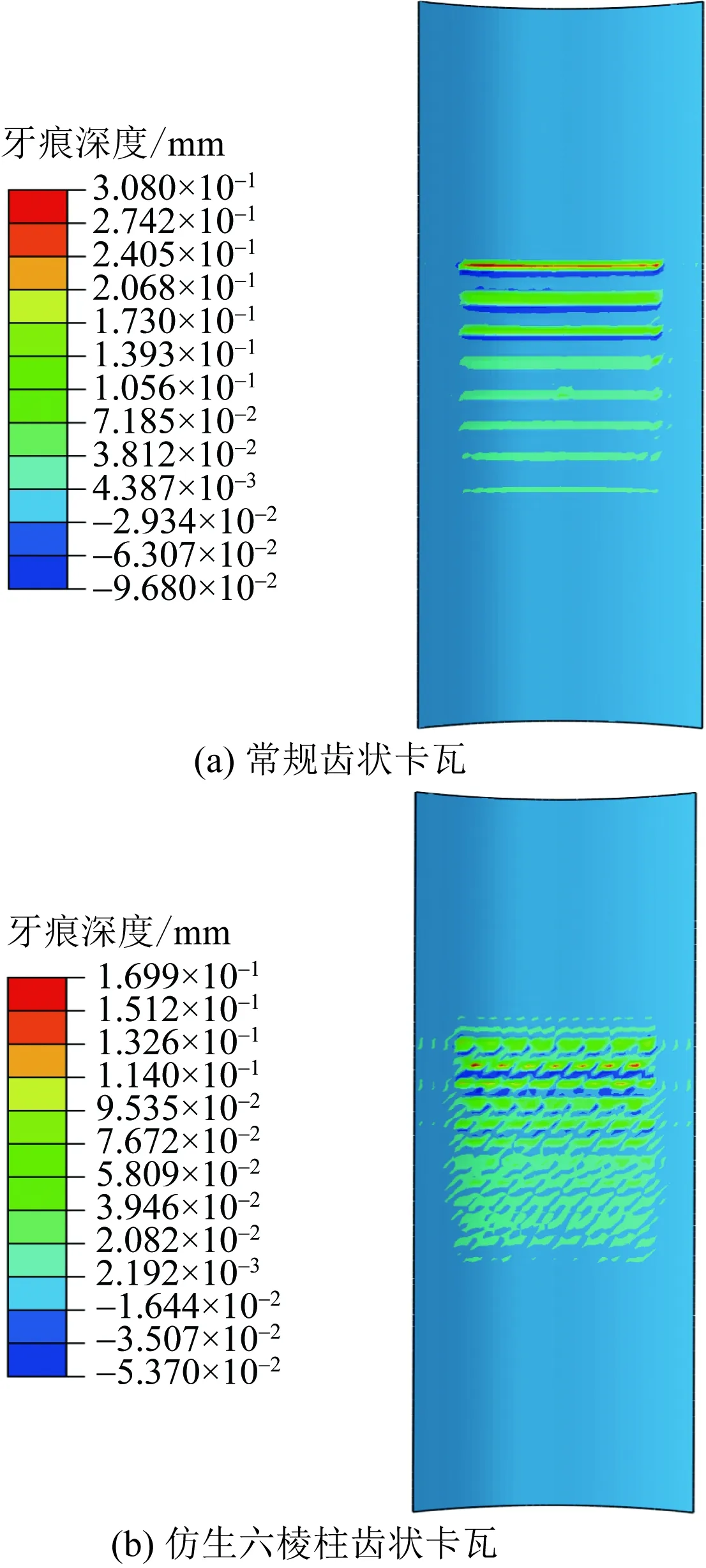
图11 不同卡瓦咬合套管牙痕深度云图Fig.11 Radial displacement distribution on casing with different slips

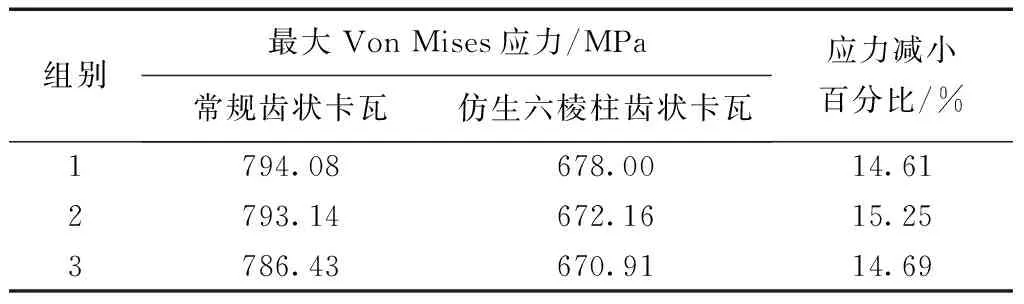
表6 不同卡瓦优化后多次模拟的应力结果对比Table 6 Stress comparison of multiple simulations of optimized different slips

表7 不同卡瓦优化后多次模拟的牙痕深度结果对比Table 7 Embeding depth comparison of multiple simulations of optimized different slips

3 摩擦系数对卡瓦与套管非线性接触的影响

本研究重在探究卡瓦与套管的接触，因此对卡瓦与锥体和卡瓦与刚性斜面体的接触不做过多研究。分别取卡瓦与套管接触面的摩擦系数f为0.1、0.15、0.2、0.25、0.3、0.35、0.4，通过有限元数值模拟探究摩擦系数的改变对卡瓦在套管产生的应力、应变的影响[14]，以及对卡瓦与套管接触压力的合力(normal contact force,CFN)、摩擦应力的合力(contact frictional stress,CFS)和接触面积(contact area, CAREA)的影响。

改变优化结构参数后的常规齿状和仿生六棱柱齿状卡瓦与套管接触面的摩擦系数，其在套管上产生的最大Von Mises应力和最大牙痕深度Umax的变化曲线如图12所示。

从图12可以看出，对于常规齿状卡瓦，摩擦系数的改变对套管的最大Von Mises应力和牙痕深度的影响较大，随着卡瓦与套管接触面摩擦系数的增大，套管的最大Von Mises应力和牙痕深度也逐渐增大。而对于仿生六棱柱齿状卡瓦，摩擦系数的改变对套管的最大Von Mises应力和牙痕深度的影响甚微，这说明了仿生六棱柱齿状卡瓦比常规齿状卡瓦的具有更好的稳定性。

图12 不同摩擦系数对卡瓦与套管接触的应力和牙痕深度影响Fig.12 Influence of different friction coefficients on stress and embeding depth of slip in contact with casing

改变优化结构参数后的常规齿状和仿生六棱柱齿状卡瓦与套管接触面的摩擦系数，得到不同摩擦系数下卡瓦与套管接触压力的合力(CFN)、摩擦应力的合力(CFS)和接触面积S(CAREA)与接触时间的关系曲线，如图13～图15所示。

如图13、图14所示，随着接触时间的增大，常规齿状卡瓦与套管接触压力的合力、摩擦应力的合力都以近似呈抛物线的形式增大；仿生六棱柱齿状卡瓦与套管接触压力的合力起初呈线性增大，之后很快就处于平稳状态，摩擦应力的合力也呈相同的趋势。在卡瓦牙齿与套管接触时，从图15可分析出常规齿状卡瓦与套管的接触面积起初以近指数形式迅速增大，在一段平稳过渡之后，接触面积又以不同的曲线形式增大，表现出明显的不稳定性；仿生六棱柱齿状卡瓦与套管的接触面积先以近似线性增大，简短的平滑过渡之后再增大，最终有达到平稳状态的趋势。

摩擦系数的增大对卡瓦与套管接触压力的合力和接触面积有一定的影响，且影响呈下降的趋势。显然，随着摩擦系数增大，摩擦应力的合力也随之增大，数值模拟的结果也很好的验证了库仑摩擦公式中法相接触力与摩擦力的关系。综上所述，进一步说明了仿生六棱柱齿状卡瓦比常规齿状卡瓦的稳定性更好。

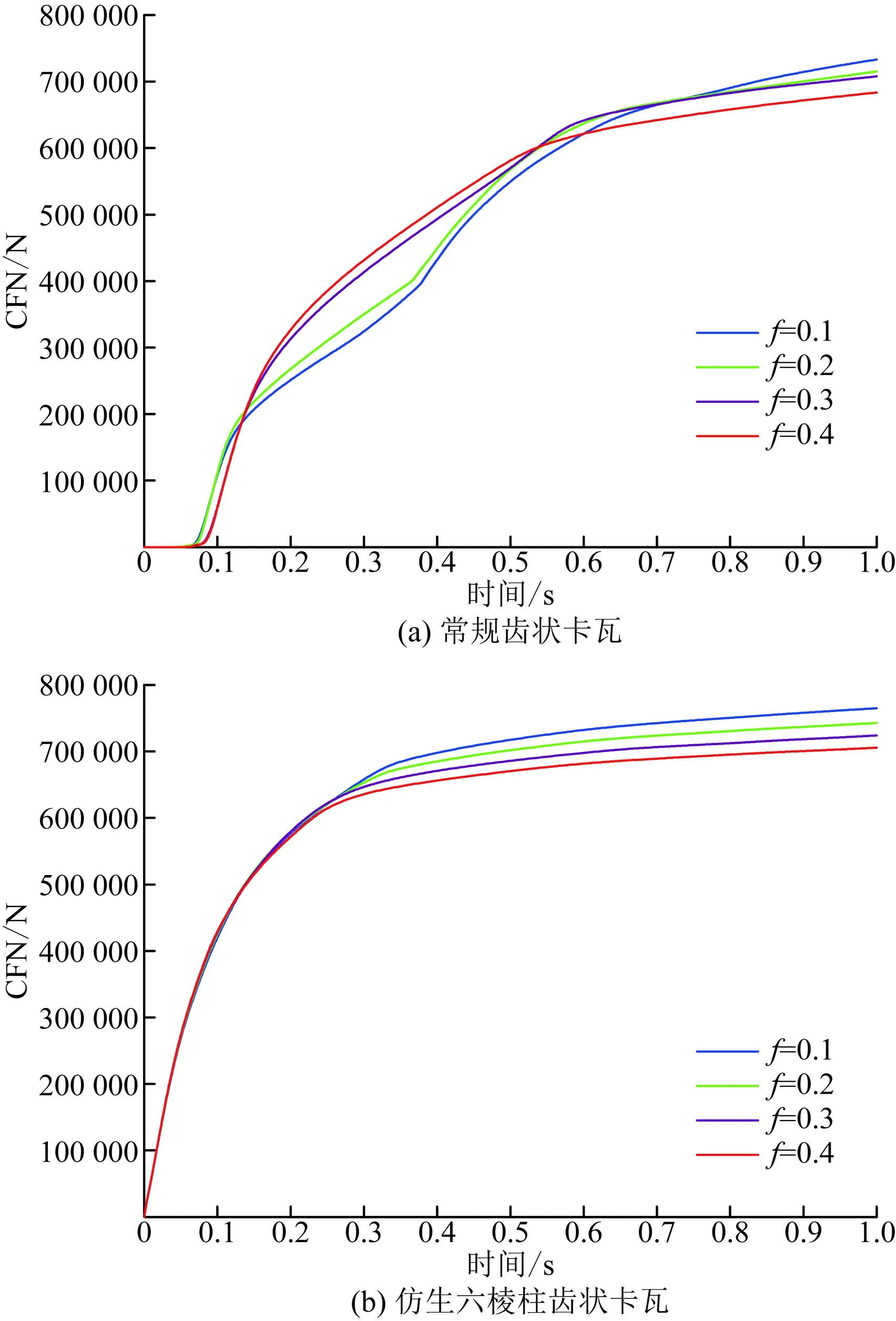
图13 不同摩擦系数下卡瓦与套管接触压力的合力Fig.13 Normal contact force between slip and casing under different friction coefficients

图14 不同摩擦系数下卡瓦与套管摩擦应力的合力Fig.14 Contact frictional stress between slip and casing under different friction coefficients

图15 不同摩擦系数下卡瓦与套管的接触面积Fig.15 Contact area between slip and casing under different friction coefficients

4 结论

(1)本文中所研究的卡瓦模型适用于5.5英寸(139.7 mm)套管，套管壁厚为7.72 mm。通过对比常规齿状卡瓦的牙型结构参数，构建仿生六棱柱齿状卡瓦的牙型结构参数，建立锥体-卡瓦-套管三维接触有限元模型，并利用有限元数值模拟对仿生六棱柱齿状卡瓦的牙型结构参数进行正交优化，得出仿生六棱柱齿状卡瓦的牙型最佳结构参数为：α′=18°、d=6 mm、s=0.5 mm、γ′=15°和c=0.5 mm。

(2)对比结构参数优化之后的仿生六棱柱齿状卡瓦和常规齿状卡瓦在套管内表面产生的应力和牙痕深度。优化后的仿生六棱柱齿状卡瓦比优化后的常规齿状卡瓦在套管内表面产生的应力和牙痕深度要小，且应力减小了14.61%～15.25%，牙痕深度了减小44.12%～47.10%，证明了仿生六棱柱齿状卡瓦的微牙痕效果。

(3)通过改变卡瓦与套管接触面的摩擦系数，由数值模拟得出，对于与常规齿状卡瓦，摩擦系数的改变对套管的应力和变形的影响较大，而对于仿生六棱柱齿状卡瓦，摩擦系数的改变对套管的应力和变形的影响甚微。对比常规齿状卡瓦和仿生六棱柱齿状卡瓦分别咬合套管时，仿生六棱柱齿状卡瓦与套管接触压力的合力、摩擦应力的合力和接触面积与接触时间的关系曲线明显比常规齿状卡瓦的要更平滑且较快的处于稳定状态。这些都表明了仿生六棱柱齿状卡瓦稳定性优于常规齿状卡瓦。