基于有限元法的正交直齿面齿轮分扭传动系统啮合刚度计算

张 涛 朱 楚 熊剑锋

（中国航发湖南动力机械研究所，湖南 株洲 412002）

面齿轮传动（Face Gear Drive）是一种面齿轮和圆柱齿轮相啮合的传动结构，相比于锥齿轮传动，由于面齿轮传动不受轴向力作用，其轴承支撑系统可以设计得比较简单，系统结构重量上有明显优势，已在新一代阿帕奇直升机传动系统中成功应用。

Litvin F.L[1-5]等人基于切削蜗杆的生成方法建立了与渐开线小直齿轮啮合的面齿轮传动形式，提出了一种分析方法，确定了切削蜗杆的参数和修整方法，并开发了小齿轮和面齿轮啮合接触应力计算程序，对面齿轮传动副进行了接触分析。

唐进元在面齿轮传动的基本理论、啮合特性、接触特性、强度、误差检测、动力学以及粗精加工等方面开展了较为全面的研究[6-9]。

1 正交直齿面齿轮分扭传动系统有限元建模

本文的面齿轮分扭传动系统结构为上、下两个面齿轮分别与中间的五个直齿轮同时啮合，上、下两个面齿轮同轴布置，中间五个直齿轮与面齿轮轴线垂直，左、右输入齿轮和左、右惰轮以面齿轮轴线与尾传惰轮轴线组成的中间平面为基准对称布置，其结构如图1 所示。面齿轮分扭传动系统各轮齿参数如表1 所示。

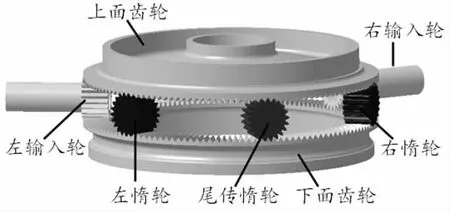
图1 面齿轮分扭传动系统结构

表1 面齿轮分扭传动系统齿轮参数

一般地，有限元建模分为模型导入、装配、网格划分、定义材料属性、定义载荷与边界条件、提交计算与提取结果等几个步骤。将面齿轮分扭传动系统中的圆柱齿轮和面齿轮导入Hypermesh 中进行网格划分，并将划分好的面齿轮分扭传动系统网格模型导入ABAQUS 中，进行以下前处理操作。

1.1 设置材料参数

齿轮采用9310 钢材料，弹性模量为200GPa，泊松比为0.316。

1.2 定义接触对

建立接触对按以下原则：

1.2.1 一对齿轮副中常有几个轮齿同时接触的情况，一定从旋转方向最后一个接触的轮齿开始，建立接触对。

1.2.2 尽量控制接触的两个轮齿网格密度一致。

1.2.3 在不能判断接触对上哪个面为受力面时，把轮齿的正面和背面都选中为一个曲面，仿真过程自动输出作用力，并可根据应力云图判断实际的受力情况。

1.3 设置分析步

按四个步骤进行仿真：第一步建立接触；第二步从动轮释放约束，并施加一个小载荷；第三步施加实际载荷；第四步施加转角。

1.4 边界条件

采用静态隐式计算方法，模拟系统在静态（无转速）的受力情况（不考虑各轮齿重力）。系统有限元仿真模型中，根据实际工况（输入转速和额定负载等）设边界条件如图2，上、下面齿轮采用全局坐标系，五个直齿轮采用各自旋转中心为原点建立的局部坐标系；负载扭矩分别加载到尾传齿轮和上面齿轮。载荷工况为：上面齿轮负载扭矩21000N·m，尾传负载扭矩1000N·m。本文所述计算方法不考虑输入到输出的效率损失。建立好的面齿轮分扭传动系统有限元分析模型如图3 所示。

图2 坐标系与边界条件

图3 面齿轮分扭传动系统有限元整体模型

2 面齿轮副齿轮啮合刚度计算方法

在上述有限元计算结果中可直接提取全局坐标系下，各齿轮副的接触力和接触点坐标以及各轮齿啮合过程中的实际转角等参数。这些参数是刚度解析计算中的中间变量。在直齿轮刚度计算中，力臂往往看成恒定值，用基圆半径代替。然而，本面齿轮分扭传动系统多用于重载工况，轮齿模数相对较大，相应的轮体尺寸较大。因此，在计算啮合刚度过程中，为减少理论误差，有必要计算精确的时变力臂。

如图4 所示，单齿啮合周期内，假设面齿轮齿面啮合轨迹上一系列点的坐标为Pi（xi，yi，zi），Pi点受到的接触力为Fi，且该接触力的各轴分力分别是fx，fy，fz。面齿轮轴线为L。Qi是接触力Fi所在的延长线上另一点。点Qi和Si为轴线L 和接触力Fi延长线的公垂线上两点。面齿轮约束在它轴线上的M 点。

图4 齿轮副接触时变力臂

根据空间几何原理，全局坐标系[O；x，y，z]中，轴线L的方向向量为

接触点Pi 的接触力所在的延长线方向向量为

轴线和受力线的公垂向量可用这两个向量的矢积表示为

又因为O 是轴线上一点，Pi是受力延长线上一点，这两点可构建向量

公式（4）向量在公式（3）公垂向量方向上的投影即为空间垂直距离，该垂直距离即为精确的力臂，即

带入各向量坐标值，时变力臂的计算公式可简化为：

根据时变力臂和传递误差即可计算轮齿所对应的变形量：

在实际工况下，对于同轴面齿轮分扭传动系统中的任何一个齿轮副，都有可能有多个轮齿同时进行啮合，从而会出现单齿啮合和多齿啮合的交替情况。研究单齿啮合区的动力关系时，轮齿对可简化为弹簧系统。故单齿对的啮合刚度可计算为

多齿啮合区时，齿轮副等效于多个弹簧系统同时发生作用，假设同时啮合的单齿对数为i。根据变形关系，多个轮齿同时接触时，齿轮副整体变形时所消耗的能量是各个接触的单齿变形时消耗的能量的总和。所以，多齿啮合的综合啮合刚度，等效于多个弹簧的并联刚度，即齿轮副的啮合刚度为

3 正交直齿面齿轮分扭传动系统啮合刚度计算

根据本文建立的面齿轮分扭传动系统有限元分析模型和啮合刚度计算方法，采用表2 中的工况参数，计算得到了图5 中面齿轮分扭传动系统结构各齿轮啮合副的时变啮合刚度，如图5 所示。

表2 工况参数

由图5 可知在同轴直齿面齿轮分扭传动系统中，所有齿轮副的啮合刚度是有差异的，本质原因是不同的齿轮副受力大小不一致。总体来说，惰轮构成的齿轮副的啮合刚度最小，这是因为惰轮本身受力较小。由于结构的对称性（相对于尾传轴线），当与同一个面齿轮构成齿轮副时，左、右输入轮的啮合刚度基本是一致的，左、右惰轮的啮合刚度也基本是一致的。

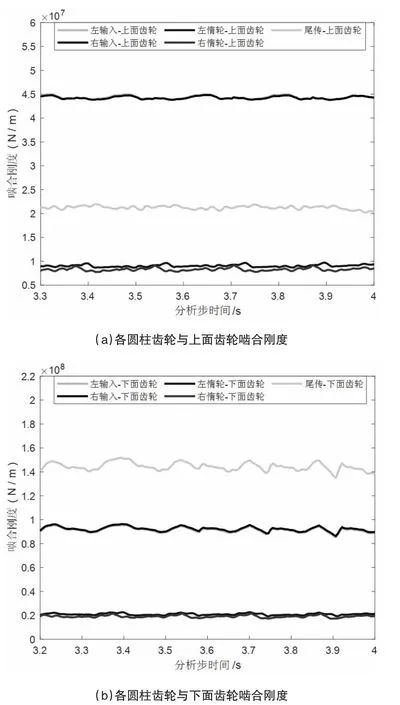
图5 面齿轮分扭传动系统啮合刚度

4 结论

建立了面齿轮分扭传动系统有限元仿真分析模型，推导得出了面齿轮副啮合刚度的解析计算方法，并计算得到了面齿轮分扭传动系统结构各齿轮啮合副的时变啮合刚度曲线，为后续的系统动力学分析提供了准确的刚度激励。