卷烟厂大空间厂房多空调系统相互耦合影响研究

张宇龙，代 军，孔 政，白庆华

(1.四川中烟工业有限责任公司绵阳卷烟厂，四川 绵阳 621000； 2.重庆大学能源与动力工程学院，重庆 400044)

0 引言

与住宅相比，大型公共建筑具有占地面积大、空间结构复杂等特点，维持日常运行所需能耗更高。根据2020年中国能源建筑报告[1]，2018年，全国建筑全寿命周期消耗能源总量占全国能源消费总量的比重为46.5%，其中运行阶段的能耗占到全国能源消费总量的21.7%。大空间空调不仅能效低，还存在室内气流组织复杂、室内温度场和速度场分布不均匀现象。在满足工业要求和舒适性的前提下，如何优化气流组织并实现节能减排是需要深入研究的问题。

目前的研究大多针对不同气流组织形式展开，包括上送风的全空间空调方式、侧送风的分层空调方式和下送风的局部空调方式。李彬[2]以体育馆为研究对象，采用计算流体力学方法，得到适合各种比赛的空调送风角度和送风速度，从而提高能量利用系数。杨睿康[3]建立了某高铁站候车厅的物理模型和温度梯度的分布函数，并用实测数据进行了验证，结果表明，采用下送上回的送风方式，温度预测模型符合精度较高。瞿北北[4]采用CFD方法对某动力电池厂房进行仿真分析，结果表明，增加送风口数量及优化风口的布置能够满足工艺生产要求及人体舒适性要求。Wang等人[5]建立了医院大楼的物理模型，采用CFD，分析了全空调和分层空调的室内舒适性，发现分层空调设计在6～18 m高的大厅中，其节能率可达19.7%～49.3%。

目前的研究主要是通过改变大空间空调的送风条件、送风方式，寻求最佳的气流组织形式，以满足大空间温湿度均匀性的要求，并对能耗及舒适性进行评价。研究大多针对同一参数的空调进行模拟分析，对同一大空间的不同空调之间的相互影响研究较少。而在同一区域内，相邻空调往往存在交叉影响，从而导致能耗增加，因此研究相邻空调的相互扰动情况对降低能耗具有重要意义。

针对四川某卷烟厂的卷接包车间，采用CFD，对多台独立空调作用下的气流组织及温度分布展开计算，通过构建交叉影响因子，考察单台空调工作的影响区域及作用程度，分析不同空调分区之间气流相互扰动的影响规律，评价其对空调系统能耗的影响，为无隔断的大空间内多空调系统节能优化提供理论支持。

1 模型建立

1.1 物理模型

研究对象为四川某卷烟厂的卷接包车间，根据厂房实际尺寸建立1∶1的车间模型[6]，其(长×宽×高)尺寸为99 m×60.8 m×6 m。东、南墙为内墙，外墙朝西、北两侧，北侧墙上设置有窗户。该车间内分布12台卷包机械，每台功率为60 kW，在模型中简化为12个长宽高分别为18 m×6 m×2 m的长方体。此外，东南角设有2台包装机械，每台功率为10 kW，将其简化为2个长宽高分别为13 m×6 m×2 m的长方体。大空间厂房采用4个风机盘管供应冷空气，每个风机盘管连接有48个圆盘形扩散风口，其尺寸为Φ403 mm。回风由12个双层百叶风口组成，其尺寸为1 000 mm×800 mm。简化后的模型如图1所示。

图1 卷接包车间简化模型Fig.1 Simplified model of cigarette making and tipping workshop

1.2 数学模型

大空间流体运动满足质量守恒定律、能量守恒定律和动量守恒定律，通过如下方程描述[7]：

质量守恒方程：

(1)

能量守恒方程：

(2)

动量守恒方程：

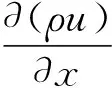
(3)

式中：ρ为密度；cp为定压比热容；u为流体速度分量；T为温度；γ为运动黏性系数；p为压力；fx为作用在x方向上的体积力；ST为源项。

1.3 边界条件

该模型中的热量来源主要为卷接机械与包装机械的功率及通过外墙、外窗和屋顶传入的热量。卷接机械、包装机械和外墙采用第二类边界条件，其热流密度大小分别为205.48 W/m2、64.94 W/m2、0.695 W/m2。由于现场工作人员较少，在此没有考虑工作人员的热负荷。外窗采用第三类边界条件，环境温度为32.8℃，传热系数为3 W/(m2·k)。屋顶采用第三类边界条件，环境温度为32.8℃，传热系数为0.552 W/(m2·k)。送风口为速度入口边界条件，速度大小为4.5 m/s，送风温度为18.1℃。为了更好地体现送风口旋流特性，采用风口动量模型[8]，将圆形风口八等分。根据叶片的倾斜角度为45°，分别算出x、y、z三个方向的速度大小。回风口采用自由出流边界。

1.4 网格划分与数值求解方法的选择

采用四面体网格进行网格划分，对送风口、回风口、热源及壁面附近的区域进行网格加密和网格无关性验证，整个卷接包车间的网格数量约为1 200万。

控制方程中对流项采用二阶迎风格式离散，压力项采用PRESTO!，其他项采用一阶迎风格式。大空间内气流组织流速低、温度分布均匀，满足Boussinesq假设，即仅考虑温度对空气密度的影响。由于大空间中空气密度基本保持不变，可将气流视为等温不可压缩流，而SIMPLE算法是适用于求解不可压缩流的有效数值方法[9]，因此使用SIMPLE算法可以满足要求。此外，在大空间建筑室内环境的数值分析中，Realizablek-ε模型由于考虑了气流的旋转效应[10]，适用于大空间气流流动的研究。采用标准壁面函数方程来计算贴近壁面空气的流动。

2 数值模型验证

选取卷接包车间夏季工况下的现场温湿度测点、数据进行模型准确性验证。对模型输入当天测得的送风温湿度，得到各个测点的仿真值，与现场的测点进行对比。结果如图2所示。

从图2可以看出，各测点实验值和仿真值吻合较好，整体平均误差约为6.05%，满足计算分析要求。

图2 实验与仿真结果对比Fig.2 Comparison of experiment and simulation results

3 数值结果与分析

3.1 全空调运行

为观察全空调运行情况下的温度分布和速度分布，将4台空调设置为相同的送风参数，即送风速度为4.5 m/s，送风温度为18.1℃，卷接包车间设计温度为(25±2)℃，通过仿真得到四台空调全开的情况下整个大空间内的温度场和速度场，选取Y=23.4 m的横截面(即风口所对应的截面)进行分析。全空调运行的流场及温度分布情况如图3所示。

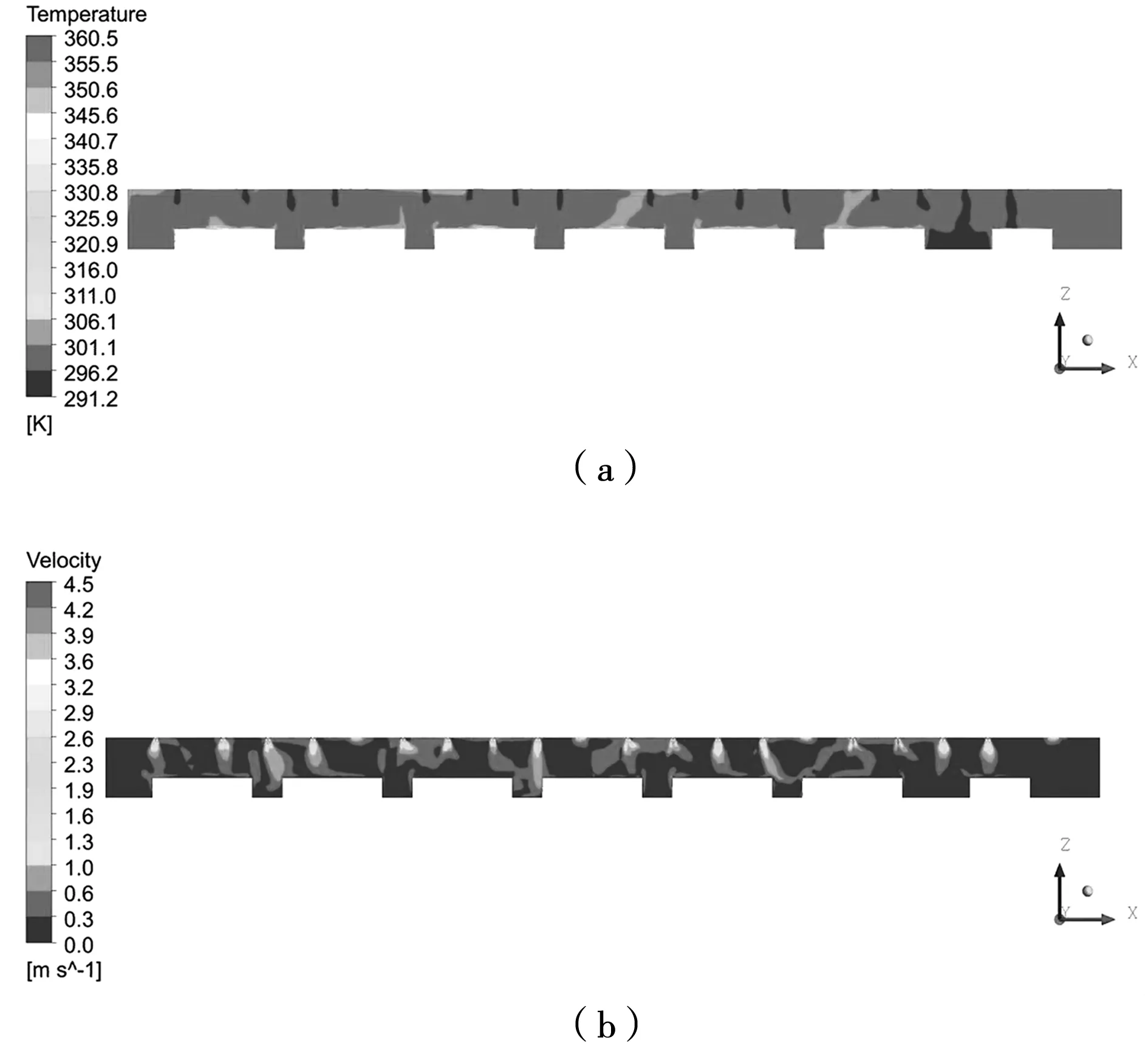
图3 全空调运行情况下温度分布和速度分布(a)温度分布;(b)速度分布Fig.3 Temperature and speed distribution under full air conditioning operation (a) temperature distribution; (b) speed distribution

从图3(a)可以观察到，在4台空调全开的情况下，车间平均温度为25.3℃，满足设计要求，但在热源附近表面温度偏高，其原因主要是设备上方的高温气流在上升过程中被向下流动的冷空气卷吸，随着送风射流回到设备附近。从图3(b)中可发现在空调的送风口附近的速度比较高。在竖直方向上的速度逐渐衰减，最终在近地面达到比较低的速度。竖直方向上的气流分布不均，竖直向下的气流出现了倾斜现象，这是由于射流的衰减作用及不同空调区域间的气流相互影响导致的，因此可以分析出相邻空调间存在气流扰动现象。

3.2 单台空调相互扰动影响

为了分析空调间的影响程度大小，通过仿真设置单台空调工作，观察其气流分布形态，分析其规律。如图4所示是单台空调工作时的流场。

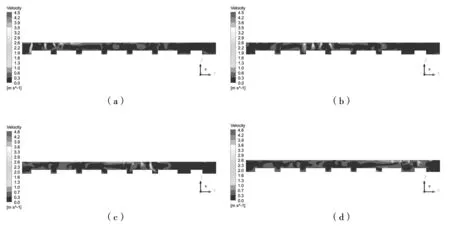
图4 单台空调工作时速度分布图(a)1号空调工作;(b)2号空调工作;(c)3号空调工作;(d)4号空调工作Fig.4 Speed distribution of a single air conditioner (a)No.1 conditioner; (b)No.2 conditioner; (c)No.3 conditioner; (d)No.4 conditioner

从速度分布图来看，可以观察到单台空调工作时，主要影响区域为工作空调所对应的区域，但也会对其他区域造成影响。从图中可以看出，1号空调工作时2号区域存在一定大小的速度分布。在2号空调工作时，1号区域和3号区域均存在可观的速度分布。在未开启空调区域存在气流分布的原因可能是开启空调区域的气流到了未开启空调区域[11]。

3.3 交叉影响因子

为了进一步分析气流分布不均产生原因并探究相邻区域的影响程度，引入空调间的交叉影响因子α。由于流速不具有叠加性，考虑采用大空间能量守恒来确定交叉影响因子。各相邻区域的关系如图5所示。以1号空调单台工作为例，仅考虑相邻空调(2号空调)的影响程度。在CFD模拟中可得到1号区域和2号区域的质量交换量m12。由此，1号空调对1号区域影响的权重因子如式4所示。

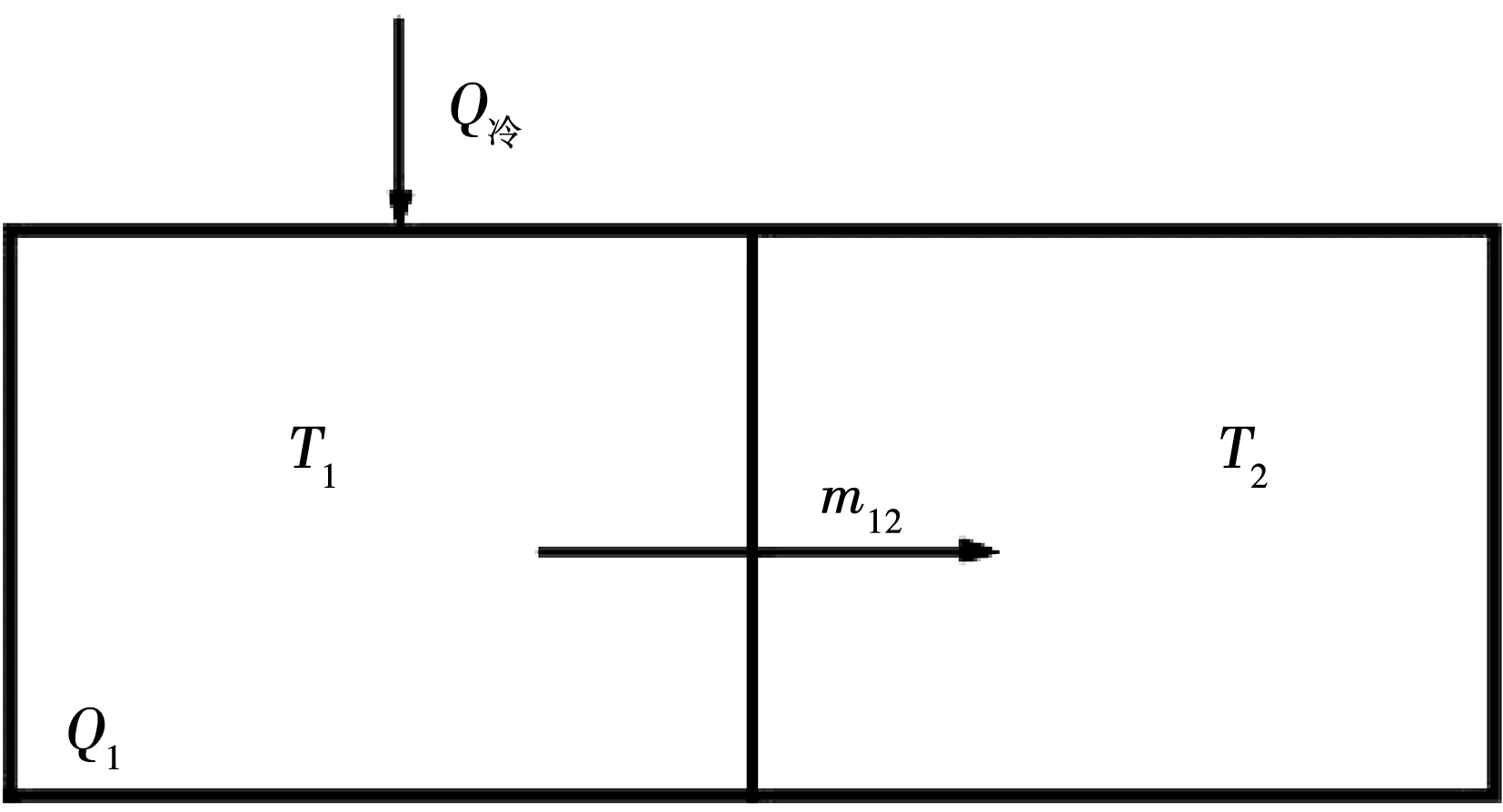
图5 1号空调相邻区域关系图Fig.5 Diagram of adjacent areas of No.1 air conditioner

(4)

Q1=cp(m总-m12)(T1-Tin)

(5)

Q冷=cpm总(Tout-Tin)

(6)

a2=1-a1

(7)

式中，cp表示定压比热容，Tin表示送风温度，Tout表示回风温度，Q冷表示空调冷负荷，Q1表示空调带走1号区域的热负荷。T1表示1号区域的平均温度，m总表示总的送风质量流量，α表示交叉影响因子，其物理意义可定义为某区域内由于空调作用所带走的热量占空调所带走总热负荷的比值。

通过仿真可得到Tin=291.3 K，Tout=320.4 K，m总=23.34 kg/s，T1=313.9 K，m12=0.12 kg/s，将数据带入表达式求得α1=0.77，α2=0.23。即可认为在1号空调工作时，对该区域的影响最大，即从1号空调送入的冷风对区域1的影响权重达到77%，而2号区域的权重为23%。发生气流相互影响是由于相邻区域没有隔断导致气流流动。同理可基于此模型，仿真在在4号空调运行时，计算得到权重因子分别为：α3=0.13，α4=0.87。

当空调3单独运行时，对相邻空调即2号和4号空调的影响程度，相邻空调能量关系如图6所示。存在以下关系式。

图6 3号空调相邻区域关系图Fig.6 Diagram of adjacent areas of No.3 air conditioner

(8)

Q3=cp(m总-m23-m34)(T3-Tin)

(9)

Q2=cpm23(T2-Tin)

(10)

Q4=cpm34(T4-Tin)

(11)

a2+a3+a4=1

(12)

a2∶a4=Q2∶Q4

(13)

通过带入仿真的数据，其中m23=0.12 kg/s，m34=0.17 kg/s，m总=23.34 kg/s，T2=322.4 K，T3=314.2 K，T4=318.2 K，tout=322.8 K，计算求得α2=0.17，α3=0.72，α4=0.11，由此可以得到，处于中间区域的3号空调将会对2号区域和4号区域的影响。3号空调影响该区域的程度达到72%，2号区域和4号区域分别为17%和11%。虽然2号与3号之间的质量流量要大于3号与4号之间的质量流量，但由于4号区域的打包机热流密度较小，该区域的平均温度较低，因此从3号区域进入到4号区域的冷风所吸收的热量较小。因此3号空调对4号区域的影响程度小于对2号区域的影响程度。同理可基于此模型，在2号空调开启时，计算求得α1=0.11，α2=0.74，α3=0.15。

4 优化及分析

对计算所得的交叉影响因子采用相互抵消的方式来确定空调间的影响程度，如1号空调对2号区域的交叉影响因子为0.23，2号空调对1号区域的交叉影响因子为0.11，最终叠加得到1号空调对2号区域的综合影响为0.12，即1号空调全负荷送风时，有12%的送风量被送到2号区域。另外可得3号空调对2号空调的综合影响为0.02，4号空调对3号区域的综合影响为0.02。因此在1号空调和4号空调送风量不变的情况下，各空调送风比例即为1:0.86:0.98:1。通过减小送风量来达到节能的目的，各台空调的送风量分别为原来的100%、86%、98%、100%。

为保证进行优化后，环境参数依然能够满足卷接包机正常运行的条件，对改变送风量前后卷接包机附件的温度场进行对比分析，如图7所示。选取1、4、5、8、9、12号卷接包机距x正方向1 m，高度为2 m，y方向上平均取3个点的温度对比实施节能前后对卷接包机工作的影响，如表1所示。

图7 1、2号卷接包机附近1 m的温度分布图(a)节能措施前；(b)节能措施后Fig.7 Temperature distribution 1 m nearby No. 1 and No.2 cigarette making and tipping machine

表1 卷接包机x正方向1 m处各特征点温度Tab.1 Temperature of different features in 1 m of x positive direction of cigarette making and tipping machine

由仿真结果计算得到节能措施前后距卷接包机x方向1 m处的各点温度最大差值为1.32 K，平均温差最大为1.12 K，能够满足卷接包机的工作环境。由此可见，在2号空调送风量减小14%，3号空调送风量减小2%的同时，对卷接包机的工作状况具有较小的影响。因此，通过计算相互空调区域之间的影响因子，在保证卷接包机正常工作的前提下，调小空调送风参数，能够达到节能的目的。

5 结语

以四川某卷烟厂的卷接包车间为研究对象，采用计算流体动力学方法，对大空间厂房全空调运行和单台空调运行时的气流组织和温度场分布情况进行计算分析，研究不同空调分区之间气流相互扰动的影响规律，提出了大空间空调的交叉影响因子。

结论如下：全空调运行时，大空间温度场分布相对比较均匀，平均温度为25.3℃，满足设计要求。1号空调单独运行时，对1号区域的影响权重为77%，对2号区域的影响权重为23%，在4号空调单独运行时，对4号区域的影响权重为87%，对3号区域的影响权重为13%。2号空调单独运行时，对1号区域的影响权重为11%，对2号区域的影响权重为74%，对 3号区域的影响权重为15%。3号空调单独运行时，对2号、3号、4号的影响权重分别为17%、72%、11%。通过计算减小2号空调14%的送风量、3号空调2%的送风量可满足卷接包机正常工作环境要求。