Stancu型q-Bernstein-Durrmeyer算子的统计逼近性质
任美英
(武夷学院 数学与计算机学院,福建 武夷山 354300)
自1997年Phillips[1]提出并研究q-Bernstein算子以来,q-微积分在逼近论中的应用成为一个研究热点,很多逼近论方向的专家学者致力于该领域的研究,研究成果较为丰富[2-5]。2019年,任美英研究Stancu型q-Bernstein-Durrmeyer算子的逼近性质,得到了算子列的一个Korovkin型收敛定理,并给出算子列收敛速度的一些估计[6]。
为研究Stancu型q-Bernstein-Durrmeyer算子的统计逼近性质,引入q-整数和q-微积分的若干概念[7-8]。对任意固定的实数q>0和非负整数k,q-整数和q-阶乘分别定义为:


Beta函数的q-模拟定义为:

其中:α,β是给定的两个实参数,满足0≤α≤β。
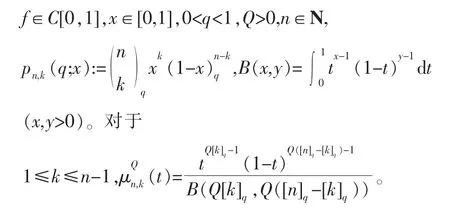

1 引理
为了研究的需要,引入几个辅助结论。

2 统计逼近

注意:任何收敛数列是统计收敛的,但反之不然[12]。
设B[a,b]表示定义在区间[a,b]上的所有有界函数的集合,C[a,b]表示定义在区间[a,b]上的所有连续函数的集合。
2002年,Gadjiev和Orhan将统计收敛概念应用到逼近理论中,得到了如下关于统计收敛的Bohman-Korovkin型逼近定理[13]。
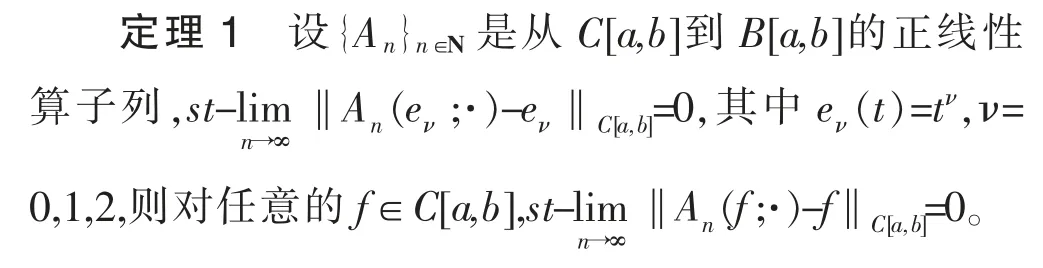
设序列q={qn},0<qn<1满足条件:

下面给出Stancu型q-Bernstein-Durrmeyer算子的统计逼近定理。
定理2 让序列q={qn},0<qn<1满足条件(5),则对任意f∈C[0,1],有

证明 由Stancu型q-Bernstein-Durrmeyer算子和q-Jackson积分的定义知,对任意f∈C[0,1],是从C[0,1]到C[0,1]的正线性算子列。对eν(t)=tν,ν=0,1,2,由(2)式,显然有
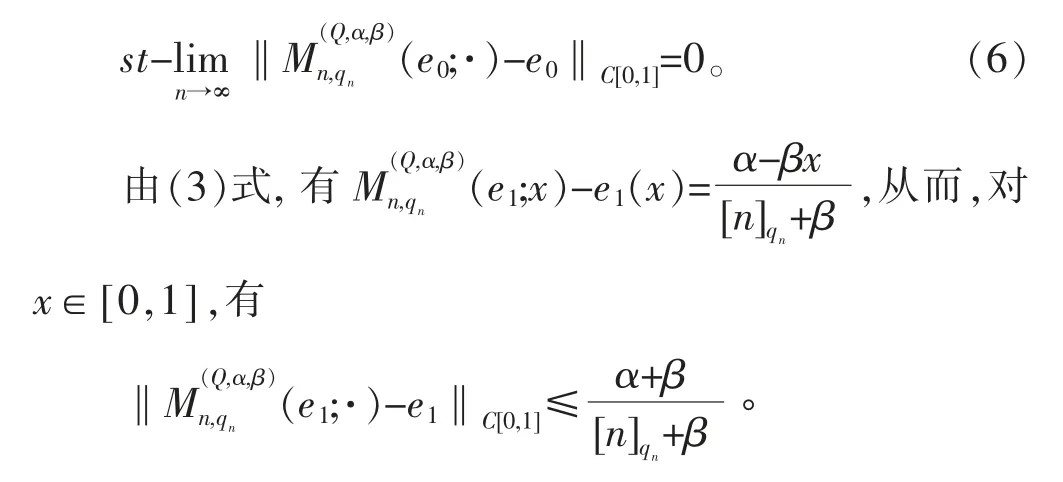
对任意给定的正数ε,令


综合(6)式、(8)式和(10)式,由定理1可知,所述的结论成立。
3 统计收敛速度
对f∈C[0,1]和δ>0,f的连续模定义为:
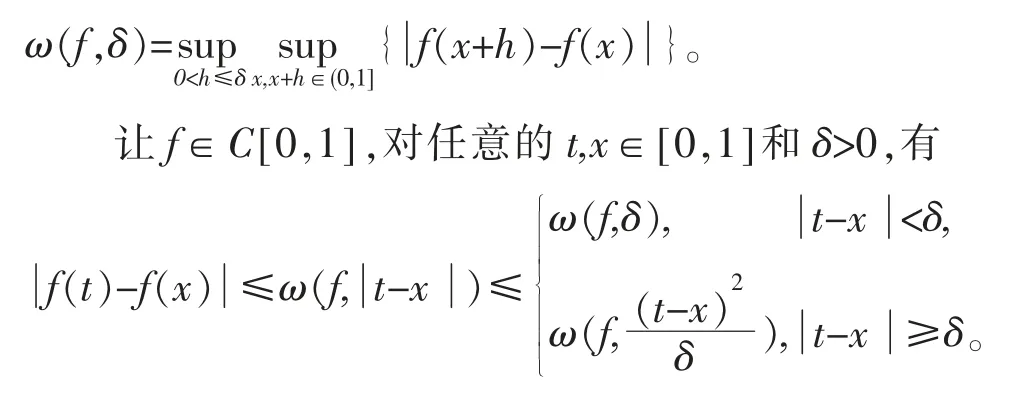
又因为对λ>0,有ω(f,λδ)≤(1+λ)ω(f,δ),所以,对任意的t,x∈[0,1]和δ>0有
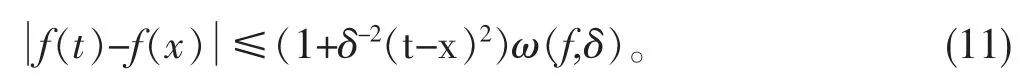
下面将借助连续模,给出Stancu型q-Bernstein-Durrmeyer算子的统计收敛速度。
定理3 让序列q={qn},0<qn<1满足条件(5),则对任意f∈C[0,1],有其中


