基于全信息初值优化的GM(1,1)模型在物流行业中的应用

□ 严亚波

(江南大学 商学院,江苏 无锡 214122)

1 引言

灰色系统理论[1]自1982年问世以来，就因在研究“小数据”“贫信息”等不确定性问题时具有优势而广受关注。灰色预测模型理论是研究最活跃、应用最广泛的灰色系统模型之一，灰色预测是一种时间序列预测方法，该方法的优势在于建模数据量小，建模过程简单，因而被广泛研究。其中，GM(1,1)模型是灰色预测理论中最核心的模型，是灰色模型中的基础，也是被研究次数最多、应用最广泛的灰色预测模型，并衍生出诸多变种。学者们从应用以及优化等多个方向对GM(1,1)模型进行了深入研究。

近年来，GM(1,1)模型在诸多领域得到了广泛的应用。卢捷、李峰将初始值和背景值看作变量，对经典GM(1,1)模型背景值与初始值进行改进,提出了一种初始值和背景值组合优化的方法[1]；罗党、王小雷在灰色预测模型中引入三角函数，由此提出了耦合结构的灰色GM(1,1,T)模型，然后利用Levenberg-Marquardt算法求解模型结果[2]；刘震、谢玉梅、党耀国建立脱贫攻坚理论模型,分析政策性扶贫的外生性影响，而后依据脱贫规律对GM(1,1)模型进行改进,构建脱贫进展预测模型[3]；亢玉晓、肖新平研究GM(1,1)多种不同衍生模型的缺陷，并对其差异性进行分析[4]；吕海涛、程帅帅、吴利丰等基于残差尾段的强(弱)化缓冲算子还原模型，拓展了模型的建模应用范围[5]；张福平、刘兴凯、王凯建立研究生规模的灰色模型对毕业人数、招生数以及在校学生数规模进行预测[6]；李翀、谢秀萍考虑系统时滞的动态变化效应，提出以灰色关联理论为基础的时变时滞函数的参数优化方法[7]；李丽、李西灿定义了背景值系数序列，并推导了GM(1,1)灰微分方程的解的表达式，然后利用优化算法求解准光滑数列的最佳背景值系数，来提高GM(1,1)模型的精度[8]；丁松等通过对原始序列加权，在考虑新信息优先的基础上优化初始条件，构建了全信息初始条件优化的非等间距GM(1,1)模型[9]；江艺羡、张岐山利用黎曼积分推导出了以不规则梯形面积取代传统梯形面积构造法，以此优化了传统GM(1,1)模型背景值[10]；Xiao X P、Guo H、Mao S H运用矩阵分析思想对GM(1,1)模型的建模机理进行分析，提出了基于分数阶累积生成的GGM(1,1)模型的可拓形式，分析了其理论意义[11]；Ceylan Z、Bulkan S、Elevli S对自回归综合移动平均法(ARIMA)、支持向量回归法(SVR)、灰色建模法(1,1)和线性回归法(LR)等各种数学建模方法在预测土耳其最大城市伊斯坦布尔医疗废物产生方面的效果进行评估[12]；Shen Q Q等基于新的信息优先级原则和分数累积生成算子的思想，提出了一种新的加权分数GM(1,1) (WFGM(1,1))预测模型[13]；Wang Q、Song X提出NMGM (1,1,alpha)，通过有效地结合非线性预测技术和生物代谢思想，将非线性灰色模型(GM)从静态模型升级为动态模型，并预测中国石油消费[14]；Zeng B、Li C提出了一种自适应智能灰色预测模型，与传统灰色模型结构固定、适应性差的缺点相比，该模型可以根据建模序列的真实数据特征自动优化模型参数[15]；Wang Y等通过对原始序列第一个分量和最后一个分量进行加权来优化初始条件以提高GM(1,1)模型预测精度的新方法，利用最小误差平方和法求解组合中第一项和最后一项作为初始条件的加权系数[16]；Lu Y、Xie N、Wei B等提出了一个统一的框架，从积分-微分方程的角度重建了统一的非线性灰色系统模型，并将该模型应用于长三角城市污水排放和用水量预测中[17]；Tong M Y从传统GM(1,1)模型的背景值入手，采用外推法对模型进行扩展，提出了一种优化的灰色预测模型，采用模拟退火算法求解模型[18]；Zeng Bo等对物理指标的数据特征进行了系统的分析，应用具有这些特征的数据专用的灰色系统模型，对人体指标的变化趋势进行了模拟和预测[19]；丁松等按照信息充分利用以及新信息优先等原理对模型初始条件进行优化，然后提出了一种初始条件和幂指数组合优化的方法[20]。

通过对以往文献的分析研究，可以发现传统GM(1,1)模型的初始条件为序列的第一个分量x(1)(1)[21]，但是初始序列距离系统较远，影响有限，而对系统影响较大的新信息的作用却常常被忽略，因此存在一定误差；此外，也有专家学者基于新信息有限选择最后一个分量x(1)(n)作为初始条件[22]，虽然在一定程度上利用了新信息，但只考虑新信息对系统的影响而忽略旧信息的作用，同样会影响模型精度；还有部分学者选择以二者线性组合来优化初始条件，然后利用算法等进行求解[20]，该方法虽然由旧信息和新信息组合来优化，但没有充分考虑不同信息对系统的影响程度不同，对于“数据量小”的灰色预测模型来说，势必不能够对有效信息进行充分提取，造成信息的浪费，从而影响GM(1,1)模型建模效果。本文对模型的改进也将从这个角度展开。

文献[20]根据新信息优先原理，对原始数据的每一个量进行加权优化初始条件，通过设置权重系数来表现新旧信息在初始条件构建中作用大小的变化规律，以充分提取原始序列中对系统发展预测有效的信息，充分利用旧数据的经验知识和新数据的趋势信息，综合考虑新旧信息间的权重分配关系，来构建新的初始条件。本文在文献[20]的基础上，将该初值优化方法引入到GM(1,1)模型优化中，构建了基于初始条件优化的GM(1,1)模型，并利用该模型对我国物流行业发展规模进行预测。

2 GM(1,1)模型的基本形式

GM(1,1)模型是灰色系统中最基础的模型，同时也是最重要且应用范围最广的模型。GM(1,1)模型中第一个“1”意为一阶方程，第二个“1”意为单变量。本节将重点介绍传统GM(1,1)模型的建模机理。

设非负原始序列为X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，对原始序列X(0)作一阶累加生成(1-AGO),得到序列：

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

对序列X(1)作紧邻均值生成，得到序列：

Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))

其中，z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),k=2,3,…,n。

定义2.1：设X(0)为非负原始数据序列，X(1)为X(0)的1-AGO序列，Z(1)为X(1)紧邻均值生成序列，则有称

x(0)(k)+ax(1)(k)=b

(1)

为原始GM(1,1)模型，

x(0)(k)+az(1)(k)=b

(2)

为具有背景值的GM(1,1)模型。

定义2.2：设a为发展系数，b为灰作用量，则称

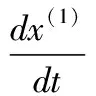
(3)

为GM(1,1)模型的白化方程。

(1)白化方程的时间响应函数表达式为

(4)

(2)在初始条件x(1)(t)|t=1=x(1)(1)时的时间响应式为

(5)

(3)还原值为

(6)

上述为传统GM(1,1)模型的建模机理，由于该模型应用十分广泛，由此可以演化出多种不同的GM(1,1)模型，如EGM(1,1)模型、DGM(1,1)模型、SGM(1,1)模型等。传统模型虽然应用广泛，但仍有较大改进空间。

3 优化的GM(1,1)模型构建及参数求解

为了对系统有效信息进行充分提取，提高建模精确度，本节将采用全新的方法对GM(1,1)模型初始条件进行优化，并研究相关参数的求解路径。

3.1 基于全信息初值优化的GM(1,1)模型

在实际建模过程中，GM(1,1)模型的预测精度不该只和原始序列的第一个分量x(1)(1)或者最后一个分量x(1)(n)有关，而是与X(1)的每一个分量都存在一定的关系。新信息优先原理提出，新信息对系统发展趋势变化的影响更大，因而在建模过程中对系统未来发展的预测作用远大于离系统较远的旧信息，所以在初值构建过程中新信息应当被赋予更大的权重。但这并不意味着旧信息就应当被摒弃，尽管旧信息的预测效用较低，但依据信息充分利用原理，旧信息也不应被摒弃，而是充分利用其中残存的有用信息来进一步提高模型精度。因此，在建模过程中要对新旧信息进行权重分配使得权重能够准确反映信息对初始条件的实际影响大小，能够有效地提高灰色预测模型的建模精度。因此，在充分考虑新旧信息的预测效用的情况下，引入一个权重系数λn+1-k(0<λ<1)，k=1,2,…,n，以X(1)的所有分量的加权组合来构建初始条件，从而对灰色GM(1,1)模型进行优化，即以

(7)

为初始条件。权重λn+1-k(0<λ<1),k=1,2,…,n将随着时间的推移而递减，分量越靠后则权重越大，且其递减速度与λ取值相关，λ取值越小，递减越快，反之越慢，如图1所示，图中横坐标表示λn+1-k随着幂指数增加而变化，在λ的不同取值下，λn+1-k变化情况如图所示。λn+1-k一定程度上揭示了原始序列的每个分量作用随着时间的推移在不断增加。权重系数的选择主要由数据序列的实际意义所决定，而非人为设定。从图1可以看出，λk-1<λk-2<…<λk+1-n满足序列的权重随着信息的新旧程度由旧到新不断增加，且序列的所有分量对系统的影响实际效用均被考虑到，构建的新初值既满足新信息优先原理又满足信息充分利用原理。

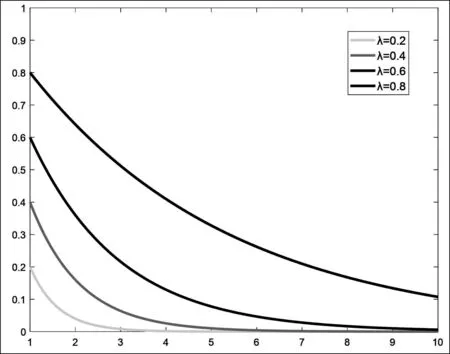
图1 不同λ取值对应权重系数变化趋势

(8)

(9)

(2)还原值为

(10)

如此便得到基于全信息初值优化的GM(1,1)模型，记为PIGM(1,1,λ)。

3.2 基于全信息初值优化的模型参数求解

通过基于初值优化的GM(1,1)模型的建模机理可知，我们只要确定了初值参数φ，便可实现基于初值优化的GM(1,1)模型模拟和预测，因此，对于初值参数φ的求解是至关重要的一步。本节将通过建立非线性优化模型，借助matlab软件，求解模型的最优初值参数。

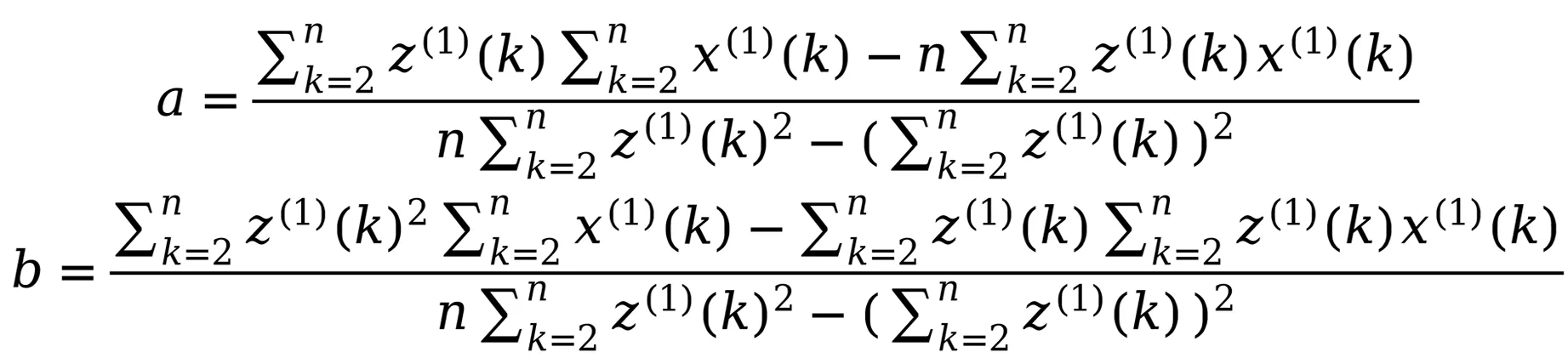
为了统一参数优化的目标函数与预测结果检验准则，本文选择平均相对误差最小化为目标，将初值、系统参数a和b、背景值等表达式作为约束条件，建立式(11)的非线性优化模型：

(11)

通过智能软件matlab可以很方便地求解出初值参数φ以及参数a和b，将求得的初值x(1)(φ)代入式(10)中，便可求得权重系数λ的取值。所有参数均求解出来后，便可根据定义3.1.1进行模型的模拟和预测，最后实现基于全信息初值优化的GM(1,1)模型构建与应用。

4 实例分析

物流是指通过运输工具实现物品在不同区域流动的过程，是将包装、装卸、搬运、储存、流通加工、运输、配送等基本功能有机结合以实现资源的合理配置及优化。随着电子商务的发展，国内物流基础设施布局也已完善，物流与电子商务密不可分，已经成为国民经济发展中的关键环节之一，连接社会经济的各个部分并使之成为一个有机整体，是国民经济和社会发展的重要组成部分。我国物流行业经过多年的快速发展，目前已步入高质量发展的阶段，扩张速度逐渐放缓。

2020年，全国社会物流总额约为300.1万亿元，但增速相较于2019年回落2.4个百分点，增速逐渐放缓。而从构成看，工业品物流占比接近90%，总额约269.9万亿元，按可比价格计算，同比增长2.8%。除工业品物流外，农产品物流、单位与居民物品物流、进口货物物流以及再生资源物流约占10%。其中，农产品物流总额4.6万亿元、单位与居民物品物流总额9.8万亿元、进口货物物流总额14.2万亿元、再生资源物流总额1.6万亿元。本文选取我国2011-2017年的数据进行建模，然后选择移动平均法以及指数平滑法作为对照组来验证本文所优化的模型的准确度，如图2所示。

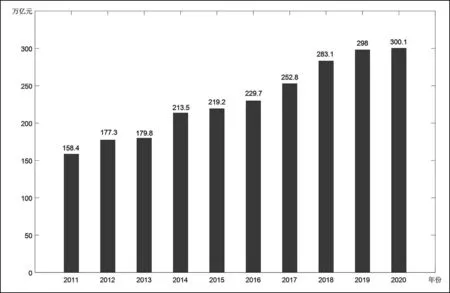
图2 2011-2020年我国社会物流总额变化图

具体建模过程如下：

原始数据为

X(0)={158.4,177.3,179.8,213.5,219.2,229.7,252.8}，

一阶累减生成序列为

X(-1)={158.4,335.7,515.5,729,948.2,1177.9,1430.7}，

均值生成序列

Z(1)={247.05,425.6,622.25,838.6,1063.05,1304.3}

各模型结果如表1和图3所示。

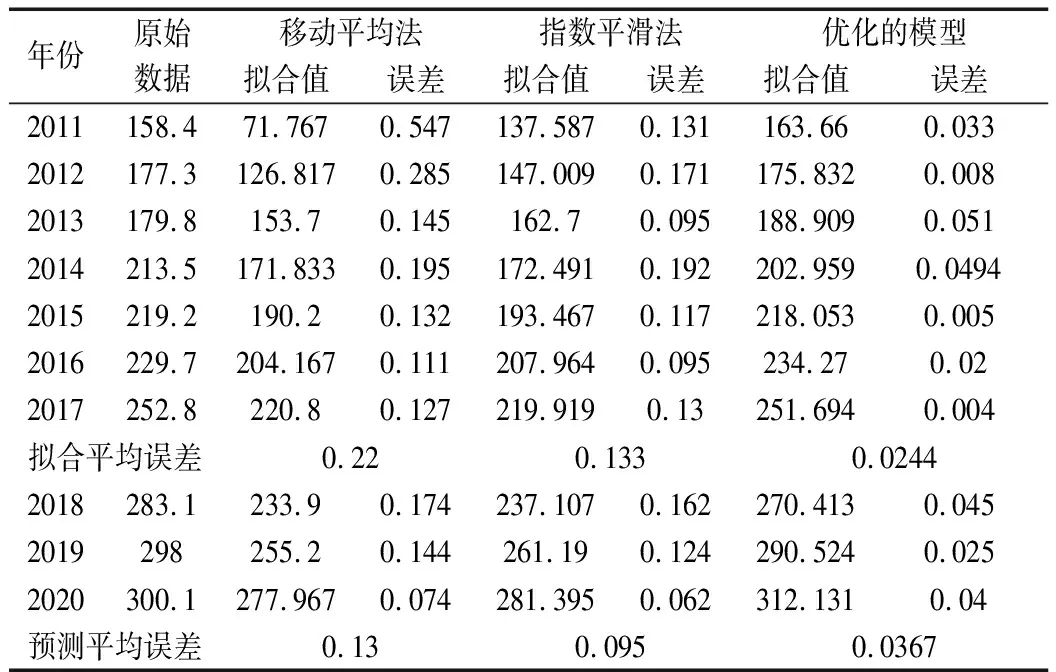
表1 三种模型的预测对比

图3 三种模型预测对比图

可以看出，本文所构建的模型无论是拟合精度还是预测精度都远高于对照组模型，模型的拟合精确度高达97.56%，预测精度高达96.33%，适合用于我国社会物流总额的预测。

5 结论

自灰色系统理论被提出以来，灰色预测模型作为灰色预测理论的核心和基础之一，在广大学者的不断研究与探索中变得越来越完善，也在实践检验的过程中逐渐得到了认可和广泛应用。在现有研究中，关于GM(1,1)模型的建模优化的研究已有不少，对于GM(1,1)模型优化的研究大都聚焦于初值的选择、背景值的构造、灰导数的构造、模型计算方法的改进等方向，但是对于全信息初值的构造却不多见。

本文在前人研究基础之上，基于初值方向，对GM(1,1)进行了优化。在初值的选择上，构建了全信息初值，充分提取了系统的有效信息，从而有效地提高了模型的预测精度。此外，我们将就全信息初值优化的GM(1,1)模型成功地应用于我国社会物流总额的预测中，分析了我国社会物流总额由慢速增长到快速增长，然后再到慢速增长的发展趋势，并对我国社会物流总额后续发展情况进行了预测，为相关部门制定发展规划提供政策决策依据。

相较于传统GM(1,1)模型以及前人基于单个方向对于GM(1,1)模型的优化，本文提出的全信息优化方法有效地提高了灰色GM(1,1)模型的精度，但是本文所构建的模型仍然只适用于短期预测，而不适用于中长期预测。此外，对于GM(1,1)模型的优化，除了全信息初值以外，还有其他优化方法以及组合方式，这些都是本文今后可以展开研究的方向。