基于KIVA机器人的紧致型仓储系统待命位策略研究

□ 王 婧,孙子文

(武汉科技大学 恒大管理学院，湖北 武汉 430065)

1 引言

随着城市人口密度越来越大，土地资源也越发紧张，高昂的土地成本持续促进仓储系统发展；同时，电子商务蓬勃发展，呈现出批量小、品类多、海量化、注重实效以及实时变化等特点，对仓储系统提出了更高的要求。如何在保持较高空间利用率的情况下，兼顾期望取货时间以及订单响应速度，是自动化仓储系统发展需要解决的重要问题。目前，关于仓储管理的研究越来越多，且越来越集中在紧致化和智能自动化仓储系统上。从采用自动牵引小车AGV的智能仓储系统[1]，到亚马逊推出的KIVA机器人系统[2],这类物至人拣货系统由于具有较高的取货率，经过多年的发展，已经成为物流业智能仓储系统主要的取货方式之一[3]。KIVA系统虽然极大地缩减了取货时间并提高了取货率，但是其空间利用率较低，在此基础上，Gue等[4]提出了一种高密度仓储系统，极大提升了空间利用率，但取货时间较长。

在传统的仓储系统中，一般采用的是人至物的取货流程，即拣货人员从I/O点出发，到达目标取货点取货并返回出库点，这种取货方式的取货时间大部分花在了取货人员的行走上[5]，而在智能仓储系统中，通过KIVA机器人或AGV取货的物至人取货系统，可极大缩减取货时间，并提高取货率和准确度[6]。为了进一步提升智能仓储系统的效率，许多学者对智能机器人的待命位进行了优化。Egbelu和Wu通过系统仿真的方法，比较了两种不同仓储方式下多个待命位策略的取货效率[7],徐贤浩、郭依等以取货时间最小化为目标，提出了三种待命位策略，并比较了三种不同待命位策略的优劣[8]。

现阶段,以KIVA机器人系统为基础的自动化智能仓储系统都具有较高的取货率，但其空间利用率较低。相比KIVA系统，Gue提出的网格仓储系统有着较高的空间利用率，但随着仓储规模的扩大，其取货效率逐渐降低，订单反应时间也在增加。电子商务发展到今天，各种电商企业的仓库对自动化智能仓储系统各方面的要求越来越高，小批量的订单、海量化的品类、昂贵的土地成本等因素都要求仓库必须提升空间使用率，注重订单时效及顾客满意度等因素都需要智能仓储系统降低取货时间、提高取货效率。因此，本文基于KIVA机器人系统提出了一种紧致型仓储系统，在考虑空间利用率的情况下，兼顾降低取货时间和提高取货效率，并比较不同待命位策略下的取货时间以及不同系统的空间利用率和系统容量。

2 问题描述

本文提出的紧致型自动化仓储系统布局如图1所示。在此系统中，取货与补货等操作都由KIVA机器人完成，相比于人工操作，缩短了取货时间，提高了精确度，降低了人工成本。该系统一次完整的取货周期如下：处于待命位的机器人收到取货指令后，从待命位出发行驶至目标货架，同时仓库内帮助进行翻箱操作的机器人同时移动，并进行翻箱操作，机器人将目标货架取出，送至取货口，拣货员在出货口完成拣货操作后，机器人将货架送回原位，最后机器人回到待命位等待下一个取货指令。

图1 紧致型仓储系统布局示意图

此系统布局与KIVA系统布局相似，有多条纵向通道，但为提升空间利用率，系统中只设置了两条横向通道，机器人在通道内行驶取货。本文研究了此系统的三种待命位策略：①取货完成并返还货架后机器人返回待命位I1点；②取货完成并返还货架后机器人返回待命位I2点；③取货完成并返还货架后机器人直接停留在原处。

3 模型构建

3.1 模型假设及符号说明

基本假设：①有足够多的机器人保证翻箱操作及取货操作的流畅性，机器人的数量不作为制约取货时间的因素；②在此系统中，机器人若要取内层货架，则需要进行翻箱操作，因本文假设有足够多的机器人辅助进行翻箱操作，故不考虑翻箱操作所花费的时间；③每一个货架被取到的概率都相等，即采用随机仓储策略；④忽略机器人转向时间以及举起和放下货架的时间；⑤机器人的行走速度比人的移动速度快，且匀速移动，不考虑加速和减速的影响；⑥图1中I1和I2既是待命位，也是出货口。

符号说明如表1所示。

表1 符号说明

3.2 待命位在I1点的平均取货时间模型

本文以子模块列数为6的紧致型仓储系统为例。在待命位为I1点的待命位策略下，一次完整的取货流程为：KIVA机器人收到取货指令后向目标货架移动，完成取货并返还货架，最终返回待命位。在此取货过程中，KIVA机器人进行了4次横向移动和4次纵向移动，且每次纵向移动时间相同，横向移动时间也相同，用Tx1表示每次横向移动的时间，用Ty1表示每次纵向移动的时间，则总的取货时间可以表示为

T1=4Tx1+4Ty1

(1)

建立一个如图1所示的直角坐标系，假设I1的坐标为(M1,0)，则横坐标的值为M1=ndl+6nb，假设目标货架M的坐标为Mi,j，其中i,j分别表示货架的行数和列数，此时可得到机器人的每次横向平均移动时间为：

(2)

将公式(2)化简后可得：

(3)

KIVA机器人在纵向移动过程中，由于任意一行货架到出货点的垂直距离都相等，因此当行数确定时，每一次纵向移动时间可表示为

(4)

将公式(3)(4)带入公式(1)，则可得到在此待命位策略下总的取货时间：

(5)

3.3 待命位在I2点的平均取货时间模型

T2=4Tx2+4Ty2

(6)

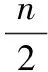
(7)

由于纵坐标未改变，KIVA机器人的纵向移动时间与第一种策略相同：

(8)

将公式(7)(8)带入公式(6)，可得到第二种待命位策略下的平均取货时间：

(9)

3.4 第三种待命位策略下的平均取货时间模型

分析以上两种待命位可知，第二种待命位策略即待命位在I2时，取货时间相对较短，所以应选取I2点作为第三种待命位策略的待命位点和出货口。在此待命位策略下，一次完整的取货流程：KIVA机器人收到取货指令后向目标货架移动，完成取货并返还货架，最终停留在货架返还处。在此取货过程中，KIVA机器人进行了3次横向移动和3次纵向移动，且每次纵向移动时间相同，横向移动时间也相同，用Tx3表示每次横向移动的时间，用Ty3表示每次纵向移动的时间，则总的取货时间可以表示为

T3=3Tx3+3Ty3

(10)

将公式(7)和(8)带入公式(10)，得到第三种待命位策略下总的取货时间：

(11)

4 数值实验与结果分析

4.1 模型验证

为了验证模型的有效性，参考徐贤浩等[8]研究的仓储系统，假设紧致型仓储系统中的基本参数为a=1.5,b=3,dl=1.2,dw=1.2。鉴于紧致型仓储系统的布局特点，可通过同时改变纵向通道数量、货架行数来改变系统规模的大小。在此基础上，设置1、2、3三种不同的场景，并在计算机中对三种不同的场景分别进行模拟取货操作，每次模拟进行200次取货操作，共模拟N次，最后计算模拟结果的平均值，并将其作为总的取货时间，可得到三种待命位策略的模型结果与仿真结果，如表2所示。

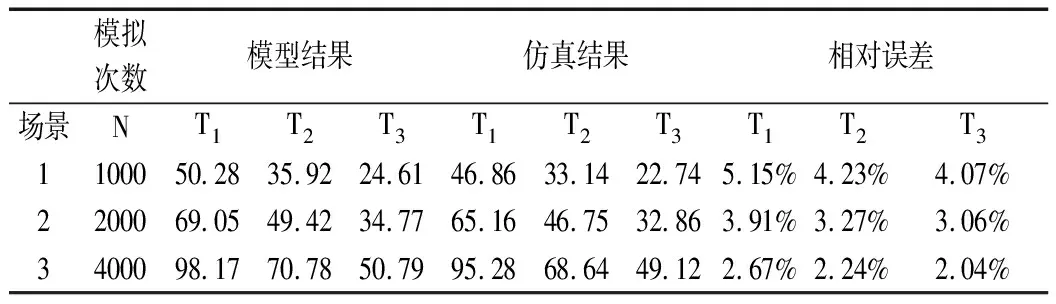
表2 模型结果与仿真结果

由表2可知，紧致型仓储系统在三种不同待命位策略下，KIVA机器人取货时间的模型结果与仿真结果的相对误差较小，最高只有5.15%，并且随着模拟次数的增加，相对误差也在缩小，因此模型的有效性得到了验证。

4.2 结果分析

改变系统面积，对本文提出的紧致型仓储系统与传统布局KIVA系统中的机器人平均取货时间进行研究，然后通过MATLAB模拟仿真，得到两种系统在三种不同待命位策略下的平均取货时间，如表3所示。

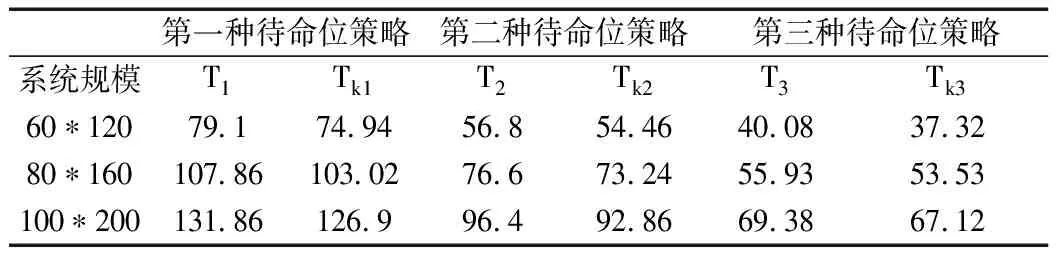
表3 三种待命位策略下紧致型仓储系统与KIVA系统的平均取货时间

在表3中，T1、T2、T3分别表示三种待命位策略下紧致型仓储系统的平均取货时间，Tk1、Tk2、Tk3分别表示三种待命位策略下KIVA系统的平均取货时间。观察表中数据可知，紧致型仓储系统的平均取货时间比KIVA系统要多2s到5s，这是因为当系统容量较小时，即使有翻箱机器人辅助进行翻箱操作，翻箱时间还是会影响取货时间，但当系统容量逐渐增大时，翻箱时间对取货时间的影响可以忽略不计，紧致型仓储系统的平均取货时间将与传统的KIVA系统的取货时间相同。

除了取货时间及取货效率以外，仓储系统的空间利用率、系统容量也处于重要地位，因此，对两种系统的空间利用率及系统容量进行比较是很有必要的。同时，由于仓储系统的空间利用率及系统容量取决于系统布局，待命位点的设置对其影响甚微，因此不用考虑待命位策略，可以直接进行比较。如图2所示，紧致型仓储系统和KIVA系统的空间利用率分别为81%和56%左右，前者空间利用率比后者高出将近25%左右；其次，如图3所示，当系统规模相同时，KIVA系统的容量是小于紧致型仓储系统的，并且系统容量的差值随着系统规模的增大而增大。

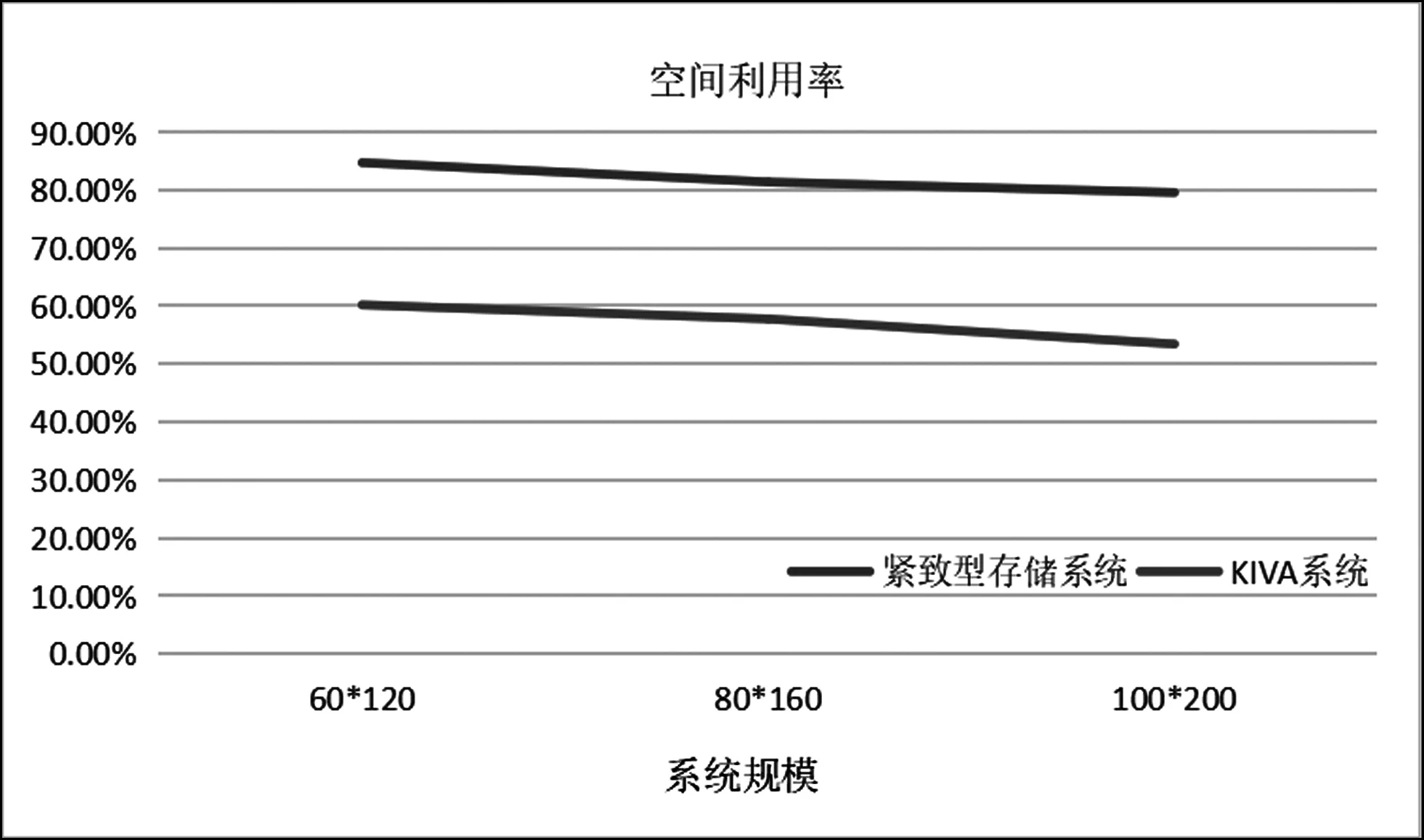
图2 空间利用率比较

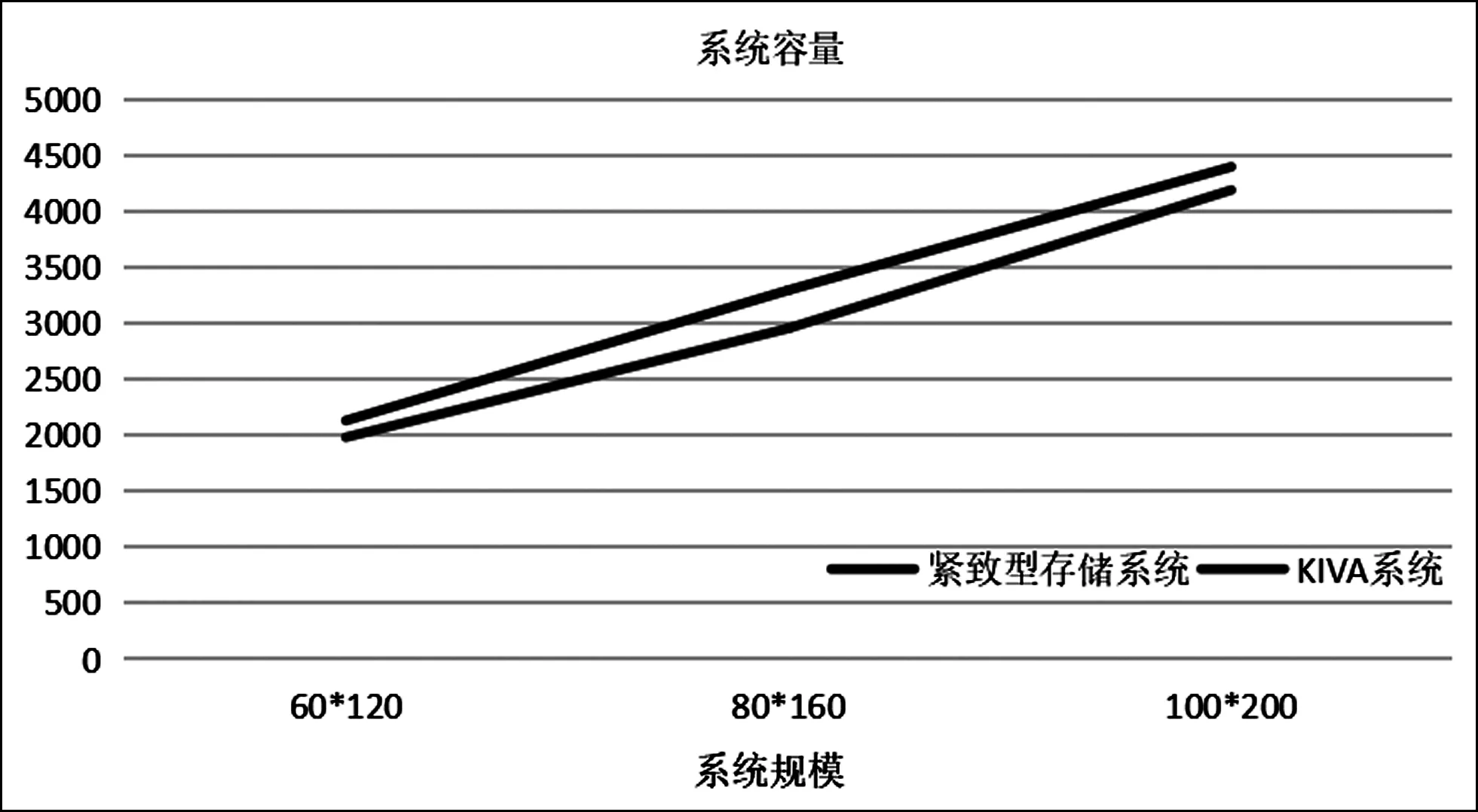
图3 系统容量比较

此外，由T1

5 结论

本文在KIVA机器人智能仓储系统基础上提出了一种紧致型仓储系统，并根据三种不同的待命位策略分别建立了取货时间模型，验证了模型的有效性。通过对紧致型仓储系统和KIVA机器人系统在三种不同待命位策略下的取货时间、系统空间利用率以及系统容量进行比较，发现紧致型仓储系统各方面性能均优于KIVA系统。然而，此系统需要较多数量的机器人进行翻箱和取货操作，这会提升机器人采购成本，不过随着科技进步，机器人的制造成本必定会逐渐下降，而土地成本和人工成本将来会越来越高，综合来看，基于KIVA机器人系统的紧致型智能仓储系统相对于传统的KIVA机器人系统会为企业节省更多的成本。因此，基于KIVA机器人的紧致型智能仓储系统有一定的现实意义。本文只研究了一个待命位的不同策略，也并未考虑机器人取货排队及拥堵问题，未来可以研究多个待命位同时取货以及排队等问题。