基于第一性原理的固体界面摩擦学性能高通量计算研究

何文豪, 鲁志斌*, 范晓丽, 周 峰, 刘维民

(1.中国科学院兰州化学物理研究所 固体润滑国家重点实验室, 甘肃 兰州 730000;2.西北工业大学 材料学院 先进润滑与密封材料中心 凝固技术国家重点实验室, 陕西 西安 710000)

摩擦学综合了物理学、化学、材料科学和力学等学科领域，主要研究相对运动或有相对运动趋势的界面间的摩擦、润滑和磨损行为及其机理.影响界面摩擦性能的因素是多方面的，主要包括界面性质、负载、服役环境和服役温度等.正是因为人们需要综合考虑各种因素来理解摩擦，从非常小尺度下的量子相互作用(界面的电子结构、吸附等)到大尺度下的宏观变量(负载、服役温度等)，这使得摩擦学的研究几乎不可能没有计算机模拟技术的辅助.在过去的几十年里，随着计算机硬件的持续发展，计算机模拟技术逐渐成为推动摩擦学发展的关键技术之一.

计算机模拟方法主要包括基于密度泛函理论(DFT)的第一性原理方法、分子动力学方法(MD)和有限元分析(FEA)方法等.这些方法在不同的尺度上对理解材料性能都起到了重要作用.尽管对摩擦性能的研究来说，DFT方法限制了界面结构(局限于无限平坦的界面)，但它可以深入到量子尺度，从界面电子结构的角度理解摩擦[1-5].据此，作者所在课题组提出了一种实现超滑的新策略-压力诱导超滑[6].科研人员也通过DFT方法解释了许多摩擦试验现象，比如界面钝化对金刚石[7-8]、类金刚石[9]、MoS2[10]和 Fe[11-13]摩擦 性 能的影响.这使得DFT方法成为理解摩擦性能和解释摩擦试验现象的重要技术手段.

近年来，在材料科学领域，高通量DFT计算模拟研究越来越普遍[14].兰州化学物理研究所周等[15]提出了离子液体和酯类化合物两类润滑剂物性参数和摩擦系数的高通量分子动力学计算框架.意大利摩德纳大学的Pizzi等[16]基于“自动化交互基础设施和数据库的计算科学框架”(AiiDA)，提出了第一个固体界面摩擦学性能的高通量DFT计算方法[17].尽管这个方法实现了固体界面的势能面(PES)和理想剪切强度(τ)的计算，但是该方法仅适用于零负载下PES和τ的计算，不适用于任意负载(Fz).而宽Fz范围内摩擦性能的计算更能体现实际情况，更有利于解释试验现象.另外，通过建立量子尺度摩擦性能与负载间的关系，更有助于理解量子尺度摩擦的物理本质.

目前，特定负载下固体界面摩擦性能的DFT计算尚未实现自动化和高通量，计算模型构建以及数据后处理浪费了科研人员的大量时间.通常要完整计算1个固体界面体系的摩擦性能，首先需要建立约500～1 000个计算模型，然后准备DFT计算软件所需的输入文件，提交计算任务，计算结束后手动搜索每个构型的总能，拟合能量与界面距离的关系，然后才能获得PES，最后在PES上寻找能量最低的滑动路径，计算摩擦力以及摩擦系数.整个过程人工操作耗费的时间约60小时.另外，科研人员多研究1个体系，耗费的时间就增加1倍.因此，非常有必要提出1个能够实现任意负载固体界面摩擦学性能高通量DFT计算方法.

鉴于此，本文作者提出了1个能够实现自动化建模、计算任务自动提交管理和智能化数据后处理的方法，即自动提取计算结果、拟合数据、绘制势能面、搜索最优滑动路径、输出摩擦力和摩擦系数的固体界面摩擦性能高通量DFT计算方法，该方法能够极大地节约科研人员研究固体界面摩擦性能所需的时间.

1 固体界面摩擦性能的计算方案

1.1 自动化计算流程

固体界面摩擦性能整体设计流程如图1所示，具体如下：(1)读取界面结构文件；(2)分析界面对称性，在x、y和z方向上移动界面构建计算摩擦性能所需的所有位置文件，命名为POSCAR-i-j-k(i、j和k是界面在x、y和z方向上移动的步数).根据界面结构文件构建POTCAR、KPOINTS以及INCAR文件，新建文件夹i-j-k，将对应的POSCAR-i-j-k以及VASP计算所需的其他文件复制到该文件夹；(3)依次进入i-j-k文件夹并调用VASP执行总能计算；(4)依次进入i-j-k文件夹，提取所有计算构型的总能，存入Energy[i][j][k]三维数组.对每组(i,j)，拟合总能与界面距离z的关系E(z).采用最小二乘法拟合总能与界面距离关系E(z).E(z)的函数形式采用12阶多项式，如式(1)所示：

Fig.1 The operation process of the solid interface tribological properties图1 固体界面摩擦学性能计算流程

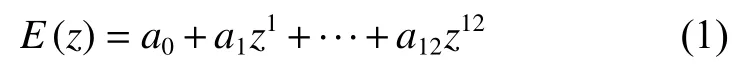
(5)求解不同负载Fz对 应的能量，绘制Fz对应的PES；(6)搜索PES中能垒最低的滑动路径，计算相应的摩擦力f和摩擦系数μ.

1.2 固体界面摩擦性能高通量设计方案

对于固体界面摩擦性能第一性原理计算，计算量的大小取决于界面沿着x，y和z方向平移后，产生的计算模型数量，通常来说这个数量在1 000左右，逐个计算这些模型的能量非常耗时，因此，有必要通过高通量的方法并行-并发计算这些构型的能量.本文中使用图2所示的设计思路实现固体界面摩擦性能的高通量计算.首先基于界面结构生成计算摩擦性能所需的约1 000个计算模型，然后通过调用服务器的作业调度系统，同时将这些计算任务提交到服务器，实现计算任务的并发处理，并调用Vienna Ab initio Simulation Package(VASP)软件，对同一任务使用多核并行计算，实现1个固体界面体系摩擦性能的并发并行计算.

1.3 第一性原理计算方法

本文中第一性原理的总能计算利用基于DFT[18]的Vienna Ab-initio Simulation Package (VASP)软件包[19-21].电子与离子实之间的相互作用采用赝势方法处理.赝势使用投影缀加平面波(PAW)方法[22]，电子之间的交互关联势使用广义梯度近似(GGA)中的Perdew-Burke-Ernzerhof (PBE)[23]泛函.该高通量计算方法中，范德华相互作用被设置为可选变量，需要在程序输入文件中指定.对于文中石墨烯/石墨烯滑动界面的计算，修正格林函数用于修正范德华力(vdW)色散相互作用[24].该高通量计算方法会通过总能收敛性测试确定平面波展开的截断能量，收敛性测试表中是能量差小于1 meV/atom.电子步的能量收敛标准是1×10-6eV.布里渊区使用Monknorst-Pack的K点网格(k-mesh)，程序会通过总能收敛性测试确定K点大小.在总能计算过程中，不弛豫原子的位置，所有体系都使用周期性边界条件.

1.4 摩擦性能的计算方法

首先计算固体界面滑动系统的势能面PES，Zhong等[25]提出的固体界面摩擦过程中的势能V定义如下：

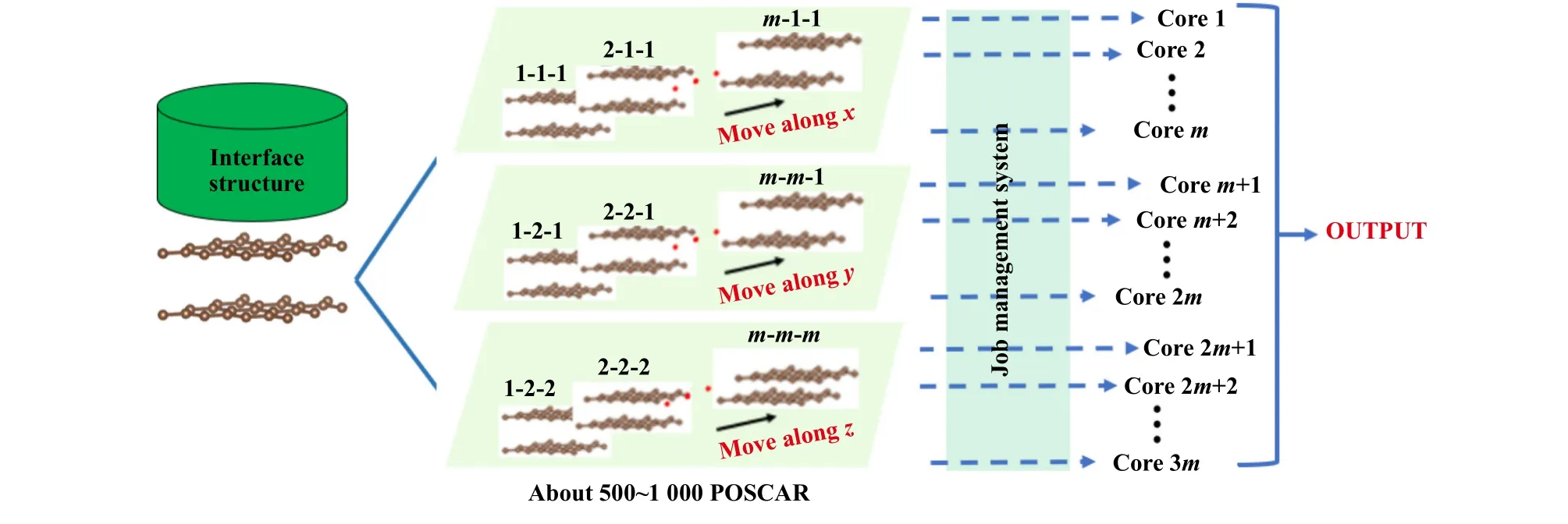
Fig.2 The high throughput algorithm of the solid interface tribological properties图2 固体界面摩擦学性能高通量设计方案

其中Ead是界面能，x和y是界面在这两个方向上移动的距离，z是界面距离，Fz是垂直界面方向的负载，V0是PES中最低的势能，定义为

其中x0和y0是能量最低的界面在x和y方向上移动的距离.界面能Ead的定义如下：

其中EInterface是界面体系的能量，Eup和Edown分别是界面上部分和下部分的能量.负载Fz与吸附能Ead之间的关系满足下面的方程：

其中A是界面面积，本文中A定义为界面的表观接触面积.摩擦力f定义如下：

其中 ΔV是PES势能面滑动路径上鞍点能量与最低点能量之间的差值，d是鞍点与最低点的距离.根据方程(7)，本文中将摩擦力转化为界面剪切强度τ：

摩擦系数 μ定义为

1.5 等负载摩擦计算的实现方法

尽管VASP软件可以计算不同应力下体系总能，但是对于界面体系摩擦性能的计算，这种方法存在两方面的局限.其一，摩擦性能计算需要仅在垂直于界面的方向施加载荷，但是VASP只能在3个方向上同时施加相同的载荷；其二，考虑到周期性边界条件的使用，界面体系需要包含真空层，而VASP软件无法直接对包含真空层的体系施加载荷.因此，该高通量计算方法没有使用VASP直接施加载荷，而是通过Zhong等[23]给出的数值拟合的方法计算等载荷下的摩擦性能.具体实现流程如下：(a)计算不同滑移路径和界面距离对应的体系总能.然后对每条滑移路径上的每个位移点，执行b～e步骤；(b)通过方程(1)拟合界面总能与界面距离之间的关系；(c)使用方程(5)计算负载与界面距离之间的定量关系；(d)通过方程(5)计算给定负载对应的界面距离，根据这个界面距离，使用方程(1)计算给定负载对应的界面总能；(e)通过方程(2)计算给定负载体系的势能；(f)根据给定负载对应的滑动过程中所有体系的势能绘制等负载的PES，根据这个PES计算给定负载下的界面剪切强度和摩擦系数.

2 结果与讨论

本文中以石墨烯/石墨烯滑动体系为例，测试了提出的固体界面摩擦学性能高通量第一性原理计算方法的可靠性.界面在x、y和z方向上分别移动的步数为12、12和30，考虑到界面结构的对称性，总共构建了1 080个计算模型.x和y方向每步移动的距离约为0.21 Å，在z方向每步移动的距离为0.10 Å.这些模型中包含石墨烯/石墨烯滑移体系全部高对称位置，包括TOP(T)位置、Bridge(B)位置、Hollow(H)位置以及Saddle(S)位置，如图3所示.在1 024核服务器上运行该计算软件，每个计算任务使用4个核，服务器同时并行运算256个计算任务.

2.1 能量与界面距离关系

计算完成后，提取了所有体系的总能.图4给出了石墨烯/石墨烯滑动体系高对称位置的能量与界面距离z之间的关系.显然，随着z增大，体系总能降低，当z约为界面间的平衡距离时，界面能降到最低，之后体系总能随着z增大而增大.值得注意的是，总能最低时，不同位置对应的界面距离存在小差异，Top位置对应的z约 为3.45 Å，其他3个位置对应的z约为3.30 Å，如图4所示.另外，当界面距离z约为1.63 Å时，4个高对称位置对应的体系总能近似相等，如图4所示.说明z为1.63 Å时，界面滑动需克服的能垒约为零，从而可能实现超滑.

Fig.3 The high-symmetry Top (T), Bridge (B), Hollow (H) and Saddle (S) sites in the Graphene/Graphene sliding system图3 石墨烯/石墨烯滑动体系的高对称位置

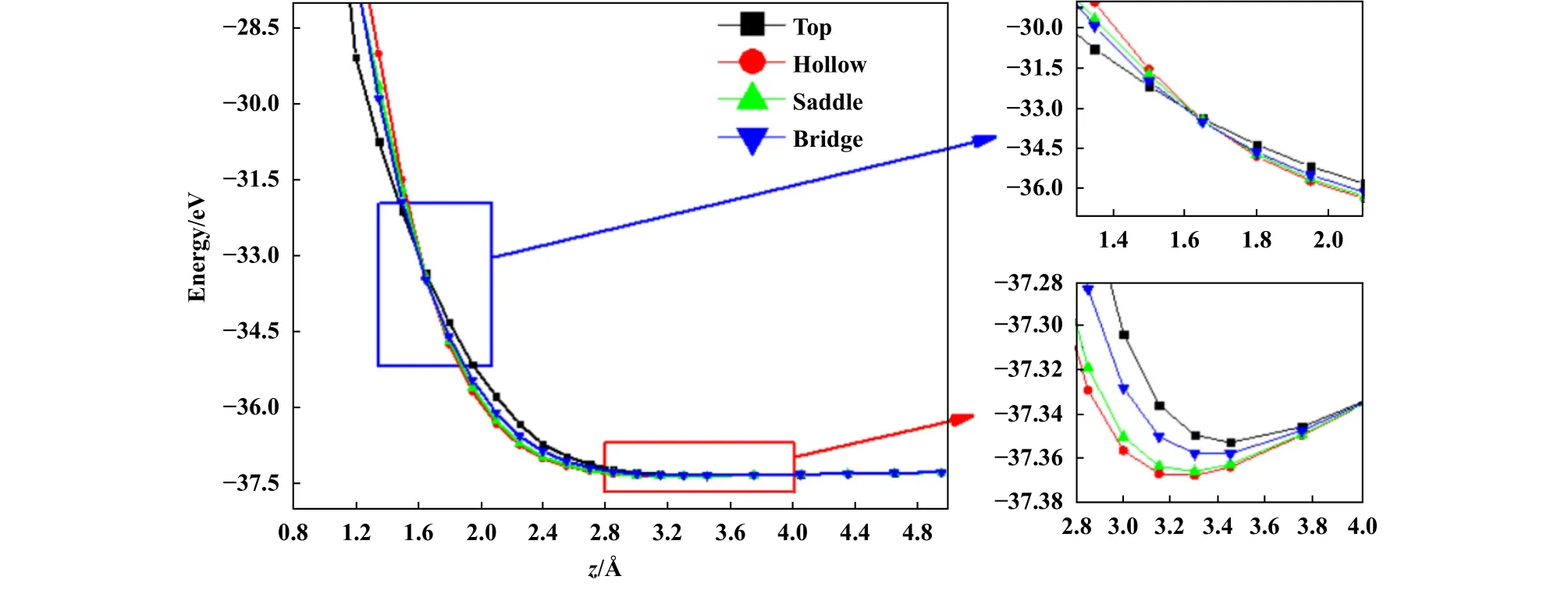
Fig.4 The system energy as a function of interplanar distance z for high-symmetry sites in graphene/graphene system图4 石墨烯/石墨烯滑动体系高对称位置的能量与界面距离z之间的关系

2.2 能量与界面距离关系拟合

之后，拟合了体系能量E与界面距离z之间的关系E(z).E(z)关系的拟合精度决定了给定负载Fz求解能量的准确度，从而决定了摩擦力f和摩擦系数μ的误差.因此，E(z)关系需要非常高的拟合精度，为了提高E(z)关系拟合精度，对z方向30个数据点进行分组，每组包含8个数据点，最后1组数据包含6个数据点，然后采用最小二乘法对每组数据进行拟合.E(z)的函数形式采用12阶多项式，如式(1)所示.最后，检查所有拟合数据，结果表明，采用这种方法拟合的数据绝对误差小于1.0×10-5eV.图5(a)给出了其中1组数据和拟合曲线，图5(b)给出了数据拟合误差.

2.3 势能面PES

图6示出了不同负载对应的势能面(PES)文件，如图6(a)所示，0 GPa条件下，PES比较平坦，T位置势能最高，H位置势能最低，界面沿着H-S-H滑动.随着负载增大，PES起伏逐渐变大，界面滑动需克服的能垒也逐渐增大.当负载约为180 GPa时，PES起伏最大，滑动能垒也达到最大，如图6(c)所示.之后随着负载进一步增大，PES起伏开始变小，滑动能垒也开始变小，当负载约为253 GPa时，PES变得平坦，此时界面滑移能垒与0 GPa时近似相等.随着负载进一步增大，PES起伏又逐渐变大，但此时能量最低的位置变为T位置，H位置转变为能量最高的点，即出现了PES反转.本文中得出的PES随着负载的变化趋势与课题组通过传统的方法计算的结果一致[6]，这验证了该方法的可靠性.

2.4 界面剪切强度和摩擦系数

图7示出了计算的石墨烯/石墨烯滑动体系的界面剪切强度 τ、摩擦系数 μ与负载Fz之间的关系.可以看出，随着Fz的 增大，τ先增大然后减小，最后增大.当Fz为 0 GPa时，τ最小，约0.1 GPa.当Fz约为180 GPa时，τ达到极大值，约3.9 GPa.当Fz约 为253 GPa时，τ降到极小值，约为0.3 GPa，出现了压力诱导超滑现象.这个结果与PES随着负载的变化结果一致.也与课题组通过传统的方法计算的定性结果[6]一致，但在定量比较时出现了偏差.传统方法给出负载约300 GPa时出现了压力诱导超滑现象[6]，但本文中计算的压力诱导超滑的负载值约为253 GPa，这主要是因为计算方法的不同.文献[6]中使用了等界面距离的计算方法，而本文中使用了等负载的计算方法.本文中使用的等负载方法的计算结果更有利于与试验进行直接对比，摩擦系数 μ随着负载的变化曲线也观察到了压力诱导超滑现象，如图7(b)所示.当负载为50～200 GPa时， μ约为0.02～0.03，这与试验值约1 0-2一致[26].

Fig.5 (a) The relationship between energies of system and interface-distances (the black blocks are the calculating energies and the blue line is the fitting curve) and (b) errors between calculating energies and fitting energies图5 (a)体系能量E与界面距离z的关系(黑色方块表示计算数据，蓝色实线表示拟合曲线)；(b)计算和拟合数据之间的误差

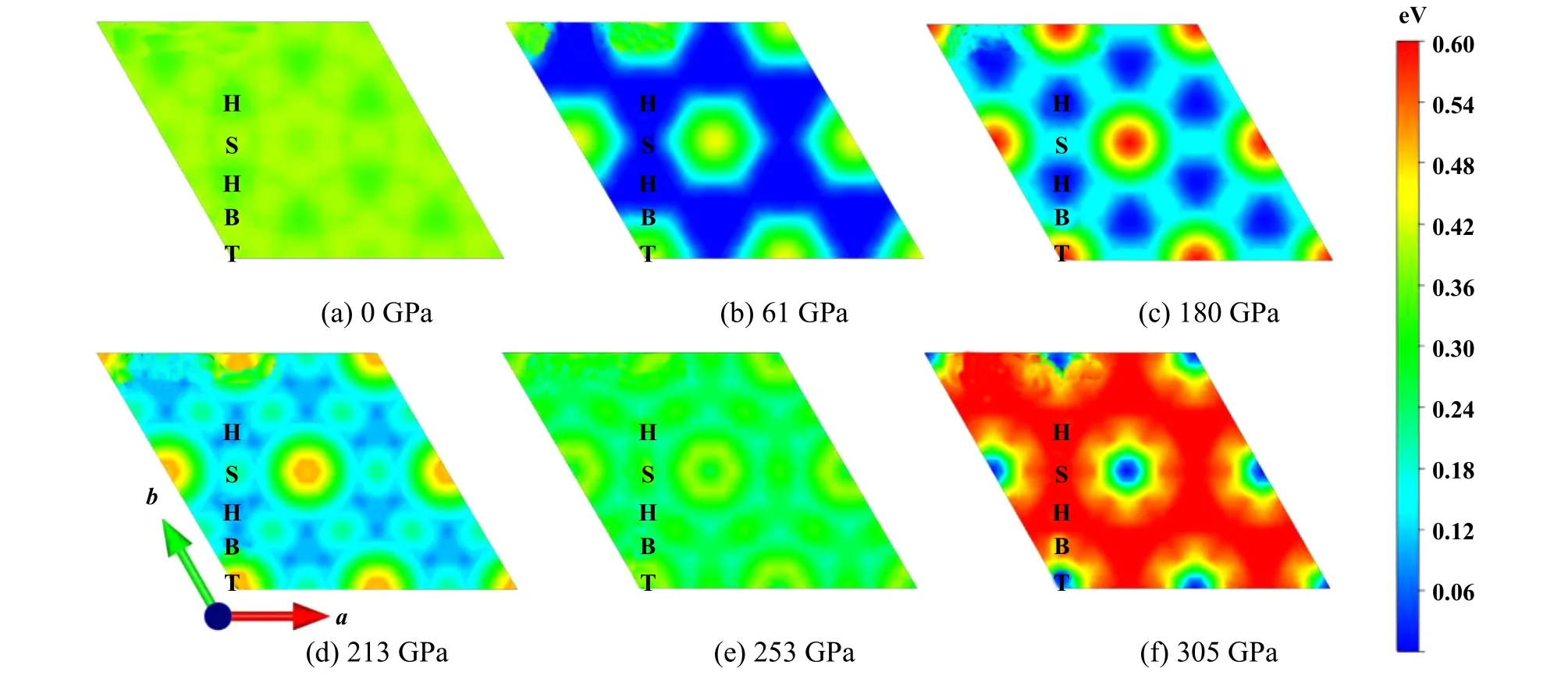
Fig.6 The potential energy surface corresponding to different loads in the graphene/graphene sliding system图6 石墨烯/石墨烯滑动体系中不同负载对应的势能面

2.5 该方法的局限性

尽管该高通量计算方法实现了固体界面摩擦学性能计算的自动化以及高通量计算，并使用石墨烯/石墨烯滑动体系验证了该方法的可靠性，但该方法仍然存在一些局限性.首先，由于DFT计算本身无法直接引入温度，因此该方法也没有考虑温度对摩擦性能的影响；其次，该方法不仅能够计算范德华相互作用结合的简单二维材料，也可以计算氧化物和金属之间的同/异质界面，但需要注意的是，该方法没有考虑摩擦过程中界面之间原子的交换以及界面摩擦化学反应.摩擦过程中非晶以及较粗糙的界面可能更容易发生界面原子的转移，因此，使用该方法计算非晶或者较粗糙的界面时，需要仔细考虑计算模型以及结果的合理性；另外，该方法没有考虑气氛环境的影响，气氛环境对固体界面摩擦的影响普遍存在，因此，非常有必要在该方法中引入气氛环境的影响，这也是该方法下一步需要改进的方向.

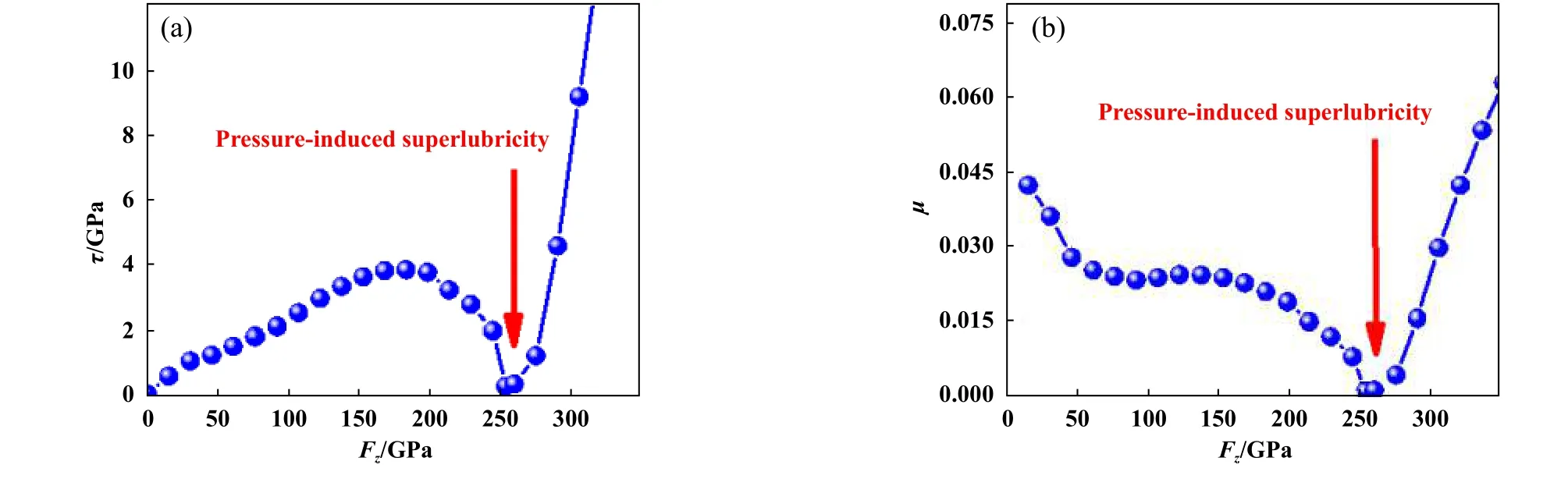
Fig.7 (a) Interfacial shear strength τ and (b) friction coefficient μ as a function of the load Fz in the graphene/graphene sliding system图7 石墨烯/石墨烯滑动体系中(a)界面剪切强度τ和(b)摩擦系数μ与负载Fz之间的的关系

3 结论

报道了1个基于第一性原理的固体界面摩擦学性能高通量计算方法，并以石墨烯/石墨烯滑动体系为例验证了该方法的可靠性.主要结论如下：

a.该方法实现了固体界面摩擦学性能计算的自动化，即自动构建计算模型、自动提交管理计算任务和智能分析计算数据，直接输出界面的势能面、摩擦力和摩擦系数，能够极大地节约科研人员使用第一性原理研究固体界面摩擦性能所需的时间.

b.该方法实现了固体界面摩擦性能计算的高通量，即1 000多个计算任务的并发并行计算，提高了固体界面摩擦性能的计算效率.

c.使用该方法计算的石墨烯/石墨烯滑动体系的势能面与使用传统方法的计算结果一致，摩擦系数与试验结果符合，从而验证了该方法的可靠性.