条带开采中采厚对地表沉陷影响的数值模拟研究

张彩凤

（安徽水利水电职业技术学院 本科教育工作部，安徽 合肥 231603）

国家有关统计资料表明，2021年全国能源消耗总量为52.4亿吨，其中煤炭能耗占总能耗的66.8%，同比增长5.2%［1］。但伴随着几十年来的粗放式无序开采，我国正面临着煤炭资源枯竭的局面，而以煤炭为主体的能源消费结构在短期内不会改变，浅部煤炭资源逐步减少，煤炭生产向深部延伸，开采强度、开采范围的不断扩大，使得建筑物下、铁路下和水体下（下文简称“三下”）采煤所占比重越来越多。据统计，“三下”压煤总量已达179亿多吨，其中67%为建筑压煤。而建筑物下采煤会造成开采区地表沉陷面积的不断扩大，由于煤层赋存条件复杂，受构造应力、地下水作用等因素制约，采空区容易出现冒落或塌陷现象，严重时会威胁到人们的生命财产安全。因此，对采动破坏规律和减小采动破坏影响的研究成为首先需要解决的问题。在此背景下，条带开采作为一种新型的开采方式应运而生，并得到了广泛的应用。目前国内已经开始应用这种新型的采煤方法，但对其理论与实践尚处于探索阶段。条带开采能够有效地控制上覆岩层下沉和地表移动变形，保护地面建筑物和生态环境，是减少采动破坏影响的重要采煤方式，同时也是煤矿“绿色开采技术”体系中最主要的措施［2］，因此对它的研究具有重要意义。

1 研究基础

国内关于条带开采已开展了大量的研究工作，主要集中在条带开采煤柱的稳定性、提高采出率的方法以及开采尺寸设计等方面。邓喀中等［3］对多煤层条带开采煤柱稳定性进行了研究；赵柯［4］总结了不同采出率条件下条带开采地表的移动变形规律；张纪堂等［5］对深井条带开采中留设条带长期稳定性进行了系统分析；刘承旭等［6］对条采工况推进过程中的地表沉陷规律进行了研究，并解算出地表各项移动参数；胡炳南［7］从力学分析出发，导出了条带开采沉陷的解析解，分析了条带开采沉陷主控因素对开采沉陷的影响；赵扬锋等［8］-［9］采用ANSYS对水平煤层条带开采进行了二维有限元数值模拟研究，分析了条带开采中采出率以及条带开采中上覆岩层的岩性的变化对地表沉陷的影响规律；杜子龙等［10］基于FLAC3D对某深部矿井条带开采工作面数值模拟分别模拟研究了两个工作面开采对地表下沉的影响；王征世［11］应用FLAC3d对矿井深部宽条带开采进行分析研究，主要阐述了深部条带开采沉陷的数学模型选取。但条带开采采厚与地表下沉系数关系的研究还不够充分。采厚是条带开采的一项重要参数，对上覆岩层及地表的移动过程起着重要影响作用。采厚越大地表移动变形值越大，但采厚过小影响生产效率，不能实现条带开采高产高效的特点。因此，研究条带开采地表沉陷随采厚变化的规律具有理论意义。本文采用ANSYS数值模拟方法，研究开采厚度与地表移动的关系，以期揭示影响规律。

2 计算几何模型

本文针对条带开采的实际情况，建立了条带开采有限元二维计算模型，如图1所示。煤层为水平煤层，开采深度580 m，煤层厚度3 m，地表走向模拟1000 m，开采宽度90 m，留宽60 m。在采动过程中，为了消除边界效应的影响，真实地展示地表沉陷的实际状况，采用平面应变模型计算煤柱两侧各预留200 m煤柱。模拟岩层由表及下依次是：表土层、粉砂岩、细砂岩、砾岩、砂岩、砂质页岩、煤、砂质页岩。根据现场实测资料及理论分析，可知软的顶板岩层、软的主采煤层和软的煤层底板岩层（简称“三软”）厚松散层条件下条带工作面顶板垮落具有明显的分段特征，并且可确定出各岩层力学参数和边界条件。各岩层的物理力学参数见表1，模型取煤层倾向方向为x轴，重力方向为y轴，模型仅受重力的作用。模型边界条件的设置如下：（1）模型左右两边的边界为单向约束，即边界水平位移为零；（2）模型底部边界为双向约束固定，即底部边界为水平，垂直位移为零；（3）模型顶部为自由边界。本文从岩层内物质的力学特征出发，为了计算方便，将岩石和煤都视为各向同性的弹塑性材料并应用理想弹塑性模型。采用莫尔-库伦准则，建立了煤与岩层的材料本构关系。在开采过程中应用定采留比条带状开采方法，并利用ANSYS有限元程序进行数值模拟分析。

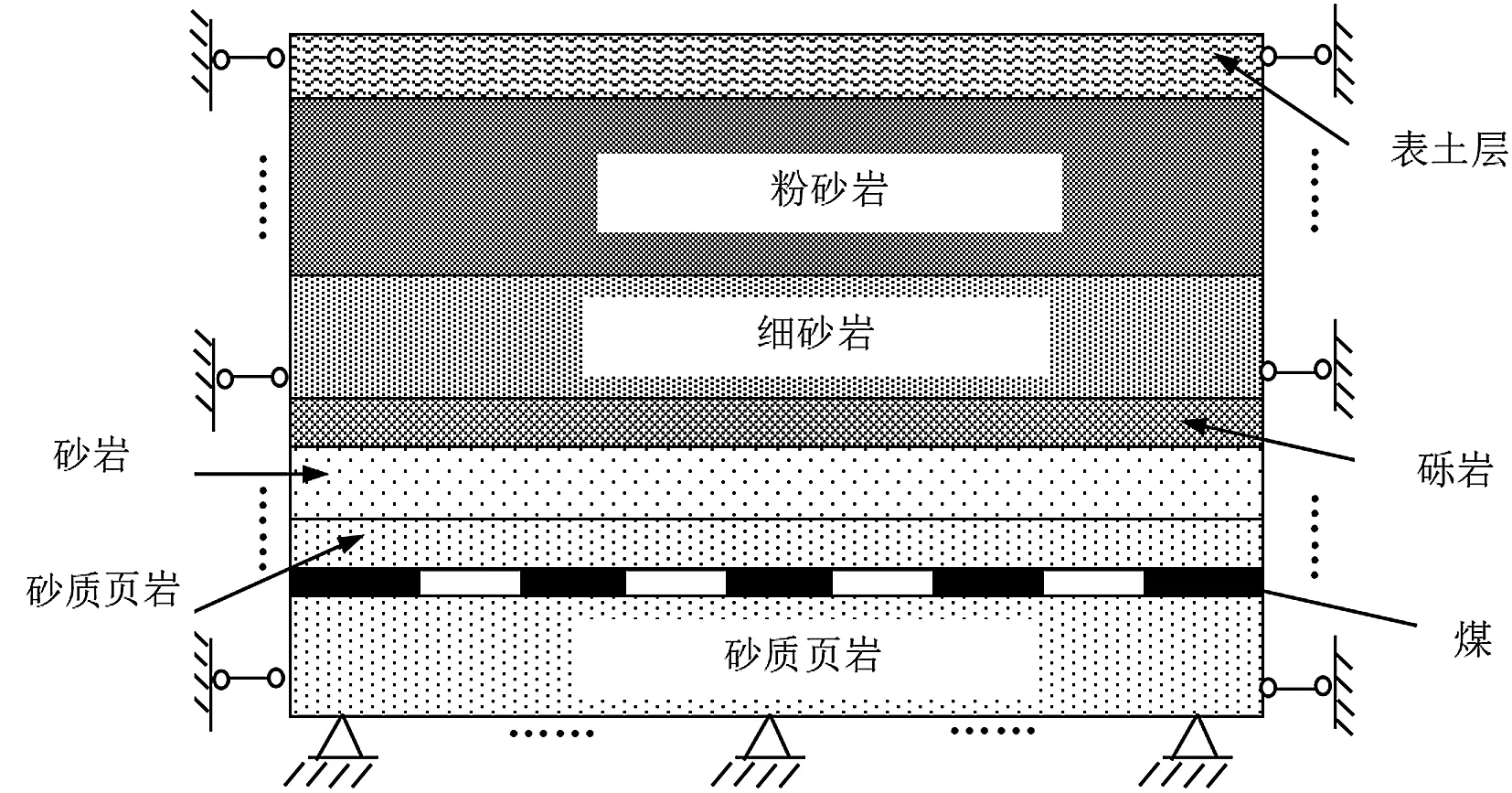
图1 二维计算模型

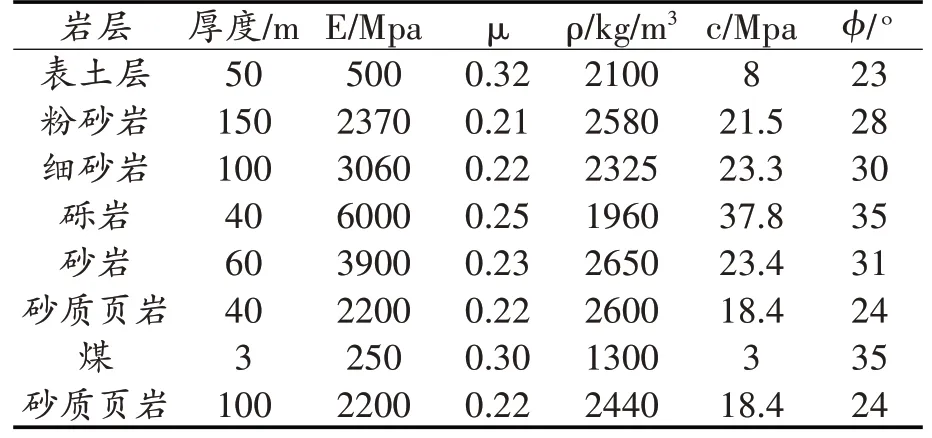
表1 各岩层参数

3 模拟方案及结果

为了模拟不同采厚对条带开采地表沉陷的影响规律，采厚分别取1 m、2 m、3 m、5 m、8 m，开采时条带开采的采出率设为60%，为使各采厚下的模拟结果具有可比性，各模拟方案的边界条件、岩层参数等条件均相同，从而建立5个数值模拟模型。5个数值模拟模型是采厚为1 m、2 m、3 m、5 m、8 m的数值模拟模型。

图2 到图7中，A为采厚为1 m时位移曲线，B为采厚为2 m时位移曲线，C为采厚为3 m时位移曲线，D为采厚为5 m时位移曲线，E为采厚为8 m时位移曲线。图8、图9则是采厚为2 m和5 m时y方向应力云图。通过对上述各方案进行模拟计算，得到不同采厚条件下地表最大下沉值量与最大拉压应力值，具体如表2所示。采厚与最大下沉量和水平位移以及下沉系数的关系如图10所示，采厚与最大拉压应力关系如图11所示。（注：图中SMN为应力最小值，本文中就是最大压应力；SMX为应力最大值，本文中就是最大拉应力；DMX为最大位移。）

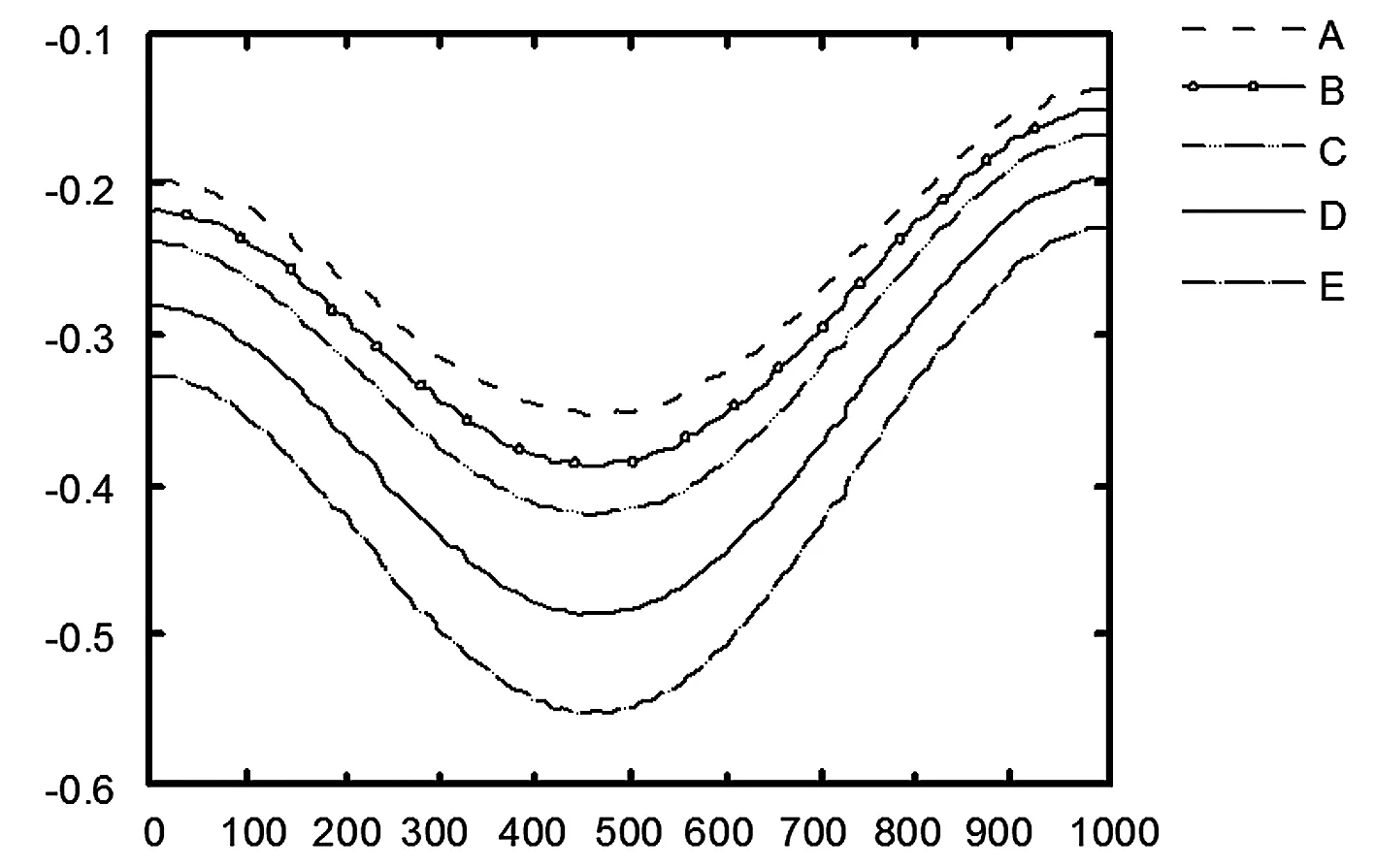
图2 不同采厚时地表下沉曲线

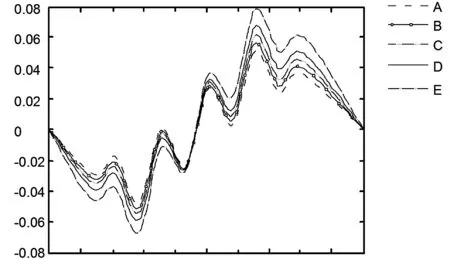
图7 不同采厚时顶板的水平位移曲线

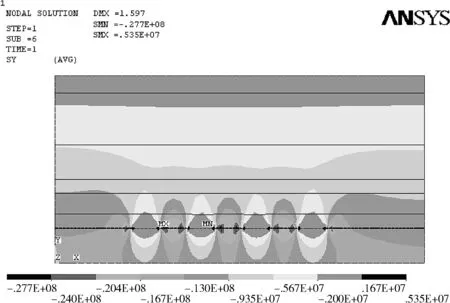
图8 采厚为2 m时y方向应力云图

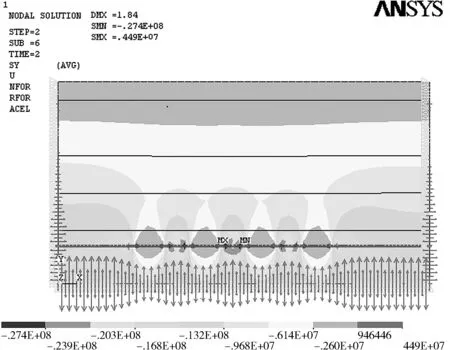
图9 采厚为5 m时y方向应力云图

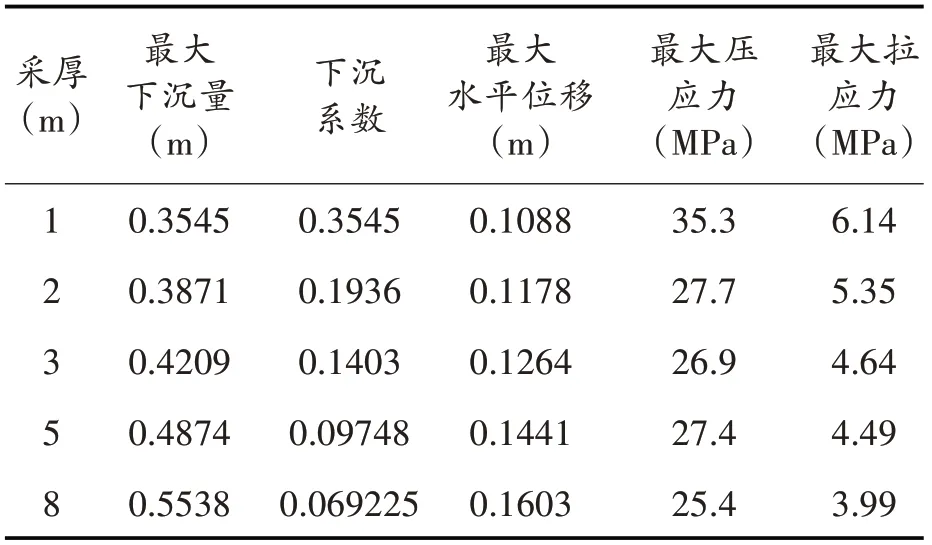
表2 不同采厚时地表最大下沉量与最大拉压应力值表

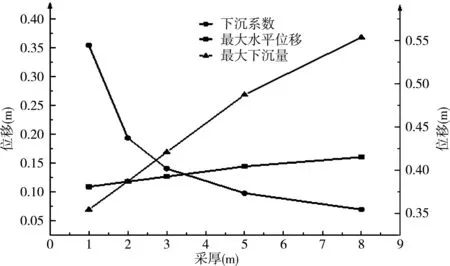
图10 采厚与最大下沉量、水平位移和下沉系数关系图

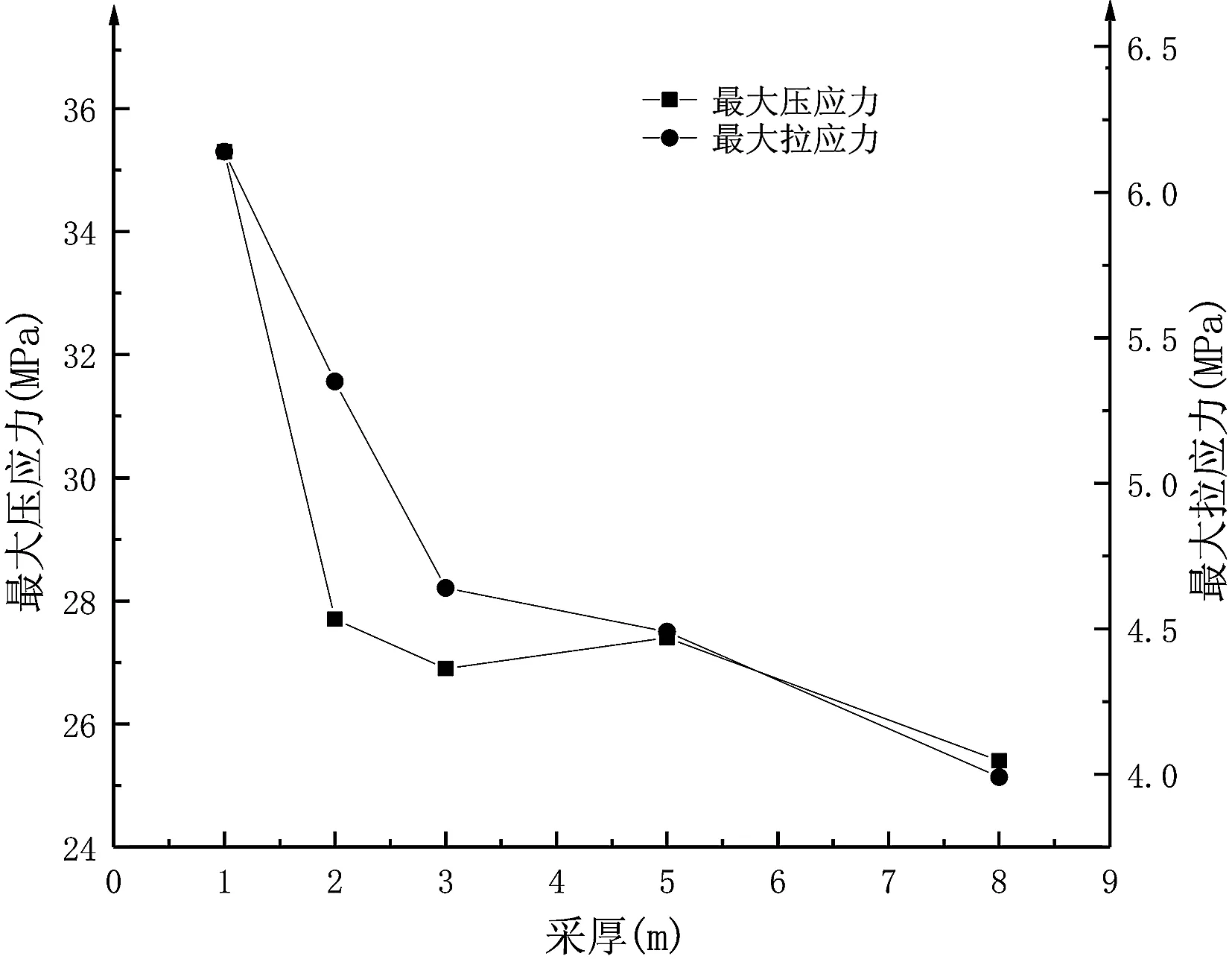
图11 采厚与最大拉压应力关系图

4 模拟结果分析

（1）从图2、图3可以看出，随着条带开采厚度的增加，地表下沉曲线越来越陡，曲线呈现下凹趋势，即增幅逐渐增大，下沉量也逐渐增大。不同采厚情况下的地表下沉曲线变化趋势相似，最大下沉点均出现在开采范围的中心点处，且随着条带开采厚度的增加，地表水平位移值呈非线性增加，最大值分别出现在曲线的250 m和750 m处，地表水平移动的极值点位于采空区上方，且开采厚度的增加对极值点位置影响较小，开采中心位置处不同采厚的水平位移曲线差异不显著。

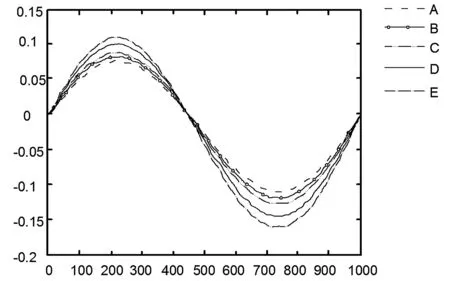
图3 不同采厚时地表水平位移曲线

（2）从图4、图5可以看出不同采厚下顶板上一岩层水平移动下沉的变化规律，随着条带开采厚度的增加，顶板上一岩层下沉量逐渐增大。相较地表下沉，图2最大下沉点位于开采范围中心位置处，顶板上一岩层在开采中心位置处的下沉量虽是最大值但变化较为平缓，致使最大下沉位置的范围较地表下沉更大；顶板上一岩层的水平位移随着条带开采厚度的增加而增大，但煤柱处采厚为5 m的水平位移值激增大于采厚为8 m的水平位移值，且开采中心位置处不同采厚的水平位移曲线几乎重合。顶板上一岩层水平位移曲线波动程度与波动幅值呈正比，与幅值变化的开采位置范围大小成反比，水平位移采空区并非煤柱一侧，且开采厚度的增加对极值点位置影响较小。值呈非线性的增大最大值分别位于曲线的275 m和650 m处，最值点同样位于该处。

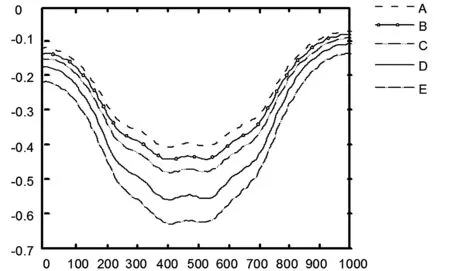
图4 不同采厚时顶板上一岩层下沉曲线

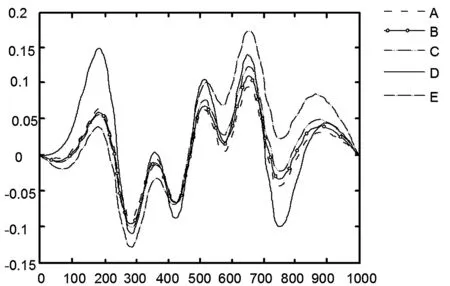
图5 不同采厚时顶板上一岩层水平位移曲线

（3）从图6、图7可以看出不同采厚条件下顶板的水平移动下沉规律，随着条带开采厚度的增加，顶板的下沉量逐渐增大。相同采厚值下顶板下沉曲线较地表下沉曲线相比极值增多并且波动起伏明显，如果采厚过大，波浪下沉波及到地表。上覆岩层波状下沉高度不仅与开采条带的宽度相关，而且与留设煤柱宽度有关。最大下沉点依旧位于开采范围中心位置处；顶板的水平位移是对称的，随着条带开采厚度的增加而增大，最大水平位移分别位于曲线的275 m和650 m处，同样，同一采厚值的顶板水平位移曲线较地表水平位移曲线极值增多波动明显，但总体趋势一致。

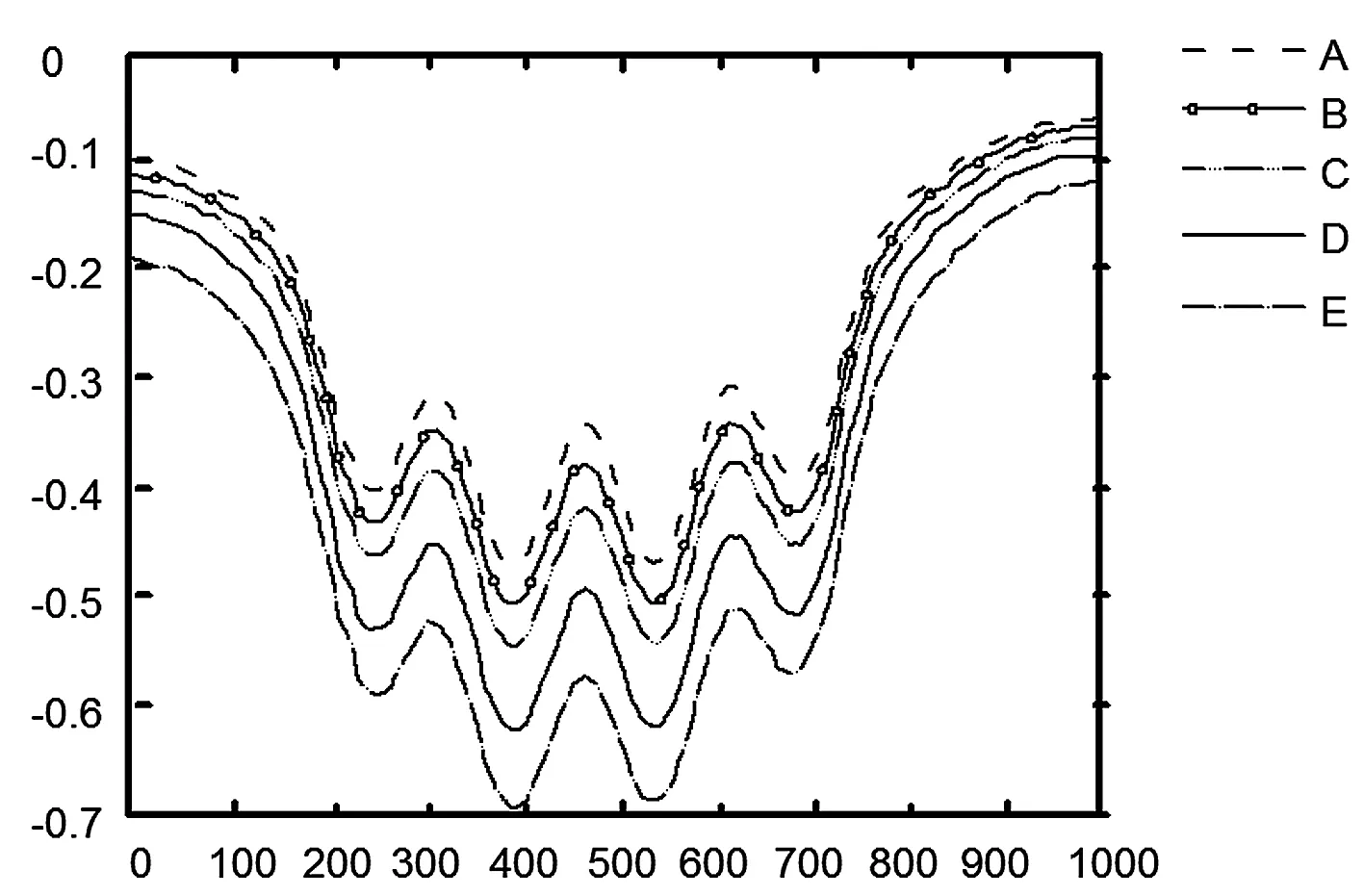
图6 不同采厚时顶板下沉曲线

（4）从图8、图9可以看出最大压应力在所留煤柱的位置，最大拉应力发布在采空区的上方，在煤柱体两侧形成了一个应力集中区，远大于煤柱体的平均应力，煤柱实际承受的载荷主要与地层厚度和开采尺寸有关，且随着采厚的增加，支承压力的分布范围明显增大，平均应力值明显增大。如果条带煤柱宽度不大，煤柱可能最终被压垮，导致地表沉降加剧，不能起到条带开采的效果，如果条带煤柱过宽，地表将再次形成波浪下沉盆地，顶板抗压强度逐渐减小，而围岩则不断向中间发展，最终造成破坏严重，不利于建筑物的保护。

（5）从图10可以看出，随着采厚的增大，最大下沉量、最大水平位移呈线性增大但增幅较小。但下沉系数线性减小且在采厚较小时，下沉系数下降较快，当采厚大于2 m时下沉系数下降逐渐平缓，即随着开采厚度的增加，采厚对下沉系数的影响较小。

（6）从图11可以看出，随着采厚的增大，最大拉压应力均减小，当采厚大于2 m时，最大压应力逐渐变化平缓趋于常数，而最大拉应力呈线性减小。

5 结论

（1）对水平煤层的开采引起的地表变形位移情况进行数值模拟研究发现：地面塌陷变形缓慢，地表最大下沉位移和最大水平位移呈对称性分布；在其它因素保持不变的条件下，随着开采厚度的增加，地表最大沉降值略有增大的趋势，且地表沉降值和水平移动值逐渐增大，即地表沉降产生的盆地面积逐渐增大，对地表变形的影响程度必然有所增加；不同采厚回采期间，煤层顶板一定范围内的岩层下沉曲线均具有明显的分区特征，煤层顶板岩层水平位移曲线均具有明显的波动特征。因此，在采煤时选择适当采厚，以防止地表出现过大的下沉与水平移动，为“三下”压煤开采以及地面建筑工程的建设提供合理的参考依据。

（2）在条带开采时，当采厚较大时，虽然下沉系数较小，但是地表的最大下沉量却较大，为了保护地面建筑，应减小开采率；当采厚较小时，虽然最大下沉量小，但下沉系数较大，最大拉压应力都较大，应增大留宽，随着煤柱留设的宽度的增大，通过合理的煤柱错距布置，可以减缓地表下沉的波动幅度，减轻地表变形以及煤柱体两侧的应力集中，以免煤柱破坏。当建筑物临界变形满足要求时，可在不增加地表沉降值或增加地表沉降值的前提下，适当增加建筑物开采厚度，使建筑物下采煤效益最大化。