闭元确定的拓扑系统中闭包元及其应用

高 雅，吴洪博

（陕西师范大学数学与统计学院，陕西西安 710062）

1 引言

根据研究方法的不同，拓扑理论的研究分为两大学派：有点化学派和无点化学派［1～5］.王国俊教授在序结构基础上建立的模糊拓扑学和拓扑分子格理论是将两者融合的代表［6～8］.文献［9～12］结合一般拓扑学的研究方法对Locale 理论的连通性质等进行了研究.1989年，Steven Vickers 将Locale 理论与一般拓扑理论结合为一体，在文献［13］中引进的一种新型的拓扑学研究对象：拓扑系统，并从格序理论方面对拓扑系统的性质和应用进行了讨论.目前，我国学者主要从点集拓扑理论方面对拓扑系统的性质及相关问题进行研究，并且取得了一些相关成果［14～24］.

从目前的研究结果看，拓扑系统中的闭集是通过拓扑系统空间化形式中的开集取补定义的［16～19］，因此其结果适用于空间式拓扑系统，但未必适用于一般的拓扑系统.因此，本文引入了拓扑系统的对偶拓扑系统—闭元确定的拓扑系统，并取得了一些相关的结果.

2 预备知识

定义1［1］设P是集合，“≤”是P上的二元关系.若(P，≤)满足以下条件：

（1）∀a∈P，a≤a.

（2）∀a，b∈P，若a≤b，b≤a，则a=b.

（3）∀a，b，c∈P，若a≤b，b≤c，则a≤c.

则称(P，≤)是偏序集.

定义2［1］余FrameA是一个满足以下条件的偏序集：

（1）∀S⊆finA，S的上确界存在，即∨S存在；

（2）∀S⊆A，S的下确界存在，即∧S存在；

（3）满足第二无限分配律，即，∀a∈A，∀S⊆A，有a∨(∧S)=∧{a∨s：s∈S}.

注1［1］（1）本文中S⊆finA表示S是A中的有限子集；（2）由于余Frame是满足第二无限分配律的完备格，将其中最大元记作1，最小元记作0.

定义3［1］设A，B是余Frame.若映射f：A→B满足以下条件：

（1）∀S⊆finA，f(∨S)=∨f(S);

（2）∀S⊆A，f(∧S)=∧f(S).

则称f：A→B是余Frame同态.

3 由闭元确定的拓扑系统及相关性质

定义4设A是余Frame，X是集合，⊨⊆X×A，将(x，a) ∈⊨记作x⊨a.若∀x∈X

（1）∀S⊆finA，x⊨∨S⇔∃a∈S，x⊨a；

（2）∀S⊆A，x⊨∧S⇔∀a∈S，x⊨a.

则称(X，A，⊨)为闭元确定的拓扑系统，余FrameA中的元素称为拓扑系统中的闭元.

在本文中，将闭元确定的拓扑系统(X，A，⊨)记为D，将X记为PtD，将A记为ΩD.

引理1设D=(PtD，ΩD，⊨)是闭元确定的拓扑系统，1，0分别是ΩD的最大元和最小元.∀a，b∈ΩD，则：

（1）∀x∈PtD，x⊨1；

（2）∀x∈PtD，x| ≠0；

（3）若x⊨a，a≤b，则x⊨b.

证明根据定义4易证.略.

定义5设D=(PtD，ΩD，⊨)是闭元确定的拓扑系统.定义映射ex：ΩD→2PtD如下：∀a∈ΩD

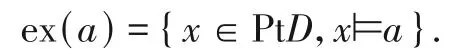
∀a∈ΩD，称ex(a)为a的余范围.

定理1设D=(PtD，ΩD，⊨)是闭元确定的拓扑系统.令Ω(PtD)={ex(a)：a∈ΩD}，则集族Ω(PtD)对有限并运算和任意交运算封闭，并且

（1）ex(0)=∅，ex(1)=PtD；

（2）∀a，b∈ΩD，ex(a) ∪ex(b)=ex(a∨b)；

（3）∀S⊆ΩD，∩{ex(s)：s∈S}=ex(∧S).

证明（1）由引理1可证.略.

（2）∀x∈PtD，结合定义4，定义5，

x∈ex(a) ∪ex(b) ⇔(x∈ex(a)或x∈ex(b)) ⇔

(x⊨a或x⊨b) ⇔x⊨a∨b⇔x∈ex(a∨b).

因此，∀a，b∈ΩD，ex(a) ∪ex(b)=ex(a∨b).

（3）∀x∈PtD，结合定义4，定义5，

x∈∩{ex(s)：s∈S}⇔(∀s∈S，x∈ex(s)) ⇔

(∀s∈S，x⊨s) ⇔x⊨∧S⇔x∈ex(∧S).

因此，∀S⊆ΩD，∩{ex(s)：s∈S}=ex(∧S).

由于ΩD是完备格，因此，a∨b∈ΩD，∧S∈ΩD.结合（1）～（3）可知：集族Ω(PtD)对有限并运算和任意交运算封闭.

引理2在闭元确定的拓扑系统D=(PtD，ΩD，⊨)中，映射ex：ΩD→2PtD是保序映射.

证明由引理1（3）易证.略.

4 闭元确定的拓扑系统中的闭包元及性质

定义6在闭元确定的拓扑系统D=(PtD，ΩD，⊨)中，定义

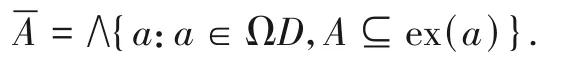
称该映射为拓扑系统D的闭包映射，并称为集合A在拓扑系统D=(PtD，ΩD，⊨)中的闭包元.

定理2在闭元确定的拓扑系统D=(PtD，ΩD，⊨)中，闭包元有如下的性质：

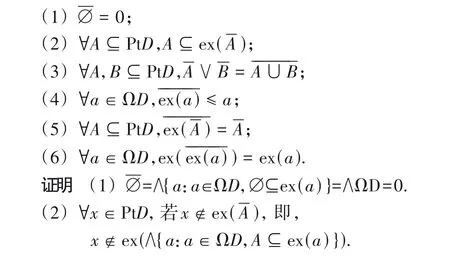
因此，x|≠∧{a：a∈ΩD，A⊆ex(a)}.从而由定义4（2）可知：∃a∈ΩD，使得A⊆ex(a)，且x|≠a.

因此有A⊆ex(a)，且x∉ex(a).因此，x∉A.

综上可知：∀A⊆PtD，A⊆ex().

（3）首先，由于A⊆A∪B，因此，{a：a∈ΩD，A⊆ex(a)}⊇{a：a∈ΩD，A∪B⊆ex(a)}.因此，

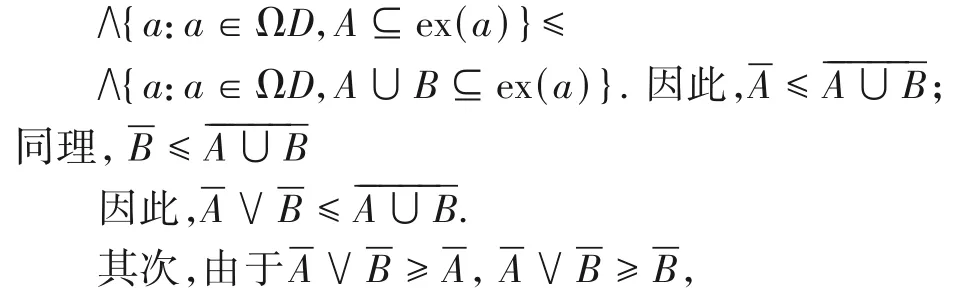
结合引理2和定理2（2）得：

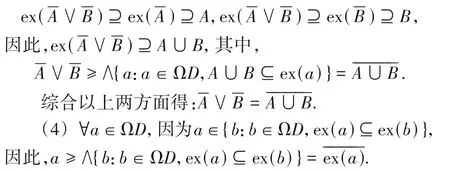
（5）首先，∀A⊆PtD，a∈ΩD.

利用上面这个结论可得：∀A⊆PtD，

注2在闭元确定的拓扑系统D=(PtD，ΩD，⊨)中，关于闭包元有如下的结论：

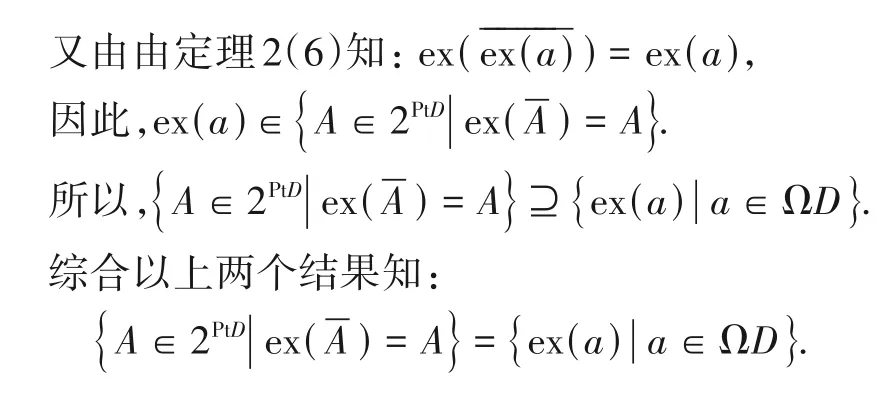
5 Kuratovski闭包定理

定义7(Kuratovski 闭包算子)设X是非空集合，L是余Frame.双映射Ex：L→2X，Cl：2X→L满足条件：

（1）∀a，b∈L，Ex(a∨b)=Ex(a) ∪Ex(b)；

（2）Cl(∅)=0，Ex(0)=∅；

（3）∀A⊆X，A⊆Ex(Cl(A))；

（4）∀A，B⊆X，Cl(A) ∨Cl(B)=Cl(A∪B)；

（5）∀a∈L，Cl(Ex(a)) ≤a.

则称(Ex，Cl)是(X，L)上的Kuratovski闭包算子.

引理3设X是非空集合，L是余Frame，(Ex，Cl)是(X，L)上的Kuratovski闭包算子.则

（1）∀a，b∈L，若a≤b，则Ex(a) ⊆Ex(b)；

（2）∀A，B∈2X，若A⊆B，则Cl(A) ≤Cl(B)；

（3）∀A∈2X，Cl(Ex(Cl(A)))=Cl(A)；

（4）∀a∈L，Ex(Cl(Ex(a)))=Ex(a).

证明（1）结合定义7（1）可证.略.

（2）结合定义7（4）可证.略.

（3）结合定义7（3）可得：Cl(Ex(Cl(A))) ≥Cl(A)；再由定义7（5）得：Cl(Ex(Cl(A))) ≤Cl(A).

综合两不等式得：Cl(Ex(Cl(A)))=Cl(A).

（4）由定义7（3）得：Ex(a) ⊆Ex(Cl(Ex(a)))；

其次，结合定义7（5）得：Ex(a) ⊇Ex(Cl(Ex(a))).

所以，Ex(Cl(Ex(a)))=Ex(a).

引理4设X是非空集合，L是余Frame，(Ex，Cl)是(X，L) 上的Kuratovski 闭包算子.则集族F={A∈2X|Ex(Cl(A))=A}是集合X上相对于某拓扑的闭集族.

证明（1）由定义7（2）得：Ex(Cl(∅))=Ex(0)=∅，因此，∅∈F；再由定义7（3）得：X⊆Ex(Cl(X))，

所以，X=Ex(Cl(X))，根据F定义得：X∈F；

（2）设A，B∈F.则A=Ex(Cl(A))，B=Ex(Cl(B)).

结合定义7（1）、（4）得：

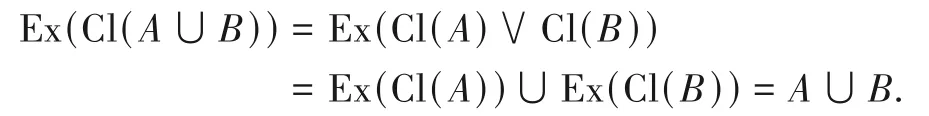
根据F定义得：A∪B∈F；

（3）设{Aj|j∈J}⊆F，则

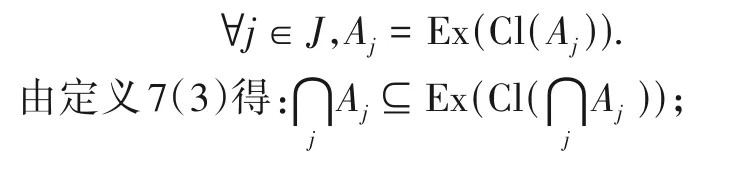
由（1）～（3）知：集族F={A∈2X|Ex(Cl(A))=A}是集合X上相对于某拓扑的闭集族.

引理5设X是非空集合，L是余Frame，(Ex，Cl)是(X，L) 上 的Kuratovski 闭包算子.则Ex：L→2X是 余Frame同态.

证明（1）∀a，b∈L，根据定义7（1）可得：

Ex(a∨b)=Ex(a) ∪Ex(b)；

（2）∀{aj|j∈J}⊆L.

由于∀j∈J，aj≥∧{aj|j∈J}.结合引理3（1）得：∀j∈J，Ex(aj) ⊇Ex(∧{aj|j∈J}).则

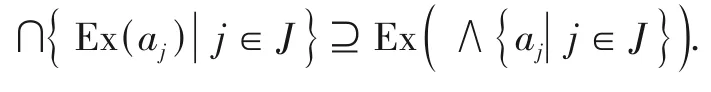
又由于∀j∈J，∩{Ex(aj)|j∈J}⊆Ex(aj).由引理3（2）得：∀j∈J，

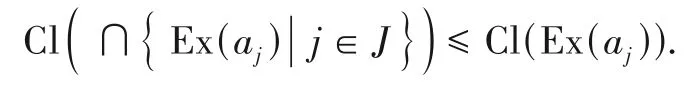
再由定义7（5）得：∀j∈J，Cl(Ex(aj)) ≤aj.

将两者结合得：∀j∈J，Cl(∩{Ex(aj)|j∈J})≤aj.

因此，Cl(∩{Ex(aj)|j∈J}) ≤∧{aj|j∈J}.

结合引理3（1）得：

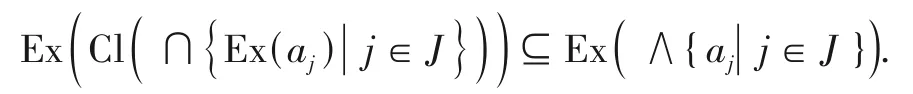
再由定义7（3）得：

∩{Ex(aj)|j∈J}⊆Ex(Cl(∩{Ex(aj)|j∈J}))，因此，∩{Ex(aj)|j∈J}⊆Ex(∧{aj|j∈J}).

结合两式得 ：Ex(∧{aj|j∈J})=∩{Ex(aj)|j∈J}.

根据定义3知Ex：L→2X是余Frame同态.

引理6设X是非空集合，L是余Frame，(Ex，Cl)是(X，L)上的Kuratovski 闭包算子.定义从X到L的二元关系"⊨"如下：∀(x，a) ∈X×L，

则(X，L，⊨)是闭元确定的拓扑系统.

证明由引理5知：Ex：L→2X是余Frame同态.结合"⊨"的定义得：

（1）∀a，b∈L，∀x∈X，

x⊨a∨b，当且仅当x∈Ex(a∨b)，当且仅当x∈Ex(a) ∪Ex(b)，当且仅当x∈Ex(a)或x∈Ex(b)，当且仅当x⊨a或x⊨b；

（2）∀S⊆L，∀x∈X，

x⊨∧S，当且仅当x∈Ex(∧S)，当且仅当x∈∩{Ex(s)：s∈S}，当且仅当∀s∈S，x∈Ex(s)，当且仅当∀s∈S，x⊨s.

根据定义4知：(X，L，⊨)是闭元确定的拓扑系统.

定理5(Kuratovski闭包算子定理)设X是非空集合，L是余Frame，(Ex，Cl)是(X，L)上的Kuratovski 闭包算子.则存在唯一的闭元确定的拓扑系统D=(X，L，⊨)使得在该拓扑系统中

证明设X是非空集合，L是余Frame，(Ex，Cl)是(X，L)上的Kuratovski 闭包算子.定义从X到L的二元关系"⊨"如下：∀(x，a) ∈X×L，

则由引理5 知Ex：L→2X是余Frame 同态，由引理6知D=(X，L，⊨)是闭元确定的拓扑系统.

由定义7（3）知：A⊆Ex(Cl(A))，又Cl(A) ∈L，则Cl(A) ∈{a：a∈L，A⊆Ex(a)}；

又∀a∈L，若A⊆Ex(a)，则结合引理3（2）可得：Cl(A) ≤Cl(Ex(a))；又由定义7（5）得：

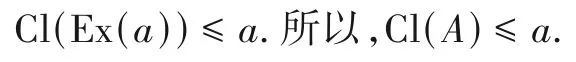
综合两方面知：Cl(A)=∧{a：a∈L，A⊆Ex(a)}.

因此，结合定义6知：在闭元确定的拓扑系统(X，L，⊨)中，

下面证明满足条件的闭元确定的拓扑系统D=(X，L，⊨)的唯一性.

若闭元确定的拓扑系统D1=(X，L，⊨1)也满足因此，在闭元确定的拓扑系统D1=(X，L，⊨1)中，∀a∈L，有

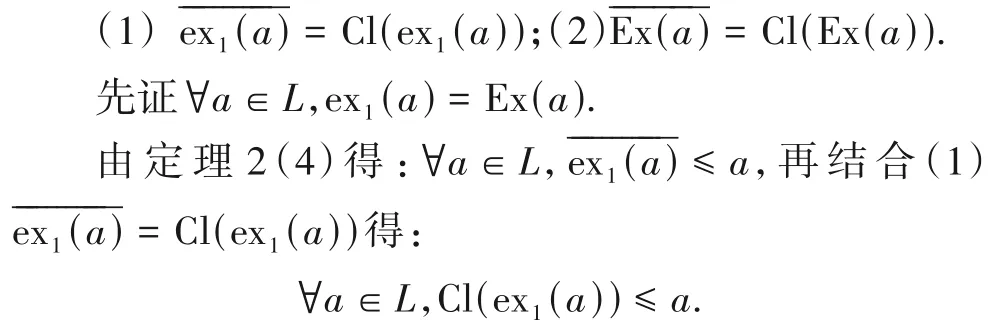
因此，∀a∈L，Ex(Cl(ex1(a))) ⊆Ex(a).

又根据定义7（3）得：ex1(a) ⊆Ex(Cl(ex1(a)))，

所以，∀a∈L，ex1(a) ⊆Ex(a)；

又由定义7（5）得：∀a∈L，Cl(Ex(a)) ≤a，再结合

所以，∀a∈L，ex1(a) ⊇Ex(a).

综合以上两方面得：∀a∈L，ex1(a)=Ex(a).

再证⊨1=⊨.∀a∈L，∀x∈X.

由定义5，引理6得：x⊨1a，当且仅当x∈ex1(a)，

当且仅当x∈Ex(a)，当且仅当x⊨a.

所以，⊨1=⊨.

从而，两个闭元确定的拓扑系统是一致的.

6 连续映射的等价刻画

本节根据拓扑系统与闭元确定拓扑系统对称性的特点，给出闭元确定的拓扑系统之间连续映射的定义，并利用闭元确定的拓扑系统中的闭包元对连续映射进行等价刻画.

定义8设D=(PtD，ΩD，⊨)，E=(PtE，ΩE，⊨)是闭元确定的拓扑系统，映射Ptf：PtD→PtE和余Frame态射Ωf：ΩE→ΩD构成的偶对(Ptf，Ωf)称为从拓扑系统D=(PtD，ΩD，⊨)到拓扑系统E=(PtE，ΩE，⊨)的映射，记作f：D→E.

再 若∀x∈PtD，∀b∈ΩE，x⊨Ωf(b) 当且仅当Ptf(x)⊨b，则称f：D→E是连续映射.

定理6设D=(PtD，ΩD，⊨)，E=(PtE，ΩE，⊨)是闭元确定的拓扑系统，映射f：D→E连续的充分必要条件是：∀b∈ΩE，ex(Ωf(b))=(Ptf)-1(ex(b)).

证明必要性.∀b∈ΩE，∀x∈PtD，根据定义5，定义8，以及f：D→E连续可知：

x∈ex(Ωf(b))，当且仅当x⊨Ωf(b)，

当且仅当Ptf(x)⊨b，当且仅当Ptf(x) ∈ex(b)，

当且仅当x∈(Ptf)-1(ex(b)).

因此，∀b∈ΩE，ex(Ωf(b))=(Ptf)-1(ex(b)).

充分性.∀b∈ΩE，∀x∈PtD.根据定义5，以及等式ex(Ωf(b))=(Ptf)-1(ex(b))可知：

x⊨Ωf(b)，当且仅当x∈ex(Ωf(b))，当且仅当

x∈(Ptf)-1(ex(b))，当且仅当Ptf(x) ∈ex(b)，

当且仅当Ptf(x)⊨b.

综合以上结果得x⊨Ωf(b)当且仅当Ptf(x)⊨b.

因此，映射f：D→E是连续映射.

定理7设D=(PtD，ΩD，⊨)，E=(PtE，ΩE，⊨)是闭元确定的拓扑系统，f：D→E是连续映射.则以下结论成立：

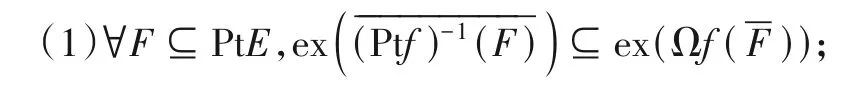
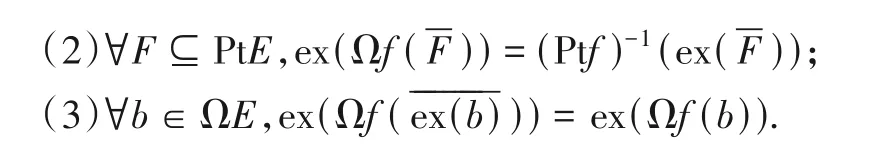
证明（1）∀F⊆PtE，∀x∈PtD.

由定义6 可知：∃b∈ΩE使得F⊆ex(b)，且Ptf(x) ∉ex(b).所以，∃b∈ΩE使得

(Ptf)-1(F) ⊆(Ptf)-1(ex(b))且x∉(Ptf)-1(ex(b)).

由 于f：D→E是连续映射，由定理6 可得ex(Ωf(b))=(Ptf)-1(ex(b)).所以，∃b∈ΩE使得

(Ptf)-1(F) ⊆ex(Ωf(b))且x∉ex(Ωf(b)).

推论1设D=(PtD，ΩD，⊨)，E=(PtE，ΩE，⊨)是闭元确定的拓扑系统，∀F⊆PtE.则

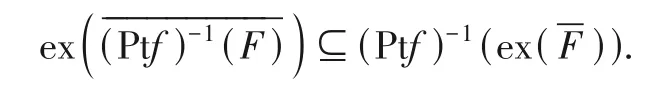
证明结合定理7中（1）、（2）直接可得.

定理8设D=(PtD，ΩD，⊨)，E=(PtE，ΩE，⊨)是闭元确定的拓扑系统.映射f：D→E连续的充分必要条件是下面（1）和（2）同时成立：

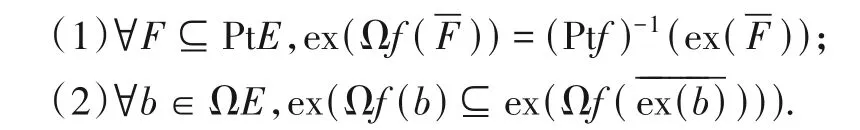
证明必要性.根据定理7（2）、（3）直接可得.

充分性.∀b∈ΩE，则∀ex(b) ⊆PtE，代入（1）得：

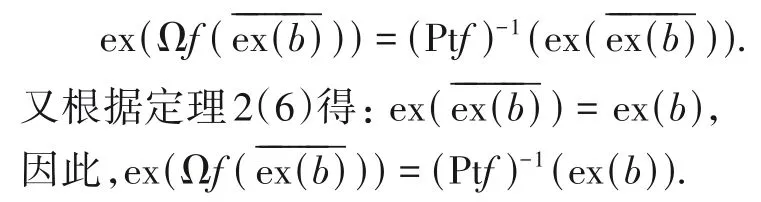
再根据定理2（4）可得：

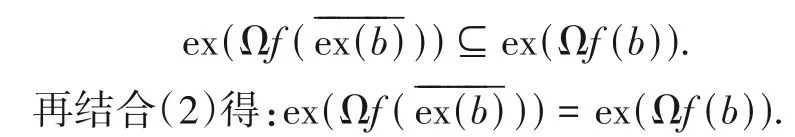
综合上面的等式得：∀b∈ΩE，

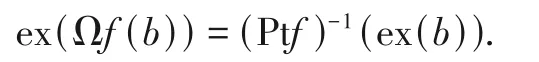
根据定理6得：映射f：D→E是连续的.

注3若f：D→E是拓扑系统D=(PtD，ΩD，⊨)到拓扑系统E=(PtE，ΩE，⊨)之间的连续映射，由推论1知：∀F⊆PtE，

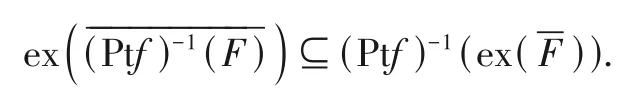
这个结论不是两个拓扑系统之间映射f：D→E连续的充分条件，但这个结论是相应的两个拓扑系统空间化形式之间映射连续的充分必要条件［1］.这个结论体现了拓扑系统中闭包元的作用是点集部分的闭集所不能取代的.