基于多性能约束的连续体结构拓扑优化设计
占金青,彭怡平,刘 敏,黄志超
(华东交通大学 机电与车辆工程学院,江西 南昌 330013)
0 引言
拓扑优化是在给定的结构设计域、作用载荷、固定边界及约束条件下寻求最佳材料分布,使其性能指标达到最优,它是一种非常有效的概念设计方法[1-3]。现有研究大多采用刚度最大化的拓扑优化模型[4-5]获得具有最佳载荷传递路径的拓扑结构,计算效率较高,然而获得的拓扑结构通常不能达到静强度和疲劳性能的要求,难以满足实际工程需要。因此,考虑静强度和疲劳性能约束进行连续体结构拓扑优化设计非常必要。
为了满足静强度要求,需要采用应力约束进行结构拓扑优化设计。DUYSINX等[6]首先采用局部应力约束进行连续体结构拓扑优化研究,然而局部应力约束导致计算效率较低;CHU等[7-8]采用应力惩罚方法处理局部应力约束,进行多相材料结构应力约束拓扑优化设计,避免了大量的局部应力约束;LE等[9]和MENG等[10]采用P范数将大量局部应力约束转为全局应力约束,进行结构全局应力约束拓扑优化设计研究,大大提高了计算效率,但是拓扑结构边界容易出现较多中间密度单元;王选等[11]提出一种改进的双向渐进结构优化法,进行全局应力约束下的柔顺度最小化结构拓扑优化设计,能够减少结构边界出现的灰度单元;占金青等[12]采用可分离插值模型计算多相材料结构的各相材料结构应力,利用全局应力约束方法进行多相材料结构拓扑扑优化设计;易桂莲等[13]引入单元重量惩罚函数和材料许用应力惩罚函数,以构造结构畸变能约束代替应力约束,建立了板壳结构强度拓扑优化模型;LONG等[14]在谐激励作用下进行基于全局动应力约束的结构拓扑优化设计;COLLET等[15]采用qp方法进行周期微结构应力约束拓扑优化设计,能够避免应力约束奇异解问题,而且有效限制了材料微结构的应力水平。
相对于考虑应力约束的拓扑优化问题,有关基于疲劳性能约束的结构拓扑优化设计研究较少。LEE等[16]采用频域疲劳评估方法进行结构疲劳寿命约束拓扑优化设计;叶红玲等[17]引入疲劳寿命过滤函数,提出基于独立、连续、映射方法的结构疲劳寿命约束拓扑优化设计方法;ZHAO等[18]在周期性随机动态载荷作用下,提出基于Crossland准则的结构疲劳约束拓扑优化设计方法;COLLET等[19]提出基于Goodman准则的结构疲劳约束拓扑优化设计方法,将结构疲劳约束转化为局部应力约束。在此基础上,NABAKI等[20]提出连续体结构全局疲劳约束拓扑优化设计方法;侯杰等[21]等在机械连接载荷作用下,将疲劳准则作为设计约束进行结构拓扑优化设计。上述研究仅单独考虑静强度约束或疲劳性能约束进行结构拓扑优化设计,获得的拓扑构型通常难以同时满足静强度和疲劳多性能指标的要求。
为了满足多性能指标要求,本文提出一种考虑静强度和疲劳约束的连续体结构拓扑优化设计方法,以带符号的von Mises等效应力的幅值和均值绝对值之和评定结构静强度,用修正的Goodman疲劳准则评价结构疲劳强度,将结构静强度和疲劳约束分别转化为不同的应力约束,再采用P范数对局部单元应力进行近似最大处理,将多个局部约束转化为全局应力约束,以结构的体积份数最小化为目标函数,建立考虑静强度和疲劳性能约束的连续体结构拓扑优化模型,并将移动渐近线算法用于求解多性能约束优化问题,研究不同幅值和均值参数对拓扑优化结果的影响。
1 结构疲劳分析
假设在正弦载荷作用下,采用准静态分析方法进行有限元分析,有限元平衡方程为
KU=Fmax。
(1)
式中:K为总装刚度矩阵;U为单元节点位移列阵;Fmax为最大载荷列阵。
因此,单元应力及其幅值和均值分别为:
(2)
(3)
(4)

(5)
(6)
式中:Fmax和Fmin分别为正弦载荷的最大值和最小值。

(7)
(8)
由式(8)可知,单元von Mises等效应力总为正值,实际上结构的单元von Mises等效应力均值可能为负值。如果采用恒为正值的von Mises等效应力评估疲劳强度,则不能准确反映结构动特性特征的等效应力。因此,采用带符号的von Mises等效应力[22]表征单元应力均值
(9)
采用修正的Goodman疲劳准则评估疲劳强度,将疲劳性能约束转为单元e(e=1,2,3,…,N)应力约束:
(10)
(11)
式中:σNf为无限循环次数(疲劳寿命次数Nf≥107)下的许用临界应力幅值;σut为拉伸强度;N为有限元单元数。
许用临界应力幅值σNf采用Basquin方程求得:
(12)

2 基于静强度和疲劳性能约束的拓扑优化模型
2.1 拓扑优化模型
采用材料属性有理近似(Rational Approximation of Material Properties, RAMP)模型[23]对单元的材料弹性模量进行惩罚,使任一单元的弹性模量与单元密度呈一定的非线性函数关系:
(13)
式中:Ee为单元的弹性模量;ρe为单元的密度变量,即单元设计变量;k为惩罚因子;E0为实体材料的弹性模量。
为了同时满足静强度和疲劳性能要求,用带符号的von Mises等效应力的幅值和均值绝对值之和评定结构静强度,用修正的Goodman疲劳准则评价结构的疲劳强度,形成由4个L1,e,L2,e,L3,e,L4,e约束和坐标轴围成的安全区域,如图1所示,其中应力约束L1,e和L2,e为疲劳性能约束,L3,e和L4,e为静强度约束。以结构的体积份数最小化为优化目标,建立考虑静强度和疲劳性能约束的结构拓扑优化数学模型:

s.t.
0≤ρe≤1,e=1,2,3,…,N。
(14)
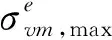
2.2 全局应力约束
为了避免应力约束优化问题的奇异解现象,采用应力松弛方法[25]对单元应力矢量进行惩罚,任一单元的应力可表示为
(15)
式中q为松弛因子,取值为0.5。
由式(14)的数学模型可知,将结构的优化区域划分为N个单元,添加静强度和疲劳性能约束,意味着每个单元都有4个局部应力约束,总的局部约束为4N个,求解灵敏度的计算成本巨大。因此,采用P范数[9]对各类局部应力约束Li,e(i=1,2,3,4)进行近似最大处理,将其转化为多个全局约束优化问题,从而大大提高计算效率。对于任一应力约束Li,e,P范数应力约束值Li,PN可以表示为
(16)
式中p为P范数的参数。
理论上,当参数p趋近无穷大时,P范数应力约束Li,PN(i=1,2,3,4)近似等于对应的最大约束Li,max,然而参数p的值越大,引起多性能约束优化问题的非线性程度越明显,甚至导致优化迭代不收敛[9],因此一般p的取值范围为6~12,本文取p=8,数值算例能够获得很好的拓扑优化结果。
由于p=8,P范数应力约束值Li,PN(i=1,2,3,4)与对应的最大约束值Li,max的差异较大。为此,采用自适应约束缩放方法[26]将P范数应力约束改写为
Li,max=γiLi,PN,i=1,2,3,4。
(17)
式中γi为缩放参数。当迭代步数为n时,
i=1,2,3,4。
(18)
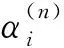

(19)
(20)
2.3 灵敏度分析
采用基于梯度的移动渐近线算法[27]求解考虑静强度和疲劳性能约束的结构拓扑优化问题,需要进行优化目标和约束的灵敏度分析。
结构体积份数对单元密度变量的灵敏度表示为
(21)
由式(14)、式(16)和式(17)求得任一Li,max(i=1,2,3,4)应力约束的灵敏度为
(22)
引入伴随矢量λ,使下列伴随方程成立:
(23)
则有
(24)
由式(14)和式(16)可得Li,PN对ue的偏导:
(25)
(26)
同理可得Li,PN对ρe的偏导:
(27)
(28)
(29)

(30)
(31)

(32)
式中:x和y为任意两个实数;ε为无穷小量。
由式(14)和式(32)有:
(33)
(34)
(35)
(36)
由式(2)可得σe分别对ρe和ue的偏导:
(37)
(38)
由式(13)可得Ke对ρe的灵敏度
(39)

3 数值算例

3.1 L型梁
图2所示为L型梁的设计域、固定边界与载荷条件,尺寸为100 mm×100 mm。L型梁的左上端为固定边界,载荷作用在右下端中点,正弦载荷的最大值为150 N,均匀施加在6单元节点上(如图2的局部放大图),以避免施加集中载荷造成区域应力集中。L型梁设计域划分为6 400个四节点单元。
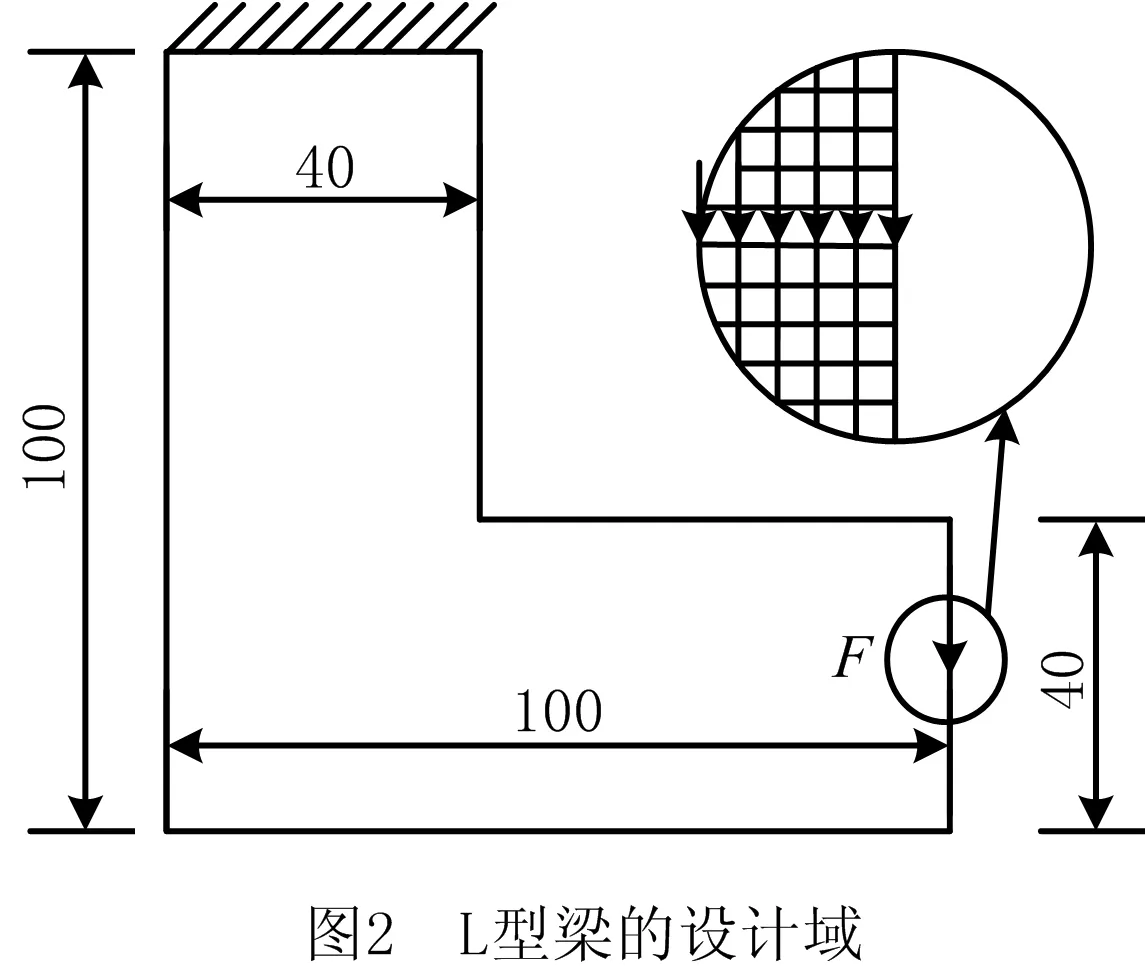
首先,采用基于静强度和疲劳性能约束拓扑优化模型对L型梁进行设计,并与仅考虑刚度优化的拓扑优化结果进行比较。刚度优化设计采用体积约束下的柔顺度最小化拓扑优化模型,结构的体积份数允许值由考虑静强度和疲劳性能约束拓扑优化结果确定,其他所有设计参数的取值均相同,并在相同的正弦载荷条件下采用修正的Goodman图对刚度优化获得的拓扑结构进行疲劳性能评价。在ca=0.4,cm=0.6的正弦载荷条件下,基于静强度和疲劳性能约束的L型梁结构拓扑优化结果如图3所示,仅考虑刚度优化的L型梁结构拓扑优化结果如图4所示,不同拓扑优化模型获得的L型梁优化结果如表1所示。
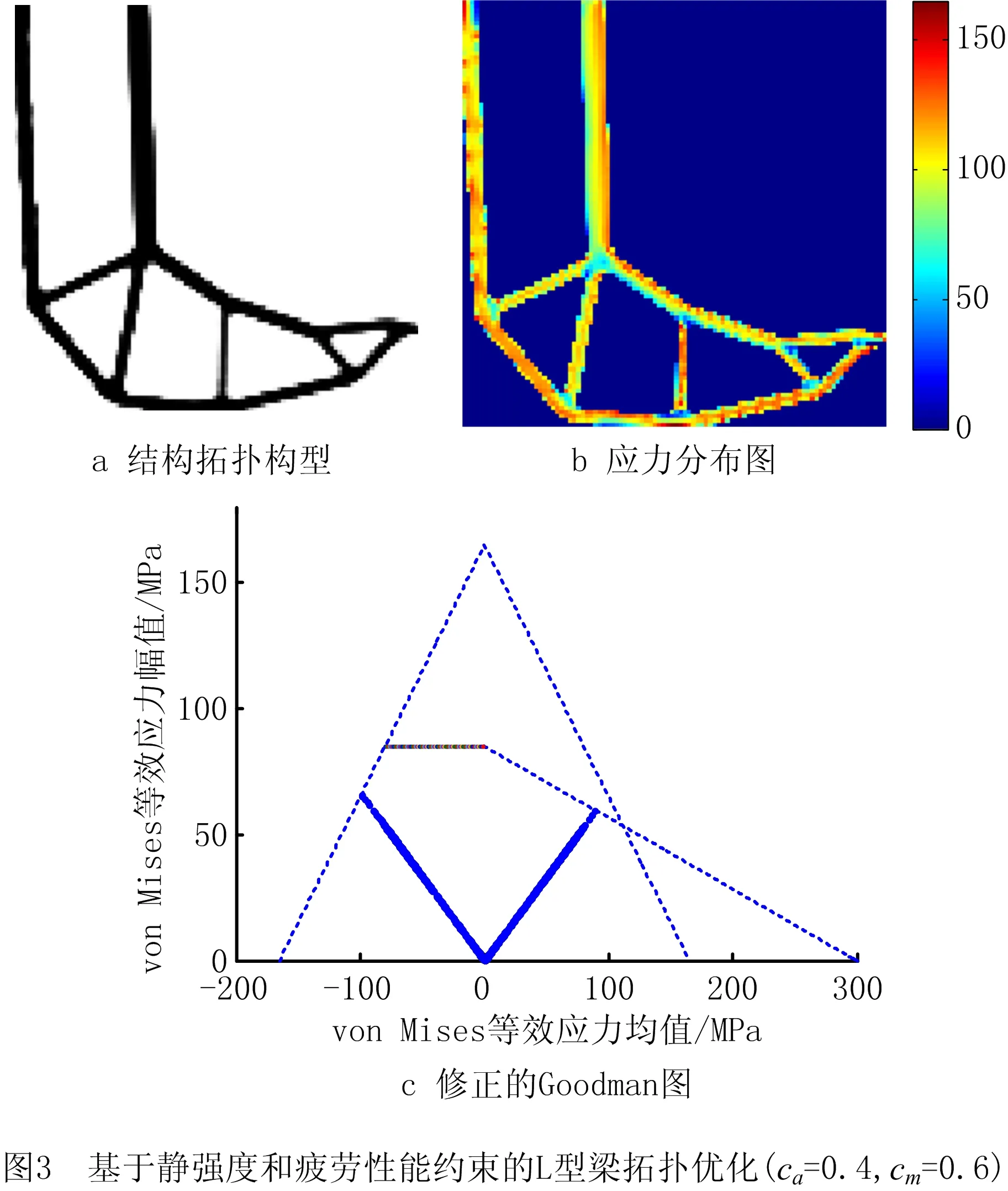
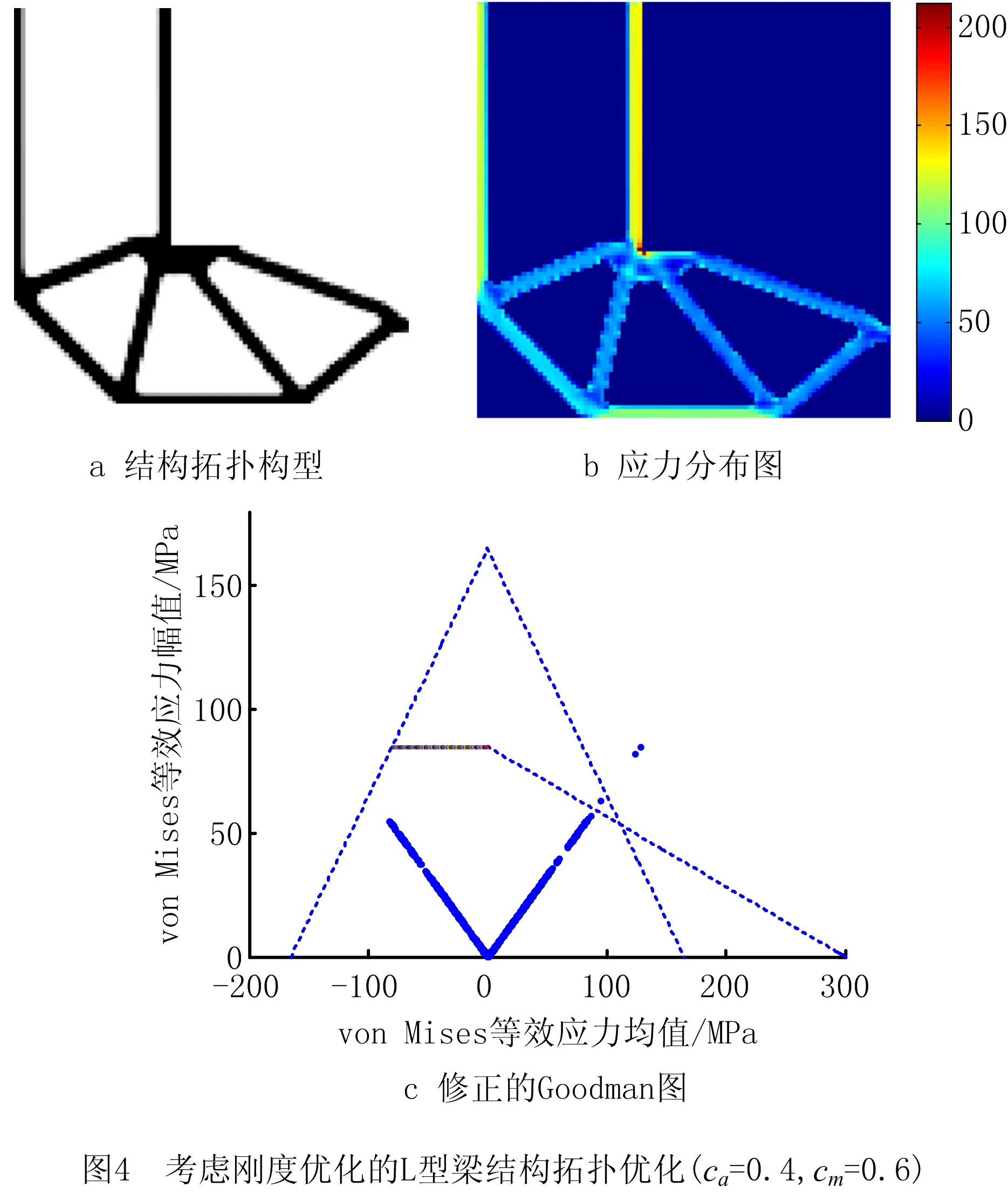

表1 不同拓扑优化模型获得的L型梁优化结果
刚度优化获得的L梁拓扑构型的内凹角拐角区域存在突变边界,导致明显的应力集中现象,结构的最大von Mises等效应力为212.603 MPa,由修正的Goodman图(如图4c)和表1可知获得的L梁拓扑结构不满足L1,e和L3,e应力约束,因此既不能满足静强度又不能满足疲劳性能要求。与刚度优化结果不同,考虑静强度和疲劳性能拓扑优化获得的L型梁拓扑构型,其内凹角拐角区域有近似弧形的结构,能够有效抑制应力集中现象,使应力分布更加均匀,最大的von Mises等效应力为165.054 MPa,由修正的Goodman图(如图3c)和表1可知,所得L型梁拓扑构型满足L1,e,L2,e,L3,e,L4,e4个应力约束,能够同时满足静强度和疲劳多性能指标的要求。
考虑不同幅值系数和均值参数的正弦载荷作用对结构拓扑优化结果的影响,选取(ca=0.2,cm=0.8),(ca=0.6,cm=0.4),(ca=0.8,cm=0.2)3种正弦载荷条件,进行考虑静强度和疲劳性能的L型梁结构拓扑优化设计,L型梁拓扑构型的内凹角拐角区域均出现近似弧形的边界,结构应力分布均匀,分别如图5~图7所示,不同正弦载荷条件下的L型梁优化结果如表2所示;由修正的Goodman线图(图5c、图6c和图7c)和表2可知,3种载荷条件获得的L型梁拓扑构型均满足L1,e,L2,e,L3,e,L4,e4个应力约束,能够同时满足静强度和疲劳多性能指标的要求。随着正弦作用载荷的幅值系数ca的增加,L型梁拓扑结构需要更多用材,以同时满足静强度和疲劳性能的要求。
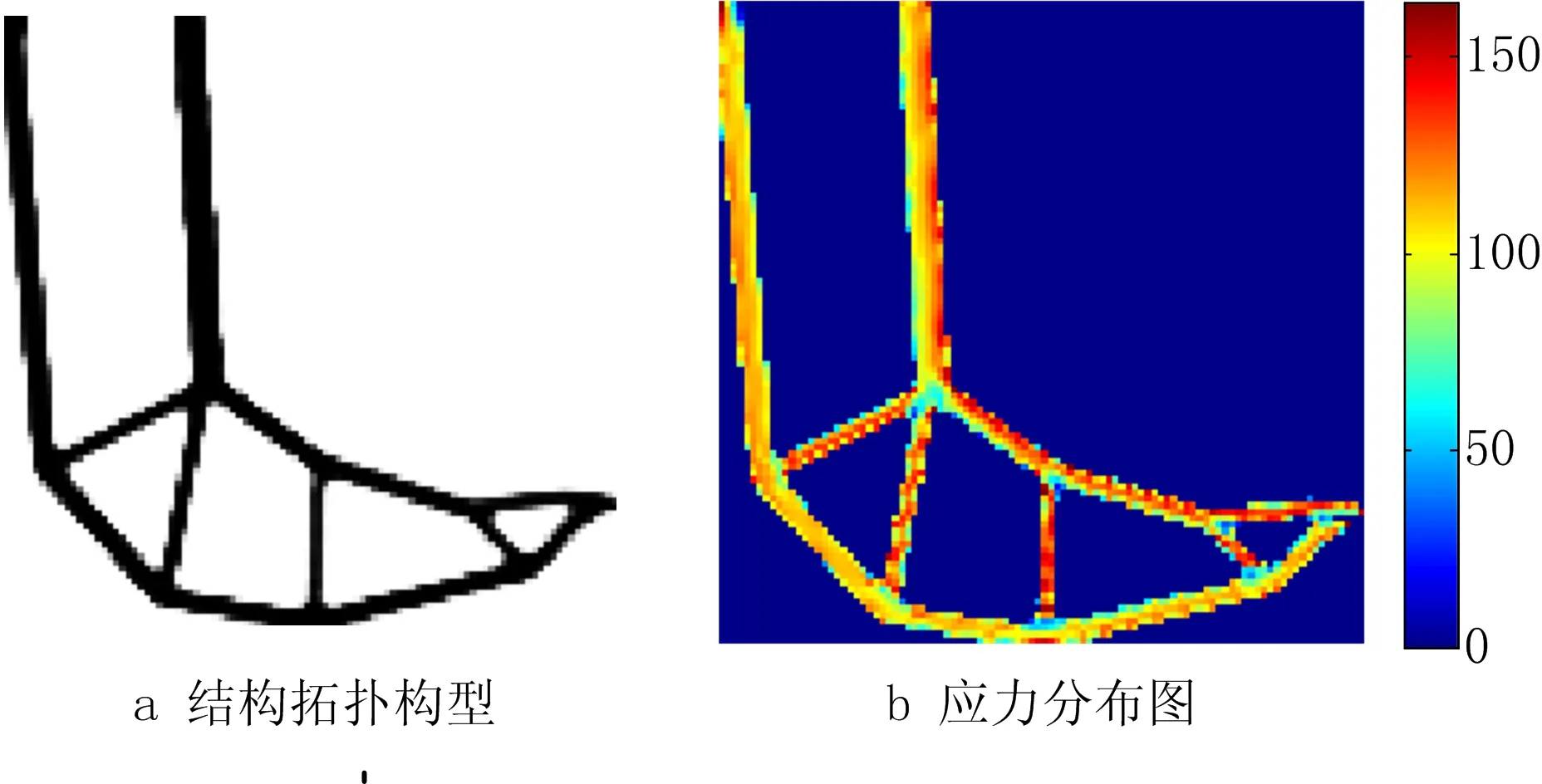

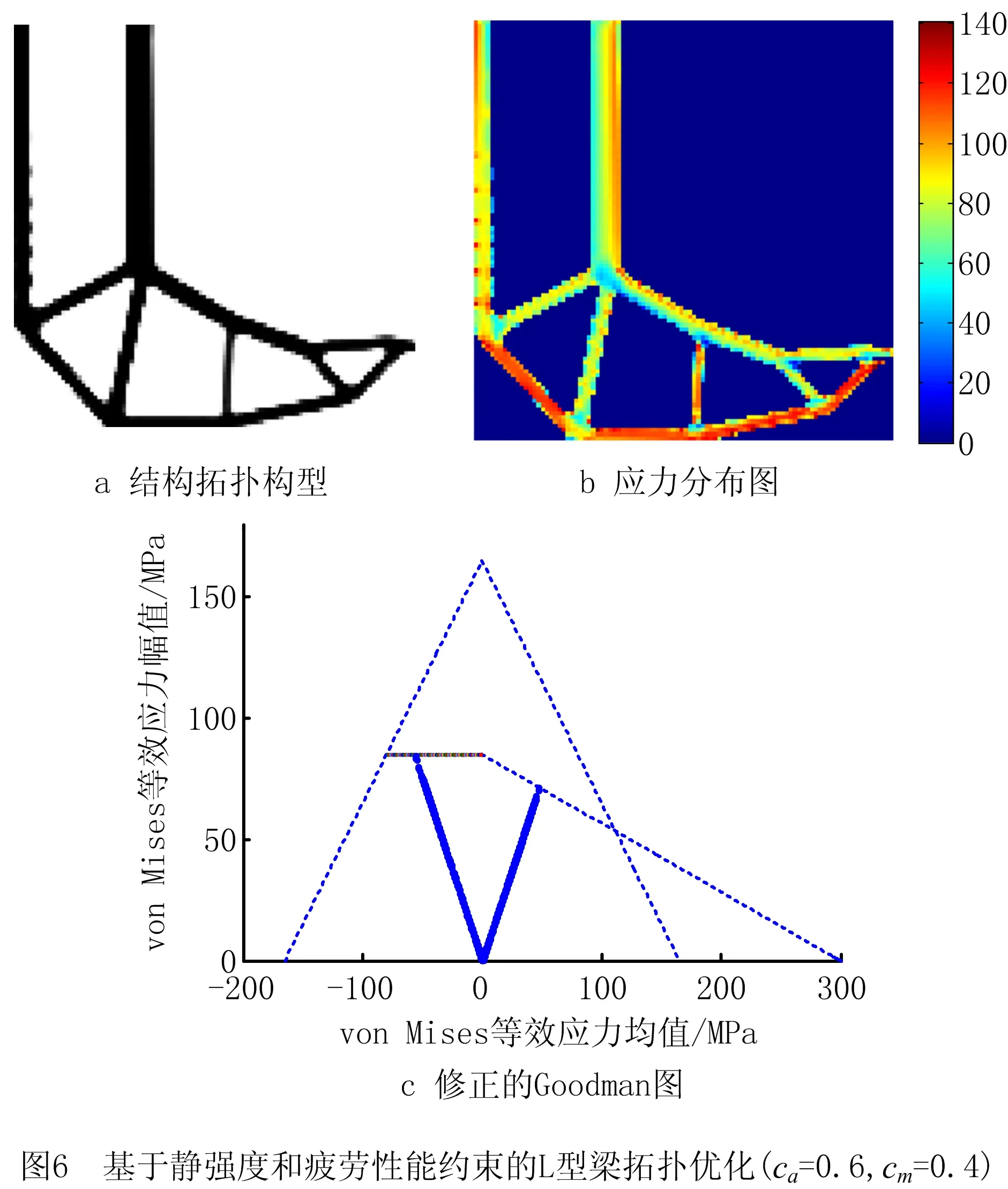
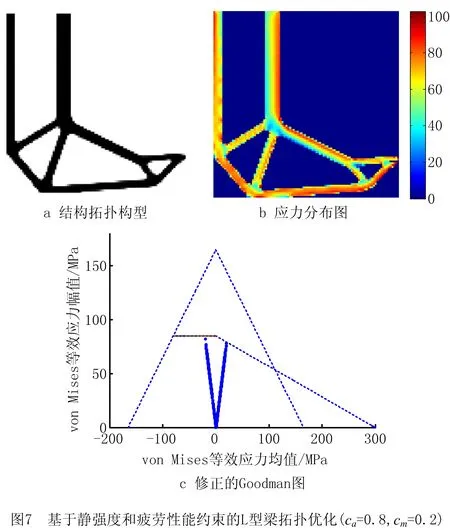
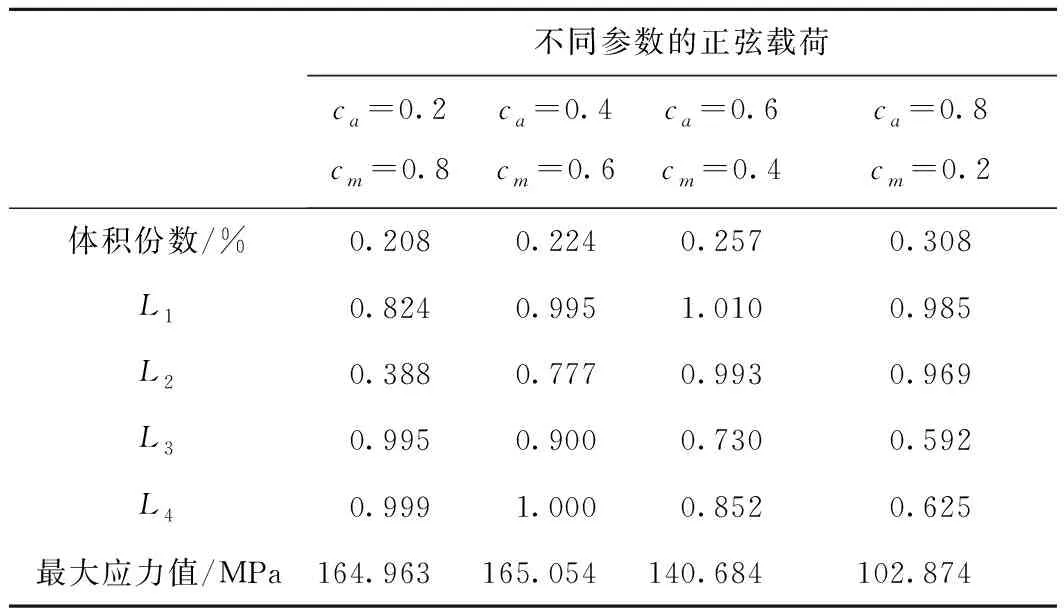
表2 不同正弦载荷条件下的L型梁优化结果
3.2 悬臂梁
图8所示为悬臂梁的设计域、固定边界和载荷条件,尺寸为100 mm×50 mm,其左端为固定边界,载荷作用在右下端,正弦载荷的最大值为150 N,均匀分布在六单元节点上,设计域划分为5 000个四节点单元。

在σa=0.5,cm=0.5正弦载荷条件下,进行考虑静强度和疲劳性能的悬臂梁拓扑优化设计,优化结果如图9所示,仅考虑刚度优化的悬臂梁拓扑优化结果如图10所示,不同拓扑优化模型获得的悬臂梁优化结果如表3所示。刚度优化获得的悬臂梁拓扑构型存在明显的应力集中现象,最大应力集中在固定边界区域,最大的von Mises等效应力为243.369 MPa;由修正的Goodman图(如图10c)和表3可知,获得的悬臂梁结构不满足L1,e,L2,e,L3,e,L4,e4个应力约束,既不能满足静强度又不能满足疲劳性能的要求。不同于刚度优化,考虑静强度和疲劳性能拓扑优化获得的悬臂梁拓扑构型的应力分布更加均匀,其最大的von Mises等效应力更小,为164.439 MPa;但是由于存在较小尺寸的空洞,可能给制造加工带来一定困难,可以添加制造尺寸约束来消除空洞。同样地,由修正的Goodman图(如图9c)和表3可知,优化获得的悬臂梁拓扑结构很好地满足了L1,e,L2,e,L3,e,L4,e4个应力约束,说明其能够同时满足静强度和疲劳多性能指标的要求。

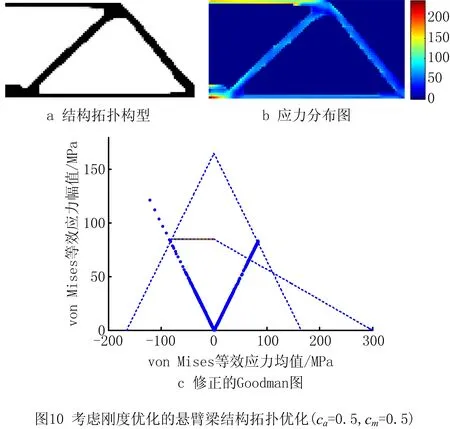

表3 不同拓扑优化模型获得的悬臂梁优化结果
同样选取σa=0.3,cm=0.7和σa=0.7,cm=0.3两种正弦载荷条件,进行考虑静强度和疲劳性能的悬臂梁拓扑优化设计,获得的悬臂梁拓扑构型分别如图11和图12所示,结构的应力分布均匀,不同正弦载荷条件下的悬臂梁优化结果如表4所示。由修正的Goodman图(如图11c和图12c)和表4可知,这两种正弦载荷条件下获得的悬臂梁拓扑结构均满足L1,e,L2,e,L3,e,L4,e4个应力约束,能够同时满足静强度和疲劳多性能指标的要求。随着正弦作用载荷幅值系数ca的增加,悬臂梁拓扑结构需要更多用材,以同时满足静强度和疲劳性能的要求。
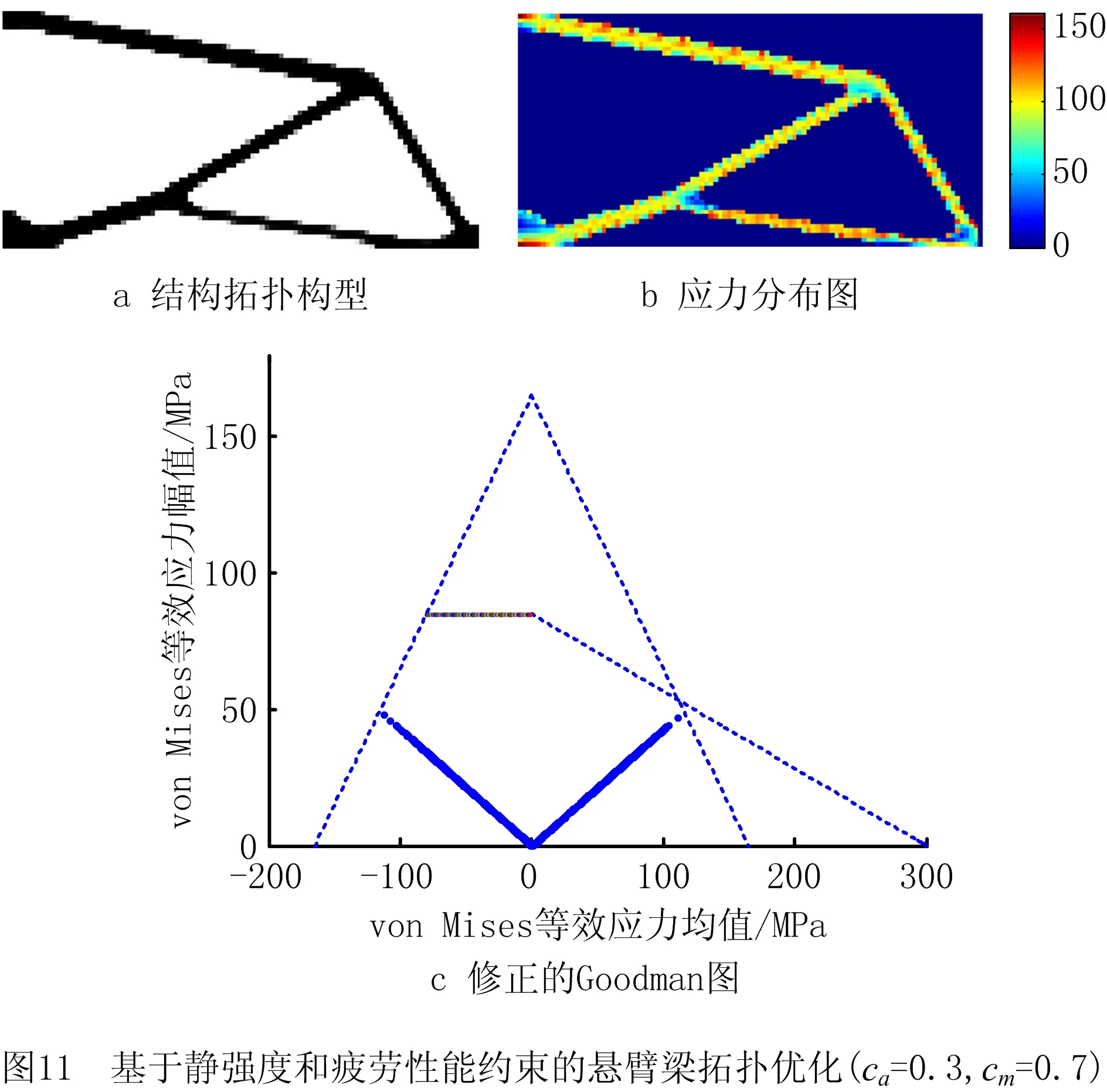
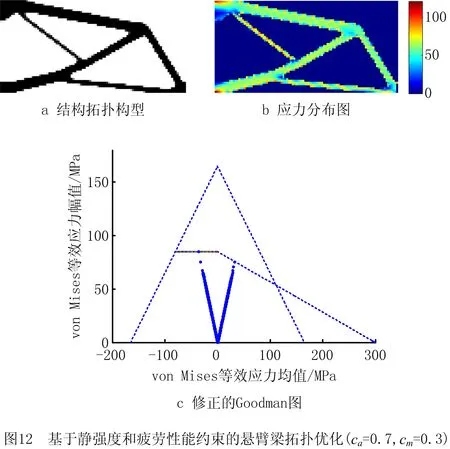
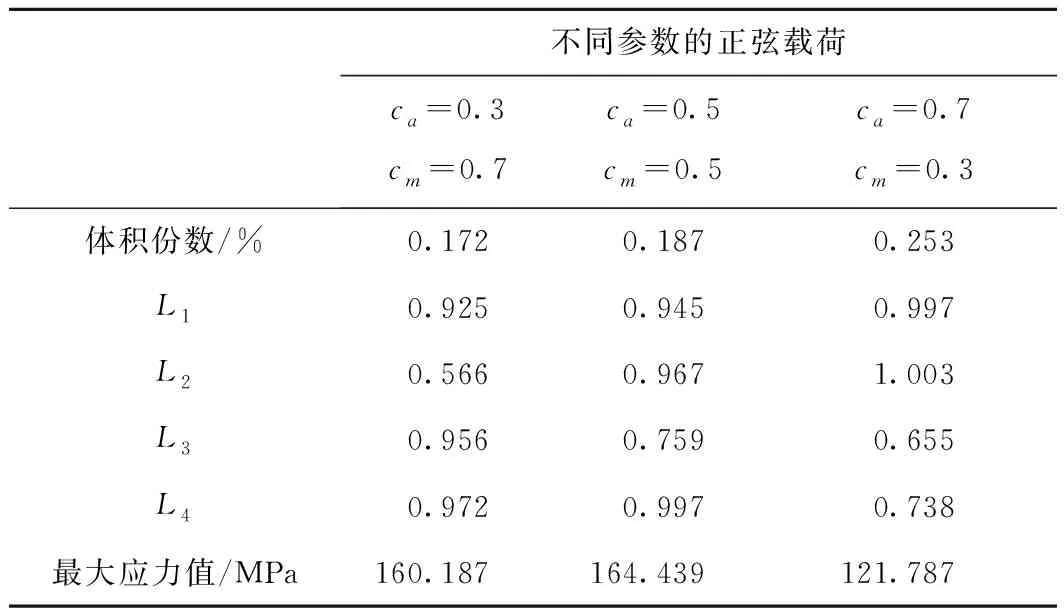
表4 不同正弦载荷条件下的悬臂梁优化结果
4 结束语
本文提出一种基于多性能约束的连续体结构拓扑优化设计方法。该方法以结构的体积最小化为优化目标函数,以结构静静强度和疲劳强度为约束,采用P范数将结构静强度和疲劳局部约束转化为多个全局应力约束,实现了同时考虑静强度约束和疲劳约束的连续体结构拓扑优化设计,并通过数值算例验证了所提方法的有效性。
数值算例表明,不同于仅考虑刚度优化,考虑静强度和疲劳性能拓扑优化获得的结构拓扑构型能够同时满足静强度和疲劳多性能指标的要求,并有效抑制应力集中现象,使结构的应力分布更加均匀,最大的von Mises等效应力更小;随着正弦载荷幅值系数的增加,基于静强度和疲劳性能约束拓扑优化获得的拓扑结构需要更多用材,以同时满足结构的静强度和疲劳多性能指标的要求。然而,本文方法获得的拓扑结构存在不光滑的锯齿边界,如何将所提优化模型与水平集方法结合进行多性能约束的连续体结构拓扑优化设计,获得具有光滑边界的拓扑结构,将是今后的工作重点。

