基于栅格空间的自适应GB_RRT*机械臂路径规划

张立彬,林后凯,谭大鹏

(浙江工业大学 机械工程学院,浙江 杭州 310014)

0 引言

面向智能制造2025，我国智能机器人技术正处于从低端制造向智能化、精益化制造转型时期。作为智能机器人的一种，移动机械臂可以代替人在救灾、采矿、高空装配、检测焊接、行星探测等危险环境中工作[1-4]。由于移动机械臂作业的工作环境并不固定，针对环境变化快速做出反应并寻找通往目标点的无碰撞较优路径成为当前机械臂避障技术攻关的难点，开展不同复杂障碍物环境下机械臂的快速避障路径规划具有重要的工程意义[5-7]。

避障路径规划指在工作空间存在障碍物的情况下，机器臂在较短时间内规划一条从起始点到目标点的无碰路径[8-11]。因为机械臂属于高维本体结构，所以路径规划时复杂度较高，目前在国内外提出的多种规划方法中比较优秀的有采样法和局部规划法[12-13]。KALA[14]提出随机路标图法(Probabilistic Roadmap, PRM)，其采用完全随机采样策略将连续空间转换为离散空间来构建路径网络图，再采用A*等搜索算法在路线图上快速规划无碰路径；曹博等[15]提出改进人工势场法(Artificial Potential Field, APF)，在机械臂关节空间内建立目标角度引力势场，在笛卡尔空间内建立末端引力势场和障碍物斥力势场，通过所有势场共同作用引导机械臂运动；AKGUN等[16]结合快速搜索随机树算法(Rapidly exploring Random Tree star, RRT*)提出渐进最优的B-RRT*(bidirectional RRT*)，其用RRT*代替RRT扩展找到初始路径后，设定采样约束减少无效节点，通过局部偏置优化路径上的节点至局部最优；谢碧云等[17]提出双树随机树搜索(bi-directional Rapidly-exploring Random Tree, bi-RRT)算法，该算法结合末端姿态调整和关节自运动，利用对机械臂逆解生成目标点的树根，在给定的障碍物环境中自动选择某一合适的位形作为目标节点来引导搜索树最有效地生长；李洋等[18]提出引力自适应步长RRT在工作空间对步长进行有效约束，减少了迭代次数，降低了运行时间并缩短了路径长度；刘晓倩等[19]提出融合目标偏向优点的目标偏向快速搜索随机树(Goal Bias Rapidly-exploring Random Tree, GB_RRT)，通过提升RRT的导向性来减少搜索树叶节点的数量，从而提高RRT搜索树的效率。

通过上述分析可以发现，避障路径规划技术在机械臂运动领域获得了广泛应用，并取得较好的研究结果，然而上述研究多集中于提升某一特性，尚不能适应不同的复杂障碍物环境。基于完全随机采样的RRT，PRM，RRT*，B-RRT*和引力自适应步长RRT在多障碍物环境下优势明显，但在救灾、采矿、高空装配、焊接、行星探测等简单障碍物工作环境下，因为机械臂采用随机采样策略，所以难以在较短的时间内规划出较优的路径。GB_RRT*和APF算法虽然在简单障碍物环境中的规划性能较好，但是APF算法在多障碍物环境工作时容易陷入局部极值点，使所规划的路径代价过高，而GB_RRT*算法在多障碍物环境下因存在“徘徊探索”现象而导致搜索时间过大。

针对上述问题，本文采用基于栅格空间的自适应目标偏向快速扩展随机树算法(Rapidly exploring Random Tree Star Algorithm for adaptive Goal Bias based on grid space, SAGB_RRT*)在关节空间对移动机械臂进行避障路径规划：①结合RRT*渐进最优思想对GB_RRT进行优化，使搜索路径朝渐进最优解收敛；②通过栅格储存树节点并结合栅格快速查找相邻节点来提升算法效率；③利用open表解决目标偏向采样策略引起的重复偏向问题；④结合open表节点数量控制偏向性生长值来缩减无效扩展，降低搜索时间和路径代价；⑤采用可变间隔的贪心算法进一步改善规划所得路径的曲折性，并降低规划所得的路径代价。与其他避障路径规划算法相比，本文算法在不同复杂障碍物环境下能够用更短的规划搜索时间规划出更优的避障路径。本文研究可以为路径规划领域的理论研究提供有益的参考，也可以为智能机器人的系统研发提供技术支持。

1 GB_RRT*算法原理

GB_RRT*算法是结合RRT*渐进最优思想对目标偏向RRT进行优化，使搜索路径朝渐进最优解收敛，其主要通过扩展随机树、重选父节点和重布线对避障路径进行优化[20-21]。

如图1所示，扩展随机树时首先将初始节点Xinit作为所构建随机树T的根节点，在扩展下一节点时主要采用目标偏向阈值P控制采样节点Xrand的生长，来影响随机树扩展的方向，降低了随机树搜索过程中的无目的性。阈值P对采样节点Xrand的控制是通过比较随机产生概率Prand和阈值P的大小来实现，主要有两种情况：

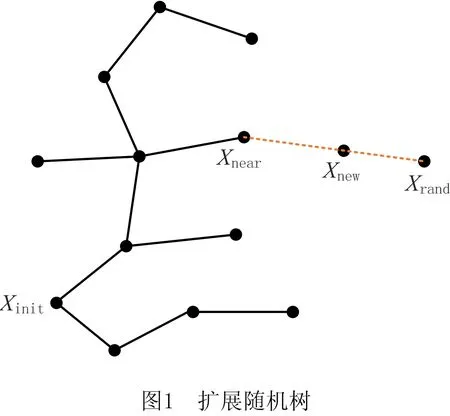
(1)当Prand≥P时，随机树倾于向未探索过的空间扩展，即在空间中随机选择任意状态点作为Xrand。

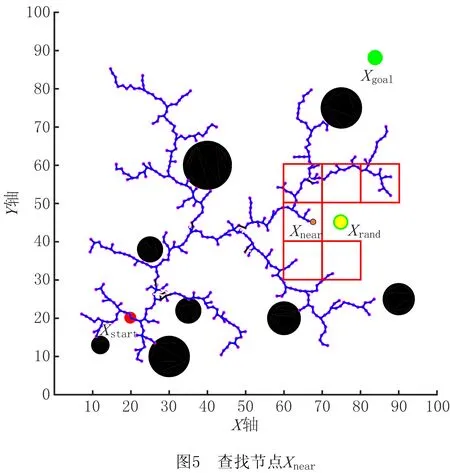
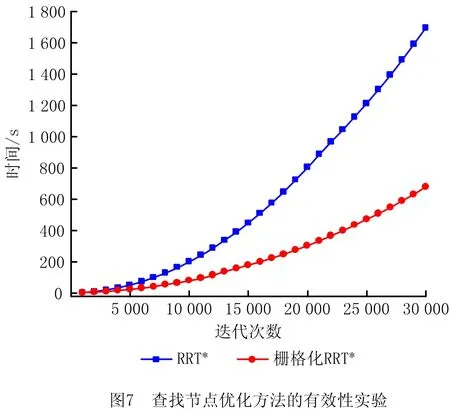
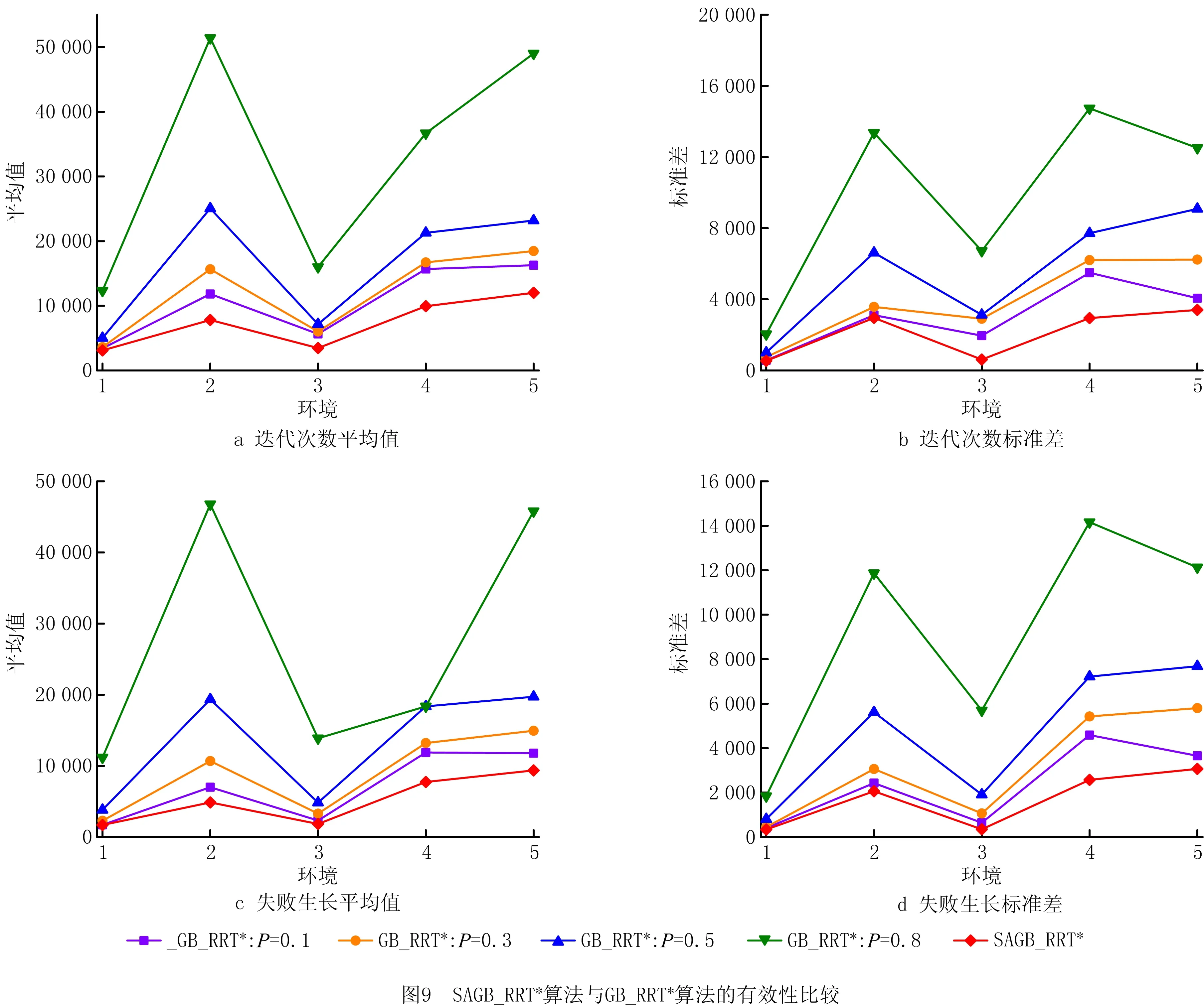
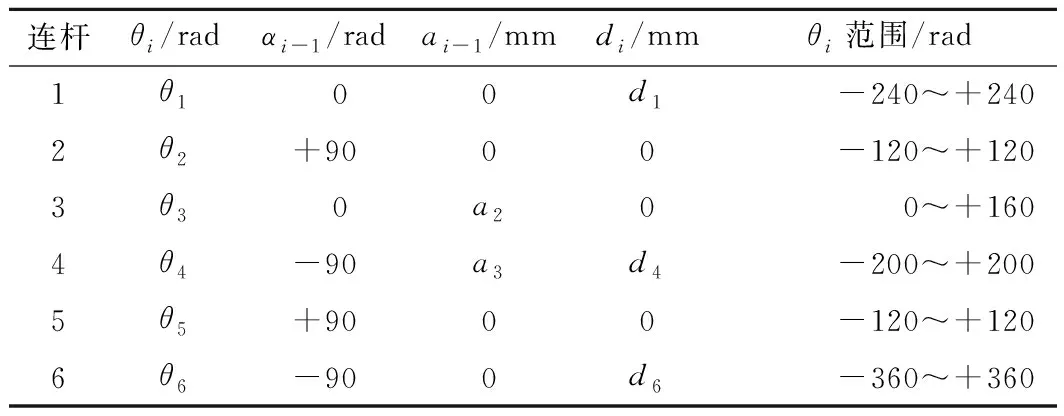
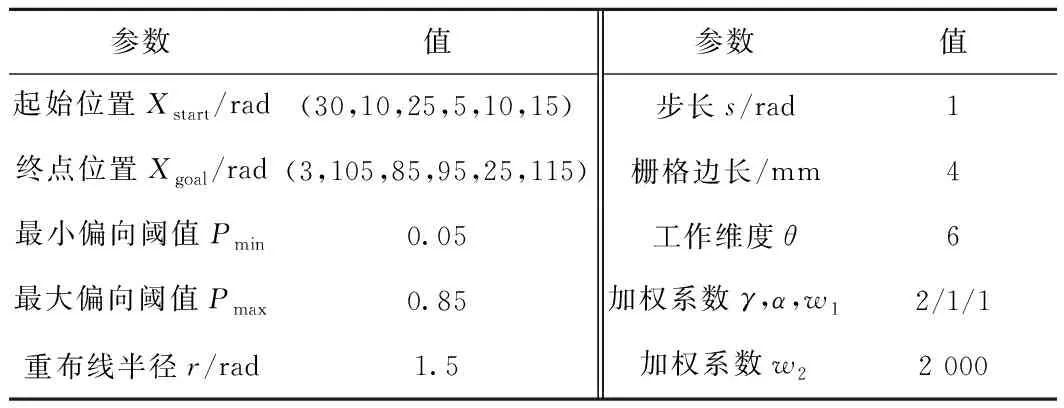
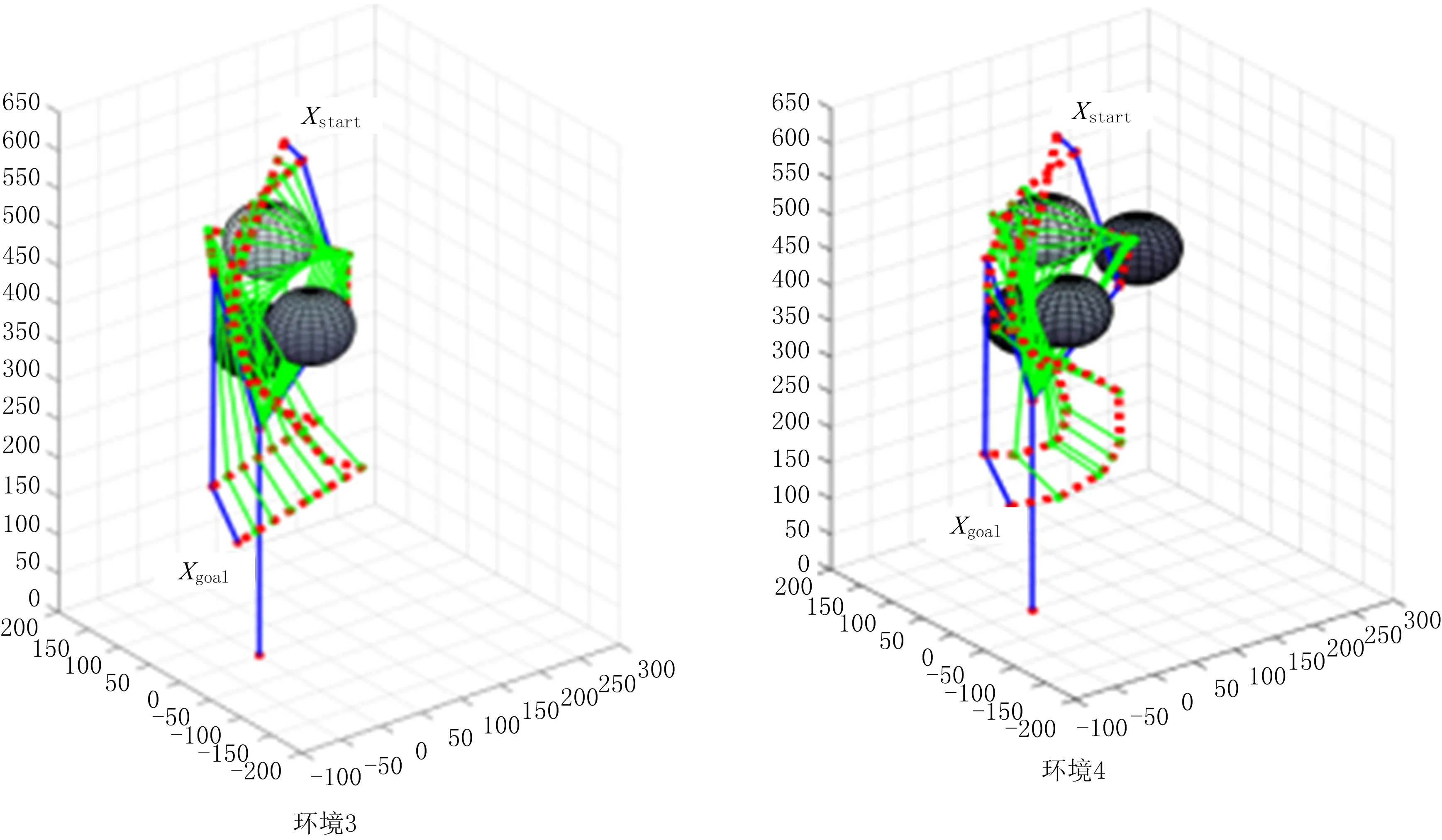
(2)当Prand

通过上述方式确定Xrand后，遍历随机树找到距离Xrand最近的树节点Xnear，在碰撞检测合格后经固定步长扩展得到新节点Xnew，然后将Xnew添加到随机树中并记录其父节点和节点权值。

如图2所示，重选父节点的意义在于通过邻域r内的其他节点降低Xnew节点的权值。首先计算Xnew连接邻域r内所有节点的权值，若存在能使Xnew权值更小且不碰撞的Xmin节点，则删除Xnew与原父节点的连线，同时将Xmin节点作为新的父节点，更新Xnew的权值。

如图3所示，重布线过程的意义在于通过Xnew降低其他节点的权值，在不与障碍物碰撞的前提下，若其他节点通过将Xnew作为父节点来降低权值，则将Xnew节点作为其新父节点并更新节点权值。

2 SAGB_RRT*算法

虽然GB_RRT*算法具有渐进最优的特点，但是在为移动机械臂规划时无法给予CPU足够的运算时间，而且在不同环境下无法变换目标偏向阈值，缺乏对环境的适应性，造成算法无法在不同复杂障碍物环境下用较短的时间规划出较优的避障路径[22]。本文基于GB_RRT*框架，提出适合移动机械臂在救灾、采矿、高空装配、焊接、行星探测等环境下的SAGB_RRT*(grid space-based adaptive goal bias rapidly exploring random tree star)运动规划算法，该算法在原算法概率完备和渐进最优性不变的前提下，通过构建全状态空间栅格地图的数据存储结构优化查找相邻节点的方法来提升计算速度，采用open表生长策略优化随机树的生长方式以避免重复偏置并控制偏向性生长，结合可变间隔贪婪算法以快速优化已规划路径，使机械臂在适应各种环境的同时能用较短的搜索时间规划出较优的避障路径。

2.1 节点查找优化

机械臂属于高维本体结构，为其规划路径时需要数量庞大的树节点，造成GB_RRT*算法全遍历查找相邻节点的复杂度呈指数上升，导致算法搜索时间爆炸式增长。为避免原算法在查找相邻节点时遍历所有树节点的时间代价过大，本文算法结合工作空间的大小构建全状态空间的栅格地图来存储数据，通过映射方式分块整理树节点，并通过查找栅格遍历部分树节点，从而降低算法搜索时间。

在二维空间内对栅格地图的原理进行表述，如图4所示，在确保小栅格边长s大于步长λ和重布线半径r的前提下，结合工作空间大小确定栅格s的值后构建栅格地图。

构建栅格地图后，每个节点存储时都有对应的栅格，通过各轴向划分栅格数和节点栅格坐标得到节点的栅格索引值，可以实现节点和栅格索引值的映射。随机树任意节点的栅格坐标均由其已知工作空间坐标换算得到，具体为：

(1)

(2)

式中：函数int表示对所求值取整；(x0，y0)为节点位置坐标，(x，y)为树节点栅格坐标；s为每个小栅格的边长。

通过构建映射关系快速查找相邻节点的原理如图5所示，在扩展生长和重选父节点查找Xnear时，改进算法只需通过映射关系得到其栅格索引值，即可快速查找Xrand周边的栅格群，然后在Xrand周边栅格群遍历查找树节点Xnear。如图6所示，在重布线阶段查找χnear时，改进算法通过映射关系得到的栅格索引值快速查找到Xnew周边栅格群，然后在Xrand周边栅格群遍历查找树节点群χnear。

本文通过优化节点查找方式提升规划效率。因为构建栅格地图只是简单地根据工作空间确定每个小存储栅格的大小，相比全遍历树节点查找相邻节点的方式，其在时间和空间的复杂度基本忽略不计，所以对算法规划性能的分析更多在查找相邻节点的时间和空间复杂度上。然而，随着随机树的不断生长，树节点不断增多，原算法在扩展生长、重选父节点和重布线时查找相邻节点所采用的方式是遍历所有树节点，其时间复杂度与树节点个数为指数倍关系，改进算法只需从当前节点所在栅格与其周边栅格中的树节点遍历查找相邻节点，时间复杂度维持在一定范围内，大大降低了时间复杂度。

为了验证查找节点优化方法的有效性，在障碍物、步长等条件均相同的情况下，分别采用原算法和GB_RRT*算法对6关节机械臂进行规划。比较相同迭代次数所用的CPU计算时间如图7所示，可见在相同迭代次数下，基于栅格化RRT*所需的搜索时间明显小于RRT*算法，其中当迭代次数为30 000时所需的搜索时间从1 695.84 s下降到679.17 s，降低了65%，可知结合工作空间的大小构建全状态空间的栅格地图进行节点的相互映射，通过映射关系快速查找相邻节点的方法能够有效降低算法因树节点数量增加而导致的计算量指数爆炸问题，从而证明本文查找节点优化方法的有效性。

2.2 生长方式优化

GB_RRT*算法在规划时由于目标偏向会出现重复，造成时间浪费。当选择的P值较低时，由于随机树生长偏向性弱，GB_RRT*算法在简单环境中会进行大量无效搜索；当P值较高时，由于随机树生长偏向性强，GB_RRT*算法在复杂情况下，尤其是障碍物遮挡目标时，极易陷入局部偏向而重复产生大量失败的生长，使算法对环境的适应性较差。为避免重复偏向并保证随机树生长时对环境有较强的适应性，引入自适应学习的思想并构建可存储目标偏向生长点的open表，将成功扩展所得的Xnew作为目标偏向生长点存入open表，在进行随机树扩展时，从open表中查找离Xgoal最近的Xnear节点生长,不管生长能否成功均将Xnear节点作为不可偏向生长点从open表中删除，通过节点扩展时的搜索方向和反馈的搜索状态控制open表中的节点数量来控制目标偏向阈值的变化，从而自适应调整目标偏向阈值P。

通过自适应调整P值来增强算法对环境的感知能力，其原理在于，open表中的节点数量越大，可偏向生长的树节点越多，应该缩减随机树探索未知空间的能力，而将主要精力放在目标偏向生长上，即增大P值；open表中的节点数量越少，可偏向生长的树节点越少，继续向目标偏向生长极易造成堆积在障碍物附近的树节点过多，因此当节点数量较少时，应增强随机树探索未知空间的能力，避免随机树陷入局部障碍物处难以自拔，即减小P值。图8所示为自适应调整目标偏向阈值P的基本框架。

由于SAGB_RRT*算法在规划时对open表中节点的数量完全可知，可以通过调节open表中的节点数量在某一范围内自适应调整目标偏向阈值P，即

(3)

式中：Pmin为目标偏向的最小阈值，Pmax为目标偏向的最大阈值；Knode为open表中当前节点的数量；Kmax为open表中所能存放节点数量的最大值，

(4)

式中：α为系数；‖Xgoal-Xstart‖为欧拉范数定义的目标点到起点的距离；γ为机械臂关节维度的权值；θ为工作空间的维度；λ为随机树扩展的步长。

由式(3)和式(4)可知，引入自适应学习思想生成目标偏向阈值P的表达式为

P=Pmin+(Pmax-Pmin)·

(5)

采用上述方式，结合open表使随机树在未偏向生长的节点中选择偏向生长，以避免随机树重复偏向生长，从而缩减无效扩展，提升算法效率。通过自适应调整目标偏向阈值P，使算法在规划时能够用更少的迭代次数、更强的偏向性令路径快速收敛。

为进一步证明优化SAGB_RRT*算法生长方式的效果，在5种不同环境下分别采用SAGB_RRT*算法和不同阈值的GB_RRT*算法进行规划，如图9所示。由于两种算法均基于采样使规划结果具有不确定性，为使实验结果更具说服力，每个算法均仿真分析15次，结果取平均值。由图9a和图9c可见，在5种环境下，SAGB_RRT*算法更优的原因在于引入open表解决了偏向重复，同时采用目标阈值P自适应优化了生长方式；由图9b和图9d可见，相比GB_RRT*算法，SAGB_RRT*算法所需的树节点和失败生长点均较少，证明了本文SAGB_RRT*算法的有效性。

2.3 路径优化

GB_RRT*是基于随机采样的搜索算法，虽然利用目标偏向生长和重布线策略进行优化，但是仍然存在曲折路径，造成最终规划的路径代价较高。贪婪算法能够对已知路径进行贪心优化，使其不断接近最优解，为了能在较短时间内使路径总代价最低，引入可变间隔m的贪心算法对SAGB_RRT*算法规划得到的路径进行快速优化，其中路径代价目标函数

(6)

式中：C为机械臂相邻关节角的路径代价；θi为机械臂的第i关节角。

利用可变间隔m的贪心算法对已知路径进行优化，首先将Xinit作为起始节点，为保证算法的时效性，依次优化从起始节点到相隔m值的后续节点的路径，将起始节点和后续节点通过正运动学求解后得到机械臂的运动状态，并在笛卡尔空间求得机械臂在该运动路径下的碰撞情况。当与障碍物碰撞时，结合起始节点的当前后续节点和上个后续节点依次逆向查找，若从起始节点到所查节点的路径与障碍物不碰撞则停止搜索。将起始节点与该节点相连作为新的路径，以该节点为起始节点继续进行间隔m的贪婪搜索，如此反复直到终点，停止搜索。

通过上述方法优化已知路径，当已知路径中的障碍物较少时采用较大的可变间隔，以减少碰撞检测次数，加快规划速度，因此应根据起始目标距离、所得路径和搜索时的失败生长点数选择m值，具体为

(7)

式中：dist(path)为已规划路径；dist(Xgoal,Xstart)为起点到终点的距离；Qinvalid为失败生长节点数。

3 算法实现

基于上述改进思想，为保证移动机械臂在救灾、采矿、高空装配、检测焊接、行星探测等危险环境中能够用较短的搜索时间快速规划较优的避障路径，提出一种避障规划SAGB_RRT*算法，其伪代码如下：

算法1SAGB_RRT*。

1. Wg←Workspace_Grid(W)

2. T←Initialize_Tree()

3. For k=1:k do

4. P←Update_P(Kopen,Kmax)

5. Prand←rand(0～1)

6. If Prand>P

7. Xrand←Random_State()

8. else

9. Xrand←Xgoal

10. χrandgrids←Find_Grids_Near(Xrand,Wg)

11. Xcloset←Find_nodes_Near(χrandgrids,Xrand)

12. Xnew←Steer(Xrand,Xcloset,λ)

13. If Obstacle_Free(Xnew)

14. Xnew←New_State(Xcloset,λ),Open←Add(Xnew)

15. If Xrand=Xgoal

16. Open←Delete(Xcloset)

17. Xmin=Xnear,Cmin=cost(Xnear)+dist(Xnear,Xnew)，Xnewparent←Xcloset

18. χnewgrids←Find_Grids_Near(Xnear,Wg)

19. χnear←Find_nodes_Near(χnewgrids,Xnew,r)

20. For Xnear∈χneardo

21. Cnew=cost(Xnear)+dist(Xnear,Xnew)

22. If Cnew

23. Cmin=Cnew,Xmin=Xnear,Xnewparent←Xnear

24. For Xnear∈χneardo

25. Cold=cost(Xnew),Cnew=cost(Xnear)+dist(Xnear,Xnew)

26. If Cnew

27. Cmin=Cnew,Xmin=Xnew,Xnewparent←Xnew

28. If dist(Xnew,Xgoal)≤r and line(Xgoal,Xnew)∈Xfree

29. path←Getpath()

30. Break

31.Path←GreedyOptimize(path)

SAGB_RRT*算法进行路径规划的主要步骤为：第1步结合工作空间划分栅格空间，并利用栅格存储和映射关系快速查找相邻节点；第2步初始化时，定义6关节移动机械臂的起始关节数组Xstart、目标关节数组Xgoal和关节搜索步长λ；第3步～第9步通过反馈open表中的可扩展节点数来更新目标偏向阈值P，比较随机概率Prand和P的大小确定随机节点的Xrand，通过Xrand控制随机树的生长；第10步～第12步为了快速扩展节点Xnew，利用Xrand所在栅格的索引值在栅格空间快速查找离Xrand所在栅格最近且含有树节点的栅格群，在这些栅格群中迅速找到离Xrand最近的节点Xcloset，利用Xcloset生长一个步长得到Xnew；第13步～第16步对Xcloset～Xnew的运动进行碰撞检测，在碰撞检测合格的前提下按照Xnew生长结果更新open表，从而避免随机树重复偏向生长；第17步～第23步通过Xnew重选父节点策略来优化路径，其关键为在节点Xnew通过其他节点获得更低权值时，更新父节点并更新权值，主要创新为结合栅格群χnewgrids快速找到Xnew相邻节点群χnear；第24步～第27步通过重布线优化路径，然后结合相邻节点群χnear找到Xnew相邻半径r内通过Xnew获得更低权值的节点，更新父节点和权值；第28步～第30步为算法循环停止的条件，当Xnew距离Xgoal小于r且与Xgoal连线和障碍物不碰撞时得到避障路径，循环停止；第31步用间隔m贪心算法快速优化SAGB_RRT*已规划出的路径，使所规划的路径代价更加接近最优解。

4 仿真与实验

为验证算法性能，以日本三菱公司RV-2F为研究对象，采用改进D-H(Denavit-Hartenberg)法建立机械臂运动学模型，通过逆运动学求解确立机械臂在关节空间的起始位置和目标位置后，在关节空间对机械臂路径进行采样，并在笛卡尔空间对采样结果进行碰撞检测。

如图10所示为RV-2F的三维模型，其有6个自由转动关节，属于一种常见的连杆串联机器人结构。RV-2F关节1的轴线垂直基座朝上；关节2和关节3的轴线水平且平行，距离为a2；关节3和关节4的轴线相互垂直，距离为a3。图11所示为采用改进D-H法建立的RV-2F运动学坐标系。

表1所示为采用改进D-H对RV-2F运动学建模后的尺寸参数，通过测量机械臂可知d1=295 mm，d4=270 mm，d6=70 mm，a2=230 mm，a3=50 mm。

表1 RV-2F机械臂的D-H参数

表2所示为仿真实验时的机械臂运动控制参数，其中起点位置和终点位置是通过对机器臂进行逆运动学求解得到的关节空间内的坐标加权，系数是多次试验得到的较优值。

表2 机械臂运动控制参数表

本次仿真实验采用的计算机处理器为Inter(R) Core(TM) i5-8500 CPU @ 3.00 GHz 3.00 GHz，内存为8 G，实验平台为MATLAB R2016b。

4.1 仿真分析

4.1.1 SAGB_RRT*算法适应性

为验证SAGB_RRT*算法在不同环境下的适应性，选取5种典型环境进行多次仿真实验，如图12所示。环境1是有一个半径为70 mm的障碍物，圆心在空间的坐标为(75,54,395)；环境2有2个半径为45 mm的障碍物，圆心在空间的坐标为(75,14,395)，(75,104,395)；环境3有3个半径为45 mm的障碍物，圆心在空间的坐标为(75,14,395)，(75,104,335)，(75,84,475)；环境4有4个半径为45 mm的障碍物，圆心在空间的坐标为(55,14,395)，(75,104,335)，(75,74,475)，(235,134,365)；环境5有5个半径为45 mm的障碍物，圆心在空间的坐标为(5,14,395)，(75,104,335)，(75,74,475)，(235,134,365)，(0,74,550)。采用SAGB_RRT*算法在这5种复杂环境下为机械臂进行路径规划。可见，不同复杂度环境下，SAGB_RRT*均能快速规划出符合机械臂运动限制条件的避障路径。

4.1.2 SAGB_RRT*算法的有效性

为进一步验证SAGB_RRT*算法的有效性，在4.1.1节环境下，分别采用SAGB_RRT*算法和不同阈值的GB_RRT*算法进行15次仿真规划，结果取平均值。如图13a和图13b所示，在不同环境下，SAGB_RRT*算法比不同固定阈值P的GB_RRT*算法规划得到的路径均更优，路径长度降低约30%，而且在多次仿真实验规划出的路径中，SAGB_RRT*算法比GB_RRT*算法的稳定性更好。如图14c所示，在5种不同的环境中，由于引入栅格法存储、open表存储和自适应调整目标阈值，SAGB_RRT*算法比GB_RRT*算法规划所需的搜索时间更具优势，降低约50%。如图14d所示，在不同环境下的15次仿真实验中，SAGB_RRT*比GB_RRT*所需的搜索时间更稳定。综上所述，相比固定阈值P的GB_RRT*算法，SAGB_RRT*算法对环境具有较强的感知能力，其能根据环境调整随机树扩展的偏向性，保证机械臂在各种复杂的工程环境下以较短的时间规划出最优且最稳定的避障路径。

4.1.3 不同算法对比

在4.1.2节的5种障碍物环境中，分别比较SAGB_RRT*算法与蚁群优化(Ant Colony Optimization, ACO)算法、PRM、APF+RRT混合算法、GB_RRT*算法的规划能力。图14所示为将5种复杂环境中采用不同算法仿真分析15次后得到的结果取平均值进行比较，数据显示SAGB_RRT*算法规划路径所需的平均搜索时间和平均代价均优于其他算法。

如图14a所示，SAGB_RRT*算法在5种环境下均能稳定地用较少的搜索时间规划出路径，其优势相比ACO和PRM尤为明显，主要原因为ACO和PRM在保证采样次数的基础上才能搜索出较优路径，导致其在有限搜索时间内的算法性能不佳。如图14b所示，SAGB_RRT*算法在5种环境下均能稳定地规划出较优的路径,其优势相比APF+RRT尤为明显，主要原因为APF在高维环境下规划时极易陷入局部极值点，RRT将其从局部极值点引出时会“绕路”，导致APF+RRT规划的路径较长。SAGB_RRT*算法也明显优于GB_RRT*，主要原因在于GB_RRT*采用固定的目标偏向阈值，当初始化的目标偏向阈值较高时，虽然可以保证其规划的路径较短，但是却极易因陷入局部搜索而增大搜索时间；当初始化的目标偏向阈值较低时，会因搜索漫无目的而增大路径代价和搜索时间。

4.2 实验验证

为进一步验证SAGB_RRT*路径规划方法的有效性和可行性，通过实验对仿真结果进行验证，如图16所示。图中采用SAGB_RRT*算法为机械臂规划起始位姿到目标位姿的避障路径，将规划所得的机械臂运动路径导入机器人示教器，并设置机械臂的速度比率为2。重复上述操作并进行20次实验，机械臂都能避开障碍物且平均运行用时25.8 s。再采用ACO，PRM，APF+RRT，GB_RRT*进行实验，平均运行时间分别为28.5 s，26.6 s，28.7 s，27.3 s，可见SAGB_RRT*算法所规划路径的平均运行时间小于其他算法。通过实验可知，采用SAGB_RRT*算法对机械臂进行路径规划不但有效，而且所规划出的路径比其他算法更优更短。

5 结束语

本文通过在救灾、采矿、高空装配、检测焊接和行星探测等环境下分析移动机械臂的作业需求，提出在关节空间内采用SAGB_RRT*算法进行路径避障规划，该算法结合RRT*渐进最优思想对GB_RRT*算法进行优化，借助栅格储存数据快速查找相邻节点，并引入open表解决目标偏向扩展带来的重复偏向问题，提出通过open表节点数量变化自适应控制偏向性生长，并利用可变间隔的贪心算法对已规划的路径进行优化，从而在复杂障碍物环境下用较短的搜索时间快速规划出较优的避障路径。仿真实验显示，相比改进前，SAGB_RRT*算法进行规划时所需的平均搜索时间降低了50%，规划的平均路径降低了30%，而且大幅提升了规划的稳定性；相比其他算法，SAGB_RRT*算法能够很好地兼顾搜索时间和路径代价，在进行避障的同时保证规划所需的平均搜索时间和所规划出的平均路径均为最优，因此采用本文所提的SAGB_RRT*算法对移动机械臂进行路径避障规划是有效的。基于SAGB_RRT*算法的路径避障规划方法，能够在较短的搜索时间内规划出较优的避障路径，为移动机械臂在危险环境下进行快速路径规划提供技术支撑。