基于ABAQUS CEL的高速水冲击载荷仿真与试验研究

齐贺阳，田永卫

（航空工业北京长城计量测试技术研究所，北京 100095）

0 引言

水陆两栖飞机在水箱充水过程中［1］，当水与结构冲击时，会造成关键部位及其压力传感器损坏。由于“水锤”效应的影响，使结构表面产生高动态、高幅值压力冲击，超过了压力传感器的量程［2］，从而导致压力传感器受损。因此，在水流冲击结构时产生的水冲力载荷极值，对飞机载荷测量过程中的传感器选型、测试参数配置和结构强度设计等尤为重要。

国内外诸多学者针对高速水流冲击问题进行了深入的研究。Korobkin 等人［3-4］对高速水流冲击问题开展了研究，水流速度在低马赫数范围内，将水流表面的变形忽略不计，但这只适用于高速水流在最初极短的时间内。Ching-Yu 等人［5］对球帽形水柱在不同速度情况下冲击有机玻璃结构的整个过程和高速水流冲击压力在壁面上的分布情况做了研究。Huang 等人［6］通过研究不同假设下高速水流冲击模型，计算冲击压力在壁面上的分布特性，得出壁面上受到的最大水流冲击压力集中在中心处，不同形状的射流端部形成的最大压力不同。Smith［7］通过实验研究了高速水柱射流端部的压力分布，得出最大压力值出现在水柱端部表面的中心处，而非水柱边缘处。孙龙泉等人［8］运用线性波动方程，研究了可压缩冲击流体对于平板前期的压力特性。孙士丽等人［9］基于线性波动方程研究了高速水流冲击壁面的压力空间分布问题。崔雄伟等人［10］搭建了一种新型高速冲击水流的试验系统，测得的高速水流形成的冲击压力满足理论公式，并探究了腔口位置和腔口深度对于水射流形态的影响。目前大多数研究都集中在用不同端部形状的柱状体模拟水流冲击，所得的“水锤”压力相差较大，且水流冲击时间受限于水柱的长度。

本文基于ABAQUS CEL 数值仿真方法对高速水流冲击平板进行模拟分析，将经验公式和试验结果进行对比，并深入探究了水冲击压力的影响因素，验证了该仿真方法的准确性，为水冲击载荷研究提供理论依据。

1 理论模型

1.1 经验公式

当高速水流冲击表面平滑的结构时，初始压力与水锤压力相等［11］，表达式为

式中：P为压力，Pa；ρ为流体密度，kg/m3；v为水流的冲击速度，m/s；c为流体声速，m/s；α系数与水流速度和水流端部形状有关，通常取α=1。

“水锤”压力为冲击面在初始阶段压力的最大值。圆柱形水柱冲击表面光顺的平板结构，初始阶段产生的高压在边界反射波作用下，逐渐地向水流内部传递。若进行持续不断的冲击，压力峰值会快速下降，直到流动达到稳定状态，则冲击压力将接近流体动力学压力，表示为

1.2 有限元分数值仿真背景

采用ABAQUS CEL 数值仿真方法进行高速水冲击分析，其属于ABAQUS 中显式动力分析模块，适用于解决爆炸、冲击等非线性问题。欧拉-拉格朗日耦合分析方法（Coupled Eulerian-Lagrangian analyses，CEL），原理融合了欧拉法和拉格朗日方法的优点。其中欧拉法一般用于计算与流体介质有关的问题，适用于大变形问题。而单元是不变形的，材料在单元中流动，欧拉法可以求解涉及流场以及流场的动力学问题，却不能求解结构的动力学响应。拉格朗日法一般用于描述固体结构，用于小变形问题。材料的边界与单元的边界是一致的，所以拉格朗日法计算问题依赖于网格的精度。比较两种方法的优点，CEL方法在解决大变形冲击、碰撞等问题方面具有明显优势。

图1 CEL基本原理Fig.1 CEL fundamentals

2 基于调节腔内气压的水冲击试验方法

2.1 试验原理

近几年，科研人员对于水冲击试验装置做了大量的研究［12-13］。本文提出的水冲击试验装置是通过气瓶向储水容器中不断充气，改变储水容器的内部压力，以达到通过调节储水容器内的气体压力来控制冲击水流速度的目的。储水容器内充满一定压力的气体，打开喷嘴的阀门，高压气体将储水容器中的水通过水管高速向水管端部外推出，从而形成一段高速冲击水流，如图2所示。

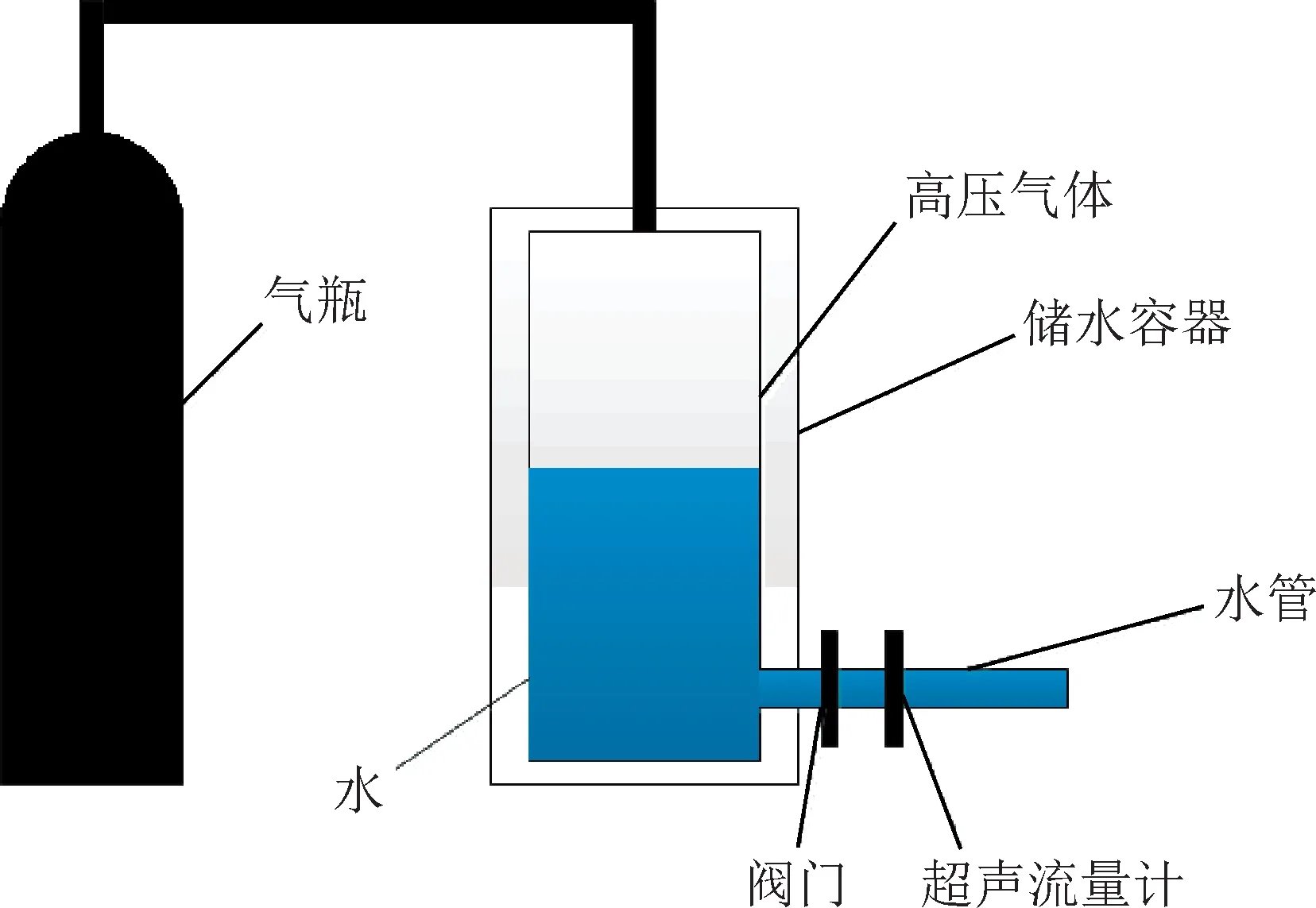
图2 水冲击试验原理示意图Fig.2 Schematic diagram of the principle of water impact experiment

2.2 试验装置与方法

根据上述高速水流生成原理提出的高速水冲击试验装置如图3 所示。水冲击试验装置包含平板、超声流量计、储水容器、压力传感器、高压气瓶和采集设备。在动态压力测试中，正常工况下可采用压力传感器直接进行测量［14-15］。储水容器上安装圆柱形水管及出水阀门，圆柱形水管直径为10 mm，大于安装在平板上敏感元件的尺寸，防止传感器接触不到初始的冲击水流。试验中，水管腔内和储水容器内充满水，避免生成的水流所含空气过多，形成雾化效应，影响测量结果。

图3 水冲击试验装置Fig.3 Water impact test device

水冲击试验步骤：1）布置试验环境，固定试验装置，安装压力传感器和超声流量计；2）在储水容器中加入适量的水，拧紧储水容器上封盖，打开出水阀门使水管内充满水，然后拧紧阀门；3）打开气瓶阀门，向储水容器中充气，压力达到一定时，将高压气瓶的阀门关闭，停止充气；4）打开数据采集系统和超声流量计，确保各装置正常工作；5）打开水管上的出水阀门，开始试验；6）保存试验数据，关闭出水阀门。

在水流速度为10 m/s，水平间距为230 mm 的工况下，通过上述试验可得平板中心压力时间变化曲线，如图4 所示。由图4 可知，曲线在初始阶段出现压力峰值，即“水锤”压力，然后逐渐衰减。且压力传感器测得的压力峰值为1.5 MPa。

图4 平板中心冲击压力变化曲线Fig.4 Variation curve of impact pressure at the center of plate

3 数值计算

3.1 计算模型

在本次计算中，为提高计算效率，将高速水流冲击水箱壁面问题简化为水流冲击平板问题，模型由欧拉体、平板、水管构成。三种模型的具体尺寸、网格信息和材料属性如表1所示。

表1 有限元模型描述Tab.1 Description of finite element model

水管设置在距离平板230 mm 处，平板模型设置在欧拉域中，水管中心与平板中心水平对齐。水管末端表面设置自由入流边界，即水流速度入口，流体速度设置为10 m/s，方向为Z轴正方向，为防止冲击过程中流体流出欧拉域，在欧拉域的各个表面设置相应的边界条件，如图5所示。长方体欧拉域的六个表面中，与X-Y主平面平行的两个表面上设置为vZ=0，vX=vY≠0；与X-Z主平面平行的两个表面上设置为vY=0，vX=vZ≠0；与YZ主平面平行的两个表面上设置为vX=0，vY=vZ≠0。

图5 模型边界条件Fig.5 Model boundary conditions

平板四边和水管末端设置为铰接边界条件，即UX=UY=UZ=0，在模型上设置重力，大小为9.81 m/s2，方向为Y轴负方向。水流从喷嘴到接触平板的时间为0.023 s，为捕获水流冲击初始水锤压力，计算时间设置为0.03 s，时间步增量设置为自动，在计算过程中会根据模型计算调整时间增量大小。在ABAQUS 中建立水流冲击平板模型，如图6所示。

图6 高速水流冲击模型Fig.6 High-speed water impact model

3.2 网格收敛性验证

合适的网格数量可以保证计算结果的准确性，也可以提高计算效率。本次计算模型的网格数量主要集中在欧拉体模型中，通过改变欧拉体全局网格尺寸来改变模型的网格数量，研究了网格数量分别为2.8 万、9.9 万、23 万模型的计算结果，网格具体信息见表2。

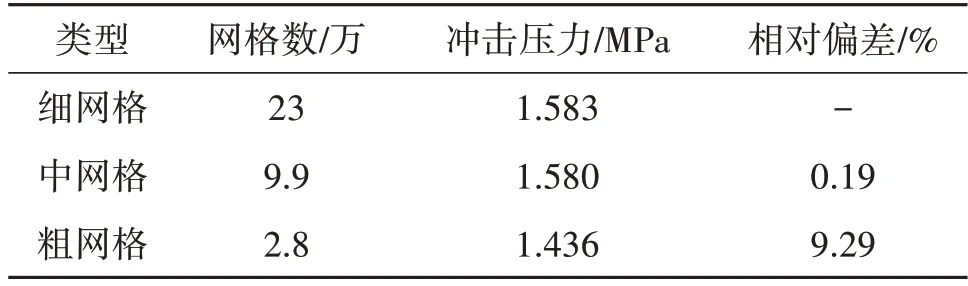
表2 有限元模型描述Tab.2 Description of finite element model

由表2可以看出，以细网格模型的计算结果为标准，粗网格和中网格的计算结果偏差分别为9.29%和0.19%，网格加密程度对结果影响较大。因此，本文采用网格数量为9.9万的模型进行数值计算方可满足精度要求。

3.3 数值验证

图7为某一时刻水流冲击平板的应力云图，可知压力值最大发生在平板中心处，为探究“水锤”压力峰值的变化特性，监测平板中心处单元的冲击压力变化曲线。

图7 平板压力云图Fig.7 Flat plate pressure nephogram

图8 为水平间距为230 mm 时的平板中心处冲击压力随时间变化曲线，冲击压力采集时间间隔为0.00005 s。由图8 可知在水流冲击初始阶段，产生了大于其他时间处的压力峰值，冲击压力峰值大小为1.58 MPa，接近于在相同工况下试验测得的1.5 MPa，验证了仿真计算模型的准确性。但是仿真计算结果和试验结果与“水锤”压力经验公式计算的7.5 MPa相差较大，这是由于水管端部与平板水平间距的差异性造成的。

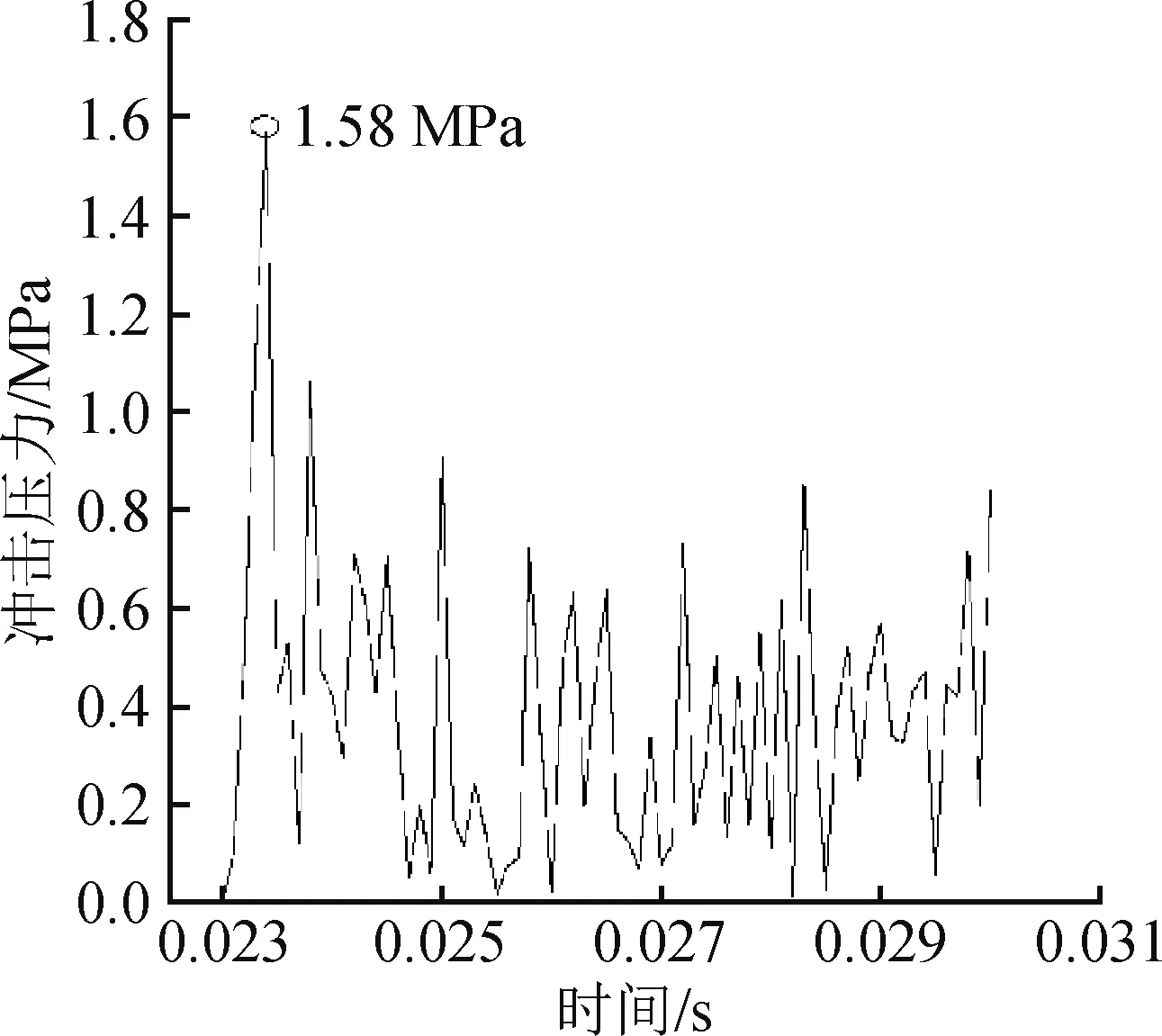
图8 水平间距为230 mm时冲击压力变化曲线Fig.8 Impact pressure variation curve when the horizontal spacing is 230 mm

3.4 冲击压力影响因素特性研究

3.4.1水管端部与平板间距

为进一步探究水管端部与平板的水平间距对于“水锤”压力峰值的影响，分别计算了水平间距为100，50，10 mm 时，在平板中心处受到的“水锤”压力大小变化，计算时间设置略大于水流到达平板的时间，如图9所示。

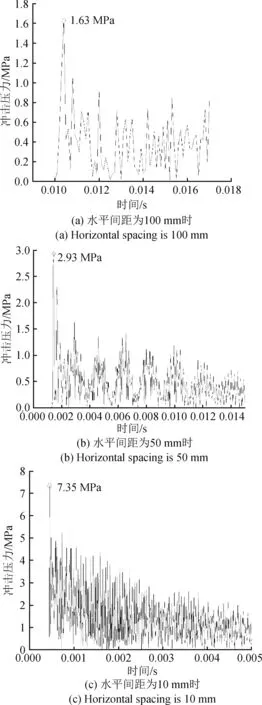
图9 不同水平间距下，冲击压力变化曲线Fig.9 Impact pressure variation curve under different horizontal spacing

由图9可知，随着水管端部与平板之间的距离减小，平板中心受到的水锤压力越来越大，当间距为10 mm时，与“水锤”压力经验公式计算结果相差不大。由于水流受到空气阻力的作用速度逐渐衰减，水流接触到平板时的速度小于在水管出口处的速度，使得冲击压力减小。

为获得水流冲击整个过程的冲击压力从产生“水锤”压力峰值到衰减至平稳状态的变化过程，选取水平间距为10 mm，水流速度为10 m/s 时的冲击压力计算工况。水流从水管端部到达平板时间为0.001 s，计算时间设置为0.055 s，计算时间设置大于“水锤”压力产生时间的50 倍以上，足够捕捉到水流冲击压力达到稳定的变化，计算结果如图10 所示，水锤压力出现之后冲击压力逐渐衰减，直到水流在0.035 s 后趋于平稳，压力值稳定在0.05 MPa 左右，与流体动力学压力计算公式计算所得的0.05 MPa 基本符合，数值仿真与经验公式的计算结果之间的差距较小，验证了数值仿真方法的可行性。

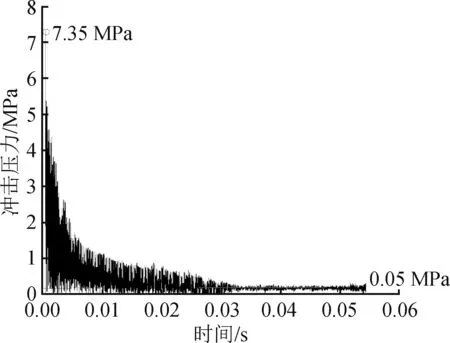
图10 平板中心点处单元的冲击压力随时间变化Fig.10 Variation of impact pressure at the center point of the plate with time

3.4.2水流速度

为进一步了解水流速度对于冲击压力的影响，分别计算水流速度从10～100 m/s 时的冲击压力，水流速度增量为10 m/s，研究冲击压力的变化，并将结果与经验公式计算的结果进行对比。

图11 为平板中心处水锤压力峰值随速度变化曲线，可以看出，通过数值仿真计算的水锤压力峰值与经验公式计算的结果十分接近，基本呈现正比例关系。在速度较低时，仿真计算结果呈现不稳定状态，由于ABAQUS CEL 算法中的接触设置限制，但是仿真计算与经验公式计算结果相差不大，仿真计算具有一定的准确性。

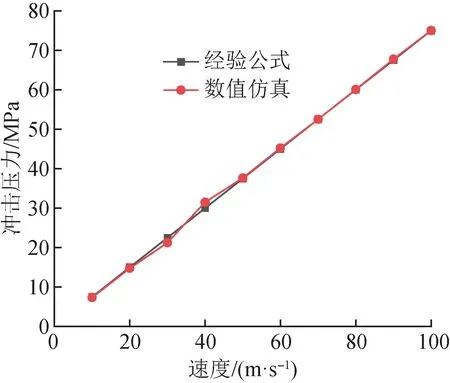
图11 冲击初始阶段水锤压力峰值随速度变化曲线Fig.11 Variation curve of peak water hammer pressure with speed at the initial stage of impact

水流经过初始时刻的“水锤”压力后，冲击压力逐渐衰减，直到稳定接近于流体动力学压力。图12 为在水流稳定状态下平板中心处冲击压力随速度的变化曲线，可以看出数值模拟与经验公式的计算结果十分接近，都呈现二次曲线趋势。

图12 平稳状态下冲击压力随速度变化曲线Fig.12 Variation curve of impact pressure with speed in steady state

综上可知，水流冲击压力受水流速度的影响极大，水流速度越大，初始阶段的“水锤”压力和稳定状态下的冲击压力越大。

4 结论

文章提出了基于ABAQUS CEL 方法计算水流冲击压力，将水流冲击水箱壁面简化为水流与平板之间的冲击。通过开展水流冲击平板仿真计算，计算所得的“水锤”压力峰值与试验测得结果相差不大，验证了数值仿真计算结果的准确性。

相同速度下，试验测得的“水锤”压力和数值模拟结果与理论公式计算结果相差较大。是由水管端部与平板的间距造成的，且间距越大，水流在空气中受到空气阻力衰减地越快。随后通过数值模拟方法计算了三种不同水平间距的工况，验证了水管端部与平板之间水平间距对于水流冲击压力的影响。即水平间距越大，平板受到的冲击压力越小。

为了探究水流速度对于冲击压力的影响，计算了从10～100 m/s 的水锤压力峰值变化和水流平稳状态下的冲击压力，由计算结果可知水流速度的大小对于冲击压力的影响极大，水流速度越大，水流对于平板的冲击压力越大。文章仅对水平间距和水流速度对冲击压力影响进行了研究，水陆两栖飞机汲水过程十分复杂，故将水流冲击进行简化，后续研究应考虑更加复杂的工况和模型，例如不同角度的水流对冲击压力的影响研究、水箱储水的动态特性研究等。