四种测量玻尔兹曼常数的原级温度计研究综述

李小宽，李维，常海涛，蔡静，李新良

（航空工业北京长城计量测试技术研究所，北京 100095）

0 引言

热力学温度是七个基本物理量之一，用来描述物体的冷热程度，是国际上公认的最基本的温度，是一切温度测量的基础。为了测量热力学温度，需要建立一套方法和规则来定义热力学温度的数值，这就形成了热力学温标，符号为T，单位为开尔文（K）。热力学温标先前以实物即水三相点（Triple Point of Water，TPW）温度为基准，水三相点的定义为水的气、液、固三相共存时的温度（273.16 K），1 K 等于水三相点温度值的1/273.16［1］。此定义认为水三相点是一个固定的常量，但实际上，由于水分子氢氧同位素以及杂质的存在，不同区域所取的水的三相点温度存在不一致，并且水的长期存放也会对水的三相点温度产生影响。因此，这种基于实物的温标定义会给温度的测量与传递带来偏差。

2018 年，国际计量大会（CGPM）批准了国际单位制（International System of Units，SI）的修订，将SI 定义从实物的特定性质改为与基本常量直接联系，并从2019 年5 月20 日开始实施［2］。至此，开始用玻尔兹曼常量（k）重新定义开尔文。精确测量玻尔兹曼常量是重新定义开尔文和复现温度的关键，因此温度界开展了关于确定玻尔兹曼常量的大量研究。本文将全面梳理测量玻尔兹曼常量的方法，对原级温度计的定义与分类进行详细阐述，之后从原理、不确定度来源、研究进展等方面对四种原级温度计进行具体介绍，最后对原级温度计未来发展方向进行总结与展望，进而为热力学温度的复现和传递提供借鉴。

1 原级温度计

在温度计量领域，如果描述热力学温度T与其他独立物理量之间关系的方程是明确已知的，并且方程中不包含任何未知或与温度有关的常数，则基于该方程，通过精确测量独立物理量得到热力学温度的测量装置被称为基准温度计。由于基准温度计通过基本物理原理直接复现热力学温度，所以温度测量准确度最高，处于温度计量的源头，也称为原级温度计（Primary Thermometry）［3］。

原级温度计对科学界至关重要：一方面，由于测量得到的是绝对温度，因此可以对其他次级温度计进行量值传递；另一方面，测量结果可以在国际不同计量机构之间进行比对，确保温度单位一致性。

原级温度计的制作是一项复杂且精密的系统工程，由于其门槛较高，目前原级温度计均由国家级计量机构研制。这些国家级计量机构包括美国国家标准技术研究院（NIST）、德国物理技术研究院（PTB）、英国国家物理实验室（NPL）、法国国家计量院（LNE-CNAM）、意大利国家计量院（INRIM）、中国计量科学研究院（NIM）等。

用于测量玻尔兹曼常量的原级温度计如图1所示，根据测量原理可分为以下两类：①基于气体热力学状态方程的原级温度计：声学气体温度计（AGT）、介电常量气体温度计（DCGT）；②基于统计和量化方法的原级温度计：约翰逊噪声温度计（JNT）、多普勒展宽温度计（DBT）。

图1 四种原级温度计原理示意图Fig.1 Schematic diagram of four primary thermometers

1.1 声学气体温度计

声学气体温度计利用共鸣腔精确测量声学共振频率，结合气体声速维里状态方程，计算得出热力学温度。

声音在气体介质中传播时，会引起气体介质压力、密度和温度的变化，但气体的压缩与膨胀过程比气体热传导过程快得多，因此可将声波的传播视为绝热过程。由波动理论，声速u可表示为［4］

式中：S为熵；v为气体比容；ρ为气体密度，ρ=1/v；p为气体压力。

理想气体声速u0通过热力学微分关系式得到

式中：M为气体分子摩尔质量；T为热力学温度；NA为阿伏伽德罗常量；cp为气体定压比热；γ0为理想气体的比热比，对于单原子气体，γ0≡

式（2）为声速与热力学温度的联系式，基于该公式，通过测量声速得到热力学温度的装置被称为基准声学温度计［5］。利用基准声学温度计测量的热力学温度最终溯源到时间和长度，这两个物理量的测量不确定度在国际单位制中是最小的，这也是声学方法测量热力学温度最准确的原因之一。根据式（2），可以通过相对法测量温度，即通过同时测量两种绝热状态下的单原子气体声速之比来导出两种状态下的热力学温度之比，由于参考温度已知（通常选取水三相点温度作为参考温度），可计算得到待测温度。

在水三相点温度下，通过测量声速可以得到玻尔兹曼常量k。因此，声速的测量是测量玻尔兹曼常量的关键。可通过测量腔体内稳定的干涉信号计算得到声速，具体方法包括变程法和定程法两种。变程法的腔体内有两个平行板，分别装有发射端和接收端，接收端通过移动来接收信号。该方法测量误差较大［6］。定程法中的腔体尺寸是固定的，通过调谐声源频率得到声学共振频率，结合特征尺寸得到声速。定程法的测量准确性较高。圆柱形共鸣腔和球形/准球形共鸣腔是定程法中常用的腔体形状［7］。其中，球形/准球形共鸣由于具有较高能量品质因数、弱声学边界层效应，使其在声学信号测量方面更具优势。此外，非理想扰动因素有比较成熟的抑制和修正扰动方法，因此国际上普遍采用该类型腔体，球形与准球形声学共鸣腔如图2所示。

图2 声学共鸣腔[8]Fig.2 Acoustic resonance chambers[8]

利用AGT测定玻尔兹曼常量k时，不确定度来源为气体平均分子质量和共鸣腔尺寸［9］。He，Ar，Kr，Xe 等单原子气体仍包含多种同位素，在气体摩尔质量测量中，需要对气体进行同位素净化，使用质谱仪测量确定平均分子质量，并采取预防措施，避免因水蒸气与污染物带来干扰。利用微波法测量共鸣腔尺寸不但简化了测量流程，还可实时测量共鸣腔尺寸变化，有效提升测量精度。基于微波法测量共鸣腔尺寸的难点在于提高声学共振频率测量精度及信噪比。

从事声学气体温度计研究的主要机构有NIST，NPL，LNE-CNAM，NIM。1988 年，Moldover 等人利用绝对法声学温度计测量玻尔兹曼常量的不确定度为1.8×10-6［10］。之后，NIST，NPL 等机构在水三相点温度下运用球形或准球形定程共鸣器来测定玻尔兹曼常量。2013 年，NPL 使用氩气在半径为62 mm的球体中进行了高精度玻尔兹曼常量测量，相对不确定度为0.71×10-6［11］。2015 年，LNE-CNAM 发布了使用氦气和铜准球体腔测量玻尔兹曼常量的结果，不确定度为1.02×10-6［12］。2017 年，中国计量院采用定程圆柱法测量玻尔兹曼常量，不确定度为2.0×10-6［13］。

1.2 介电常量气体温度计

介电常量气体测温法的基本思想是用介电常量代替气体状态方程中的密度，并通过填充气体电容器的电容变化来测量介电常量。

理想气体的介电常量表达式为

式中：ε和ε0分别为气体的介电常量和真空下介电常量；α0为静电极化率；N为容器中粒子数；V为容器体积。对于理想气体，式（3）可变换为［14］

式中：p为压强。

对于真实气体，必须通过结合状态方程的维里展开和克劳修斯-莫索蒂（Clausius-Mossotti）方程来考虑粒子之间的相互作用。当忽略高阶项和非常小的介电维里系数时，式（4）可变换为［15］

式中：χ为介电极化率，κeff为电容器的有效压缩率，反映了电容器电极在气体压力作用下的变形，并与p具有充分的近似线性关系；Aε为摩尔极化率，Aε=(NAα0)/(3ε0)；R为摩尔气体常量；B和C为第二和第三介电维里系数。

PTB 使用的DCGT 如图3 所示，在等温屏蔽中有两个电容，左边是参考电容C()0，右边是测量电容C(p)。

图3 PTB使用的DCGT示意图[16]Fig.3 Schematic diagram of DCGT used by PTB[16]

充气与未充气时，左右电容的相对变化由式（6）计算

因此，已知的热力学温度T下（通常是水三相点温度），根据[C(p) -C(0)]/C(0)与p关系曲线的多项式拟合可得到Aε/R的值，推导得出玻尔兹曼常量为

利用DCGT 测定玻尔兹曼常量的不确定度来源有：气体压力测量引入的不确定度分量、电容器有效压缩率测量引入的不确定度分量、电容值测量引入的不确定度分量［14］。为实现ε的测量，在电容器中填充压力为7 MPa的氦气然后抽真空，根据电容的相对变化计算得到ε。如此高的气压会引起电容器的形变，导致有效压缩率的测量存在误差，需要采取措施进行避免。压力和电容测量具有很大挑战性，对压力测量、电容器的设计和组装、有效压缩系数的测定、电容桥的灵敏度等有严苛的要求。

2011 年，Bernd 等人［16］建立的介电常量测温装置在水三相点下测量的相对不确定度为9.2×10-6，低温（21～27 K）测量结果为15.9×10-6。通过碳化钨圆柱电容器以及测试手段的提升，Gaiser等人［17］在2013年发表了在水的三相点玻尔兹曼常量k的改进值（k=1.3806509×10-23J·k-1，相对标准不确定度为4.3×10-6），并在2015 年通过优化压力测量将k的不确定度降低到4.0×10-6［15］。近年来，介电常量气体温度计在电容器的设计和组装、有效压缩性的确定、电容桥的灵敏度、数据的散射和评估方面取得了很大进展，2017 年PTB 测得的玻尔兹曼常量的相对不确定度为1.94×10-6［18］。

1.3 约翰逊噪声温度计

约翰逊噪声又称为热噪声，当温度在绝对零度以上时，导体内的载流子随机运动会导致导体两端产生电位起伏。热噪声是导体或器件的固有属性，对材料和机械变化是免疫的。

约翰逊噪声温度计通过测量电阻的白噪声电压得到热力学温度。均方噪声电压与热力学温度通过Nyquist方程联系［19］，即

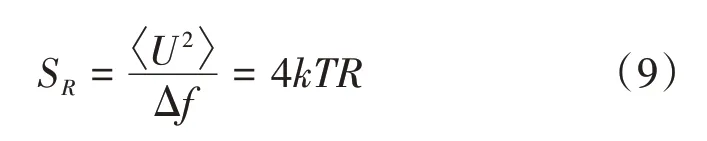
100 Ω 电阻在273.16 K 温度下热噪声功率谱密度值为1.23 nV/Hz1/2，该信号非常弱，必须通过放大器才能测量。然而待探测的信号很容易湮没在背景噪声中，为避免该问题，将处于已知与未知温度的两个噪声信号在同一个放大器通道上进行切换，在相同带宽下通过比值实现测量［20］。该方法存在一个弊端，切换高增益开关的过程会对测量系统稳定性产生影响，故使用数字相关器解决该问题［21］。在数字相关器中，两个通道的信号被数字化，通过软件进行相乘及平均等运算。通过该方式，可以消除放大器和传输线中的干扰噪声，将同一个电阻上的自相关信号保留下来。开关噪声数字相关器原理如图4 所示，其中S 为开关单元；Al 与A2 均为放大器；T为待测温度；R（T）为处于待测温度时的电阻；4 K 为参考温度；e-为电阻中的电子；Vr为量子电压参考源［9］。

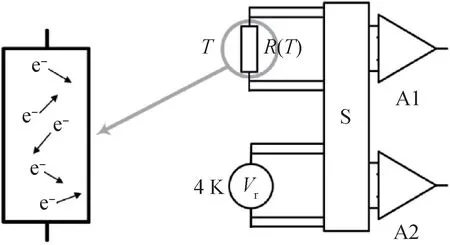
图4 开关噪声数字相关器原理图Fig.4 Schematic diagram of switching noise digital correlator

在实际测量过程中，传统噪声温度计的两个热噪声功率和阻抗无法同时匹配，因此数字相关器的非线性会限制测量水平。随着技术的发展，基于约瑟夫森结的量子电压标准作为赝噪声信号引入到测温中［22］，约瑟夫森结芯片如图5 所示。相较传统噪声测温法，量子电压源可通过编程合成功率并实现阻抗独立输出，减小测量电路非线性引起的系统偏差和测量的相对统计不确定度，并提高测量效率。

图5 NIST制备的约瑟夫森结芯片[8]Fig.5 Josephson junction chip prepared by NIST[8]

在水三相点下，基于量子电压标定的温度计可实现玻尔兹曼常量的测量［23］，具体原理为：利用约瑟夫森结生成的量子电压基准取代参考电阻器，通过相关电学调制技术，形成一个具有可计算功率谱密度的伪随机噪声波形，使用开关数字相关器匹配量子电压噪声的功率SQ与电阻热噪声的功率谱密度SR，使得SQ≈SR，结合式（10）可得出玻尔兹曼常量［24］

式中：SRm为电阻热噪声功率谱密度；SQm为量子电压噪声的功率谱密度，SRm和SQm通过双通道互相关器测量得到；SQ为量子电压噪声功率谱密度；TTPW为水三相点温度；RTPW为三相点下的电阻。k值测量的核心是准确测量SRm/SQm的值［24］。

JNT 测量玻尔兹曼常量的不确定度与以下四个因素有关：①功率谱密度比测量的不确定度；②量子电压噪声源波形的不确定度；③利用水三相点实现开尔文的不确定度；④电阻测量的不确定度。

利用JNT测量玻尔兹曼常量的技术挑战包括以下几个方面［14］：①由于测量的统计性质，测量时间可能需要几个星期，需要确保在整个测试周期内系统均是稳定的；②信号源的阻抗和连线不能完全匹配，以及连接信号源与放大器的两组导线间频率响应的失配，会限制带宽并增加统计不确定性；虽然可以通过功率谱进行校正，但由于模型的不完善，校正过程中统计分量的不确定性会显著增加；③JNT 是纯电学测量，极易受到环境中的电磁干扰，需要对电路供电方式、电磁屏蔽进行优化；④为获得低不确定度的k值，还需保持放大器带宽和增益恒定。

由于具有测量精度高等优势，基于量子电压标定的噪声温度计已成为噪声温度计主流。2011年，NIST 研究人员在水三相点温度下进行基于量子电压标准的玻尔兹曼常量测量，不确定度为12×10-6［25］；通过改进装置，在2017 年获得了5.0×10-6的不确定度［26］。NMIJ 与AIST 联合开发了约翰逊噪声温度计，其测量不确定度为10.22×10-6［27］。2011 年中国计量院开始搭建量子电压标定的噪声温度计系统，在2017 年获得的不确定度为2.7×10-6，是噪声法重新定义开尔文的唯一测量结果［28］。

1.4 多普勒展宽温度计

在气体介质共振频率附近的一个相对狭窄的光谱区域内，以（半）连续的方式调谐激光频率，由探测器记录频率（波长）与光束强度的函数关系，即可得到激光吸收光谱，吸收峰对应给定原子或分子的两个量子态之间跃迁。多普勒展宽是由速度分布导致的光频吸收变化引起的，在光谱上表现为谱线加宽。对于热平衡状态，气体粒子速度分布可通过玻尔兹曼常量与温度联系，根据谱线宽度可计算得出热力学温度，利用上述原理进行测温的方法称为多普勒展宽测温［29］。

可以用电磁波在坐标系中的多普勒频移解释气体分子与探测器相对运动时所发生的气体吸收频率改变。当一个吸收频率为v0的原子或分子以速度s向一个静止的可调谐激光光源移动时，其吸收的光频会发生偏移，即激光频率v′满足式（11）时，可被原子或者分子吸收

对于一定温度下的热平衡低压气体，气体粒子速度分布由Maxwell-Boltzmann 公式描述，与exp成正比例，其中M为粒子质量。转换为高斯吸收曲线，则光谱半高宽与热力学温度存在如式（12）关系［30］

式中：ΔvD为多普勒半高宽（HWHM）；v0为谱线中心频率；c为光速；T为热力学温度。式（12）是多普勒展宽测温的基础。

多普勒展宽测温利用直接吸收法或光腔衰荡法得到吸收光谱，用于多普勒展宽测温的激光光谱装置如图6所示。将测试得到的吸收光谱通过线型拟合提取多普勒宽度，再将多普勒宽度代入式（12），如果已知中心频率和粒子质量，则可得出气体所处的热力学温度。在水三相点下进行测试，可以确定玻尔兹曼常量。

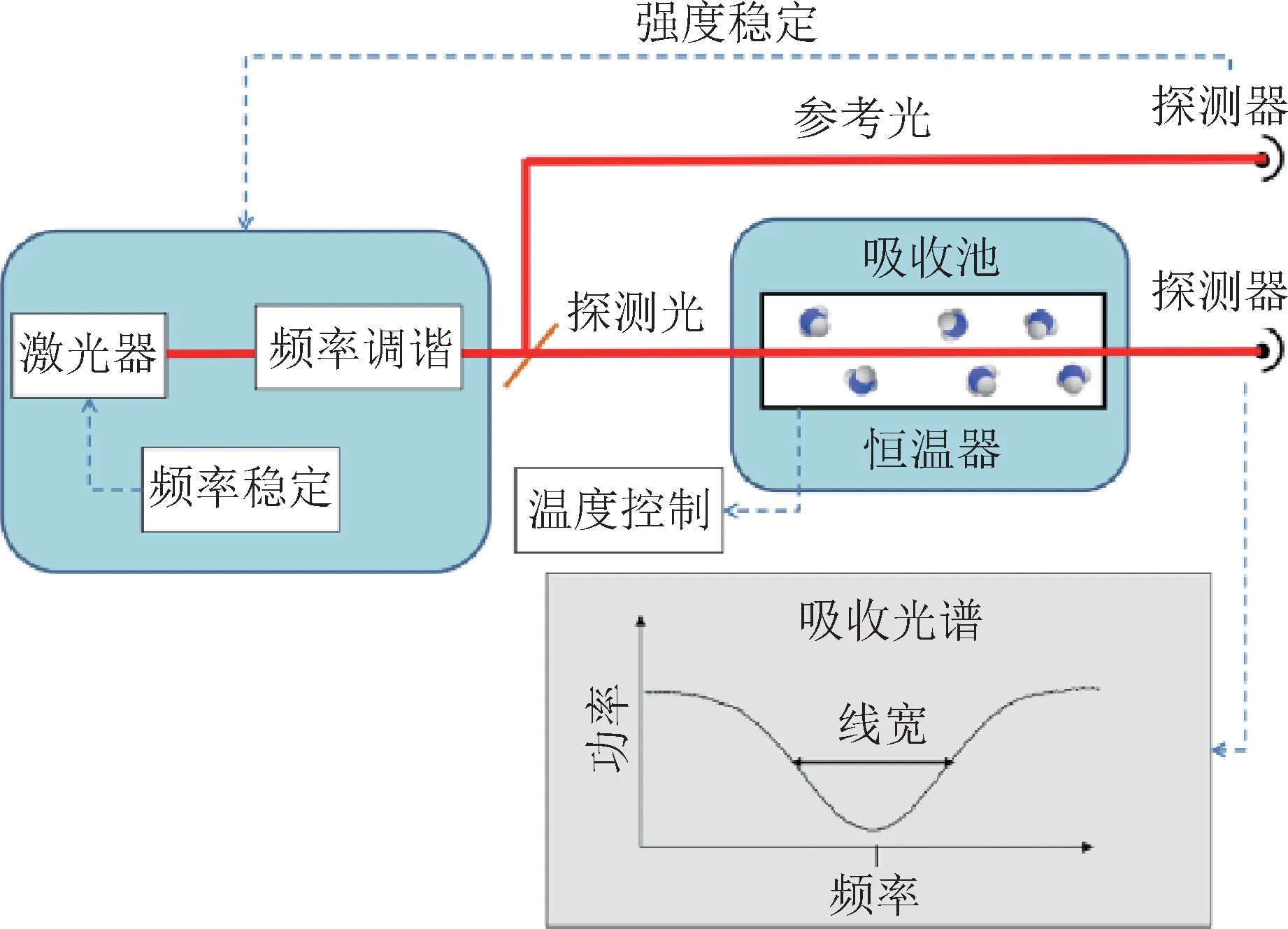
图6 多普勒展宽测温装置示意图[31]Fig.6 Schematic diagram of Doppler broadening temperature measurement device[31]

多普勒展宽测温可以使用标准激光光谱技术进行测量，其优势在于不需要测得绝对辐射量，只需要关注光谱的宽度（多普勒宽度）。多普勒展宽测温将热力学温度与光学频率联系起来，可以利用最近发展起来的光频梳技术提升测量准确度。此外，该方法探测到了一个非常明确的量子态，其结果不依赖于同位素组成。该方法使用的气体压力为0.1～500 Pa，比AGT 和DCGT 实验的压力小一个数量级［32］。因此，多普勒展宽温度计是声学气体温度计和介电常量气体温度计的补充。

影响DBT 测量玻尔兹曼常量的不确定度的主要因素是半高宽拟合。光谱半高宽的拟合与以下几个因素有关：①测温粒子的光谱吸收峰。测温粒子的精细结构与振动模式反映在光谱上为吸收峰，这就要求测温粒子应具有简单可辨且不互相干扰的独立吸收峰，以便提取光谱宽度。②激光频率的稳定性。激光频率的稳定性通过光谱的横坐标体现，频率稳定性越高，则提取的半高宽更符合实际结果。③光谱拟合模型的选取与修正。光谱展宽受多方面影响，包括洛伦兹型均匀展宽、碰撞展宽、二阶多普勒效应、Dicke 压窄效应等。需要充分分析并避免这些因素的影响，因此应选择合适的模型。④整体系统的信噪比。激光功率的波动、探测器的噪声均会引入噪声，在光谱上体现为尖峰，这会对半高宽的拟合带来影响，因此需要提升整体系统的信噪比。

2007 年，法国Daussy 通过拟合14NH3谱线并提取多普勒展宽分量，测量得到的玻尔兹曼常量不确定度为190×10-6［30］，并在2011 年通过优化拟合模型将不确定度降低至6.4×10-6［33］；在2013 年对实验结果进行了修正，并获得了2.3×10-6的B 类不确定度评定结果［31］。2015 年，国内胡水明课题组利用光腔衰荡光谱测量方法测定k，不确定度达到12×10-6［34］。2008 年，意大利那不勒斯大学的Gianfrani 开始进行多普勒展宽测温研究，在2018年利用CO2光谱进行玻尔兹曼常量测量，获得了10×10-6量级的测量不确定度结果［35］。

2 玻尔兹曼常量重定义

过去十几年，初级温度计取得了很大进展，大量研究团队利用原级温度计测量玻尔兹曼常量，促进了k的重新定义。玻尔兹曼常量的调整需要满足以下两个条件［36］：①测量的相对标准不确定度小于1×10-6；②k的确定至少基于两种不同的方法，其中每一种方法至少有一个结果的相对标准不确定度小于3×10-6。这些条件保证了重新定义后，水的三相点温度的最佳估计值仍然保持在273.16 K。

AGT，DCGT 和JNT 均对国际科技数据委员会（CODATA）基本常量工作组重新修订k值做出了贡献（如图7），主要贡献来自AGT，JNT（NIM/NIST-17）和DCGT（PTB-17）各有一个数据被采用［37］。DBT 由于不确定性太大，未被采用。图7中从上到下为按时间测量的玻尔兹曼常量k值，中间绿色区域为±5×10-7，外侧灰色区域为±15×10-7。最下面标红的结果为CODATA 最终值及不确定度。

图7 对定义常量k最终值做出贡献的波尔兹曼常量测得值以及2017年CODATA的值[37]。Fig.7 The measured value of Boltzmann constant contributing to defining the final value of constant k and the value of CODATA in 2017[37].

CODATA 将玻尔兹曼常量k值调整为k=1.38064903（51）×10-23J·K-1，相对标准不确定度为0.37×10-6。用k值定义开尔文无不确定性，保留7 个有效数字的值为1.380649×10-23J·K-1，有效位数的选择使得水的三相点温度仍然保持为273.16 K。

3 总结

声学气体测温法精度最高，是定义玻尔兹曼常量的基石。声学气体温度计利用谐振器内惰性气体的声速与热能的依赖关系来获取热力学温度或玻尔兹曼常量。声学气体测温法实验具有原理简单、气体理论值准确可靠等特点。但AGT 测量热力学温度和玻兹曼常量的研究集中在水的三相点温度附近，在低温和高温区域测量比较困难。此外，AGT 共鸣腔设计复杂、体积大、加工工艺要求较高。目前，AGT 正向扩展低温和高温测量区域方向发展。

气体介电常量温度计通过测量电容器的电容变化来测量介电常数，结合理想气体定律和克劳修斯-莫索蒂方程得到玻尔兹曼常量。该方法有以下特点：气体体积变化与吸附对系统测试没有影响；气体介电常量的测量与电容器内物质的量无关。该方法主要应用于低温区测量，目前正在尝试将氦、氖、氩等气体作为测温介质，以实现更高温区的测量。

噪声测温法为玻尔兹曼常量定义做出了重要贡献。约翰逊噪声温度计根据导体的热噪声波动得出绝对温度，探测电阻在恶劣情况下仍可实现温度精确测量。该测温方法无需进行分度，但存在测量周期长、频率响应失配等问题。近几年量子技术热潮使基于量子电学基准的噪声温度计成为研究热点，量子器件的发展使得基于量子电压标定的噪声温度计测试精度得到很大提升。此外，微电子电路技术的迅速发展使得噪声测温具有很大的改进潜力，有望在极端环境下实现热力学测量。

多普勒展宽测温是一种新型原级测温方法，它将热能与一个绝对频率（即原子或分子共振线中心频率）和一个频率间隔（即谱线多普勒宽度）联系起来，是定义玻尔兹曼常量的重要补充。多普勒展宽测温充分利用了激光吸收光谱分辨力高的特点，测量范围和测量时间适中。多普勒展宽温度计目前正处于初步研究阶段，受限于探测光光谱纯度和拟合模型等因素，其测量不确定度相较传统基准温度计的测量不确定度大很多。在这几种测温方法中，多普勒展宽测温是最有可实现芯片化的测温方法，具备传递开尔文的潜力。

本文回顾了用于测量玻尔兹曼常量的四种原级温度计，详细阐述了原级温度计的定义、测量原理、不确定度来源、研究进展等多方面内容。其中声学温度计、介电常量温度计、约翰逊噪声温度计均对玻尔兹曼常量定义做出了贡献，多普勒展宽测温由于具有较大的不确定性，仅作为额外的补充。用玻尔兹曼常量重新定义开尔文单位摆脱了原定义对实物的依赖，为热力学温度的测量奠定基础，促进了原级温度计精密测量技术开发。在未来，原级温度计有望复现和传递热力学温度，推动温度计量学科进一步发展。