更好理解一边靠墙面积最大的问题
文|沈 勤
用篱笆围菜地,当一边靠墙时,长和宽越接近,面积不一定越大。如何打破学生的思维定势,帮助学生更好地理解一边靠墙时面积最大的数学本质?可以采用以下教学过程。
一、唤醒“周长相等,正方形面积最大”的经验
情境:小明妈妈要在花园里种菜,用12米的篱笆围出一块长方形菜地(整米数),怎样围菜地的面积最大?学生列式解决,集体反馈。唤醒学生已有经验“周长相等,围成正方形时面积最大”。
二、探究“一边靠墙,面积最大”的规律
情境:用12米的篱笆围出一块长方形菜地,一边靠墙(墙足够长),怎样围菜地的面积最大(整米数)?学生猜测,预设学生认为围成正方形时面积最大。借助表格和画图,组织学生进行探究活动(如图1)。
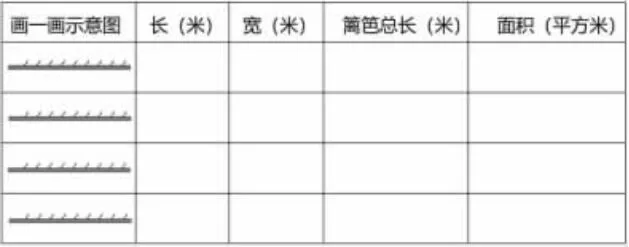
图1
反馈交流,预设学生发现:一边靠墙,围成正方形时面积不是最大的。发现围成长6米、宽3米的长方形时面积最大。追问:长6米,宽3米时,长与宽有什么关系?引导学生发现:长是宽的2倍。
更换篱笆的长度,改为20米和32米(篱笆总长度为4的倍数),当长和宽分别是多少时面积最大?让学生借助画图和表格,通过计算发现仍然当“长是宽的2倍”时,面积最大。
三、明晰“一边靠墙,面积最大”的原理
提出思考:一边靠墙,为什么当长是宽的2倍时,长方形面积最大?以篱笆的长度12米为例进行探究(如图2)。教师提供镜子,学生以四人小组为单位进行探究,观察镜子里外所拼成的图形(如图3),并在组内讨论自己的发现。

图2

图3
借助镜面观察,发现镜子里的三条边和镜子外的三条边可以组成一个周长为24米的长方形。当镜子外的长方形,长是宽的2倍时,镜子里和镜子外正好组成一个正方形。当周长都是24米时,正方形面积最大,镜子外是正方形面积的一半,也是最大的。
教师呈现图4的两种围法,计算其面积,说一说有什么发现?学生再次感悟到只要镜子里和镜子外拼起来是一个正方形,围出的面积就是最大的。
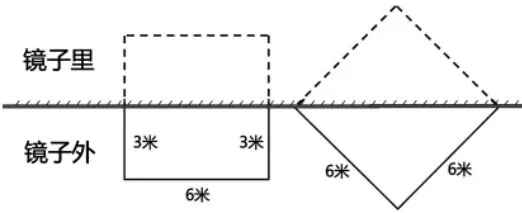
图4
用篱笆围四面和一边靠墙,看似结论不一样,其实是有关联的,都是运用“周长相等,正方形面积最大”这一规律。

