借助模型理解有余数除法的单位名称

文|应诗颖

借助模型能更好地理解有余数除法的单位名称，明确算式中各部分的含义，认识单位名称的重要性，可以安排以下教学活动。

一、分一分

1.阅读问题。问题1：想一想每盘分3个，要分完6个、7个、8个、9个的饺子，分别可以怎么分？

2.分一分。学生尝试用画图的方式表示分的过程，并给这4个结果分分类。学生发现，分6个饺子和9个饺子时是正好分完的，可以分成一类；分7个饺子和8个饺子时是有剩余的，可以分成另一类。

3.算一算。将分8个饺子的过程用算式表达出来，全班分享后整理出不同的表达方法：8÷3=2（盘）……2（个）；8÷3=2（盘）……2；8÷3=2……2。

二、比一比

1．圈一圈。引导学生用不同颜色的笔标识分完的结果，用红色笔圈一圈几盘，用蓝色的笔圈一圈还剩下几个。

2.议一议。学生阅读问题2和问题3并尝试列式计算。

问题2：有8片叶子，每3片可以组成一个三叶草，可以组成几组，还剩几片？

问题3：8朵花，每3朵插1瓶，可以插几瓶，还剩几朵？

计算后四人小组讨论，问题1、2、3，这三个问题的解决过程有什么相同和不同。学生发现，用8片叶子组合成三叶草，可以组合成2组，还剩2片。8朵花插花瓶，可以插2瓶，还剩2朵。它们不仅都可以用同一幅图来表示，并且都可以用算式“8÷3=2……2”计算。但在不同的问题中算式各部分表示的意思却大不相同。

3.选一选。再次观察三个学生的作品。

8÷3=2（盘）……2（个）；8÷3=2（盘）……2；8÷3=2……2。

选一选，哪种表示方式更合适。引导学生发现，标注出正确的单位名称可以进行有效区分。所以“8÷3=2（盘）……2（个）”的方法是最好的。

三、议一议

1.阅读问题。

问题4：把8个饺子平均分给3个人，每人分到2个，还剩2个。

学生列式，得出“8÷3=2（个）……2（个）”

2.对比思考。解决问题1和问题4，算式相同，为什么余数的单位名称一样，但商的单位名称不一样？想一想，怎样讲给大家听，能让大家都听明白。

学生讨论后发现，分完后剩下的物品相同，所以余数的单位相同；分的方法不同，一个是分成2个3，一个是分成3个2，所以商的单位不同，要根据实际情况来选择。

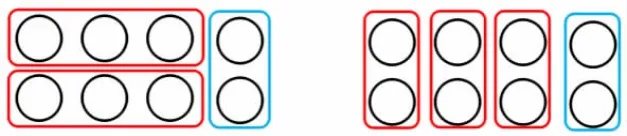
通过“8÷3=2……2”算式的情境变换和结构对比，学生在头脑中顺利建构问题解决模型，提升根据问题情境合理选择单位名称的能力。