污染环境中一类时滞多种群概周期食物链系统全局指数稳定性
郭兴伟,赵凯宏,代云仙
(昆明理工大学 理学院,云南 昆明 650500)
0 引 言
在长期的演化过程中,地球不同地区的生物体形成了相对稳定的生态系统,如海洋生态系统、草原生态系统、森林生态系统和荒漠生态系统等.在生态系统中,根据不同物种之间的相互作用,生态系统可分为捕食型、共生型和竞争型.许多领域的科学家运用各种理论和工具,对物种数量和种群间的相互作用进行广泛而深入的研究,其中以微分方程为工具建立了著名的Lotka-Volterra生态系统模型.该生态系统模型可以动态地描述和刻画生态系统中物种数量和物种间关系随时间的变化.该系统自提出以来,受到了广泛的关注和研究.关于该系统的稳定性、持续性和周期性等动力学行为,已经取得较多的研究成果[1-14].
在捕食系统中普遍存在一类链状捕食结构.该系统的特征是系统中至少有三个物种,第一个是第二个的食物,第二个是第三个的食物,依次类推.在文献[15]中,Rosenzweig 是第一个关注这种链状捕食关系,并对其进行研究的学者.此后,食物链系统受到广泛关注和深入研究,一些相关研究成果可参见文献[16-21].由于不健康的工农业生产,如污水排放、过量使用杀虫剂等行为,使得许多生态系统受到污染,变得越来越脆弱.因此,为了保护生态系统的健康发展,已有学者开始研究毒物对种群的影响[22-28].另外,捕食者捕食食饵后并不能瞬时增加其种群数量,而是要过一段时间后才会显示效果,这种现象就是时间延迟效应.在自然界中延迟效应是普遍存在且不可避免的,因此,在微分方程生态系统模型中加入时间延迟项是很有必要的.
受上述讨论的启发,本文考虑了如下污染环境中一类变时滞n种群食物链系统:

(1)
其中:r1(t)>0表示固有出生率,xj(t)(j=1,2,…,n)代表第j个物种的人口密度,dj(t)>0(j=2,3,…,n)表示第j个捕食者的死亡率,pj(t)(j=1,2,…,n)表示第j个物种包含毒物的平均浓度,ajj(t)>0(j=1,2,…,n)表示第j个物种的种内竞争率,aj,j+1(t)>0(j=1,2,…,n-1)表示第j+1个物种对第j个物种的捕食率,aj,j-1(t)>0(j=2,3,…,n)表示第j个物种捕食第j-1个物种后的转换率,τij(t)>0是时变延迟.假设r1(t)、dj(t)、pj(t)、aij(t)和τij(t),(i,j=1,2,…,n)都是连续的概周期函数.
1 准备工作
定义1[29]设函数u(t):→是连续的.如果对∀ε>0,∃l(ε)>0,对任何长度为l(ε)的区间I,∃δ=δ(ε)∈I使得|u(t+δ)-u(t)|<ε,∀t∈,那么u(t)被称为是上的概周期函数.为方便起见,用AP()表示实数上全体实值概周期函数组成的函数集合.
对任何f∈AP(),定义函数f的Fourier指数和模分别为:
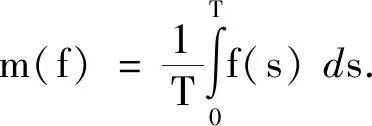
引理 1[5]假设u(t)∈AP()∩C1(,),则u(t)满足下面四种情况之一:
(i) 存在ξ,η∈使得和此情况下有
(ii) 不存在ξ,η∈使得和此情况下,对任何ε>0,存在两个点ξ,η∈使得
(iii) 存在ξ∈使得不存在η∈使得此情况下并且对任何ε>0都存在η∈使得
(vi) 存在η∈使得不存在ξ∈使得此情况下并且对任何ε>0都存在ξ∈使得

(H1)r1(t),dj(t),pj(t),aij(t),τij(t)(i,j=1,2,…,n)都是正的连续概周期函数.
2 概周期正解的存在性

(a) 对每个λ∈(0,1),方程Lx=λN(x)的解x满足x∉∂Ω∩Dom(L);
(b) 对每个x∈∂Ω∩Ker(L)有QN(x)x≠0;
(c) deg(JDN(x),Ω∩Ker(L),0)≠0.

作代换xj(t)=eyi(t)(j=1,2,…,n),则系统(1)变为:
(2)
V1={y=(y1,y2,…,yn)T:yj∈AP(满足
V2={y≡(c1,c2,…,cn)∈n},F1(t)=r1(t)-p1(t)-a11(t)ey1(t)-a12(t)ey2(t-τ12(t)),
Fn(t)=-dn(t)-pn(t)+an,n-1(t)eyn-1(t-τn,n-1(t))-ann(t)eyn(t),
Fj(t)=-dj(t)-pj(t)+aj,j-1(t)eyj-1(t-τj,j-1(t))-ajj(t)eyj(0)-aj,j+1(t)eyj+1(t-τj,j+1(t)),
β是一给定常数.取X=Z=V1⊕V2,对任何y=(y1,y2,…,yn)T∈X=Z,定义范数为:
(3)
应用文献[31]中的方法和技巧容易证明下面的引理.这里只陈述结论,省略具体证明过程.
引理3X=Z在(3)定义的范数下是Banach空间.

引理5设N:X×(0,1)→Z,N(y) = (G1y,G2y,…,Gny)T,其中:
G1y=r1(t)-p1(t)-a11(t)ey1(t)-a12(t)ey2(t-τ12≥(t)),
Gny=dn(t)-pn(t)-an,n-1(t)eyn-1(t-τn,n-1(t))-ann(t)eyn(t),
Gjy=dj(t)-pj(t)-aj,j-1(t)eyj-1(t-τj,j-1(t))-ajj(t)eyj(t)-aj,j+1eyj+1(t-τj,j+1(t)),j=2,3,…,n-1.
定义投影算子:
P:X→Z,Py=(m(y1),m(y2),…,m(yn))T,
Q:Z→Z,Qy=(m[y1],m[y2],…,m[yn])T.

定理1如果条件(H1)和(H2)成立,那么系统(1)至少有一个正的概周期解.
证明考虑算子方程Ly=λN(y),λ∈(0,1),即:
(4)

(5)
一方面,根据式(5)的第一个方程可得:
上式可推出:
(6)
由(5)的剩余两个方程和递推法可得:
上式可推出:
(7)
另一方面,由(5)的第一个方程也可以得出:
上式可推出:
(8)
对(5)的第二个方程应用递推法可得到:
由此解出:
(9)
由(5)的最后一个方程得到:
上式解得:
(10)
结合(6)~(10)可得:
(11)
类似讨论可得:
(12)
由(11)和(12)得:

(13)
因为Ker(L)=lm(Q),所以取J=I.通过直接计算可得

3 全局指数稳定性
定理2如果条件(H1)~(H4)成立,那么系统(1)存在唯一的全局指数稳定的概周期正解.

(14)
由V(t)的定义可得V(0)<+∞.应用条件(H3),进行直接计算可得:
(15)
此外,由条件(H4)可知存在一个常数μ>0使得:
(16)
由(15)和(16)可得:
(17)
在式(17)两端积分可得:
(18)
上式蕴含着:
(19)
(20)

(21)
由式(20)可知,对任何足够小的ε>0,存在T>0使得对t>T都有:
(22)
由式(22)和微分中值定理可得:
(23)
(24)

(25)
构造Lyapunov泛函:
(26)
由式(22)-式(26)可得:
(27)
(27)蕴含着:
(28)
由(28)可得:

在上面的不等式中令ε→0+,有:
(29)

4 结 论
食物链型捕食生态系统是自然界中普遍存在的一种生态现象.本文研究了具有时变延迟的一类多物种食物链系统,获得了系统概周期正解存在的一些充分条件.同时,通过构造恰当的李雅普诺夫泛函建立了系统的全局指数稳定性,从指数稳定性成立的条件中可以看出延迟的重要影响.研究结果为具有食物链型捕食生态系统的研究、开发和保护提供了一些理论参考,所使用的数学理论和方法对其他数学模型的研究也具有一定的借鉴作用.

