轨道车辆铝合金车体结构惯性参数识别方法

刘金安，庞会文，翁建生

(1. 中车长春轨道客车股份有限公司 基础研发部，吉林 长春 130062；2. 南京航空航天大学 能源与动力学院车辆工程系，江苏 南京 210016)

轨道车辆运行稳定性、平稳性和安全性等动力学性能完全是由轨道车辆自身动力学参数所决定的，其中轨道车辆整备车体结构惯性参数是动力学性能优化分析必不可少的参数。由于轨道车辆整备车体是长宽比大、质量和体积庞大的对称结构，且惯性参数张量9个参数相差几个数量级，给惯性参数识别带来了相当大的困难。如何针对车体的结构特点选择合适的测试方法识别其惯性参数是一个工程难点问题。在工程应用中，转动惯量的测试方法通常分为3类：第一，应用物理摆方法，例如利用三线摆和扭振平台方法测量6个不同姿态的振动周期，根据振动周期与某一姿态的转动惯量关系，计算主惯量参数和质心参考坐标系下的惯性张量[1-3]。对于轨道车辆车体这样的大型结构，搭建摆和台架成本高，在工程中很难实现不同姿态的控制；第二，应用多刚体动力学方法，建立多刚体动力学方程，测试外在激励下刚体上相应点的角速度和作用力，通过多刚体动力学方程识别转动惯量[4-5]。这种方法需要大量的角速度、力传感器和复杂的激励系统，台架成本高；第三，应用振动方法，将测试对象安装在弹性元件上，通过激振方法测试频响函数，进行结构件的转动惯量识别。振动方法又分为质量线法、刚体模态法[6]、频响函数逼近法[7]等。其中质量线法在汽车、飞机等领域的转动惯量测试中已有大量成功的范例。通常铝合金车体结构作为整备车体的主体结构，在轨道车辆设计生产过程中具备完整的三维实体数字模型，在材料特性准确的情况下，通过CAD软件也能计算出相对准确的惯性参数。对比CAD三维实体数字模型数值计算结果，分析模态试验质量线法识别轨道车辆车体结构惯性参数产生误差的原因，研究该方法的可行性和准确性对于利用模态试验质量线法进一步识别轨道车辆铝合金整备车体质心和惯性参数具有重大意义。

1 模态试验质量线法惯性参数和质心坐标识别原理

模态试验质量线法惯性参数识别原理是基于车体结构在弹簧支承下振动系统的频响函数测试，运用质量线法识别Z向质心和相对质心的转动惯量。

图1所示的单自由度振动系统，其振动方程为：

(1)

经过时域向频域傅里叶变换，加速度频响函数为：

(2)

式中：m0——质点的质量；

c——阻尼器的阻尼；

k——弹簧的刚度；

x(t)——质点离开平衡位置的位移；

f0(t)——作用在质点上的激振力；

j——虚数单位；

ω——角频率；

x(ω)——响应输出的傅里叶变换；

F(ω)——力(输入)的傅里叶变换。

图1 单自由度振动系统

图2 单自由度加速度频响函数曲线

对于轨道车辆铝合金车体结构，如图3所示有6个自由度，u={xyzαβγ}T。试验坐标(全局坐标)原点为o，车体一端x向为零点，地板平面作为z向零点，y向零点是车体对称中心面。

图3 轨道车辆铝合金车体结构振动系统模型坐标体系

刚体原点运动的线性振动方程为：

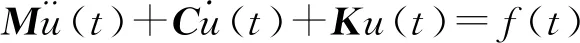
(3)

式中：M——轨道车辆铝合金车体结构刚体质量矩阵；

K——模态试验支承弹簧刚度矩阵；

C——模态试验支承阻尼矩阵；

u(t)——位移响应；

f(t)——广义激励力。

轨道车辆铝合金车体结构刚体质量矩阵M为：

式中：m——轨道车辆铝合金车体结构质量；

(xG，yG，zG)——轨道车辆铝合金车体结构质心坐标。

相对试验坐标原点的惯性矩阵Io为：

相对质心惯性矩阵Ic为：

惯性矩阵Io与Ic各元素之间的关系为：

由惯性积对称性可知：

I12=I21=Ixy-m(xG·yG)

I13=I31=Ixz-m(zG·xG)

I32=I23=Izy-m(zG·yG)

设在试验坐标系中，质心的位置为(xG,yG,zG)，刚体运动的加速度和角加速度矢量为：

作用在刚体上的力和力矩矢量为：

在试验过程中，力锤激振力和测点加速度是局部坐标系，通过坐标变换得到作用原点上的作用力、力矩和6个运动加速度矢量，如下式：

(4)

式中：(xPi,yPi,zPi)——测试传感器在试验坐标系中的坐标。

(5)

式中：(xEi,yEi,zEi)——激振点在试验坐标系中的坐标。

式(3)在频域表达式为：

(-ω2M+jωC+K)u(ω)=F(ω)

(6)

加速度频响函数为：

(7)

类似于单自由度系统，加速度频响曲线的高频段(系统激励频率远大于刚体模态固有频率)也存在质量线。在质量线段：

(8)

在某一激励频率下，将式(8)经过转换可得到关于物理参数的代数方程：

(9)

式中：B—— 加速度响应矩阵；

Φ——转动惯量参数矩阵；

F——作用力矩阵。

在质量线范围内对于每一谱线，由式(9)只能得到存在9个未知数、6个等式的超定方程组，因此选取多个谱线建立等式，可得9个以上的线性方程组，运用最小二乘法可得除质量以外的质心坐标和转动惯量矩阵9个物理参数，如下式：

(10)

(11)

求出相对试验坐标系的转动惯量矩阵参数后，运用坐标系之间转动惯量计算公式可得到质心坐标系转动惯量参数和主惯性矩。

对于轨道车辆铝合金车体结构，在弹簧弹性支承下，除去刚体模态外还存在弹性模态。在弹性模态与刚体模态之间，加速度频响函数有一段直线，将其定义为质量线，如图4所示。

图4 加速度频响函数

因此，最低弹性模态与最高刚体模态频率之比大于一定数值时，可以忽略弹性模态的影响。从以上质量线原理可知，若要提高物理参数识别精度，刚体模态频率要远远小于弹性模态频率。另外，加速度频响函数的测试精度决定物理参数识别精度。

2 模态试验

2.1 试验测试系统

试验测试系统由数据采集系统、加速度传感器和激振设备组成，主要试验仪器如表1所示。

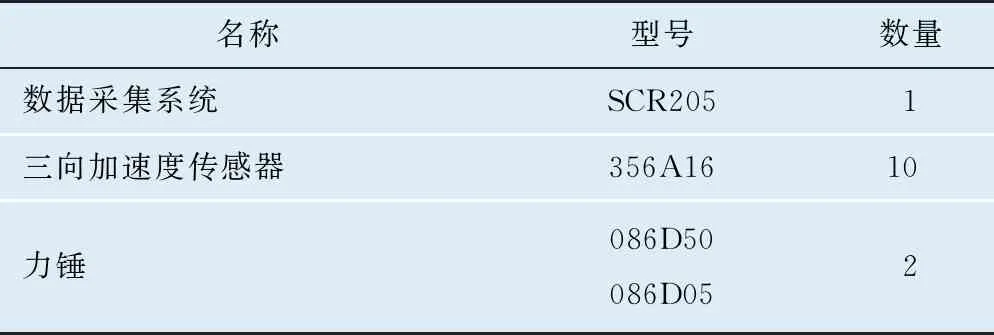
表1 模态试验主要试验仪器

2.2 模态试验方法

根据质量线方法，被试车体支承弹簧的选取原则是车体在弹簧支承下6个刚体模态的固有频率要远远小于车体的一阶弹性模态频率。由于车体质量大，形状为长条形，不能实现在3个方向完全自由悬吊，故本试验采用失气空气弹簧和圆圈形橡胶弹簧串联支承方式来进行试验。为了保证安全，在4个架车点布置架车机，架车机悬臂与车体之间保留3 mm间隙，如图5所示。

图5 失气空气弹簧和圆圈形橡胶弹簧串联支承方式

2.3 试验设置

用力锤激励车体，重复数次测试，通过相干函数和频响函数进行检验。为了提高频响函数测试精度，一般不少于10次重复激励。模态试验的试验参数设置如表2所示。

表2 模态试验的试验参数设置

2.4 模态试验注意事项

轨道车辆铝合金车体结构物理参数识别试验加速度频响函数激励点和响应点布置的原则如下：

(1) 应在局部刚度较大的位置选取激励点和响应点，以防止局部弹性变形影响测试结果；

(2) 激励点位置的选择应避开支承点和结构模态振型节点，响应点的选择主要考虑其能反映结构的主要轮廓；

(3) 激励点和响应点不应布置在同一平面内，更不宜分布在同一条直线上。

本试验针对轨道车辆铝合金车体结构的特点选择相应的激励点和响应点，如图6所示，a和b为响应点，f为激励点。

图6 模态试验的响应点和激励点

2.5 数据处理及计算结果

模态振型分析发现车体6个刚体模态比较纯净，表明失气空气弹簧和圆圈形橡胶弹簧串联支承轨道车辆铝合金车体结构刚体模态没有其他输入。橡胶弹簧支承试验的综合频响函数如图7所示，刚体模态最高频率为11.86 Hz，侧墙局部弹性一阶弹性模态频率为13.87 Hz。刚体模态与弹性模态接近，表明失气空气弹簧和圆圈形橡胶弹簧串联支承产生的刚体模态偏高。

图7 橡胶弹簧支承试验的综合频响函数

轨道车辆铝合金车体结构惯性参数试验识别结果如表3所示。

表3 轨道车辆铝合金车体结构惯性参数试验识别结果

3 车体CAD惯性参数计算和试验结果对比分析

利用三维实体造型软件获取惯性参数，是随着三维造型软件的发展而产生并发展起来的一种理论方法，很多三维实体造型软件和有限元计算软件均包含此功能，如CATIA、Pro/E、UG、ANSYS、ADINA等。对于材料特性参数准确且结构简单的规则刚体，该方法可获取精确的惯性参数。根据轨道车辆铝合金车体结构CAD模型，运用CATIA计算转动惯量方法计算车体的转动惯量如图8所示。根据不同坐标系之间转动惯量转换方法计算得出质心坐标系转动惯量和主惯性矩。假定铝合金的密度为2 710 kg/m3，CAD计算结果见表4。

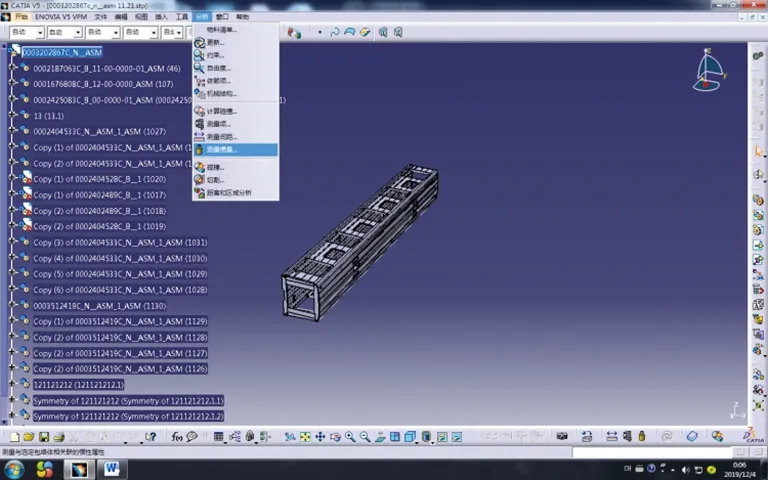
图8 轨道车辆铝合金车体结构CAD模型

表4 轨道车辆铝合金车体结构惯性参数CAD计算结果

从CAD计算结果可知，由于车体结构是长宽比大，x方向主惯性矩与y、z方向主惯性矩比较，相差1个数量级。在惯性张量的非对角元素惯性积接近0，这对于惯性参数识别是一大难点。质心在y方向也接近0，这对于y方向质心的识别精度也是一个挑战。

表5为轨道车辆铝合金车体结构惯性参数试验识别结果和CAD计算结果对比分析情况，由表5可以发现，主惯性参数Iyy、Izz和质心坐标zG的识别精度在可接受范围。对于其余参数的识别差别分析如下：

(1) 在失气空气弹簧和圆圈形橡胶弹簧串联支承条件下，刚体模态与弹性模态没有完全分离，弹性模态的影响大。另外，车体宽度方向相对长度小，在测试过程中，y方向支承距离小，绕x方向的加速度相对y、z方向要小1个数量级，将加速度转换为质心角加速度过程中产生的误差大。因此需要重新设计弹性支承刚度和y向支承距离；

(2) CAD模型和轨道车辆铝合金车体结构实物存在差别，经分析该差别主要是由于车体在制造过程中焊接所导致，需要对CAD模型重新进行校准；

(3) 对于对称性结构，质心y方向坐标和惯性张量的非对角元素惯性积理论计算接近0，CAD计算的惯性积相对主惯性矩小5个数量级。以CAD分析作为参考计算差别，当产生一点测试误差时会产生无穷大的误差。因此，在后期的测试过程中，可通过破坏对称性、加偏置质量消除对称状态。

表5 试验识别结果与CAD计算结果对比分析 %

4 结束语

本文探讨了应用模态试验方法得出振动频响函数，运用质量线法识别轨道车辆铝合金车体结构惯性参数的方法。根据质量线法理论，识别了轨道车辆铝合金车体结构的惯性参数。试验识别结果表明，基于频响函数测试的质量线法对车体结构的质量m、质心x轴坐标xG、主转动惯量Iyy和Izz具有较高的识别精度。对比试验识别结果与CAD计算结果，给出了对比差别的原因和试验设计改进的建议方案。

针对轨道车辆铝合金车体结构的特殊性，合理设计模态测试支承的刚度和附加偏置质量，可以进一步提高其他惯性参数和质心坐标的识别精度。由于该方法易于操作，需要的设备简单，在轨道车辆整备车体的测试中必然会有更广泛的应用。