一种新的全局排序高维多目标优化算法

刘仁云, 张美娜, 姚亦飞, 于繁华

(1. 长春师范大学 数学学院, 长春 130032； 2. 长春师范大学 计算机科学与技术学院, 长春 130032；3. 北华大学 计算机科学技术学院, 吉林 吉林 132013)

多目标最优化问题(multi-objective optimization problems, MOPs)在工程实践和日常生活中应用广泛. 多目标优化问题需要同时对多个目标函数进行优化, 而一个目标的性能提高通常会导致其他目标的性能下降, 使得对这类算法的求解变得更困难. 目前, 已有许多应用广泛的多目标进化算法(multi-objective evolutionary algorithms, MOEAs), 例如： 一个快速精英机制的多目标遗传算法(a fast and elitist multiobjective genetic algorithm, NSGA-Ⅱ)[1], Pareto进化算法的改进(improving the strength Pareto evolutionary algorithm, SPEA2)[2]等算法, 但这些算法在求解高维多目标优化问题时性能显著下降. 针对高维多目标优化求解问题目前已有许多方法, 主要分为Pareto支配和非Pareto支配方法. Pareto支配方法, 如ε-Pareto支配[3]、 网格排序[4]、α-支配[5]等, 该类方法的缺点是需要根据主观偏好给出相应的准则, 随着目标个数的增加, 在一定程度上增大了非支配个体的选择压力, 不能从根本上解决选择压力退化的问题. 非Pareto支配方法, 如平均等级排序(average ranking, AR)[6]、 全局排序(global ranking, GR)[7]等, 这些方法能获得较好的解集收敛性, 但没有很好地解决解集分布性. 针对非Pareto支配存在的问题, 本文提出一种新的基于全局排序求解高维多目标优化问题算法(a novel global sorting many-objective optimization algorithm, NGR-MOEA), 该算法不仅具有良好的收敛性, 而且解决了解集分布不均匀的问题.

1 高维多目标优化问题描述

多目标优化问题定义为

(1)

其中Ω是决策(变量)空间,F:Ω→m由m个真实的目标函数组成, 且m称为目标空间, 可实现的目标集定义为集合{F(x)|x∈Ω}.

定义1(Pareto支配)[7]假设有两个解p和q, 如果满足下列条件:

(2)

则称pPareto支配q, 其中m是目标个数.

定义2(Pareto最优解集)[7]对于问题(1)的一个解x*∈Ω, 如果不存在x∈Ω, 使得xx*, 则x*为该问题的Pareto最优解. 由所有Pareto最优解构成的集合, 称为Pareto最优解集(Pareto optimal solution set, PS).

定义3(Pareto前沿)[7]Pareto最优解集在目标空间形成的曲面, 称为Pareto前沿(Pareto optimal front, PF).

2 新的全局排序高维多目标进化算法

MOEAs的目的是将非支配目标向量较好地收敛到PF, 同时生成的向量在PF上有良好的分布性. 为提高MOEAs在高维多目标优化问题上的收敛性和分布性, 本文提出一种新的基于全局排序的高维多目标进化算法(NGR-MODE).

2.1 个体目标适应度计算策略

文献[7]给出了一种个体目标适应度计算方法, 该方法对两两个体在目标空间中进行比较, 进而确定个体适应度. 定义种群POP中每个个体Xi的全局排序值GR(Xi)等于该个体在所有目标上与种群中所有其他个体相应目标值的差值之和, 计算公式为

(3)

其中个体Xj为种群POP中不同于Xi的任意个体,m∈[1,M]为目标维数,fm为个体在第m个目标上的归一化函数值.

2.2 灰色关联分析

灰色关联分析[8]是指对一个系统发展变化态势的定量描述和比较方法, 其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度判断其联系是否紧密, 其反映了曲线间的关联程度.操作步骤如下：

1) 确定反映系统行为特征的母序列及影响系统行为的子序列；

2) 对数据进行无量纲化处理(由于系统中各因子列的数据可能存在维数上的差异, 比较不方便或难以得出正确的结论, 因此灰色关联度分析一般需要对数据进行无量纲处理, 即归一化处理), 计算公式为

(4)

3) 计算关联系数

(5)

4) 计算灰色关联度

(6)

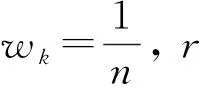
5) 评价分析, 根据灰色关联度对评价对象进行排序, 关联度越高, 评价结果越好.

2.3 新的全局排序方法策略

目前, 大多数MOEAs的适应值评价方法仅计算个体在每个目标上的函数值, 再通过各类支配排序方法比较其优劣. 在高维多目标优化问题中, 许多支配排序方法被改进, 改进后的支配排序方法虽能在一定程度上增强选择压力, 提升收敛性能, 但解集的分布性欠佳. 有些算法在充分考虑分布性后收敛性得不到满足. 基于此, 本文将个体目标适应度计算策略与灰色关联分析相结合, 设计一种新的精英选择策略. 对于种群中个体Xi, 假设其在所有目标函数上与种群中其他个体相应目标值的差值之和为GR(Xi), 与种群中其他个体相应目标值的灰色关联度为GRA(Xi), 则其全局适应度值为

fitness(Xi)=w1×GR(Xi)-w2×GRA(Xi),

(7)

其中w1和w2为在[0,1]内取值的权重系数, 用于协调收敛性及分布性的权重, 本文取值分别为1.5和0.5.

该精英选择策略由两部分组成： 一是通过个体目标适应度计算策略直接给出种群中每个个体的优劣程度； 二是在每次迭代中选取函数值最小目标组成理想点序列(母序列), 每个个体的目标函数值组成比较序列(子序列). 通过灰色关联分析计算母序列与子序列的关联度, 增强灰色关联度高的子序列所对应个体被选择的概率. 通过确定母序列和若干子序列的几何形状相似程度判断其联系是否紧密, 紧密程度越高其分布越接近理想点序列, 反之亦然, 以此保证PF上具有良好的分布性.

2.4 算法流程

本文以遗传算法(genetic algorithm, GA)为基底, 分别将全局排序(global ranking, GR)、 灰色关联分析(grey relation analysis, GRA)引入遗传算法的框架中.

算法1NGR-MOEA.

输入: 目标个数M, 种群大小N, 最大迭代次数MaxGen; /*输入目标个数、 种群大小、 最大迭代次数*/

输出: 新种群; /*输出新的种群*/

步骤:

1)P=Ø,i=1;

2)P=Randominitiate(P);/*随机初始化种群*/

4)Q=MatingSelection(P); /*交配选择*/

5)Q=Variation(Q); /*交叉变异*/

6)R=P∪Q; /*将父代种群与子种群混合*/

7) ComputeFunctionValue(R)；

8) ComputeGlobalsortingValue(R)； /*计算每个解的全局排序值*/

9) ComputeGreyRelationDegree(R)； /*计算每个解的灰色关联度*/

10) ComputeFitnessValue

fori=1∶size(newpopulation,1)

FitnessValue(i)=w1×GR(Xi)-w2×GRA(Xi)

end

[B,I]=sort(FitnessValue)； /*对每个解的适应度评估值进行排序*/

11) end while.

NGR-MOEA随机产生初始种群P, 使|P|=N.每次迭代, NGR-MOEA应用一些遗传运算符, 如在步骤4),5)的交配选择[9]和交叉变异[10], 产生子种群Q.将P和Q混合成临时种群R=Q∪P, 即|R|=2N.最后, 利用步骤7)～10)的环境选择对混合种群进行排序, 并选择精英解进入下一代.

在环境选择中, 首先在步骤7)计算每个解的目标函数值; 然后利用式(4)目标函数进行归一化处理, 并利用式(3)在步骤8)计算每个解的全局排序值, 利用式(6)在步骤9)计算每个解的灰色关联度; 最后将全局排序值与灰色关联度进行混合设计新的适应度函数, 计算每个解的适应度函数值, 选择精英个体, 直到达到终止条件, 算法停止.

3 仿真实验结果与讨论

本文实验使用反世代距离评价指标(inverted generational distance, IGD)[11]和空间评测方法(spacing metric, SM)[12]两个质量指标对算法进行性能评估. 实验中, 将NGR-MOEA与传统多目标进化算法进行比较, 从而验证NGR-MOEA的性能.

3.1 实验设计

3.1.1 测试问题

采用多目标优化测试函数DTLZ[13]作为基础实验比较. 为更突出算法的性能, 本文考虑了DTLZ2,DTLZ4,DTLZ5及DTLZ6 测试问题. 这些测试问题均具有线性、 混合(凸/凹)、 多模型、 脱节、 退化和尺度不一致等特点, 可测试算法的不同性能.

3.1.2 质量测量指标

质量指标是评价算法性能的一个重要指标. 本文实验分别采用反世代距离和空间评测方法两种质量测量指标. 其中, IGD是应用最广泛的指标之一, 可以同时评估算法的收敛性和多样性, 其表示参考点到最近解的距离平均值. IGD值越小, 算法的综合性能越好. IGD值计算公式为

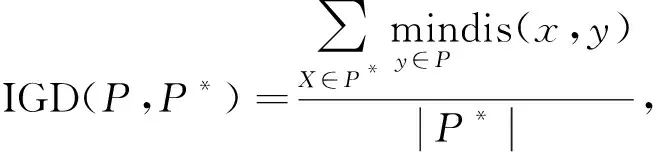
(8)

其中P是算法求得的解集,P*是从PF上采集的一组均匀分布的参考点, dis(x,y)表示参考集P*中的点x到解集P中的点y之间的欧氏距离.

SM描述了解向量的分布, 可衡量PF近似解集中个体在目标空间的分布情况, 并通过与实际Pareto边界的比较度量算法对非支配解的收敛程度. 其所度量的是每个解到其他解最小距离的标准差. 空间度量值越小, 说明解集越均匀. SM计算公式为

(9)

3.2 仿真实验结果

为验证NGR-MOEA在高维多目标优化问题上的求解性能, 将其与NSGA-Ⅱ,GR-MODE和SPEA2这3种目前最具代表性的MOEAs在10,12,15,20目标的DTLZ测试函数集上进行对比实验. 选用可扩展为任意目标维数和自变量维数的通用测试函数DTLZ{2,4,5,6}.

设置种群规模N=100, 迭代次数为250. 为保证实验的公平性和科学性, 对比算法的控制参数设置均采用相应原文献中的推荐值, 且所有实验结果均为各种算法独立运行30次后对应IGD 和SM的统计平均值, 不同算法的对比结果列于表1～表4.

表1 不同算法在DTLZ2中的IGD和SM值对比结果

表2 不同算法在DTLZ4中的IGD和SM值对比结果

由表1～表4可见, NGR-MOEA算法的IGD和SM值在多数情况下优于NSGA-Ⅱ,GR-MODE和SPEA2等算法, 这是因为NGR-MOEA算法在比较个体之间的优劣程度时从优于目标数目和优于幅度两个角度度量, 同时还考虑了每个个体形成的子序列与母序列所形成几何曲线的关联度. 因此, 所获得的最优解集更逼近理论Pareto前沿. 根据DTLZ{2,4,5,6}函数各自功能特性可见： NGR-MOEA在高维多目标优化过程中能获得良好的收敛性能和分布性能, 且随着目标维数增多, GRA-MOEA的性能越好, 表明了NGR-MOEA具有相对较强的稳定性, 适合于高维多目标优化问题的求解.

表3 不同算法在DTLZ5中的IGD和SM值对比结果

表4 不同算法在DTLZ6中的IGD和SM值对比结果

综上所述, 针对传统高维多目标优化问题解决方法存在解集收敛性与解集分布均匀性缺陷的问题, 本文提出了一种新的基于全局排序求解高维多目标优化问题算法, 该算法将个体目标适应度计算策略与灰色关联策略相结合设计新的适应度函数, 从而解决了高维多目标优化问题难以取得良好的收敛性和解集分布性的缺陷. 为验证算法的有效性, 将NGR-MOEA与NSGA-Ⅱ,SPEA2,GR-MODE三种算法进行对比实验, 实验结果表明, NGR-MOEA在10～20 维多目标优化问题上的求解性能具有明显优势, 算法性能得到稳步提高.